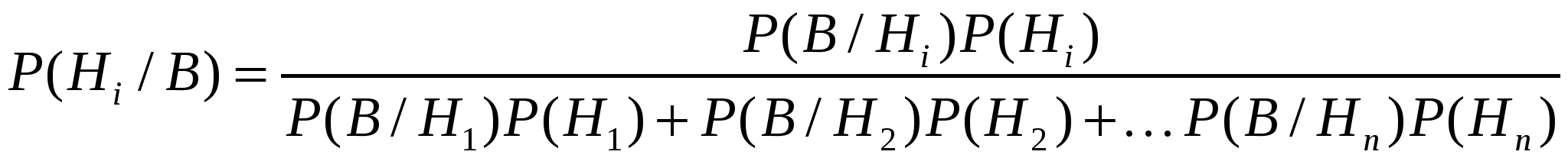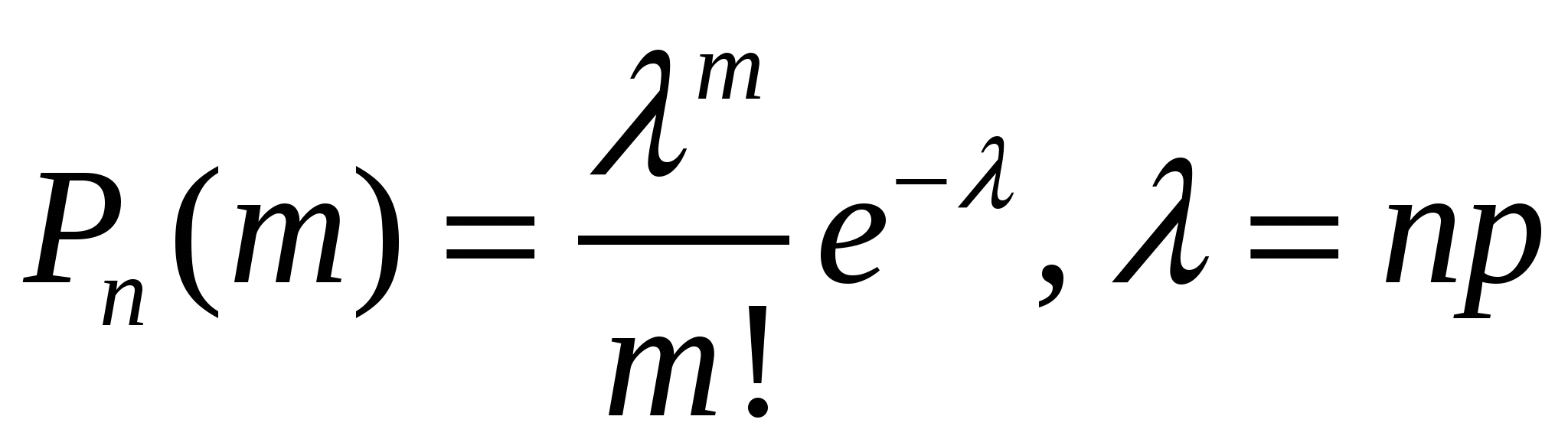В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.
Пусть события А1, А2….. Ап независимы и известны вероятности этих событий:
Р(А1) = р1, Р(Аг) = р2, ..., Р(Ап) = рп.
Обозначив вероятности противоположных событий
Р(А1) = q1 Р(А2) = q2, ..., Р(Ап) = qn,
найдем вероятность того, что ни одно из событий А1, А2, Ап в опыте не наступит:
Р(В) = q1q2… qn.
В этом случае искомая вероятность, т.е. вероятность появления хотя бы одного события, определяется как вероятность противоположного события
Р(В) = 1 - Р(В) = 1- q1q2… qn.
Вероятность преждевременного перегорания электролампы равна 0,1. Какова вероятность того, что из 9 ламп хотя бы одна перегорит преждевременно?
В зоопарке два страуса из 6 имеют рост более 2,5 м. На выездную выставку случайным образом выбирают трех страусов. Какова вероятность того, что среди них хотя бы один с ростом более 2,5 м?
В районе имеется двенадцать заводов, из которых три нерентабельных. На проверку случайным образом отобрано два завода. Найти вероятность того, что среди них:
а) один нерентабельный; б) хотя бы один рентабельный.
Предприятие обеспечивает регулярный выпуск продукции при безотказной поставке комплектующих от двух смежников. Вероятность отказа в поставке продукции от первого из смежников равна 0,05, от второго — 0,08. Найти вероятность сбоя в работе предприятия.
Предположим, что вероятность выловить рыбу при одной поклевке равна 0,7. Какова вероятность того, что рыбак поймает хотя бы одну рыбу, если у него четыре поклевки?
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит хотя бы одну рекламу?
Студент в сессию должен сдать 3 экзамена, причем известно, что положительную оценку он может получить за них с вероятностями 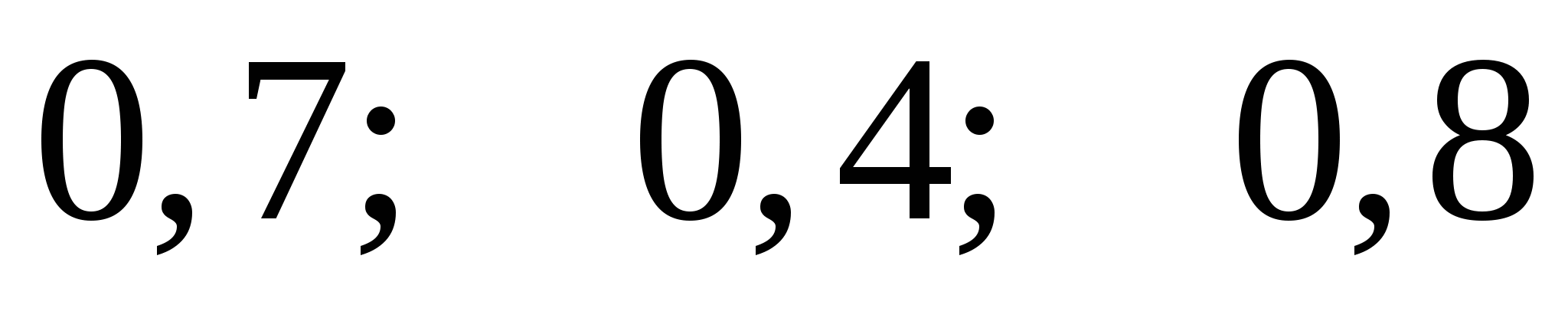 . Предполагая, что различные экзамены представляют собой независимые испытания найти вероятности того, что студент: а) не сдаст ни одного экзамена; б) студент сдаст ровно два экзамена; в) студент сдаст хотя бы один экзамен.
В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества отобрали три шубы случайным образом. Определить вероятность того, что среди отобранных шуб окажутся:
а) только женские шубы;
б) только мужские или только женские шубы.
На предприятие поступают заявки от нескольких торговых пунктов. Вероятности поступления заявок от пунктов А и В равны соответственно 0,5 и 0,4. Найти вероятность поступления заявок от пункта А или от пункта В, считая события поступления заявок от этих пунктов независимыми, но совместными.
Вероятности своевременного выполнения задания тремя независимо работающими предприятиями соответственно равны 0,5; 0,6; 0,7. Найти вероятность своевременного выполнения задания хотя бы одним предприятием.
Три стрелка производят по одному выстрелу в мишень. Вероятность попадания в цель для первого стрелка равна 0,6; 0,7 для второго и 0,5 для третьего. Найти вероятность того, что цель будет поражена.
Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что наступит банкротство хотя бы одной компании?
Вероятность получить высокие дивиденды по акциям на первом предприятии - 0.1, на втором - 0.2, на третьем – 0.25. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.
В магазине выставлены для продажи 20 изделий, среди которых 4 изделий некачественных. Какова вероятность того, что взятые случайным образом 3 изделия будут:
а) качественными;
б) хотя бы один из них будет качественным;
в) ни одного качественного изделия.
Формула полной вероятности и формула Байеса
Если некоторое событие В совершается с одним из п несовместрых событий 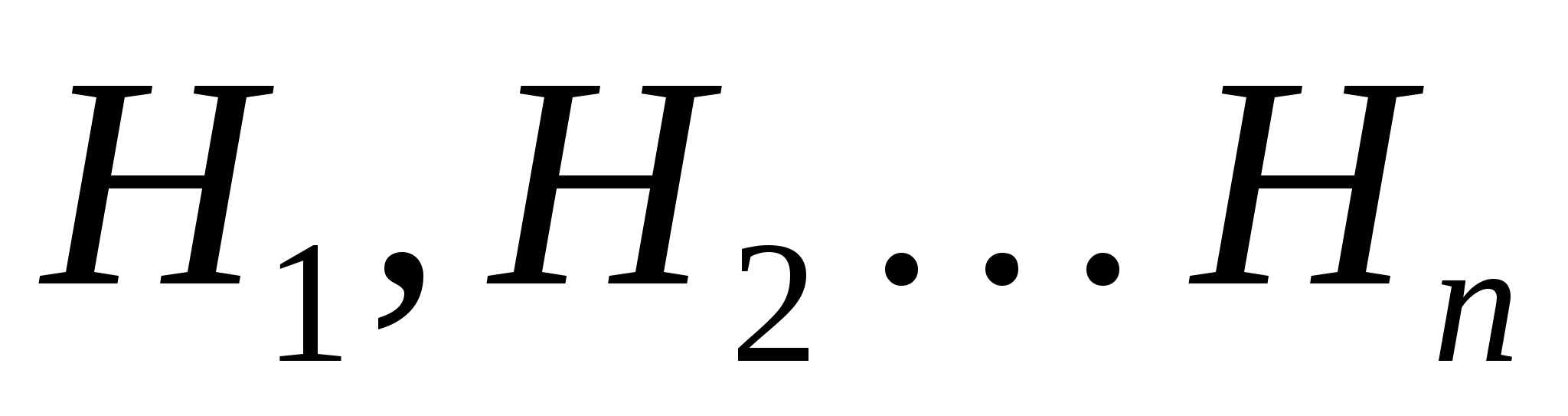 , образующих полную группу событий, то для определения вероятности этого события может быть использована формула полкой вероятности
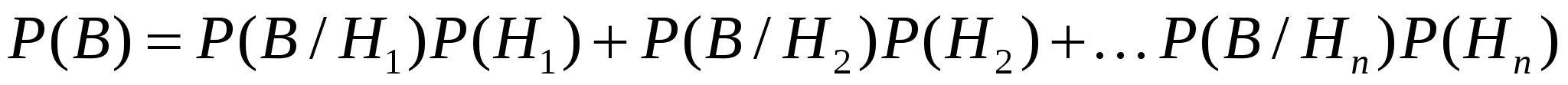
Для определения вероятности события 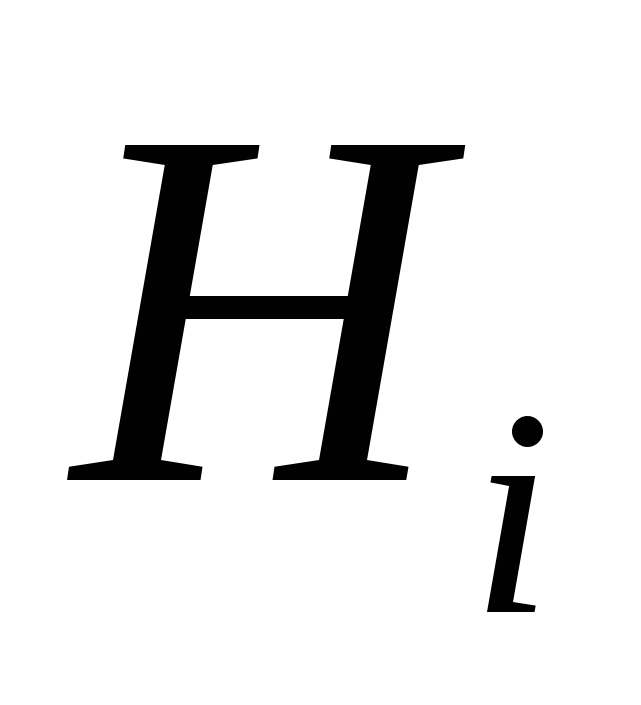 при условии, что произошло событие В, используется формула Байеса
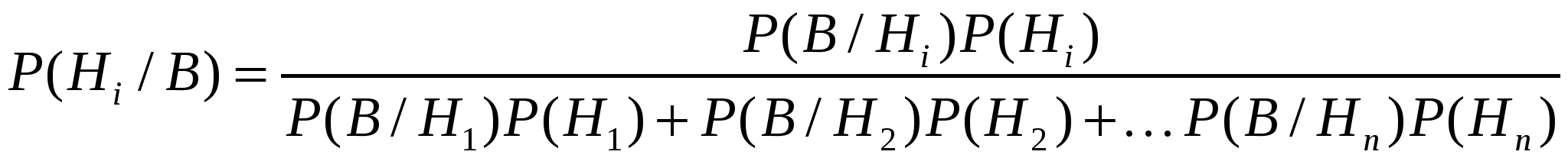
На автозавод поступили двигатели от трех моторных заводов. От первого завода поступило 10 двигателей, от второго — б и от третьего — 4 двигателя. Вероятности безотказной работы этих двигателей в течение гарантийного срока соответственно равны 0,9; 0,8; 0,7.
Какова вероятность того, что:
а) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока;
б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе?
Вероятности своевременного выполнения задания тремя независимо работающими предприятиями соответственно равны 0,5; 0,6; 0,7. Найти вероятность своевременного выполнения задания хотя бы одним предприятием.
В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Найти вероятность того, что
а) приобретенное изделие окажется нестандартным
б) приобретенное изделие оказалось стандартным
в) приобретенное изделие оказалось стандартным. Какова вероятность того, что оно изготовлено третьей фирмой?
Г) приобретенное изделие оказалось нестандартным. Какова вероятность того, что оно изготовлено третьей фирмой?
Д) Приобретенное изделие оказалось стандартным. Какова вероятность того, что оно изготовлено второй фирмой?
На предприятии, изготавливающем замки, первый цех производит 25, второй 35, третий 40% всех замков. Брак составляет соответственно 5, 4 и 2%.
а) Найти вероятность того, что случайно выбранный замок является дефектным.
б) Случайно выбранный замок является дефектным. Какова вероятность того, что он был изготовлен в первом, втором, третьем цехе?
Трое рабочих изготавливают однотипные изделия. Первый рабочий изготовил 40 изделий, второй — 35, третий — 25. Вероятность брака у первого рабочего 0,03, у второго — 0,02, у третьего — 0,01. Взятое наугад изделие оказалось бракованным. Определить вероятность того, что это изделие сделал второй рабочий.
В данный район изделия поставляются тремя фирмами в соотношении 5:8:7. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%, третьей – 75%. Приобретенное изделие оказалось стандартным. Найти вероятность того, что оно поставлено второй фирмой.
На предприятии работают две бригады рабочих: первая производит в среднем 3/4 продукции с процентом брака 4%, вторая — х/4 продукции с процентом брака 6?/о. Найти вероятность того, что взятое наугад изделие:
а) окажется бракованным;
б) изготовлено второй бригадой при условии, что изделие оказалось бракованным.
В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель — 0,85. Проведена проверка качества одной пары обуви. Оказалось, что эта пара обуви отремонтирована качественно. Какова вероятность того, что это а) сапоги, б) туфли?
В группе 4 отличника, 10 хорошо успевающих и 6 занимающихся слабо студентов. На предстоящем экзамене отличники могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. На экзамен наугад приглашается один студент. Какова вероятность того, что он получит хорошую оценку?
В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель 0,85. Какова вероятность того, что отобранная для проверки пара отремонтирована качественно?
На сборку поступают детали с двух автоматов. Первый дает в среднем 2% брака, второй 3% брака. Найти вероятность того, что наугад взятая бракованная деталь изготовлена вторым автоматом, если с первого автомата поступило 1000 деталей, а со второго 2000.
Известно, что 90% выпускаемой продукции соответствует стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,9 и нестандартную с вероятностью 0,2. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
В магазин бытовой техники поступила партия холодильников трех торговых марок: «Дед Мороз», «Снегурочка» и «Северный олень». В поступившей партии 10% холодильников «Дед Мороз», 40% холодильников «Снегурочка», остальные – «Северный олень». Известно, что холодильники данных торговых марок не требуют ремонта в течение гарантийного срока, соответственно, в 98%, 88% и 92% случаях.
А) Найти вероятность того, что случайно выбранный из партии холодильник не потребует ремонта в течение гарантийного срока.
Б) Случайно выбранный холодильник сломался в течение гарантийного срока. Какова вероятность того, что это холодильник марки «Снегурочка»
Аналитик, занимающийся прогнозом котировок акций компании, ожидает роста стоимости акций с вероятностью 0.85, при условии, что экономика страны будет находиться в состоянии подъема. По его оценкам, в случае экономического спада, вероятность роста котировок акции компании снижается до 0.40. Согласно предварительным прогнозам вероятность экономического подъема в стране в следующем году оценивается на уровне 65%. Перед аналитиком поставлена задача: дать оценку вероятности роста цен на акции компании в новом году. Каков Ваш прогноз?
Сотрудник консалтингового агентства проводит анализ тенденций на валютном рынке с целью расчета доходности будущих инвестиций. Согласно предварительному прогнозу, укрепление доллара США в период активного экономического роста ожидается с вероятностью 0.75; в период умеренного экономического роста с вероятностью 0.45 и в период стагнации с вероятностью 0.25. Кроме того, есть основания полагать, что активный экономический рост будет происходить с вероятностью 0.25, умеренный экономический рост с вероятностью 0.35 и будет наблюдаться стагнация с вероятностью 0.40.
А) Какова вероятность того, что в прогнозируемый период произойдет укрепление доллара?
Б) Известно, что в прогнозируемый период произошло укрепление доллара. Какова вероятность того, что этот период ознаменован высокими темпами экономического роста
В район изделия поставляются тремя фирмами. Известно, что первая фирма поставляет товар с браком в 0,1%, вторая – 0,15%, третья – 0,25%. С первой фирмы поступило 500, со второй – 200, а с третьей – 300 изделий. Найти вероятность, что приобретённое изделие окажется
а) стандартным;
б) нестандартным;
в) какова вероятность, что стандартное изделие поступило с третьей фирмы?
Формулы Бернулли и Пуассона
Если при проведении испытаний вероятность появления события А не зависит от исходов других испытаний, то такие испытания называются независимыми.
Формула Бернулли определяет вероятность появления ровно т раз события А в серии из п независимых испытаний, в каждом из которых вероятность появления события А равна р:
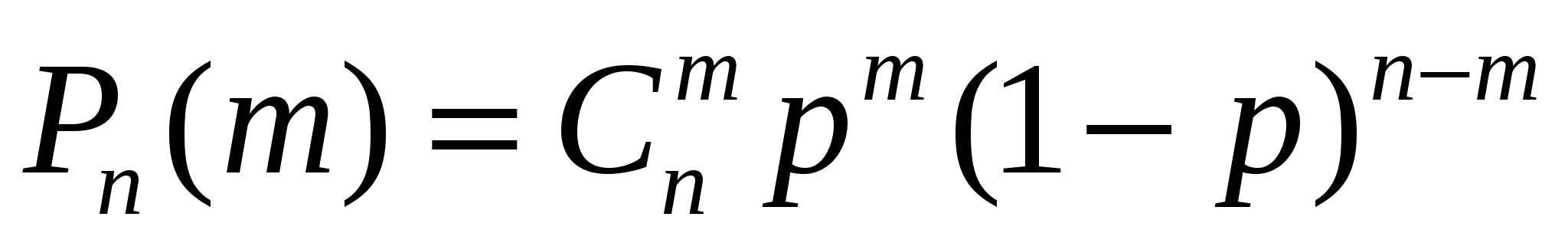
В ряде случаев требуется определить вероятности появления события А менее т раз (X < т), более т раз (X > т), не менее т раз (X > т), не более т раз (X < т). В этих случаях могут быть использованы формулы
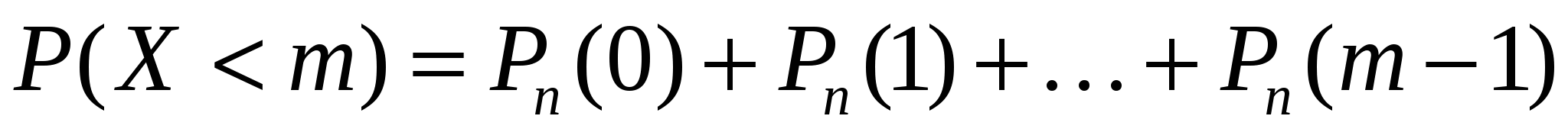
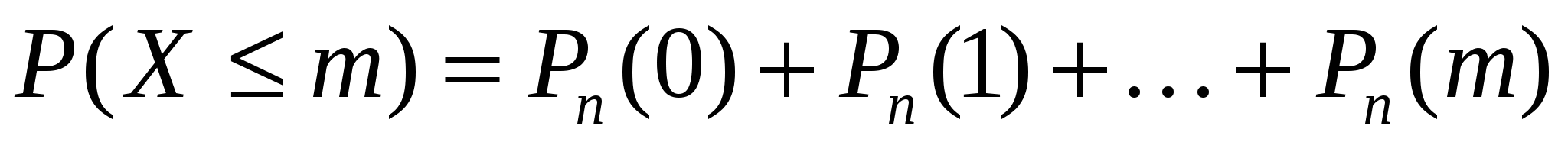
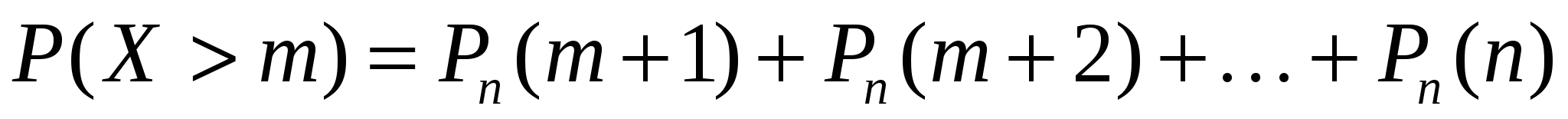
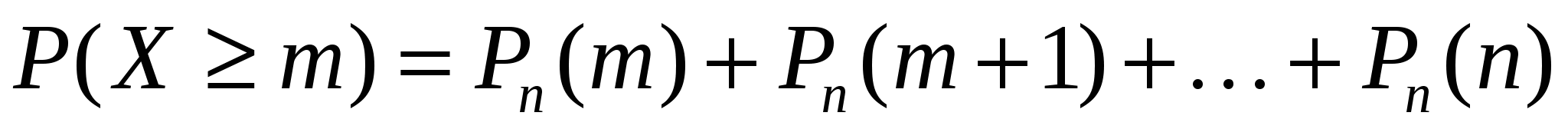
При больших п и малых р вычисления по формуле Бернулли затруднены. В этих случаях обычно используется формула Пуассона
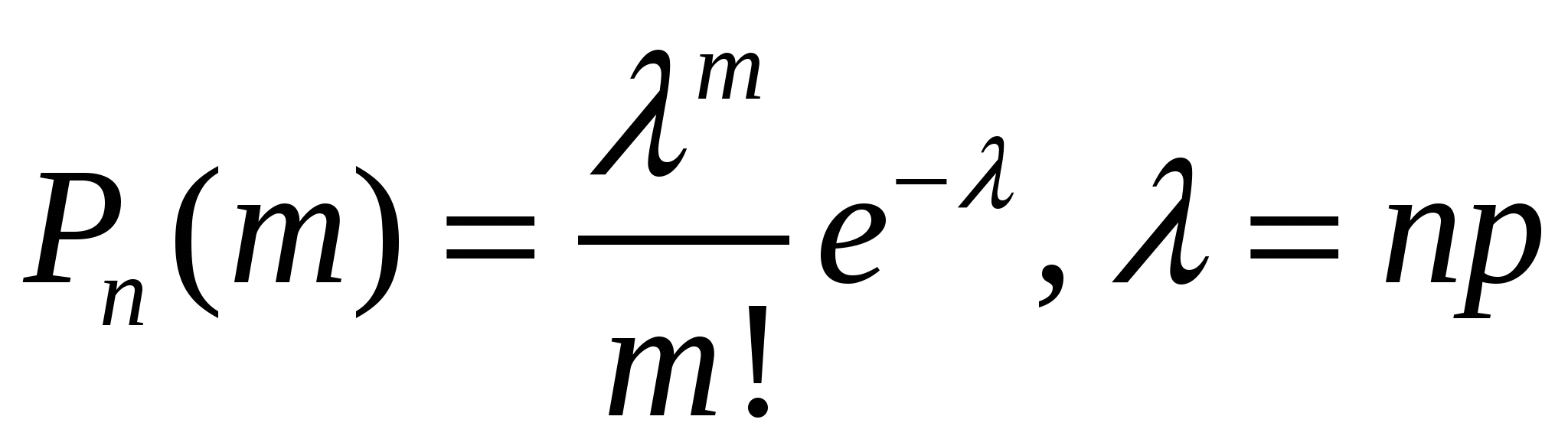
В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:
а) одного мальчика;
б) двух мальчиков.
Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки «А», равна 0,4. Найти вероятность того, что холодильник потребуется:
а) не менее чем двум покупателям;
б) не более чем трем покупателям;
в) всем четырем покупателям.
Работают четыре магазина по продаже стиральных машин. Вероятность отказа покупателю в магазинах равна 0,1. Считая, что ассортимент товара в каждом магазине формируется независимо от других, определить вероятность того, что покупатель получит отказ в двух, в трех и в четырех магазинах.
Каждый из пяти лифтов в высотном доме в течение месяца работает нормально с вероятностью 0,9. Найти вероятность того, что в течение месяца будут работать нормально:
а) 3 лифта; б) более 3 лифтов.
Студент приобрел пять лотерейных билетов. Вероятность выигрыша по одному билету составляет 0,2. Найти вероятность того, что студент выиграет:
а) по трем лотерейным билетам;
б) не менее чем по трем билетам;
в) хотя бы по одному билету.
г) Определить наивероятнейшее число выигрышных билетов.
В среднем по 15 % договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая будет связано с выплатой страховой суммы:
а) три договора;
б) менее двух договоров.
В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут два, три и пять замков.
Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что при транспортировке будет повреждено:
а) ровно три изделия;
б) более трех изделий.
На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа из строя выйдут два, три и пять автоматов?
Вероятность выпуска бракованной микросхемы равна 0,002. Какова вероятность того, что из 2000 присланных в магазин микросхем окажется не менее 3 бракованных?
Всхожесть семян огурцов равна 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?
Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено а) ровно 4 пары, б) ровно 5 пар.
Завод производит мобильные телефоны. Вероятность того, что выпущенный телефон бракованный, равна 0,015. Найти вероятность того, что в партии из 200 телефонов окажется хотя бы один бракованный.
Вероятность повреждения бутылки с минеральной водой при перевозке равна 0,002. Найти вероятность того, что из 2000 бутылок при перевозке будет повреждено менее двух.
Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет:
а) на пяти веретенах;
б) хотя бы на двух веретенах
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Закон распределения вероятностей
|
Скачать 0.55 Mb.