|
|
тервер практикум. Классическое определение вероятности события
Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется такая, значения которой есть конечное или счетное множество фиксированных величин. Для описания поведения дискретной случайной величины X задают все значения х1, хг, ..., хп, которые она может принять, и вероятности появления этих значений р1 р2, рп.
Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причем
Р1 +р2 +рп=1
Ряд распределения можно задать графически, откладывая на горизонтальной оси значения X, а на вертикальной — соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.
Задачи
Среди 10 лотерейных билетов имеется 4 билета с выигрышем. Наудачу покупают 2 билета. Написать закон распределения вероятностей числа выигрышных билетов среди купленных.
В партии из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон распределения числа дефектных курток среди купленных. Построить многоугольник распределения.
Из партии в 20 изделий, среди которых имеется 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа X бракованных изделий среди отобранных.
В коробке 20 одинаковых катушек ниток, из них — 4 катушки с белыми нитками. Наудачу вынимают 2 катушки. Найти закон распределения числа катушек с белыми нитками среди вынутых.
В урне имеются 3 белых и 3 синих шара. Одновременно вынимаются три шара. Составить закон распределения случайной величины X, которая равна числу синих шаров среди вынутых.
Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попаданий мяча в корзину.
В урне 2 красных и 3 зеленых шара. Из урны извлекают шары до тех пор, пока не появится зеленый. Пусть случайная величина Xравна числу извлеченных шаров. Найти закон распределения X.
Партия содержит 20 телевизоров, среди которых 6 с дефектом. Купили два телевизора. Составить ряд распределения исправных телевизоров среди купленных.
Три баскетболиста один за другим бросают мяч в корзину. Вероятности попадания для первого, второго и третьего баскетболистов равны соответственно 0,7, 0,8, и 0,9. Составить закон распределения числа попаданий.
Студент в сессию должен сдать 3 экзамена, причем известно, что положительную оценку он может получить за них с вероятностями 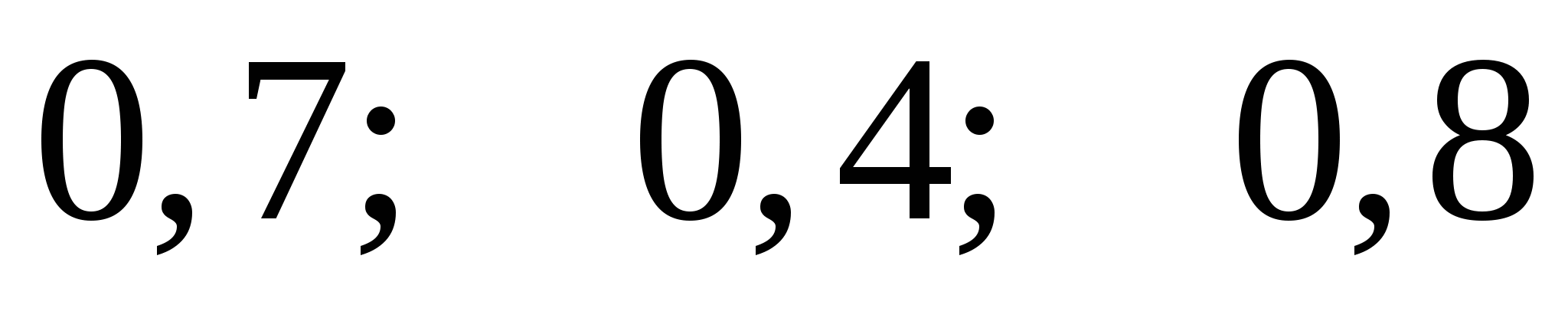 . Предполагая, что различные экзамены представляют собой независимые испытания, построить ряд распределения и многоугольник распределения случайной величины . Предполагая, что различные экзамены представляют собой независимые испытания, построить ряд распределения и многоугольник распределения случайной величины 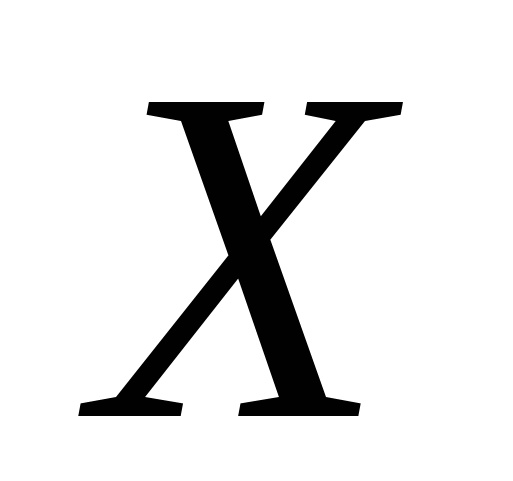 – числа успешно сданных экзаменов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение – числа успешно сданных экзаменов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение 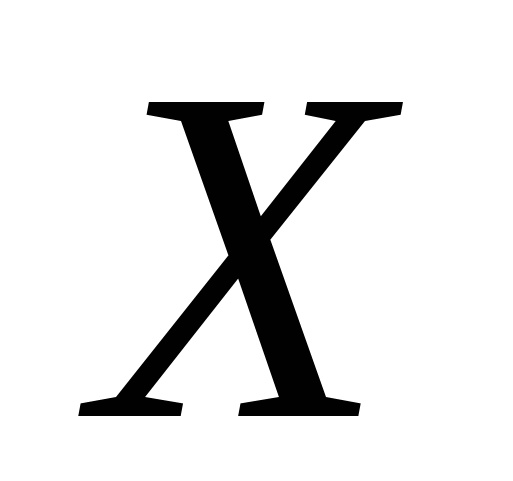 . Найти вероятности того, что студент: а) не сдаст ни одного экзамена; б) студент сдаст ровно два экзамена; в) студент сдаст хотя бы один экзамен. . Найти вероятности того, что студент: а) не сдаст ни одного экзамена; б) студент сдаст ровно два экзамена; в) студент сдаст хотя бы один экзамен.
Имеются три базы с независимым снабжением. Вероятность отсутствия на базе нужного товара равна 0,1. Предприниматель решил закупить некий товар. Составить закон распределения числа баз, на которых в данный момент этот товар отсутствует.
Бросают три игральных кубика. Составить закон распределения числа выпавших «шестерок» на трех кубиках. Построить многоугольник распределения.
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента 0,15. Составить закон распределения отказавших элементов.
Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3. Аудитору на заключение представлено 3 баланса предприятия. Составить закон распределения числа положительных заключений на проверяемые балансы.
Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса, равна 0,05. Аудитору на заключение представлено 2 баланса. Составить закон распределения числа правильных заключений на проверяемые балансы.
Вероятность сбоя в работе АТС равна 0,1. Составить закон распределения числа сбоев, если в данный момент поступило 5 вызовов.
Имеется 4 различных ключа, из которых только один подходит к замку. Составить закон распределения числа опробованных ключей, если опробованный ключ в дальнейшем не участвует в испытаниях.
В магазин привезли арбузы из Ташкента и Камышина в равных количествах. Вероятность покупки неспелого арбуза равна соответственно 0,1 и 0,3. Куплено 4 арбуза. Составить закон распределения спелых арбузов среди купленных.
У продавца имеются изделия, полученные в равных количествах с трех фабрик. Вероятность того, что эти изделия отличного качества, для каждой фабрики соответственно составляет 0,8; 0,7 и 0,9. Отобрано 2 изделия. Составить закон распределения количества изделий отличного качества среди отобранных.
Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель, равна 0,8, а вероятность того, что второй — 0,6. Случайная величина X — число покупок, сделанных покупателями. Описать закон распределения случайной величины X.
В лотерее из 100 билетов разыгрываются два выигрыша на сумму 200 руб. и 60 руб. Стоимость билета 10 руб. Составить закон распределения суммы чистого выигрыша для лица, купившего два билета.
В лотерее 100 билетов, из которых 2 выигрышных по 50 руб. и 10 выигрышных по 1 руб. Стоимость билета 2 руб. Составить закон распределения суммы чистого выигрыша для лица, купившего 2 билета. Построить многоугольник распределения.
Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупательь, равна 0,6, а вероятность того, что второй — 0,8. величина X — число покупок, сделанных покупателями. Найти закон распределения X.
Среди 7 купленных театральных билетов 3 билета в партер. Наудачу взяли 4 билета. Составить закон распределения случайной величины, равной числу билетов в партер среди взятых. Найти математическое ожидание и дисперсию этой случайной величины.
В экзаменационном билете три задачи. Вероятность того, что студент правильно решит первую задачу, равна 0,9, вторую – 0,8, третью – 0,7.
1. Составить закон распределения случайной величины – числа правильно решенных задач в билете.
2. Построить полигон распределения.2.
3. Найти вероятность того, что случайная величина примет значение:
а) в промежутке ; [1; 3)
б) не менее чем 0,5;
в) в промежутке [1,5; 3],
Ряд распределения случайной величины X имеет вид
X
|
-5
|
2
|
3
|
4
|
p
|
0,3
|
C
|
0,5
|
0,1
|
Вычислить
1)C
2) 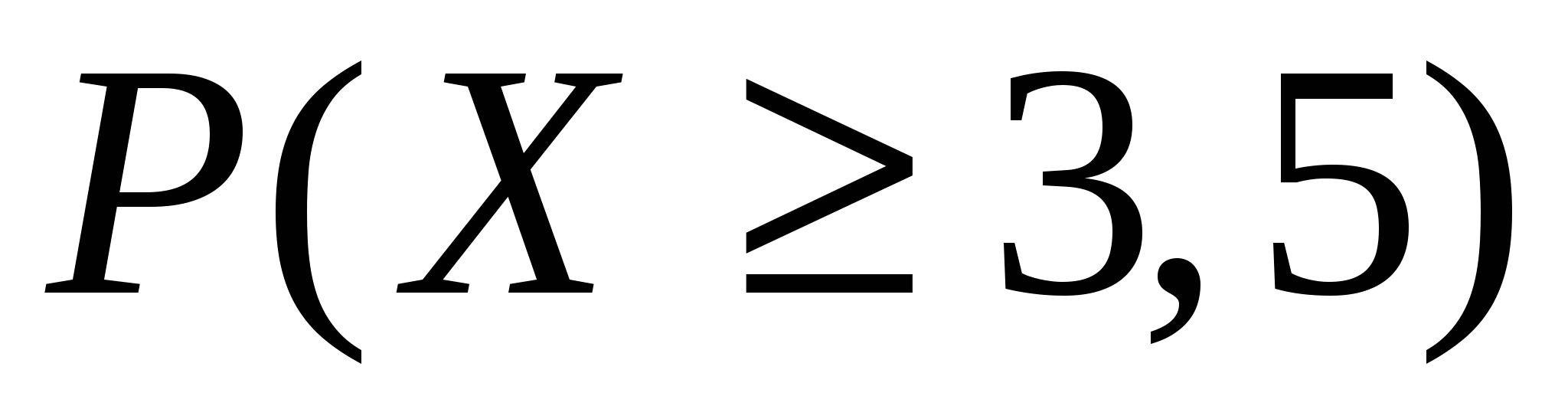
3) Р(|Х| < 2,5).
Ряд распределения случайной величины X имеет вид
X
|
0
|
2
|
4
|
5
|
p
|
0,3
|
0,05
|
0,5
|
C
|
Вычислить
1)C
2) 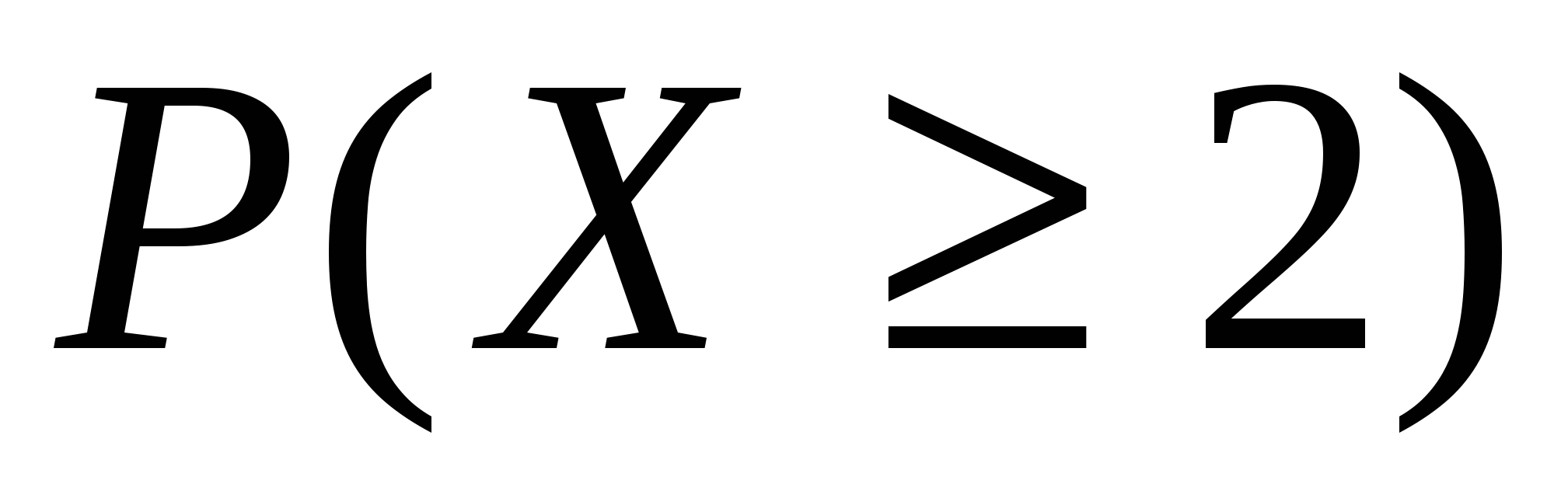
3) Р(Х <4).
Математическое ожидание и дисперсия
Математическим ожиданием дискретной случайной величины называется сумма вида
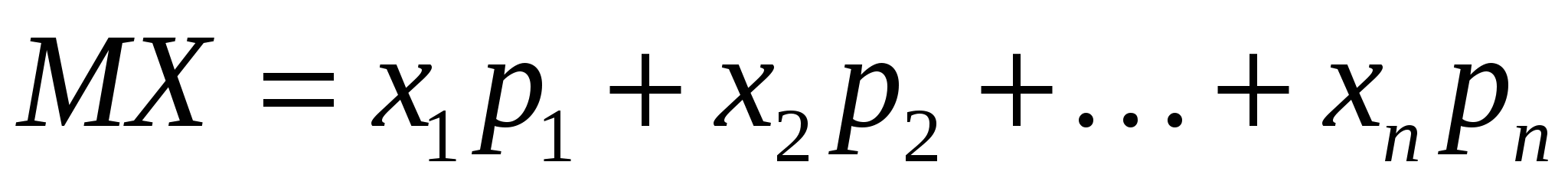
Свойства математического ожидания:
M(CX)= СМ(Х); М(С) = С, где С-произвольная постоянная величина.
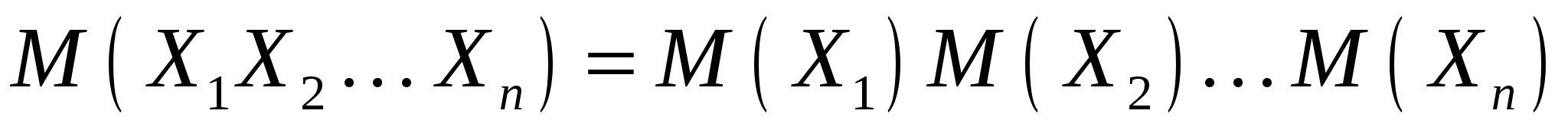 , если , если 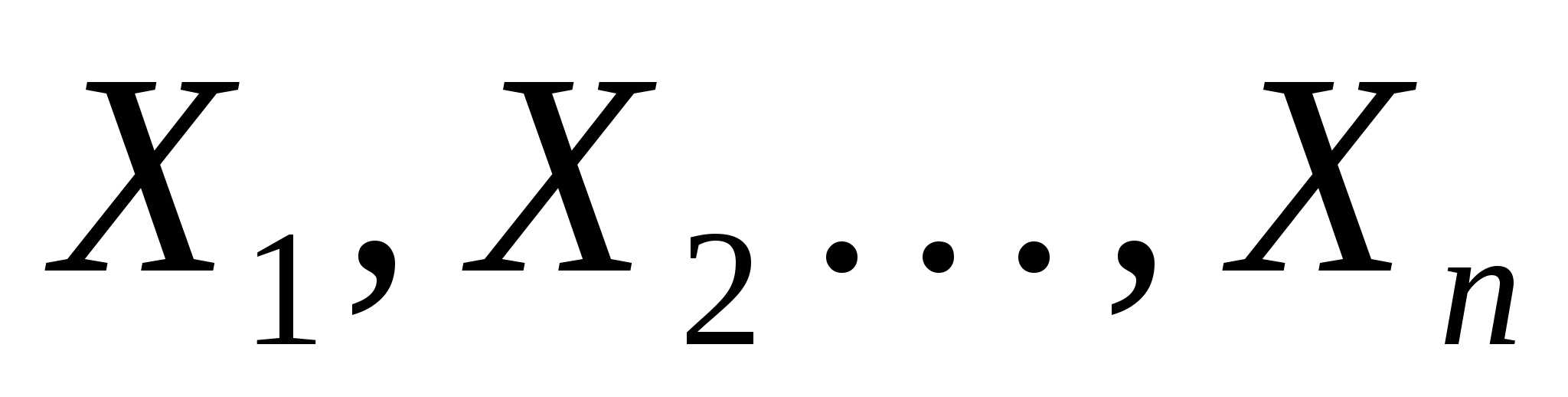 - -
взаимно независимые случайные величины.
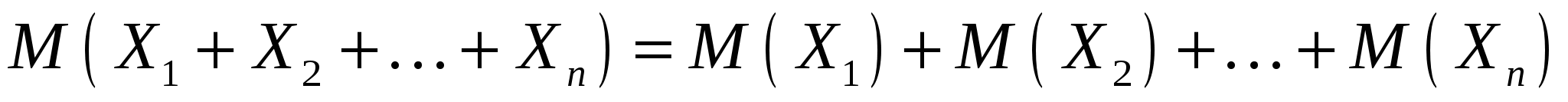 . .
Математическое ожидание характеризует среднее значение случайной величины.
Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратичное отклонение.
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = М(Х - М(Х))2.
Дисперсию целесообразно вычислять по формуле
D(X) = М(Х2) - (М(Х))2.
Свойства дисперсии:
D(CX)= С2D(Х); D(С) = 0, где С-произвольная постоянная величина.
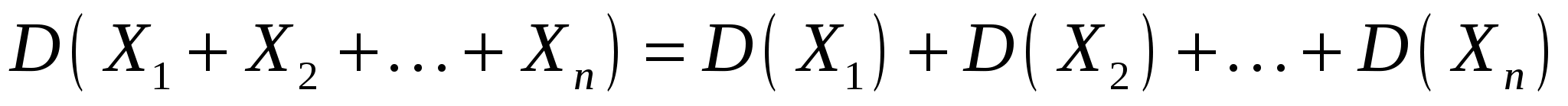 , если , если 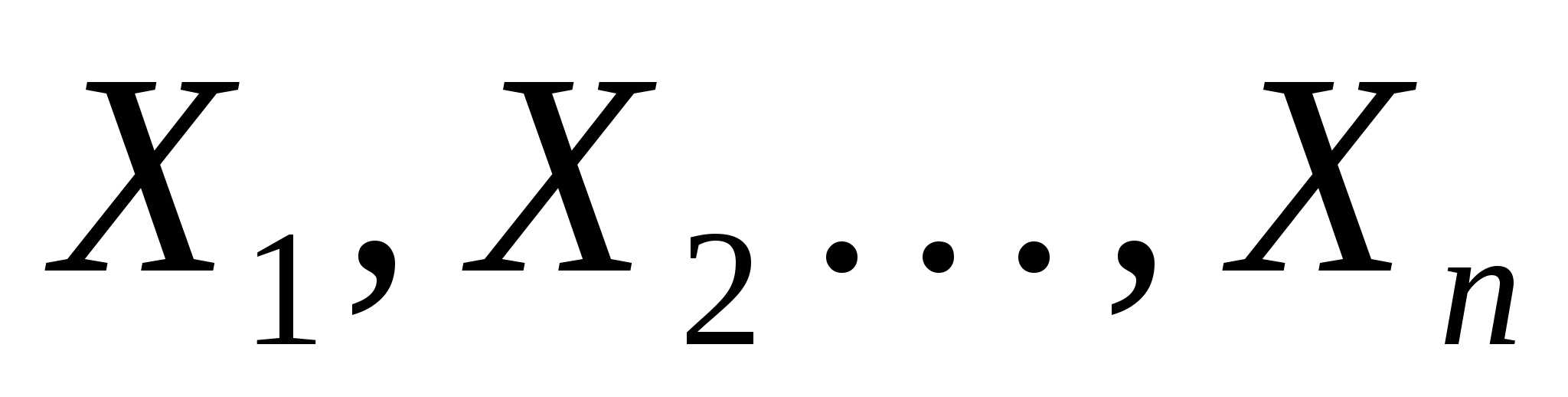 - взаимно независимые случайные величины. - взаимно независимые случайные величины.
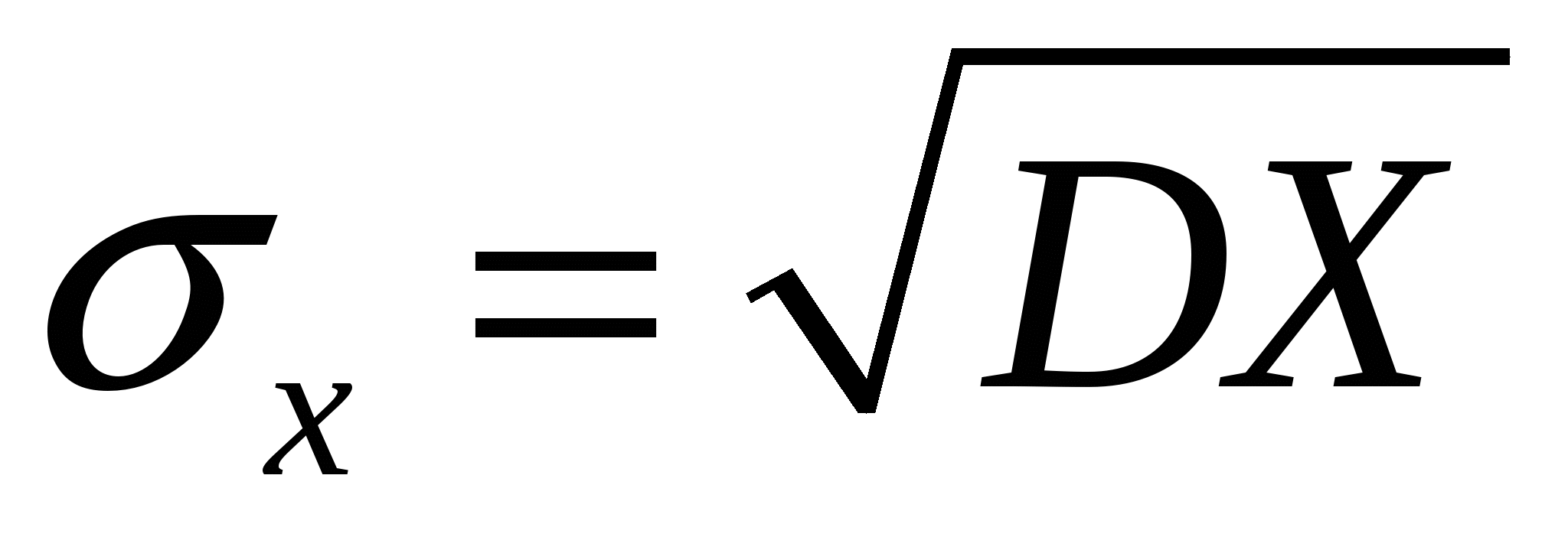 - среднеквадратичное отклонение - среднеквадратичное отклонение
Даны законы распределения двух независимых случайных величин:
X
|
2
|
4
|
6
|
8
|
P
|
0,4
|
0,2
|
0,1
|
0,3
|
Найти
MX, MY
DX, DY
MZ, DZ, где Z = 2Х + ЗY
Задан ряд распределения:
X
|
2
|
3
|
5
|
6
|
7
|
10
|
P
|
0,4
|
0,2
|
0,2
|
0,05
|
0,1
|
0,05
|
Найти М(Х), D(Х) и М(2Х2 + 3).
Даны законы распределения независимых случайньх независимых величин:
Найти M(Z) и D(Z), если Z = (X + У)/2.
В экзаменационном билете три задачи. Вероятность того, что студент правильно решит первую задачу, равна 0,9, вторую – 0,8, третью – 0,7. Пусть X – число правильно решенных задач. Определить числовые характеристики случайной величины: математическое ожидание, дисперсию и среднее квадратическое отклонение.
С целью привлечения покупателей компания «Кока-кола» проводит конкурс, согласно которому каждая десятая бутылка напитка, выпущенная фирмой, является призовой. Составить закон распределения числа призовых из четырех приобретенных покупателем бутылок. Найти математическое ожидание и дисперсию этой случайной величины.
В партии из 8 деталей 6 деталей – стандартные. Наугад отбираются две детали.Составить закон распределения случайной величины, равной числу стандартных деталей среди отобранных. Найти ее математическое ожидание, дисперсию.
Вероятность наличия нужной книги для первой библиотеки равна 0,2; для второй, третьей и четвертой соответственно 0,2, 0,4 и 0,5. Составить закон распределения числа библиотек, которые последовательно посещает студент в поисках нужной книги. Найти математическое ожидание и дисперсию этой случайной величины.
Ткачиха обслуживает 3 станка. Вероятности того, что в течение часа станок не потребует внимания, равны соответственно 0,9; 0,8; 0,7. Составить закон распределения для числа станков, потребовавших внимания в течение часа. Найти математическое ожидание и дисперсию этой случайной величины.
Молодого человека пригласили на день рождения. Он помнил номер дома, но забыл номер квартиры, помня лишь, что номер однозначный и нечетный. Составить закон распределения числа посещенных квартир для отыскания нужной. Найти математическое ожидание и дисперсию этой случайной величины.
Устройство состоит из трех независимо работающих приборов. Вероятности отказа приборов 0,3; 0,64; 0,5.Cоставить закон распределения числа отказавших приборов. Найти математическое ожидание и дисперсию.
Фирма имеет 4 грузовых автомобиля. Вероятность выхода на линию каждого автомобиля равна 0,8. Составить закон распределения случайной величины, равной числу автомобилей, которые выйдут на линию в произвольно выбранный день. Найти математическое ожидание и дисперсию этой случайной величины.
Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее при первом выстреле равна 0,8, а для каждого последующего выстрела уменьшается на 0,1.Составить закон распределения случайной величины, равной числу попаданий в цель. Найти математическое ожидание и дисперсию этой случайной величины.
Вероятность выигрыша по одному билету лотереи равна 0,05. Найти математическое ожидание M(2X-0,5), если случайная величина Xравна числу выигрышных билетов среди 15 купленных.
Ветеринар в зоопарке обследует 5 жирафов. Вероятность того, что рост жирафа будет больше 6 метров, равна 0,1. Найти дисперсию D(2X+ 4), если случайная величина Xравна числу обследованных жирафов с ростом более 6 метров.
Два консервных завода поставляют продукцию в магазин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90%, а на втором — 80%. В магазине куплено 3 банки консервов. Найти математическое ожидание и среднее квадратичное отклонение числа банок с продукцией высшего качества.
Два товароведа проверяют партию изделий. Производительность их труда соотносится как 5:4. Вероятность определения брака первым товароведом составляет 85%, вторым — 90%. Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б) дисперсию числа годных изделий среди отобранных.
В магазин поступили электролампы с трех заводов в пропорции 2:3:5. Доля брака в продукции первого завода — 5%, второго — 2%, третьего — 3%. Покупатель приобрел 3 лампочки. Найти а) математическое ожидание и б) среднее квадратичное отклонение числа качественных лампочек среди купленных.
Стороны прямоугольного участка X и У в результате погрешностей измерения оказываются случайными величинами с такими распределениями:
X
|
19,5
|
19,7
|
20
|
20,2
|
P
|
0,2
|
0,05
|
0,7
|
0,05
|
Y
|
29,5
|
29,8
|
30
|
30,1
|
P
|
0,15
|
0,15
|
0,65
|
0,05
|
Найти математическое ожидание площади участка, если известно, что измерения проводились независимыми способами.
ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
На отрезок [0;1] наудачу бросается голодная точка. Какова вероятность того, что она попадёт в промежуток [0,4;0,7]?
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина большего отрезанного куска составит не менее 80 см.
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
В квадрат вписан равнобедренный треугольник так, что его основание совпадает со стороной квадрата. В квадрат случайным образом бросается точка. Найти вероятность того, что точка не попадет в треугольник.
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.
В прямоугольнике 5*4 см2 находится круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
В квадрат со стороной 2 м брошена точка. Найти вероятность того, что точка будет удалена от центра квадрата не больше чем на 0,5 м.
В квадрат с вершинами наудачу брошена точка . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству.
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Функция распределения вероятностей, и плотность вероятности
|
|
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb.