Комбинаторные методы решения вероятностных задач. ДЗ 1. Решение. Пусть событие а получение слова крот
 Скачать 42.8 Kb. Скачать 42.8 Kb.
|
|
Комбинаторные методы решения вероятностных задач №1. На четырех карточках написаны буквы o, т, к, р. Карточки перевернули и перемешали. Затем открыли наугад последовательно одну за другой эти карточки и положили в ряд. Какая вероятность того, что получится слово «крот»? Решение. Пусть событие А – получение слова «крот». 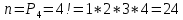 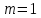 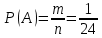 Ответ: 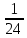 №2. Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые четыре цифры, которые знал, и наугад комбинацию из цифр 1, 5 и 9. Какова вероятность того, что абонент набрал верный номер? Решение. Пусть событие А – набор верного номера. 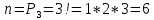 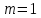 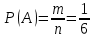 Ответ: 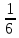 №3. Взяли четыре карточки. На первой написали букву о, на второй т, на третьей с, на четвертой п. Карточки перевернули и перемешали. Затем открыли наугад одну карточку за другой и положили рядом. Какова вероятность того, что в результате получится слово «стоп» или слово «пост»? Решение. Пусть событие А – получение слова «стоп» или «пост». 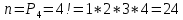 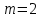 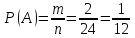 Ответ: 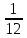 №4. На каждой из двух карточек написана цифра 1, а на третьей – цифра 2. Эти карточки перемешиваются и случайным образом выкладываются в ряд. Какова вероятность того, что образовалось число: 1) 112; 2) 121. 1) Решение. Пусть событие А – получение 112. 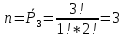 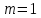 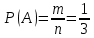 2) Решение. Пусть событие А – получение 121. 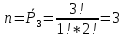 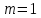 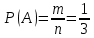 Ответ: 1) 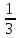 ; 2) ; 2) 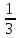 №5. Чтобы открыть сейф, надо набрать в определенной последовательности пять (без их повторения): 1, 2, 3, 4 и 5. Какова вероятность того, что если набирать цифры в произвольном порядке, то сейф откроется? Решение. Пусть событие А – открытие сейфа.    Ответ:  №6. 4 одинаковых шара пронумерованы числами 1, 2, 3, 4 и сложены в ящик. Случайным образом из ящика извлекают по одному шару. Какова вероятность того, что шары были извлечены в последовательности: 1) 4, 2, 1, 3; 2) 4, 3, 2, 1. 1) Решение. Пусть событие А – извлечение шаров в правильной последовательности    2) Решение. Пусть событие А – извлечение шаров в правильной последовательности    Ответ: 1)  ; 2) ; 2)  №7. На трех карточках написаны цифры 1, 2 и 3 (на каждой карточке по одной цифре). Случайным образом из этого набора выбирают последовательно по одной карточке и кладут в ряд, образуя трехзначное число. Какова вероятность того, что образуется число: 1)  ; 2) ; 2)  . . 1) Решение. Пусть событие А – получение нужного числа    2) Решение. Пусть событие А – получение нужного числа    Ответ: 1)  ; 2) ; 2)  №8. На карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад последовательно одну за другой эти карточки, расположив их в ряд слева направо. Какова вероятность того, что в результате получилось: А) число 123; Б) число 312 или 321; В) число первая цифра которого 2. А) Решение. Пусть событие А – получение нужного числа   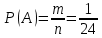 Б) Решение. Пусть событие А – получение нужного числа 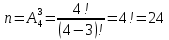 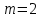 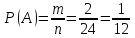 В) Решение. Пусть событие А – получение нужного числа 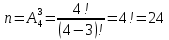 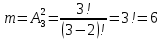 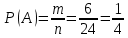 Ответ: а) 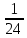 ; б) ; б) 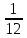 ; в) ; в) 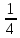 №9. На каждой карточке написана одна из букв о, п, р, с, т. Несколько карточек наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании: А) 3 карточек получится слово рот; Б) 4 карточек получится слово сорт; В) 5 карточек получится слово спорт. А) Решение. Пусть событие А – получение слова рот 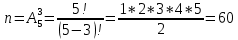 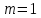  Б) Решение. Пусть событие А – получение слова сорт    В) Решение. Пусть событие А – получение слова спорт    Ответ: а)  ; б) ; б)  ; в) ; в)  №10. В клетки квадратной таблицы  произвольно ставят крестики и нолики. Найдите вероятность того, что: А) будет поставлен ровно один крестик; Б) Будут поставлены ровно два нолика; В) в левой нижней клетке будет стоять крестик; Г) в верхней левой и нижней правой клетках будут разные значки. произвольно ставят крестики и нолики. Найдите вероятность того, что: А) будет поставлен ровно один крестик; Б) Будут поставлены ровно два нолика; В) в левой нижней клетке будет стоять крестик; Г) в верхней левой и нижней правой клетках будут разные значки. А) Решение. Пусть событие А – когда поставлен один крестик    Б) Решение. Пусть событие А – когда поставлены два нолика   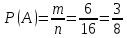 В) Решение. Пусть событие А – когда в левой нижней клетке будет стоять крестик 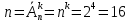 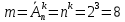 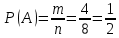 Г) Решение. Пусть событие А – когда в верхней левой и нижней правой клетках будут разные значки    Ответ: а)  ; б) ; б) 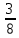 ; в) ; в) 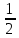 ; г) ; г) 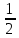 №11. На бильярдном столе – шары от №1 до №15 и еще шар «крест». Бить можно любым шаром по любому. Найдите вероятность того, что при случайном выборе: А) ударят шаром №7 по какому-то другому шару; Б) ударят по шару №7 шаром с наименьшим номером; В) ударят «крестом» по шару №7; Г) ударят «крестом» по шару с двузначным номером А) Решение. Пусть событие А – удар шаром №7 по какому-то другому шару 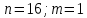  Б) Решение. Пусть событие А – удар по шару №7 шаром с наименьшим номером  Пусть событие Б – выбор шара №7  Пусть событие В – выбор шара с номером меньше 7   В) Решение. Пусть событие А – удар «крестом» по шару №7 Пусть событие Б – выбор шара «крест»  Пусть событие В – выбор шара №7   Г) Решение. Пусть событие А – удар «крестом» по шару с двузначным номером  Пусть событие Б – выбор шара «крест»  Пусть событие В – выбор шара с двузначным номером   Ответ: а) 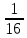 ; б) ; б) 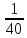 ; в) ; в) 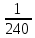 ; г) ; г) 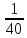 №12. Из 4 шаров, занумерованных числами 1, 2, 3 и 4, наугад выбирают 2 шара. Какова вероятность того, что вынутые шары имеют номера 2 и 3? Решение. Пусть событие А – когда вынутые шары имеют номера 2 и 3    Ответ:  №13. В ящике 1 белый и 3 черных шара. Наугад вынимают 2 шара. Какова вероятность того, что вынуты: 1) 2 черных шара; 2) белый и черный шар? 1) Решение. Пусть событие А – вытягивание 2-х черных шаров    2) Решение. Пусть событие А – вытягивание белого и черного шаров  1 вариант. Если первым достается белый шар.  Пусть событие 1 – вытягивание белого шара    Пусть событие 2 – черного шара     2 вариант. Если первым достается черный шар.  Пусть событие 3 – вытягивание черного шара    Пусть событие 4 – вытягивание белого шара      Ответ: 1)  ; 2) ; 2)  №14. В ящике находятся 2 белых и 2 черных шара. Наугад вынимают 2 шара. Найти вероятность того, что вынуты: 1) 2 белых шара; 2) один белый и один черный шар? 1) Решение. Пусть событие А – вытягивание 2-х черных шаров   2) Решение. Пусть событие А – вытягивание белого и черного шаров  1 вариант. Если первым достается белый шар.  Пусть событие 1 – вытягивание белого шара  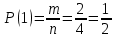 Пусть событие 2 – черного шара 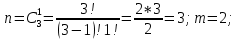 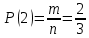 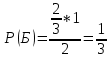 2 вариант. Если первым достается черный шар.  Пусть событие 3 – вытягивание черного шара   Пусть событие 4 – вытягивание белого шара     Ответ: 1)  ; 2) ; 2)  №15. В ящике находится 4 белых и 1 черный шар. Наугад вынимают 2 шара. Найти вероятность того, что вынуты: 1) 2 белых шара; 2) белый и черный шары. 1) Решение. Пусть событие А – вытягивание 2-х белых шаров    2) Решение. Пусть событие А – вытягивание белого и черного шаров  1 вариант. Если первым достается белый шар.  Пусть событие 1 – вытягивание белого шара    Пусть событие 2 – черного шара     2 вариант. Если первым достается черный шар.  Пусть событие 3 – вытягивание черного шара    Пусть событие 4 – вытягивание белого шара      Ответ: 1)  ; 2) ; 2)  №16. Из колоды карт (36 листов) наугад вынимают 2 карты. Какова вероятность того, что это: 1) дама треф и валет пик; 2) две шестерки? 1) Решение. Пусть событие А – вытягивание дама треф и валет пик  1 вариант. Дама треф вытягивается первой.  Пусть событие 1 – вытягивание дамы треф  Пусть событие 2 – вытягивание вальта пик из оставшихся карт   Вариант 2. Валет пик вытягивается первым.  Пусть событие 3 – вытягивание вальта пик  Пусть событие 4 – вытягивание дамы треф из оставшихся карт    2) Решение. Пусть событие А – вытягивание двух шестерок  Пусть событие 1 – вытягивание одной шестерки  Пусть событие 2 – вытягивание вальта пик из оставшихся карт   Ответ: 1)  ; 2) ; 2)  №17. В коробке «Ассорти» - 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова вероятность того, что: а) обе конфеты окажутся с любимой Таниной начинкой – шоколадной; б) обе конфеты – с фруктовой начинкой; в) конфеты с разными начинками; |
