Комбинаторные методы решения вероятностных задач. ДЗ 1. Решение. Пусть событие а получение слова крот
 Скачать 42.8 Kb. Скачать 42.8 Kb.
|
|
г) чему равна сумма вероятностей в пунктах а), б), в)? А) Пусть событие А – вытягивание 2 шоколадных конфеты. 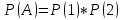 Пусть событие 1 – вытягивание 1 шоколадной конфеты 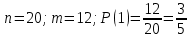 Пусть событие 2 – вытягивание 2-ой шоколадной конфеты из оставшихся 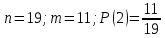 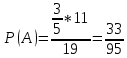 Б) Пусть событие А – вытягивание 2 конфет с фруктовой начинкой 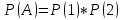 Пусть событие 1 – вытягивание 1 конфеты с фруктовой начинкой 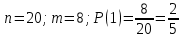 Пусть событие 2 – вытягивание 2-ой конфеты с фруктовой начинкой из оставшихся 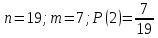 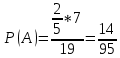 В) Пусть событие А – вытягивание 2-х конфет с разной начинкой 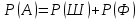 Вариант 1. Пусть событие Ш – вытягивание первой конфеты с шоколадной начинкой 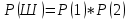 Пусть событие 1 – вытягивание 1-ой конфеты с шоколадной начинкой 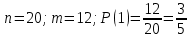 Пусть событие 2 – вытягивание 2-ой конфеты с фруктовой начинкой из оставшихся 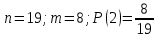 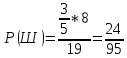 Вариант 2. Пусть событие Ф – вытягивание первой конфеты с фруктовой начинкой 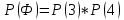 Пусть событие 3 – вытягивание 1-ой конфеты с фруктовой начинкой 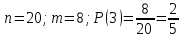 Пусть событие 4 – вытягивание 2-ой конфеты с шоколадной начинкой из оставшихся 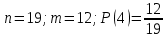 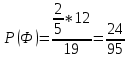 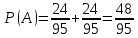 Г) Сумма вероятностей 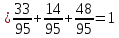 Ответ: а) 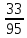 ; б) ; б) 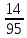 ; в) ; в) 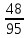 ; г) 1 ; г) 1№18. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что: а) обе они согласные; б) среди них есть «ъ»; в) среди них нет «ъ» г) одна буква гласная, а другая согласная. Решение. А) Пусть событие А – выбор 2-согласных. 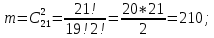 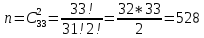 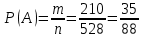 Б) Пусть событие А – одна из букв «Ъ» 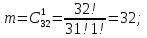 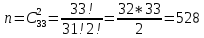 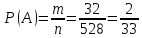 В) Пусть событие А – нет буквы «Ъ» 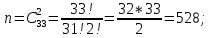 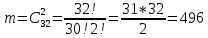 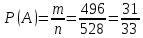 Г) Пусть событие А – одна из букв «Ъ» 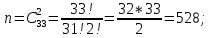 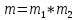 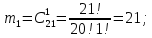 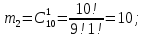 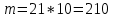 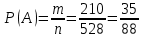 Ответ: а) 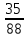 ; б) ; б) 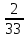 ; в) ; в) 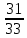 ; г) ; г) 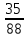 №19. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все 3 тетради окажутся в клетку? Решение. Пусть событие А – выбор трех тетрадей в клетку 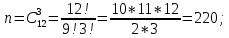 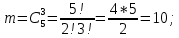 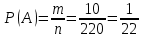 Ответ: 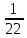 №20. В ящике находятся 10 деталей, одна из которых нестандартная. Наугад берут 2 детали. Какова вероятность того, что обе детали окажутся стандартными? Решение. Пусть событие А – выбор двух стандартных деталей 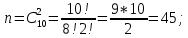 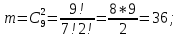 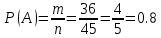 Ответ: 0,8 №21. Четыре билета на ёлку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам? Решение. Пусть событие А – выбор 5-ти карандашей нужного цвета. 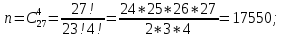 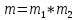 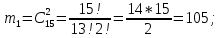 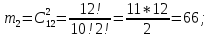 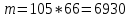 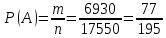 Ответ: 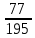 №22. В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 5 карандашей. Какова вероятность того, что 3 из них окажутся красными, а 2 – синими? Решение. Пусть событие А – выбор 5-ти карандашей нужного цвета. 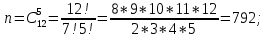 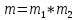 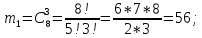 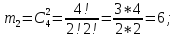 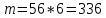 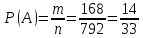 Ответ: 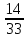 Домашняя работа №23. На полке стоит 12 книг, из которых 4 – это учебники. С полки наугад снимают 6 книг. Какова вероятность того, что 3 их них окажутся учебниками? 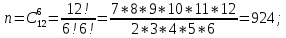 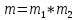 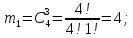 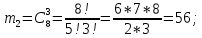 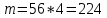 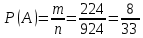 Ответ: 8/33 №24. В ящике находятся 3 белых и 2 черных шара. Наугад вынимаются 2 шара. Какова вероятность того, что вынуты: 1) 2 белых шара; 2) 2 черных шара; 3) черный и белый шары; 4) не 2 белых шара; 5) не разноцветные шары? 1) Пусть событие А – вытягивание 2-х белых шаров 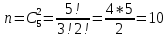 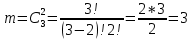 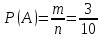 2) Пусть событие А – вытягивание 2-х черных шаров 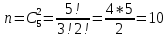 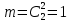 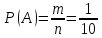 3) Пусть событие А – вытягивание белого и черного шаров 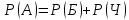 1 вариант. Если первым достается белый шар. 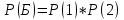 Пусть событие 1 – вытягивание белого шара 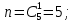 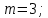 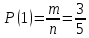 Пусть событие 2 – черного шара 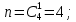 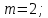 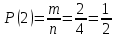 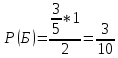 2 вариант. Если первым достается черный шар. 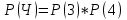 Пусть событие 3 – вытягивание черного шара 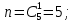 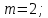 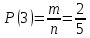 Пусть событие 4 – белого шара 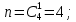 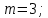 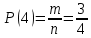 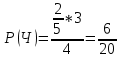 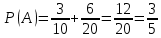 4) не 2 белых шара; Пусть Событие А – выпадают не два белых шара, тогда противоположное ему событие 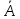 – выпадают 2 белых шара. Данное событие мы уже находили в пункте 1, оно равно – выпадают 2 белых шара. Данное событие мы уже находили в пункте 1, оно равно 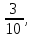 тогда событие А: тогда событие А: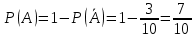 5) не разноцветные шары. Следовательно, должны выпасть либо 2 черных, либо 2 белых шара. Данные вероятности уже посчитаны в пунктах 1 и 2. Сложим их: 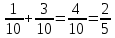 Ответ: 1) 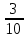 ; 2) ; 2) 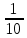 ; 3) ; 3) 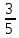 ; 4) ; 4) 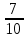 ; 5) ; 5)  №25. Из колоды карт (36 листов) наугад вынуты две карты. Какова вероятность того, что среди них: 1) хотя бы одна карты трефовой масти; 2) хотя бы одна карта – туз? 1) Решение. Пусть событие А – вытягивание карты трефовой масти 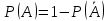 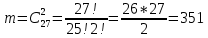 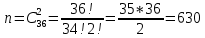 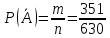 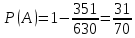 2) Решение. Пусть событие А – вытягивание туза 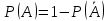 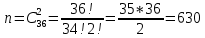 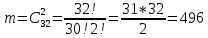 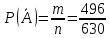 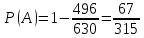 Ответ: 1) 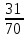 ; 2) ; 2) 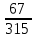 №26. В ящике лежат 6 красных шаров и 4 зеленых. Наугад вынимают 3 шара. Какова вероятность того, что 2 шара из них окажутся красными, а один зеленым? Решение. Пусть событие А – вытягивание шаров нужных цветов 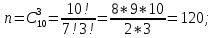 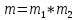 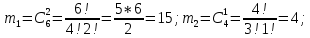 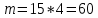 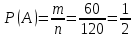 Ответ: 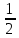 №27. В вазе 11 гвоздик, из которых 4 красные. В темноте наугад вынимают три гвоздики. Какова вероятность того, что, хотя бы одна из них будет красной? Решение. Пусть событие А – вытягивание красной гвоздики 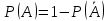 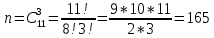 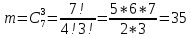 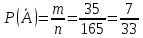 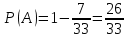 Ответ: 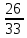 №28. Вы находитесь в круглом зале с 10 дверьми, из которых какие-то 4 заперты. Вы выбираете две двери. Найдите вероятность того, что, хотя бы через одну из них можно выйти из зала? Решение. Пусть событие 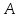 – вероятность выхода из зала, тогда событие – вероятность выхода из зала, тогда событие 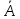 – вероятность, что из зала не выйти – вероятность, что из зала не выйти 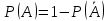 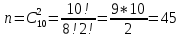 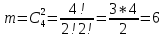 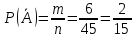 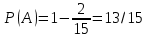 Ответ: 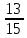 №29. Вы находитесь в круглом зале с 10 дверьми, 5 из которых заперты. Вы выбираете две двери. Найдите вероятность того, что через одну из них можно выйти из зала, но через другую вернуться уже нельзя. 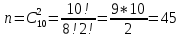 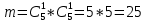 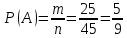 Ответ: 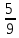 №30. Выяснить, является ли справедливым следующий выбор преимущества среди трех игроков с помощью двух карт красной масти и двух карт черной масти: «Преимущество достается первому игроку, если случайным образом вынуть две карты разных мастей; преимущество достается второму игроку, если вынимают две карты красной масти; преимущество достается третьему игроку, если вынуты обе карты черной масти». Решение: 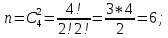 Вероятность для 1-го игрока: 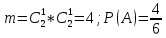 Вероятность для 2-го игрока: 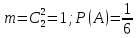 Вероятность для 3-го игрока: 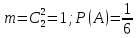 Ответ: выбор не справедливый, так как первый игрок имеет явное преимущество, четыре шанса из шести. №31. Из четырех тузов случайным образом одновременно вытащили две карты. Найдите вероятность того, что: а) обе карты – тузы черной масти; б) среди выбранных карт есть пиковый туз; в) среди выбранных карт есть туз красной масти; г) среди выбранных карт нет бубнового туза. А) Пусть событие А – вытаскивают 2 карты черной масти 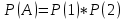 Пусть событие 1 – вытягивание первой карты черной масти |
