Количественные методы в источниковедении - Шендерюк М.Г.. Количественные методы в источниковедении
 Скачать 1.67 Mb.
|
|
Раздел 2. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ МЕТОДЫ 2.1. Первоначальные понятия статистики Преимущественное положение в системе количественных методов, используемых историками, занимают методы математико-статистического анализа. Термин «статистика» происходит от латинского слова «статус» (status) – положение, состояние явлений. Этот термин неоднозначен. Под статистикой понимают совокупность итоговых показателей, количественно характеризующих различные стороны общественной жизни, – экономику, политику, культуру. Под статистикой понимают также практическую деятельность по сбору и обобщению соответствующих данных. Статистикой называют и особую общественную науку. Наука статистика, как и всякая иная наука, возникла из практических потребностей людей. Она имеет богатую историю. Примером совершенствования статистических приемов может служить изменение единицы наблюдения, связанной с налогообложением крестьян в России: в XV-XVI вв. – «соха» (крестьянская община, объединявшая до нескольких десятков дворов), в XVII в. – «двор», в XVIII в. – «ревизская душа» (крепостной крестьянин мужского пола). Предметом статистики выступает количественная сторона массовых общественных явлений, взятая в неразрывной связи с их качественной стороной и отображаемая посредством статистических показателей. Статистический показатель - это число, характеризующее ту или иную особенность, сторону общественных явлений. Все общественные науки объектом своего изучения имеют общество. Объект изучения статистики выступает в виде особых множеств массовых общественных явлений – статистических совокупностей. Статистической совокупностью называется множество объективно существующих во времени и пространстве явлений, однокачественных в определенной связи. Отдельные первичные неделимые элементы, или индивидуальные явления, составляющие статистическую совокупность, называются единицами совокупности, а число элементов совокупности – объемом совокупности. С категорией статистической совокупности тесно связан широко известный закон больших чисел. Законом больших чисел называется весьма широкий принцип взаимопогашения (уравновешивания) случайных факторов (колебаний), наблюдающихся у индивидуальных явлений, в результате которого могут отчетливее проявиться внутренние необходимые связи явлений. Закон больших чисел является одним из выражений диалектической связи между случайностью и необходимостью, он помогает выявлять необходимое там, где на поверхности выступает игра случайностей. С помощью закона больших чисел в статистических совокупностях устанавливаются имеющиеся в явлениях необходимые закономерные уровни и соотношения – статистические закономерности. Статистическая закономерность по своей природе близка к закону. Она так же, как и закон, отражает необходимые причинно-следственные связи. Однако эти связи здесь менее устойчивы, не всеобщи, как в законе, а относятся к определенному пространству и времени, справедливы лишь для данных условий развития конкретных явлений. Связь и различие между статистикой и математикой заключается в том, что обе эти науки исследуют количественную сторону явлений, но математика исследует количественную сторону всех явлений (природы и общества) безотносительно к качеству, а статистика – количественную сторону лишь общественных явлений и всегда определенного качества. В статистике применяется математика различных уровней. Длительное время статистики обходились в своей работе простейшими приемами элементарной математики (правилами арифметики, алгебраическими выражениями и т.п.). Но необходимость познания массовых случайных процессов вызвала к жизни и призвала на помощь статистикам специальный раздел высшей математики – математическую статистику. Исследованием случайных процессов занимается теория вероятностей. Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Метод исследования, опирающийся на рассмотрении статистических данных о тех или иных совокупностях объектов, называется статистическим. Статистический метод применяется в самых различных областях знания. Однако черты статистического метода в применении к объектам различной природы столь своеобразны, что было бы бессмысленно объединять, например, социально-экономическую статистику, физическую статистику, звездную статистику и т.п. в одну науку. Общие черты статистического метода в различных областях знания сводятся к подсчету числа объектов, входящих в те или иные группы, рассмотрению распределения количественных признаков, применению выборочного метода, использованию теории вероятностей при оценке достаточности числа наблюдений для тех или иных выводов и т.п. Эта формальная математическая сторона статистических методов исследования, безразличная к специфической природе изучаемых объектов, и составляет предмет математической статистики. Связь математической статистики с теорией вероятностей имеет в разных случаях различный характер. Теория вероятностей изучает не любые массовые явления, а явления случайные и именно «вероятностно случайные», т.е. такие, для которых имеет смысл говорить о соответствующих им распределениях вероятностей. Случайное событие – это событие, которое может наступить, в тех же условиях – не наступить или происходить иначе. Теория вероятностей – математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми. Тем не менее теория вероятностей играет определенную роль и при статистическом изучении массовых явлений любой природы, которые могут не относиться к категории вероятностно случайных. Это осуществляется через основанные на теории вероятностей теорию выборочного метода и теорию ошибок. В этих случаях вероятностным закономерностям подчинены не сами изучаемые явления, а приемы их исследования. Методы математической статистики позволяют решать несколько типов исследовательских задач:
2) задачи статистического оценивания параметров генеральной совокупности по выборочным данным; 3) задачи статистического анализа взаимосвязей; 4) задачи классификации объектов или признаков; 5) задачи сжатия информации. Рассмотрим, как решаются эти задачи в исторических исследованиях с помощью основных математико-статистических методов. 2.2. Методы дескриптивной (описательной) статистики Для анализа статистической совокупности прежде всего используются обобщающие количественные показатели, которые позволяют описать изучаемое явление или процесс в целом, показывая тенденцию его развития. Основными описательными характеристиками статистической совокупности являются средняя арифметическая, дисперсия и среднее квадратическое отклонение. Прежде чем приступить к изучению статистической совокупности, необходимо на содержательном уровне выявить, является ли она качественно однородной. Широко известно, например, что земские статистики абсолютизировали однородность российского крестьянства, поэтому опубликованные сводные данные земско-статистических обследований превратились в тома средних цифр, нивелирующих существенные различия в экономическом состоянии разных типов крестьянских хозяйств. Для анализа статистической совокупности удобно ее упорядочить в возрастающем или убывающем порядке, такая совокупность называется вариационным (ранжированным) рядом, а единицы совокупности – вариантами (обозначаются xi , где  – номер варианты). Изменение (вариация) признака, по которому обследуются объекты, может быть дискретным или непрерывным. При дискретной вариации значения варианты отличаются на некоторую конечную величину и вариационный ряд называется дискретным. При непрерывной вариации отдельные значения признака могут отличаться на сколь угодно малую величину и вариационный ряд называется интервальным.Существуют две группы характеристик вариационного ряда: средние величины и меры вариации (рассеяния) признака. Средняя представляет собой количественную характеристику качественно однородной совокупности. Наиболее распространенными средними являются средняя арифметическая, мода и медиана. Средняя арифметическая ( 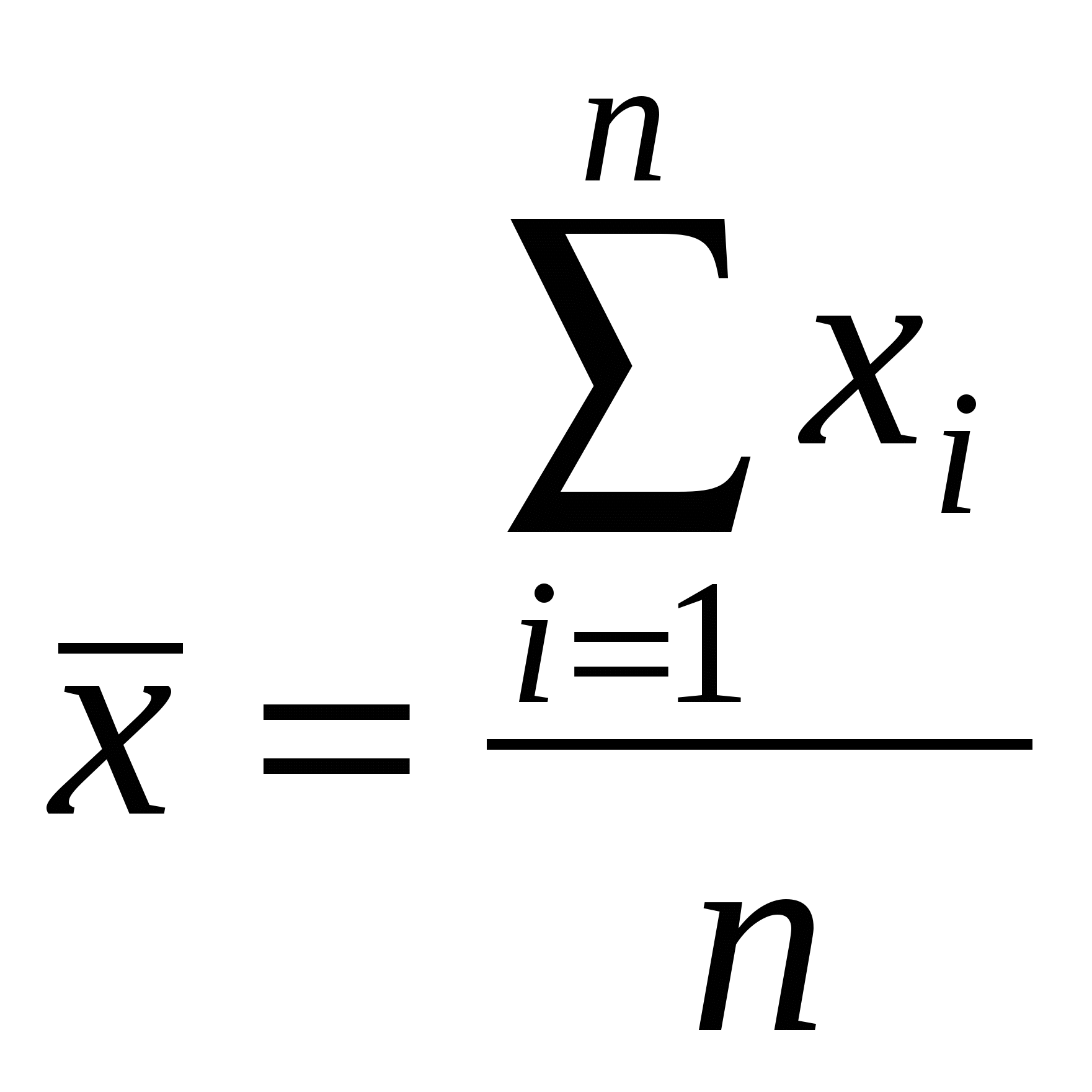 ) – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле: , (2.2.1)где xi - варианта с порядковым номером (=1,…n); n – объем совокупности.Мода (Мо) – варианта, которая чаще всего встречается в данном вариационном ряду. Медиана (Ме) – варианта, находящаяся в середине вариационного ряда: Ме=  , если число вариант нечетно (n=2m+1);Ме=  , если число вариант четно (n=2m).Медиана используется, когда изучаемая совокупность неоднородна. Особое значение она приобретает при анализе ассиметричных рядов (рядов, у которых нагружены крайние значения вариант). Медиана дает более верное представление о среднем значении признака, т.к. она не столь чувствительна к крайним (нетипичным в плане постановки задачи) значениям как средняя арифметическая. Средние позволяют охарактеризовать статистическую совокупность одним числом, однако не содержат информации о том, насколько хорошо они представляют эту совокупность. Для определения того, насколько сильно варьируются значения признака, используются такие характеристики, как размах вариации, дисперсия и среднее квадратическое отклонение. Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:  . (2.2.2)Показатель этот достаточно просто рассчитывается, однако является наиболее грубым из всех мер рассеяния, поскольку при его определении используются лишь крайние значения признака, а все другие просто не учитываются. При расчете двух других характеристик меры вариации признака используются отклонения всех вариант от средней арифметической. Эти характеристики (дисперсия и среднее квадратическое отклонение) нашли самое широкое применение почти во всех разделах математической статистики. Дисперсия (2) – абсолютная мера вариации (колеблемости) признака в статистическом ряду - средний квадрат отклонения всех значений признака ряда от средней арифметической этого ряда: 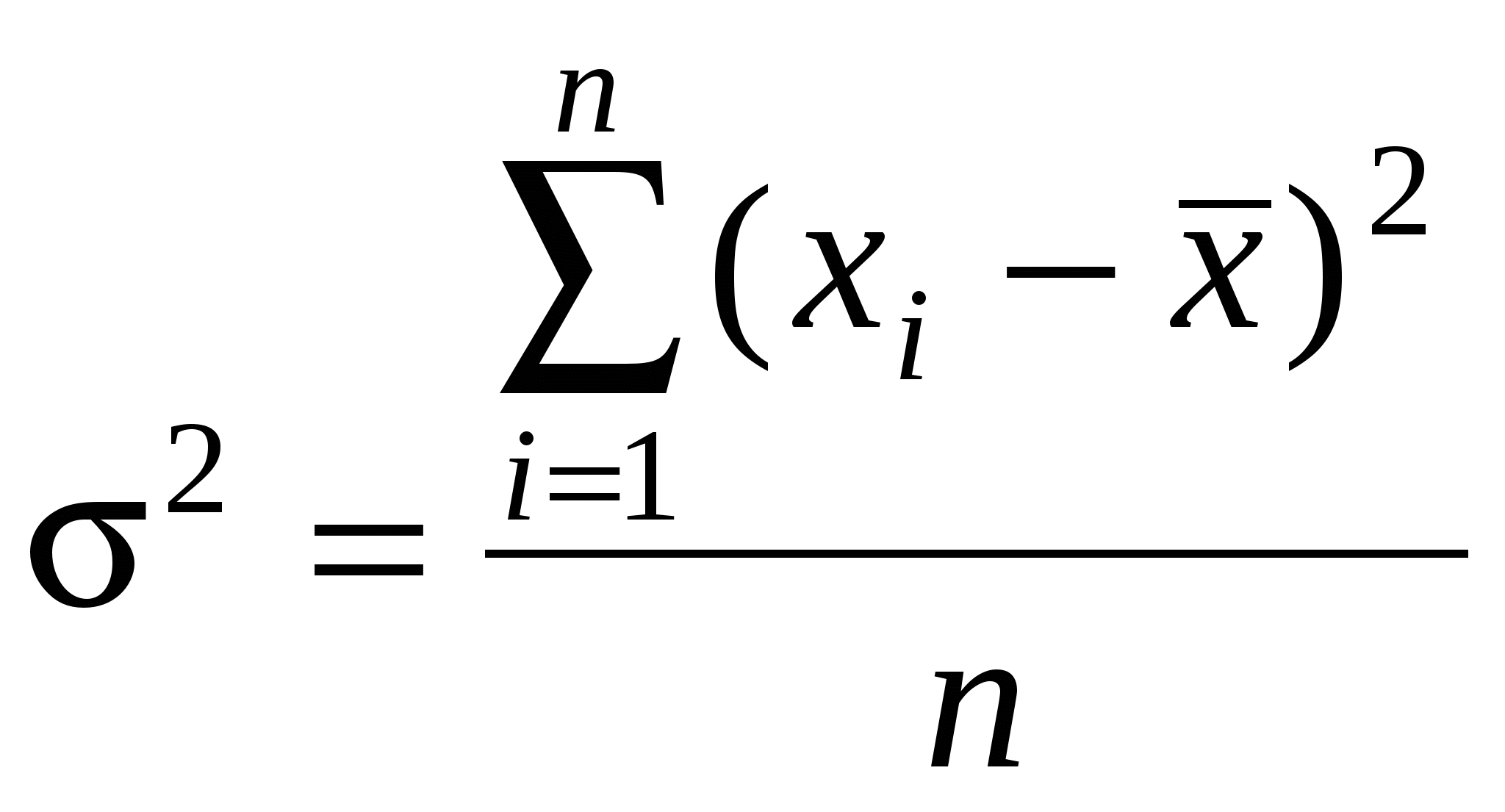 , (2.2.3)где xi - варианта с порядковым номером ;  - средняя арифметическая; n – объем совокупности. Для представления меры вариации в тех же единицах, что и варианты, используется среднее квадратическое отклонение. Среднее квадратическое отклонение () – это квадратный корень из дисперсии: 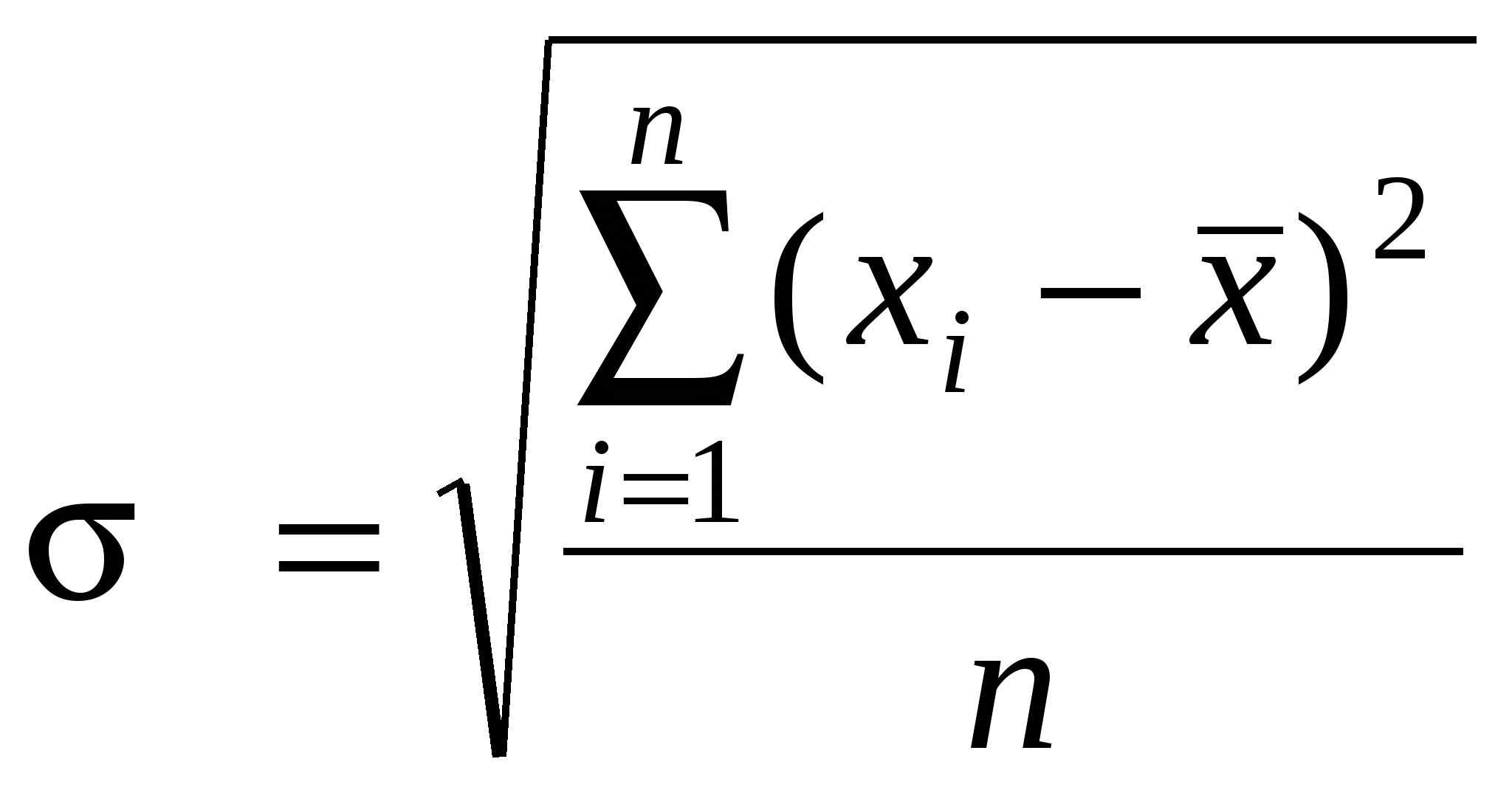 . (2.2.4)Рассмотренные меры рассеяния – абсолютные величины. Однако часто бывает необходимо сравнить вариацию одного и того же признака у разных групп объектов, выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, сопоставить вариацию разных признаков у одних и тех же групп объектов. Для решения этих задач необходимо использовать относительные показатели. Таким показателем является коэффициент вариации. Коэффициент вариации (V) – это отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:  . (2.2.5)Пример 1. Даны две группы людей, возраст которых (в годах): 1 группа: 27; 29; 30; 31; 31; 32; 2 группа: 13; 14; 14; 15; 61; 63. Вычислим средний возраст для каждой группы. Получим, что и в первой, и во второй группе средний возраст одинаков и равен 30 годам. Тогда как очевидно, что для первой группы эта величина представительна, в ней действительно собраны 30-летние, а вторую группу она абсолютно не характеризует, т.к. в ней – подростки и пенсионеры. Тогда обратимся к характеристикам меры вариации признака. Вычислим среднее квадратическое отклонение и коэффициент вариации для обеих групп по формулам (2.2.4) и (2.2.5). Получим  ,  ,  ,  .Таким образом, сравнение коэффициентов вариации позволяет говорить о значительных различиях рассматриваемых групп: первая группа представляет собой достаточно однородную совокупность, а вторая группа таковой не является. Важную роль в изучении вариационных рядов играет их графическое изображение (термин «дескриптивный» переводится не только как «описательный», но и как «изобразительный», «наглядный»). Существует несколько способов графического изображения рядов (диаграмма, гистограмма, полигон, кумулята и др.), выбор которых зависит от вида вариационного ряда и цели исследования. Однако общим для всех типов графиков является то, что они показывают частоту встречаемости различных значений данного признака - распределение значений признака. Пример 2. В архивных фондах ГАКО выявлено 288 анкет-заявлений глав переселенческих семей, прибывших в колхозы и совхозы Калининградской области в 1947 году согласно правительственной программе заселения и освоения сельских районов нового края6. Анализ содержания анкет-заявлений позволил выделить основные признаки, которые служат хорошей иллюстрацией социального облика переселенца. Рассмотрим, например, признак «стаж работы в колхозе». Средний стаж работы в колхозе составлял 10 лет (при среднем возрасте 36 лет). Однако это число нивелирует имевшие место существенные различия в стаже. Рассмотрим диаграмму и гистограмму распределения переселенцев по стажу работы в колхозе. 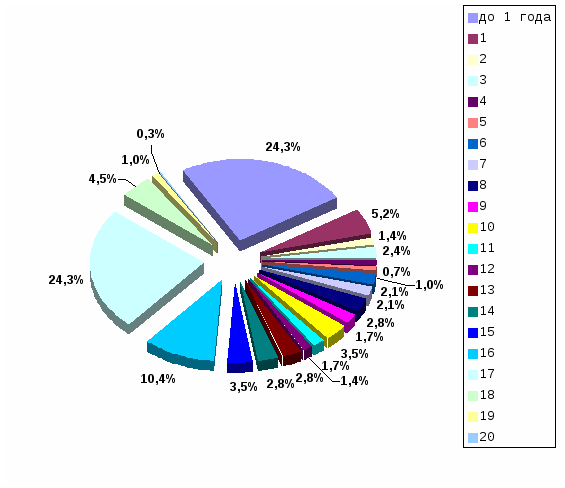 Рис. 1. Диаграмма распределения переселенцев по стажу работы в колхозе 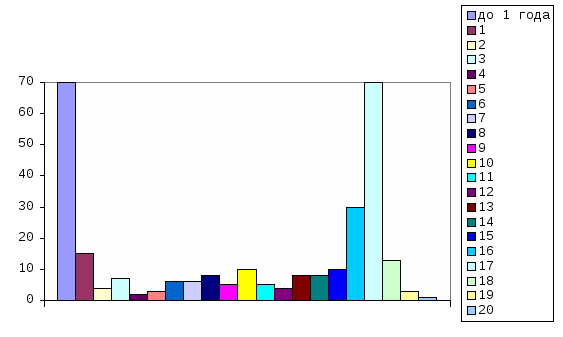 Рис. 2. Гистограмма распределения переселенцев по стажу работы в колхозе Как показывают графики, выделилось две крупные группы (по 70 человек каждая, т.е. по 24,3%), охватив около половины всех переселенцев, со стажем менее года и со стажем 17 лет. Это свидетельствует о том, что население сельских районов новой области в первую очередь формировалось как теми, кто работал в колхозах страны с начала коллективизации (с 1930 г.), так и людьми, еще вчера не имевшими отношения к сельскому хозяйству (значительную часть последней категории составляли демобилизованные из Советской Армии). Часто графическое изображение распределения значений признака используется для его сопоставления с нормальным, т.е. для проверки гипотезы о том, что значения данного признака распределены по нормальному закону. Нормальное распределение играет особую роль в теоретико-прикладном плане, поскольку нормальность является существенным условием корректности применения статистических методов. Графически нормальное распределение изображается в виде симметричной одновершинной кривой, напоминающей по форме колокол. Высота (ордината) каждой точки этой кривой показывает, как часто встречается соответствующее значение. Форма нормальной кривой и положение ее на оси абсцисс полностью определяются двумя параметрами: средним арифметическим значением  и средним квадратическим отклонением  . Вершина кривой соответствует среднему арифметическому значению, т.е. наиболее часто встречаются значения, близкие к среднему, а по мере удаления от него частота падает.Каждому значению признака х соответствует определенное значение так называемой функции распределения  , показывающее, какова вероятность существования значений, меньших данного значения х. Геометрически вероятность значений, меньших данного х, изображается площадью под кривой распределения слева от этого значения. Площадь под всей кривой равна 1, что соответствует полной достоверности, т.е. вероятности того, что признак вообще принимает какое-то (любое) значение.В силу своей важности для практических приложений функция нормального распределения табулирована, т.е. существуют специальные таблицы, в которых каждому значению x ставится в соответствие вероятность F(x) существования значений, меньших x. Для удобства табулирования в качестве значений признака берутся не сами величины x, а так называемые нормированные отклонения их от среднего значения t, где  .При замене x на t центр распределения смещается в точку 0, а единицей измерения становится величина среднего квадратического отклонения , но вид кривой распределения не изменяется. Среднее значение нормированного отклонения t равно 0, а его среднее квадратическое отклонение равно 1. Нормированная функция нормального распределения обладает следующими свойствами:     . |