Количественные методы в источниковедении - Шендерюк М.Г.. Количественные методы в источниковедении
 Скачать 1.67 Mb.
|
|
2.3. Выборочный метод Множество всех единиц статистической совокупности называется генеральной совокупностью. На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Одна из двух проблем очень часто стоит перед историком: как по немногим сохранившимся данным получить широкую и достоверную историческую картину и как из многочисленных сведений отобрать минимальное количество данных, по которым можно было бы судить обо всем явлении в целом. Обе проблемы удовлетворительно решаются с помощью хорошо разработанного в математической статистике выборочного метода. Из генеральной совокупности особым образом отбирается часть элементов - формируется выборка, и результаты обработки выборочных данных распространяются на всю генеральную совокупность. Теоретической основой выборочного метода является закон больших чисел. Однако для характеристики всей генеральной совокупности могут служить лишь репрезентативные (представительные) выборки, т.е. выборки, которые правильно отражают свойства генеральной совокупности. В статистике доказано: чтобы выборка была репрезентативной, она должна быть случайной, т.е. каждая единица генеральной совокупности должна иметь равный шанс попасть в выборку. Таким образом, задачей исследователя, в распоряжении которого имеются сплошные данные, является организация выборочного изучения этих данных путем формирования репрезентативной выборки. Если же он имеет дело с данными ранее проведенных выборочных обследований, необходимо проверить, как были организованы эти обследования, не нарушались ли принципы случайного отбора. Сложнее решить вопрос о репрезентативности так называемых «естественных выборок», поскольку надежных математических методов проверки их репрезентативности не существует. Здесь на первый план выступает изучение истории происхождения данных и их содержательный анализ. Существует несколько видов выборочного изучения, позволяющих формировать репрезентативные выборки: случайный, механический, типический и серийный отбор. Случайным является такой отбор, при котором все элементы генеральной совокупности имеют равную возможность быть отобранными. На практике случайный отбор производится с помощью жеребьевки или использования разработанных в статистике таблиц случайных чисел. При жеребьевке может осуществляться бесповторный отбор (когда выбранный элемент больше не участвует в выборке) или повторный (когда ему предоставляется шанс еще раз быть выбранным). При большом объеме генеральной совокупности проведение жеребьевки или использование таблиц случайных чисел становятся затруднительными, тогда применяют другие виды выборочного изучения. Механический отбор сводится к тому, что генеральная совокупность разбивается на равные части и из каждой части берется одна единица. Например, 7, 17, 27, 37 и т.д. Однако механическим отбором следует пользоваться очень осторожно, поскольку элементы исходной совокупности могут быть упорядочены, что может привести к возникновению систематических ошибок. Необходимо проанализировать изучаемую совокупность и применять механический отбор лишь в том случае, если элементы генеральной совокупности расположены случайным образом. Механический отбор достаточно широко использовался в русской статистике. Например, механический отбор применялся земскими статистиками для обследований части крестьянских хозяйств не по обычной подворной карточке, а по особой расширенной программе. С помощью механического отбора изучалось состояние 25 млн. крестьянских хозяйств и накануне сплошной коллективизации, когда они были подвергнуты 10%-ному весеннему опросу и 5%-ному осеннему опросу. Типический отбор заключается в том, что генеральная совокупность разбивается на типические группы, образованные по какому-либо признаку. Затем из каждой выделенной группы отбираются единицы либо случайно, либо механически. Например, территория, подлежащая обследованию, разделяется на районы, отличающиеся социально-экономическими или географическими условиями, и из каждого района производят отбор единиц в выборку. При этом допускается как отбор, пропорциональный численности отдельных типических групп, так и непропорциональный. Понятно, что более предпочтительным является пропорциональный отбор, поскольку он дает более точные результаты. Серийный отбор предусматривает разбиение всей генеральной совокупности на группы (серии), из которых путем случайного или механического отбора выделяется их определенная часть, которая и подвергается сплошной обработке. Фактически, серийный отбор представляет собой случайный или механический отбор, произведенный для укрупненных элементов исходной совокупности. Например, обследуются не единичные крестьянские хозяйства, а целые деревни или имения. Итак, выборочный метод позволяет экстраполировать результаты обследования выборки на всю генеральную совокупность. При этом надо иметь в виду, что всегда будет возникать некоторая ошибка, показывающая, насколько хорошо характеристики выборки отражают соответствующие характеристики генеральной совокупности. Ошибки, возникающие при использовании выборочных данных для суждения обо всей генеральной совокупности, называются ошибками репрезентативности. Они бывают систематическими и случайными. Систематические ошибки – ошибки, возникающие при использовании выборочных данных, если не выполняются условия случайного отбора. Случайные ошибки – ошибки, возникающие при использовании выборочных данных за счет того, что для анализа всей совокупности используется только ее часть. Величина ошибки выборки – это разность между генеральной и выборочной средними. В математической статистике существуют формулы для вычисления средней ошибки выборки на основе данных той выборки, с которой работает исследователь. Для различных видов выборочного изучения средняя ошибка выборки определяется по-разному. Рассмотрим формулы вычисления средней ошибки выборки при случайном отборе. Средняя ошибка выборки () при случайном повторном отборе определяется формулой:  = , (2.3.1)где - оценка среднего квадратического отклонения в генеральной совокупности по выборке; n – объем выборки. Средняя ошибка выборки при случайном бесповторном отборе:    , (2.3.2)где N – объем генеральной совокупности. Средняя ошибка малой выборки, т.е. выборки, объем которой не превышает 30 единиц, вычисляется по формуле: = . (2.3.3)Средняя ошибка выборки позволяет по выборочной средней судить о значении генеральной средней. Однако в конкретном выборочном исследовании ошибка может существенно отличаться от средней ошибки, превышая ее. Поэтому более эффективным является определение тех границ, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы определяются предельной ошибкой выборки () по формуле: =t, (2.3.4) где t – коэффициент, вычисляемый по специальной таблице; - средняя ошибка выборки. Коэффициент t определяется задаваемой исследователем вероятностью P (0P1). Для значений P, приближающихся к единице, практически исключается возможность того, что генеральная средняя будет отличаться от вычисленной выборочной средней больше, чем на . Со своей стороны указывает точность, гарантируемую заданным уровнем надежности (вероятности P). При этом, чем выше уровень вероятности (используются, например, значения 0,90; 0,95; 0,99 и др.), тем выше коэффициент t, а следовательно, и значение предельной ошибки . Поэтому на практике приходится довольствоваться некоторым компромиссом между противоречивыми требованиями максимальной надежности и максимальной точности. Таким образом, разность между генеральной и выборочной средними не будет превышать по модулю значения предельной ошибки выборки:  , (2.3.5)тогда можно определить интервал, в котором практически наверняка находится генеральная средняя, – доверительный интервал:  , (2.3.6)при этом всегда указывается надежность этого результата (значение P, которое использовалось при вычислении ). Для малой выборки предельная ошибка выборки вычисляется по формуле:  , (2.3.7)где t рассчитывается исходя из так называемого закона распределения Стьюдента с степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения),  .Связь между коэффициентом t и вероятностью P в распределении Стьюдента сложнее, чем в нормальном распределении и определяется с учетом объема выборки. Пример 3. По урожайности зерновых культур 10 колхозов определить среднюю и предельную ошибки выборки и оценить пределы для генеральной средней. Исходные данные (xi, i = 1,…10 - урожайность зерновых в центнерах с гектара) и промежуточные вычисления можно записать в таблице:
Получим: 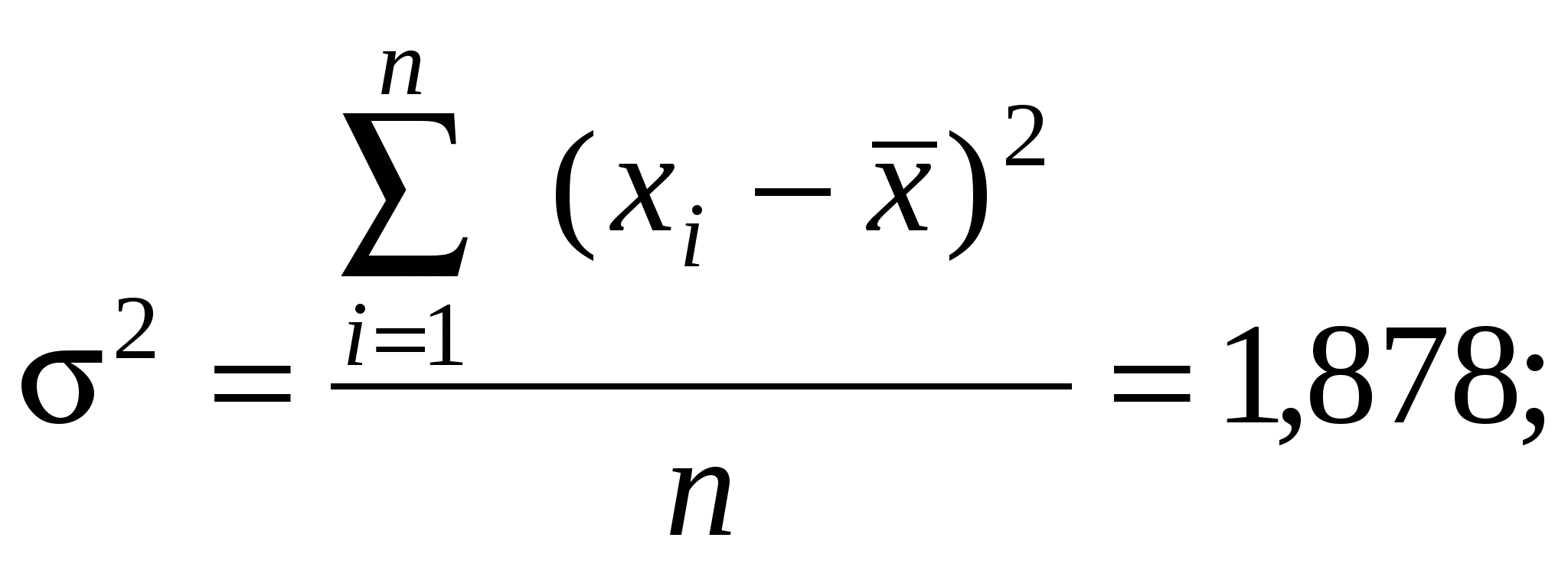    Для P=0,95 t=2,26 =t  1,04  Очевидно, что полученная предельная ошибка (15%) слишком велика и объем выборки в 10 единиц не достаточен для суждения о реальной средней урожайности зерновых. Важным вопросом в выборочном методе является определение необходимого объема выборки. Как правило, объем выборки определяется на основе содержательного анализа данных, например, в 10% или 20%. Обычно выборки такого объема бывает достаточно для получения надежных результатов. Однако можно определить объем выборки по специальной формуле. Для этого необходимо: 1) провести пробную 1 %-ную выборку и вычислить для нее выборочную среднюю и дисперсию; 2) задать необходимую предельную ошибку выборки и уровень надежности P; 3) найти объем выборки по формуле:  , (2.3.8)где  - дисперсия признака, вычисленная по пробной выборке;  - заданная точность результатов выборочного исследования (заданная предельная ошибка выборки); t - табличный коэффициент, соответствующий заданной надежности результатов выборочного изучения (вероятности P). Если пробная выборка мала (n<30), то при определении коэффициента t учитывается также объем пробной выборки.Пример 4. Для рассмотренных в примере 3 данных об урожайности зерновых культур в колхозах определим требуемый объем выборки. Зададим предельную ошибку выборки, равную 5%, она будет равна =0,34, тогда, подставляя в формулу (6.8) значения t=2,26; =1,37 и , получим n=86. Таким образом, для определения средней урожайности зерновых в колхозах с вероятностью 95% и точностью 5% необходимо произвести выборку, объемом 86 единиц. 2.4. Корреляционный анализ В реальной исторической действительности существует диалектическое взаимодействие и взаимообусловленность во всех явлениях и процессах. При этом часто воздействие одних признаков на другие осуществляется столь скрыто и опосредованно, что уловить его без специального методического инструментария практически невозможно. Решить эту задачу позволяют хорошо разработанные в статистике методы корреляционного и регрессионного анализа. Зависимости, которые присущи объективным явлениям природы и общества, делятся на функциональные и статистические. Функциональная зависимость – это взаимосвязь между признаками, при которой каждому значению одного признака соответствует единственное значение другого признака. Простейшей формой функциональной связи является линейная зависимость, которая характеризуется уравнением:  . (2.4.1)Другими формами функциональной зависимости, применяемыми в статистическом анализе, являются парабола (  ), гипербола ( ), логарифмическая функция ( ), экспонента ( ).Функциональная зависимость предполагает изолированность взаимосвязанных признаков от воздействия других факторов. Но такая ситуация в явлениях общественной жизни практически не встречается. Здесь на связь между признаками влияет множество других факторов, и она проявляется лишь в тенденции, «в среднем». Такая зависимость называется статистической, или корреляционной. Статистическая (корреляционная) зависимость – это взаимосвязь между признаками, при которой одному и тому же значению одного признака могут соответствовать различные значения другого признака. Для выявления степени статистической зависимости между признаками используются методы корреляционного анализа. Корреляционный анализ – совокупность методов математической статистики, позволяющих обнаружить корреляционную зависимость между случайными величинами или признаками и оценить значимость этой связи. Теснота связи определяется коэффициентом корреляции. Основной мерой связи в корреляционном анализе является линейный коэффициент корреляции, который измеряет степень линейной зависимости между признаками. Парный линейный коэффициент корреляции определяет тесноту связи между двумя признаками и рассчитывается по формуле: 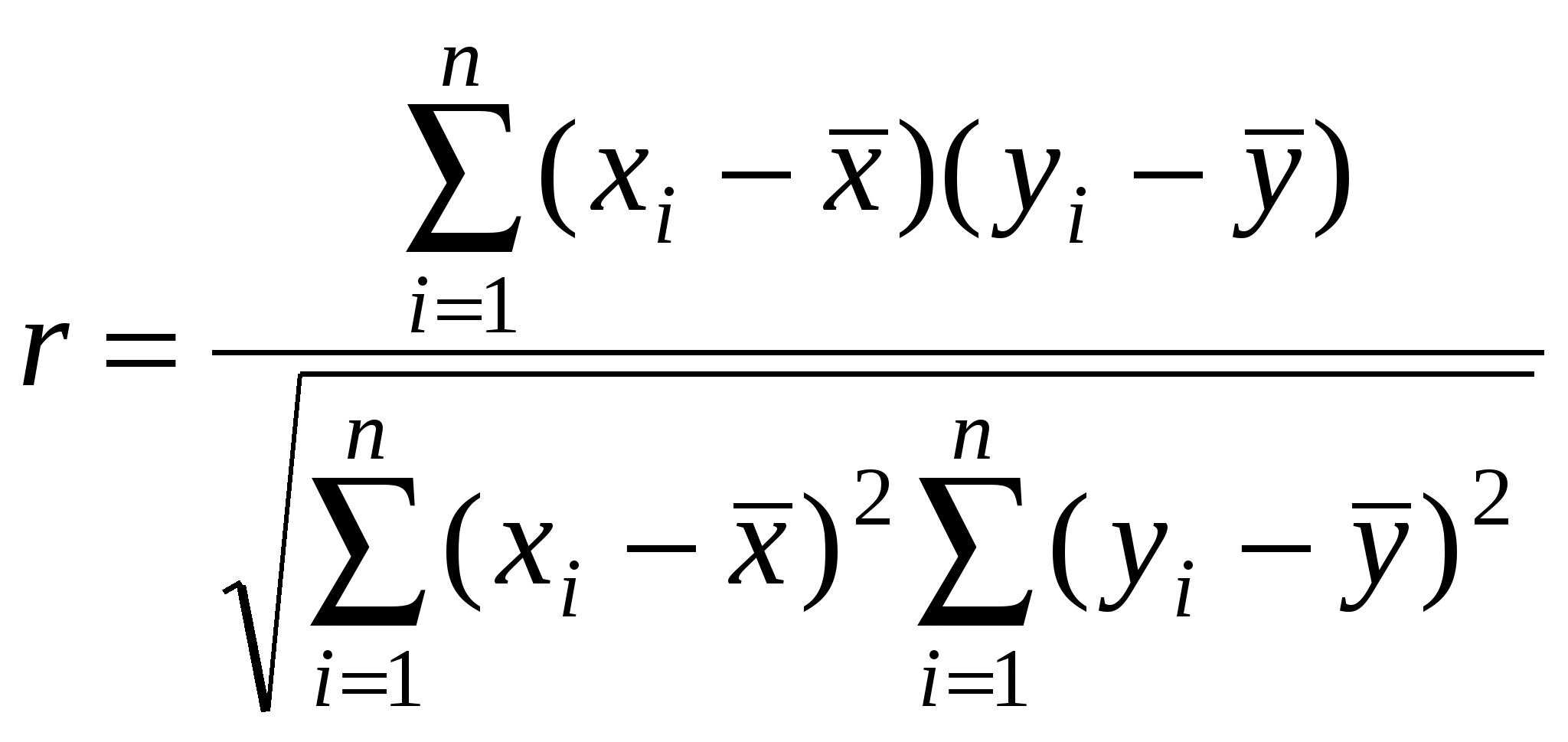 , (2.4.2)где  - значения признаков x и y для i-го объекта; n - число объектов;  - средние арифметические значения признаков x и y.Линейный коэффициент корреляции может принимать значения от -1 до +1. Чем ближе величина коэффициента корреляции к предельным значениям, тем теснее взаимосвязь между признаками. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи между признаками. Если коэффициент корреляции равен +1 (или -1), то между признаками существует прямая (или обратная) функциональная зависимость. При содержательном анализе взаимосвязей часто необходимо не только оценить тесноту связи между изучаемыми признаками, но и определить степень воздействия одного признака на другой. Для решения этой задачи используется коэффициент детерминации. Коэффициент детерминации – показатель, определяющий долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака:  , (2.4.3)где r - коэффициент корреляции. Пример 5. Определим степень корреляционной зависимости между доходом и размерами помещичьего хозяйства в России на рубеже XIX-XX вв. по сведениям о размерах (в десятинах) и доходах (в тыс. руб.) десяти помещичьих имений7. Априори ясно, что доходность имения росла вместе с увеличением его размеров. Однако доходность имения, помимо его размеров, определялась еще качеством земли, состоянием хозяйства, деловыми способностями его владельца, близостью рынка, уровнем агротехники и другими факторами. Поэтому интересно узнать, насколько все-таки доходность определялась именно размерами имения. Исходные данные (xi - размеры имения в десятинах, yi - доход имения в тыс. руб.) и промежуточные вычисления запишем в таблице:
Получим:  ;    .Таким образом, доход имения примерно на 76% объясняется и обусловливается его размерами и на 24% - другими факторами. Коэффициент корреляции рассчитывается, как правило, для выборочных данных, поэтому существуют приемы проверки значимости вычисленного коэффициента корреляции для всей генеральной совокупности. Рассмотрим, как определяется значимость парного линейного коэффициента корреляции для случая малой выборки (практически для n<50 ): 1) вычисляется статистическая характеристика  , подчиняющаяся закону распределения Стьюдента, по формуле: , (2.4.4)где r - вычисленный выборочный коэффициент корреляции; n - объем выборки. 2)  сравнивается с табличной, или критической, величиной  , зависящей от числа  и от заданной вероятности  :а) если  , то можно сделать вывод о наличии связи;б) если  , то гипотеза об отсутствии связи не отклоняется.Пример 6. Проверим значимость коэффициента корреляции, вычисленного в пятом примере. Вычислим  по формуле (2.4.4):  . Зададим вероятность  , найдем для этой вероятности табличное значение  , получаем  .Таким образом, с вероятностью 99% связь между доходностью и размерами помещичьих имений существует. Зависимость между тремя и большим числом признаков изучается методами многомерного корреляционного анализа с помощью вычисления частных и множественных коэффициентов корреляции8. 2.5. Регрессионный анализ Анализ статистической зависимости предполагает не только оценку тесноты связи между признаками, но и выявление ее формы. Эта задача решается методами регрессионного анализа. Регрессионный анализ – это совокупность методов математической статистики, позволяющих определить форму связи между результативным и факторным признаками, установленной корреляционным анализом. Корреляционная связь описывается с помощью уравнения регрессии. Уравнение регрессии – это описание корреляционной связи с помощью подходящей функции. Простейшее уравнение линейной регрессии имеет вид:  , (2.5.1)где x - факторный признак; y - результативный признак; a и b - параметры уравнения, которые могут быть найдены методом наименьших квадратов по формулам: 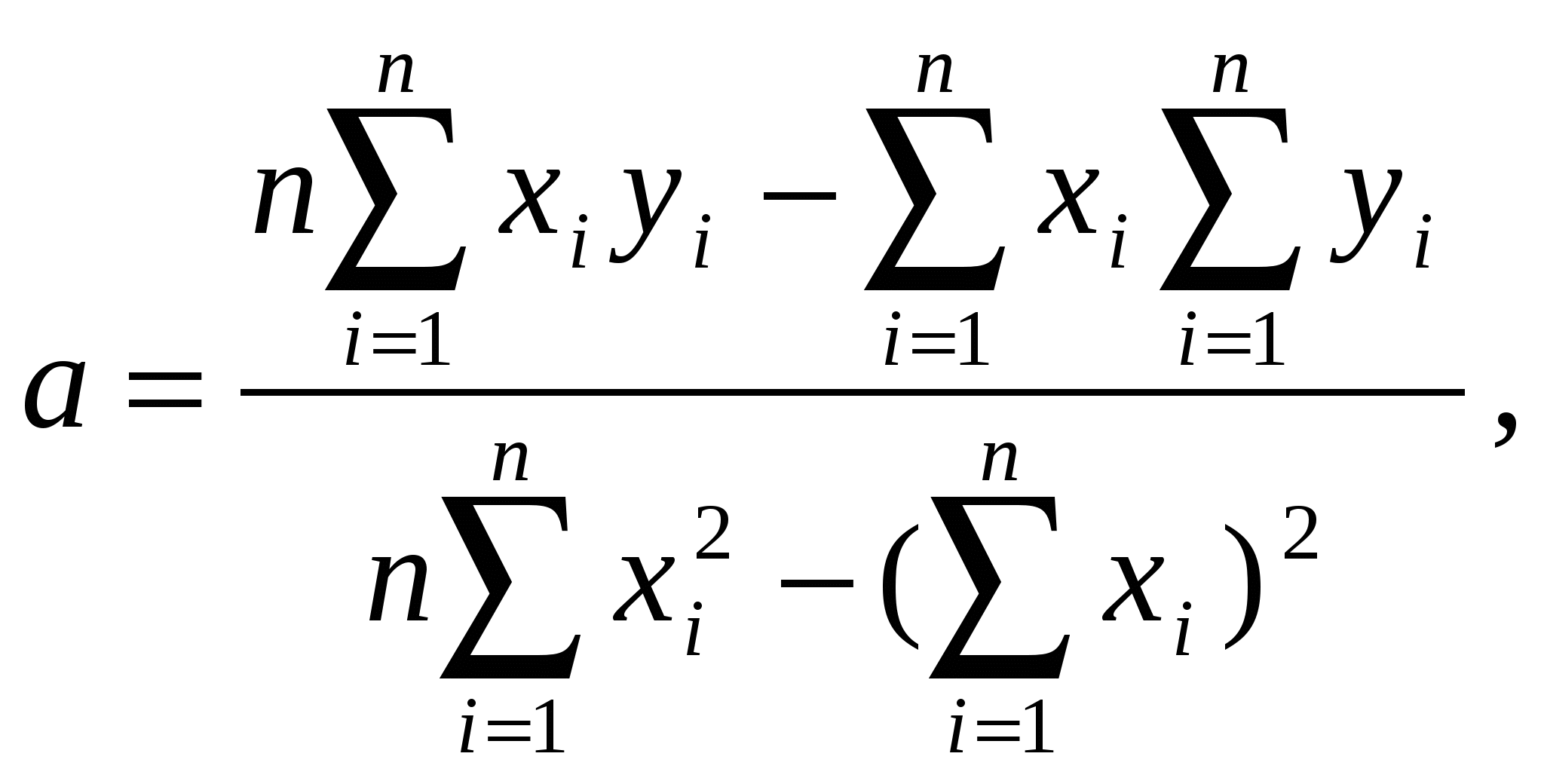  , (2.5.2)где  -  -е значение признаков x и y соответственно;  - средние арифметические признаков x и y; n - число значений признаков x и y.Коэффициент a называется коэффициентом регрессии. Он показывает, на какую величину в среднем изменяется результативный признак y при изменении факторного признака x на единицу. Если коэффициент регрессии положительный, то между результативным и факторным признаками наблюдается прямая зависимость: с ростом значения факторного признака значение результативного признака растет, и, наоборот, с уменьшением значения факторного признака значение результативного признака уменьшается. Если же коэффициент регрессии отрицательный, между признаками наблюдается обратная связь: с ростом значения факторного признака значение результативного признака уменьшается, и, наоборот, с уменьшением значения факторного признака значение результативного признака растет. Метод наименьших квадратов позволяет выбрать «наилучшую» среди всех возможных прямых в том смысле, что она проходит «ближе всего» к точкам диаграммы рассеяния - изображения объектов как точек на плоскости двух признаков. Пример 7. Найдем уравнение линейной регрессии, описывающее корреляционную связь между размерами и доходом помещичьего имения по данным примера 5. Запишем промежуточные вычисления в таблице:
Вычислим параметры a и b по формулам (2.5.2):  , b=1,61–0,00606·290= –0,1474.Уравнение линейной регрессии примет вид: y=0,00606x–0,1474. Коэффициент регрессии в этом уравнении, равный 0,00606, означает, что при возрастании размеров имения на единицу, т.е. на 1 десятину, доход имения возрастает на 0,00606 тыс. рублей, или на 6,06 рублей. С помощью уравнения регрессии можно предсказать примерный доход имения любых размеров. Изобразим графически диаграмму рассеяния по данным десяти имений и прямую регрессии, описываемую полученным уравнением линейной регрессии (рис. 3). 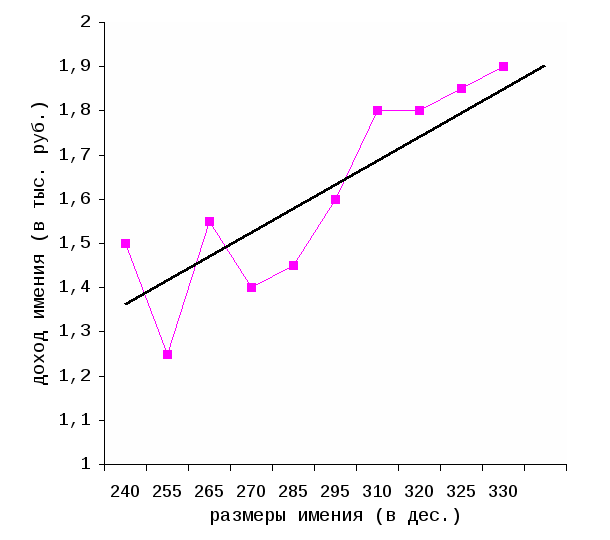 Рис. 3. График зависимости дохода помещечьего имения от его размеров Прямая регрессии показывает тенденцию в изменении дохода имения в зависимости от его размеров. Мы рассмотрели лишь наиболее простую форму связи между двумя признаками - линейную. Однако, во-первых, зависимости между признаками могут принимать самые разнообразные формы, а, во-вторых, при более полном анализе взаимосвязей необходимо учитывать, что на результативный признак обычно влияет не один фактор, а несколько. Выявить форму связи между результативным признаком и несколькими факторными признаками позволяет множественный регрессионный анализ9. 2.6. Кластерный анализ Важнейшей задачей исторической науки является классификация изучаемых объектов и явлений. Традиционно такая классификация сводится к группировке объектов на основе одного (двух-трех) признаков. Однако современные методы многомерного статистического анализа и компьютерные технологии позволяют учитывать при группировке все существенные структурно-типологические признаки (их может быть несколько десятков). Методы, на основе которых все схожие объекты можно собрать в одну группу, и при этом объекты из разных групп будут существенно отличаться, составляют совокупность методов автоматической классификации (кластерного анализа, таксономии). Кластерный анализ – совокупность методов, составляющих раздел многомерного статистического анализа, с помощью которых осуществляется построение многомерной классификации объектов. Основная идея кластерного анализа заключается в последовательном объединении группируемых объектов по принципу наибольшей близости – схожести свойств. Процедура построения классификации состоит из последовательности шагов, на каждом из которых производится объединение двух ближайших групп объектов (кластеров10). Рассмотрим агломеративно-иерархический метод кластерного анализа. Пусть существует n объектов, каждый из которых характеризуется набором из m признаков. Каждый из этих объектов может быть представлен точкой в m-мерном пространстве признаков. О сходстве объектов можно судить по расстоянию между соответствующими точками: чем ближе точки расположены друг к другу, тем более схожи их свойства. Евклидово расстояние между точками определяется формулой:  (i, j = 1,2,…,n), (2.6.1)где  - евклидово расстояние между i-м и j-м объектами;  - значение k-го признака для i-го объекта. Подсчитав значения расстояний для всех пар объектов, получим квадратную симметричную матрицу D размером n×n ( 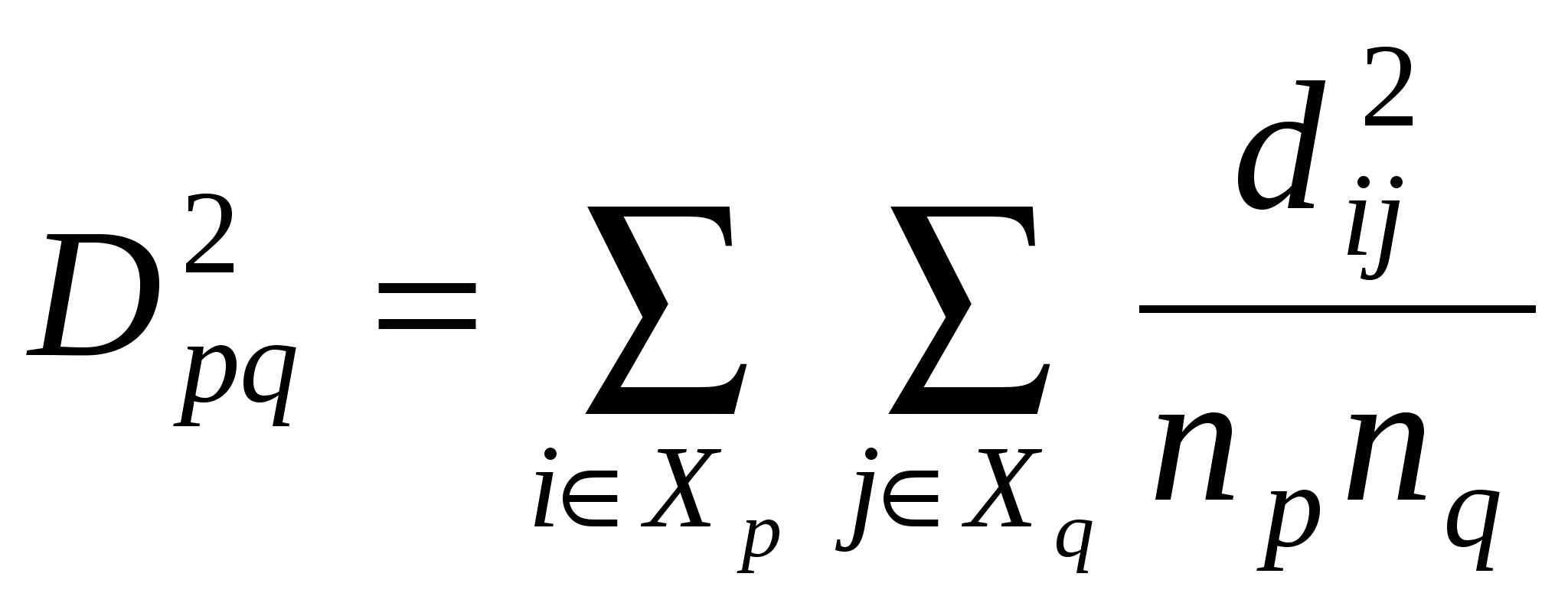 ,  =0). На основе матрицы D можно вычислить расстояния между кластерами. Близость двух кластеров определяется как среднее значение расстояния между всеми такими парами объектов, где один объект пары принадлежит к одному кластеру, а другой - к другому: , (2.6.2)где  - мера близости между p-м и q-м кластерами;  - p–й кластер;  - q-й кластер;  - число объектов в p-м и q-м кластерах соответственно.На первом шаге процедуры построения классификации в матрице расстояний D выбирается минимальное расстояние между объектами и объекты, находящиеся друг от друга на этом расстоянии, объединяются в один кластер. В матрице вычеркиваются строка и столбец, соответствующие первому из этих объектов, а расстояния от полученного кластера до всех остальных объектов вычисляются по формуле (2.6.2) и заносятся в строку и столбец матрицы расстояний, соответствующие второму объекту из первого кластера. На втором шаге в матрице, содержащей уже n-1 строк и столбцов, снова выбирается минимальное расстояние и формируется новый кластер. Этот кластер может быть построен в результате объединения либо двух объектов, либо одного объекта с первым кластером. В матрице вычеркиваются строка и столбец и пересчитываются расстояния до второго кластера, и т.д. Таким образом, процедура агломеративно-иерархического метода кластерного анализа состоит из n-1 аналогичных шагов, на каждом из которых происходит объединение двух ближайших кластеров (на первых шагах – объектов). В конце этой процедуры, на (n-1)-м шаге, получается кластер, объединяющий все n объектов. Результаты построения многомерной классификации обычно изображают в виде дерева иерархической структуры (дендрограммы), содержащего n уровней, каждый из которых соответствует одному из шагов последовательного укрупнения кластеров. Существенным вопросом в кластерном анализе является установление необходимого и достаточного числа кластеров. Как правило, это число определяется из показателей однородности и близости кластеров – внутригрупповой вариации. Пример 8. Рассмотрим результаты кластерного анализа 10 уездов Новгородской губернии на основе земско-статистических данных, характеризующих крестьянское хозяйство Новгородской губернии на уездном уровне. Исходя из содержательного анализа набора показателей поуездных сводок земских переписей, было выделено 19 относительных признаков группировки. Результаты построения с помощью кластерного анализа классификации 10 объектов (уездов Новгородской губернии) в 19-мерном пространстве признаков отражены на рис. 4. Представленная дендрограмма наглядно раскрывает структуру классификации уездов Новгородской губернии в системе показателей крестьянского хозяйства. Исследуемые объекты разделились на три кластера, в каждый из которых вошли наиболее сходные в аграрном отношении уезды. Близость их выражается межкластерным расстоянием. Образованные кластерами районы губернии можно условно именовать «северный» (I), «центральный» (II) и «южный» (III). В северный район входят три северных территориально смежных уезда – Белозерский, Тихвинский и Устюженский; в южный – два южных (Демянский и Валдайский); центральный район образуют три западных (Новгородский, Крестецкий и Старорусский) и два северо-восточных (Кирилловский и Череповецкий) уезда11.  Рис. 4. Структура многомерной классификации уездов Новгородской губернии (дендрограмма) 2.7. Факторный анализ Методы корреляционного анализа позволяют выявить структуру взаимосвязей признаков, характеризующих изучаемое явление или процесс, но они не дают ответа на вопрос: чем обусловлена именно такая структура связей? Известно, что связь между признаками может объясняться не только их взаимозависимостью, но и воздействием на рассматриваемые признаки неких общих, скрытых, глубинных причин – общих факторов, измерить которые непосредственно невозможно. Определить причины, обусловившие данную структуру взаимосвязей признаков, можно с помощью методов факторного анализа. Факторный анализ – раздел многомерного статистического анализа, объединяющий методы анализа структуры множества признаков, характеризующих изучаемые явления и процессы, и выявления обобщенных факторов. Основное предположение факторного анализа заключается в том, что корреляционные связи между большим числом наблюдаемых показателей определяются существованием меньшего числа гипотетически наблюдаемых показателей или факторов. Объясняя множество исходных признаков через небольшое число общих факторов, факторный анализ осуществляет сжатие информации, содержащейся в исходных коррелированных признаках. Основными характеристиками факторного анализа являются факторные нагрузки и факторные веса. Факторные нагрузки - это значения коэффициентов корреляции каждого из исходных признаков с каждым из выявленных факторов. Чем теснее связь данного признака с рассматриваемым фактором, тем выше значения соответствующих факторных нагрузок. Положительный знак факторной нагрузки указывает на прямую (а отрицательный знак – на обратную) связь данного признака с фактором. Значение факторной нагрузки, близкое к нулю, говорит о том, что этот фактор практически не влияет на данный признак. Таблица факторных нагрузок (табл. 1) содержит m строк (по числу признаков) и k столбцов (по числу факторов). Данные о факторных нагрузках позволяют судить о выборе исходных признаков, отражающих тот или иной фактор, и об относительной доле отдельных признаков в структуре каждого фактора. Факторные веса – это количественные значения (мера проявления) выделенных факторов для каждого из n имеющихся объектов. Объектам с большими значениями факторных весов свойственна большая степень проявления свойств, присущих данному фактору, т.е. большая степень их развития в соответствующем фактору аспекте. В большинстве методов факторного анализа (например, в центроидном, в методе главных компонент, в методе экстремальной группировки параметров и др.) факторы определяются как стандартизированные показатели со средним арифметическим значением 0 и средним квадратическим отклонением 1. Поэтому положительные факторные веса соответствуют тем объектам, которые характеризуются степенью проявления свойств больше средней, а отрицательные факторные веса соответствуют тем объектам, в которых степень проявления свойств меньше средней. Таблица 1 Факторные нагрузки
Таблица факторных весов (табл. 2) содержит n строк (по числу объектов) и k столбцов (по числу факторов). Таблица 2 Факторные веса
Данные о факторных весах определяют ранжировку объектов по каждому фактору. Значения факторных весов можно рассматривать как значения индекса, характеризующего уровень развития объектов в рассматриваемом аспекте. Факторные веса могут быть основой для классификации исследуемых объектов. Создание многомерной типологии на основе факторного анализа оказывается особенно эффективным, когда имеется большое число признаков, характеризующих совокупность объектов, а их содержательный отбор представляет значительные трудности – выбрать наиболее информативные критерии группировки бывает далеко не просто. В такой ситуации необходимо начать со «сжатия» информации, а затем проводить классификацию по любому из выделенных факторов. При этом даже если группировка осуществляется на основе лишь одного фактора, она будет многомерной, поскольку даже в этом случае учитываются несколько исходных показателей. Примером эффективного использования факторного анализа в историческом исследовании служит работа И.Д.Ковальченко и Л.И.Бородкина, посвященная изучению аграрной структуры районов Европейской России на рубеже XIX-XX веков12. Факторный анализ аграрного развития губерний Европейской России позволил исследователям не только охарактеризовать основные компоненты аграрной структуры и определить их сравнительные доли, но и получить обобщенные характеристики общего уровня аграрного развития отдельных районов и губерний страны. Надо отметить, что область аграрно-исторических исследований является наиболее широким полем применения факторного анализа. Так, например, интересны результаты многомерной классификации 290 общин Симбирской губернии по данным 34 исходных показателей земских подворных переписей, осуществленной К.Б.Литваком на основе метода экстремальной группировки параметров факторного анализа13. С целью получить модели хозяйства зажиточного, беднейшего и среднего крестьянства автор объединил 34 исходных показателя в один фактор хозяйственной состоятельности крестьянского хозяйства, затем всю совокупность из 290 общин разбил на три группы. По мнению К.Б.Литвака, такая методика значительно эффективнее традиционных методов классификации, поскольку в данном случае отпадает проблема выбора критериев группировки, а образовавшиеся группы селений более однородны. В данном разделе были рассмотрены основные методы математической статистики, нашедшие самое широкое применение в исторических исследованиях. При этом за пределами изложения остались такие важные сюжеты, как статистический анализ динамических рядов, анализ взаимосвязей качественных признаков, дисперсионный анализ и др. Для освоения этих методов рекомендуется обращение к специальной литературе и пакетам статистических программ (например, к пакету STATISTICA). |
)(
)
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 
… 