Варианты заданий РГЗ Линейные пространства. Линейные преобразова. Комплект заданий для выполнения расчетнографической работы

• Название: Комплект заданий для выполнения расчетнографической работы
• Дата: 27.12.2020
• Размер: 1.02 Mb.
• Имя файла: Варианты заданий РГЗ Линейные пространства. Линейные преобразова.doc
• Тип: Документы; #164608
• страница: 6 из 6

2 Определите размерность и укажите какой-нибудь базис пространства решений линейной однородной системы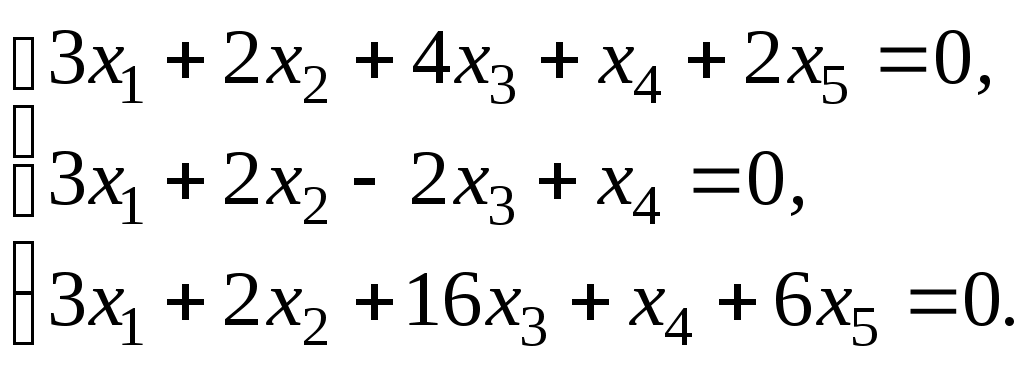

3 Вектор задан своими координатами в базисе . Найдите его координаты в базисе , если , , .
4 Пусть . Выясните, являются ли линейными преобразования, указанные ниже:

а) ;

б) ;

в) .

В случае линейности преобразования, найдите его матрицу в том же базисе.
5 Матрица 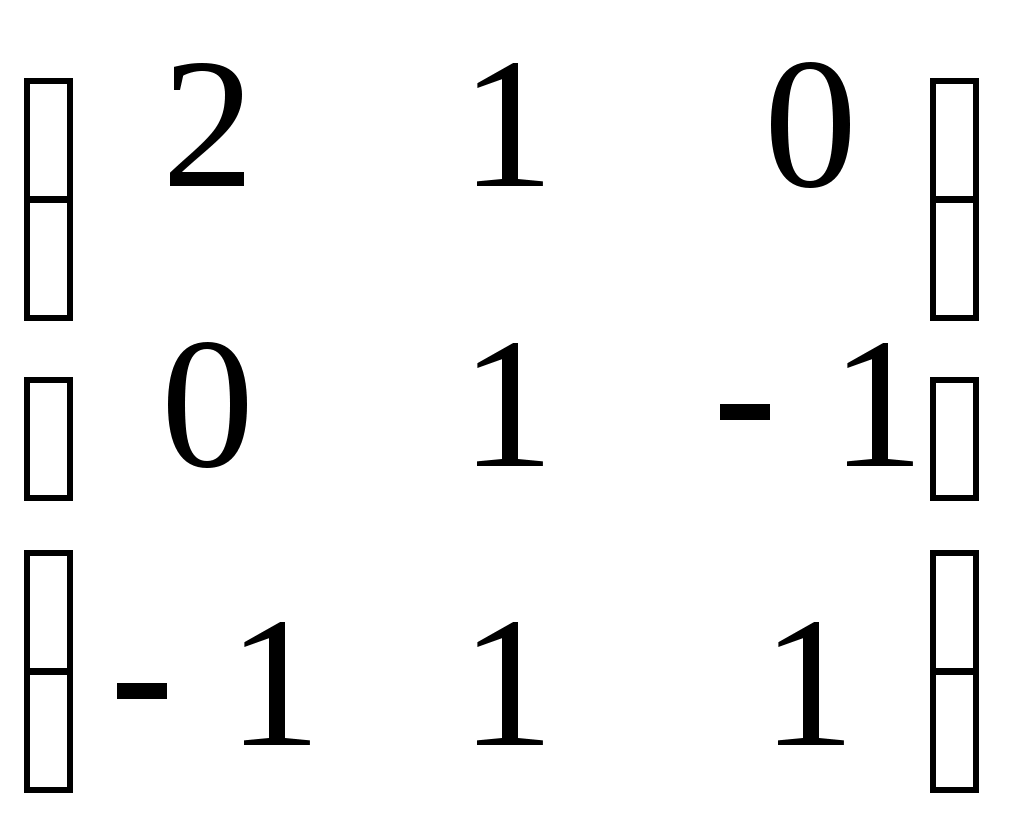линейного преобразования А задана в базисе . Найдите её в базисе , если , , .
6 Матрица линейного преобразования А в некотором базисе имеет вид: 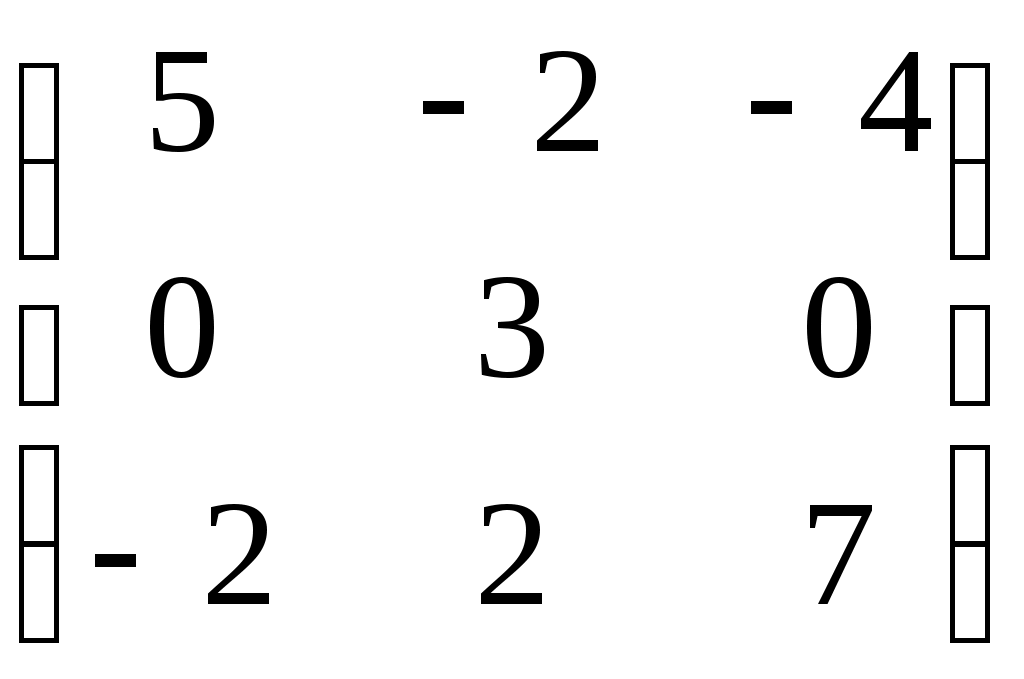. Найдите собственные значения линейного преобразования и собственные векторы, им соответствующие.


Вариант 30

1 Векторы заданы своими координатами в некотором базисе. Докажите, что векторы образуют базис и найдите координаты вектора в этом базисе.
2 Определите размерность и укажите какой-нибудь базис пространства решений линейной однородной системы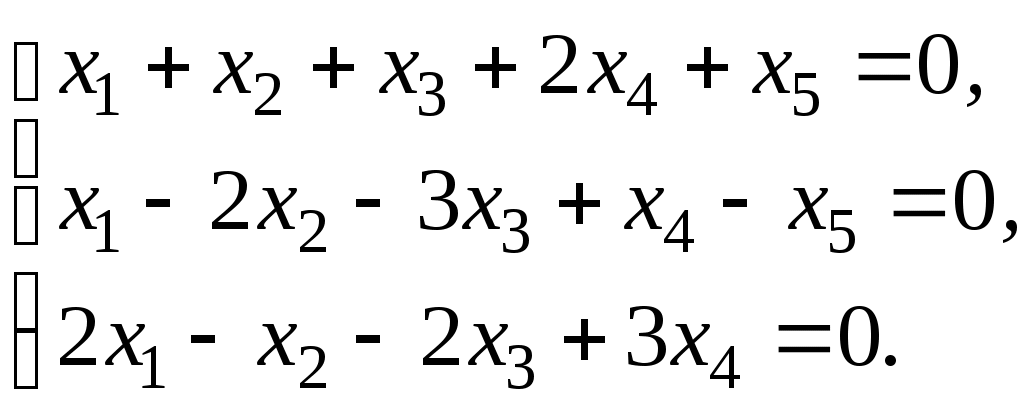

3 Вектор задан своими координатами в базисе . Найдите его координаты в базисе , если , , .
4 Пусть . Выясните, являются ли линейными преобразования, указанные ниже:

а) ;

б) ;

в) .

В случае линейности преобразования, найдите его матрицу в том же базисе.
5 Матрица 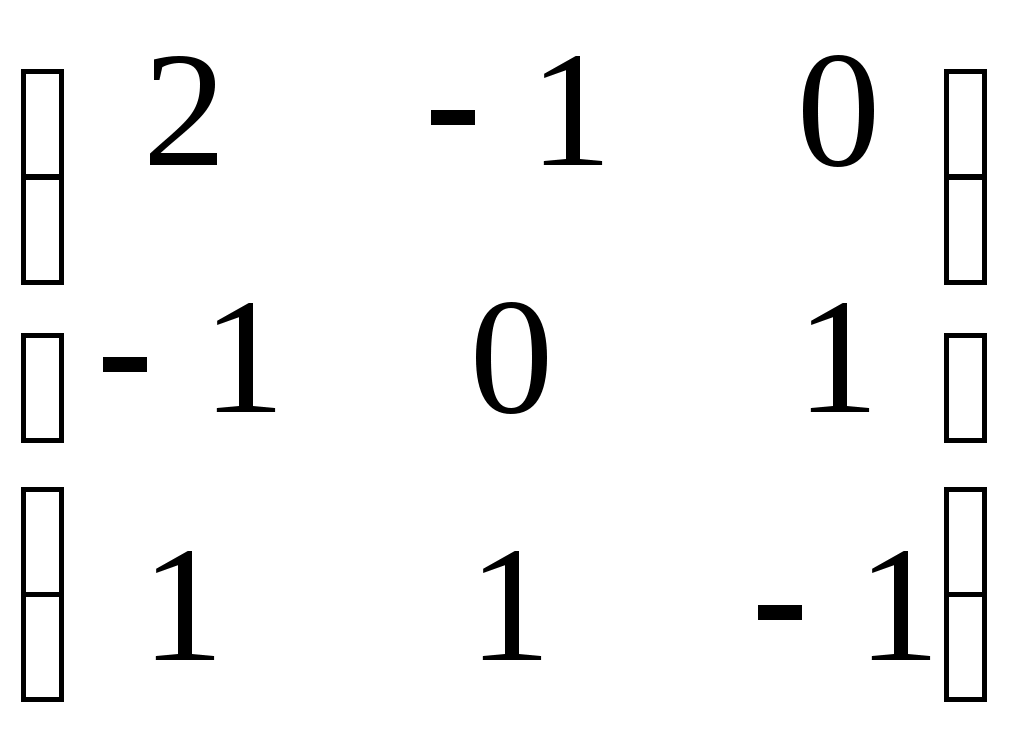линейного преобразования А задана в базисе . Найдите её в базисе , если , , .
6 Матрица линейного преобразования А в некотором базисе имеет вид: 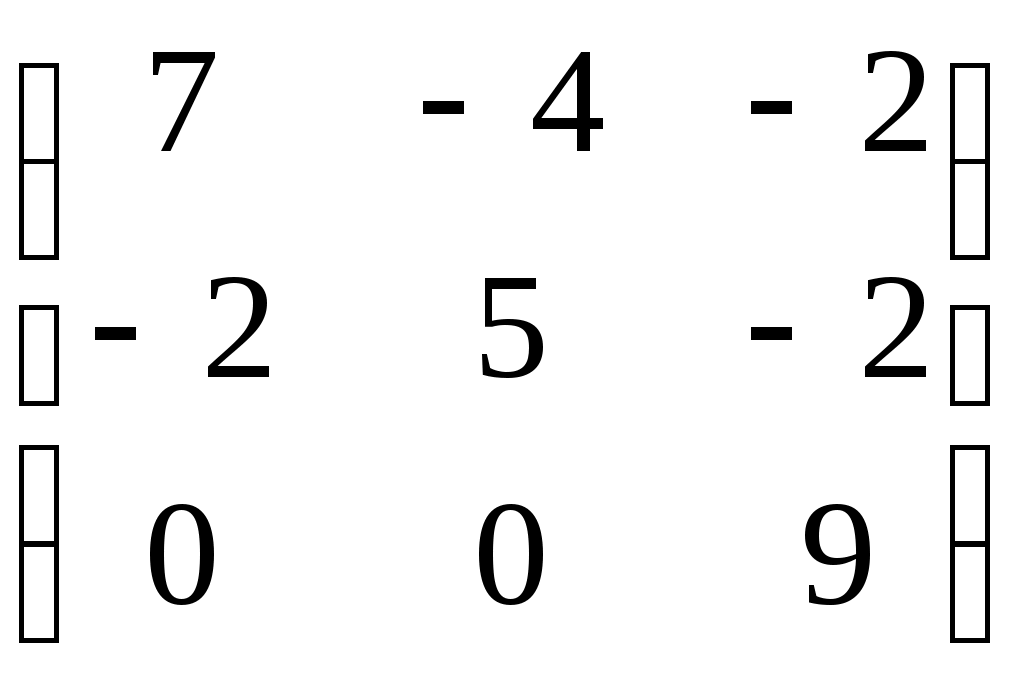. Найдите собственные значения линейного преобразования и собственные векторы, им соответствующие.


Критерии оценки
Правильные решения указанных выше заданий (для каждого варианта) оцениваются по следующему правилу:

• 
  задание 1 - 15 баллов;
  
• 
  задание 2 - 15 баллов;
  
• 
  задание 3 - 15 баллов;
  
• 
  задание 4а) – 5 баллов;
  
• 
  задание 4б) – 5 баллов;
  
• 
  задание 4в) – 5 баллов;
  
• 
  задание 5 - 20 баллов;
  
• 
  задание 6 – 20 баллов;
  

т.е. всего – 100 баллов.

Оценка студенту выставляется в зависимости от числа набранных им баллов:
- оценка «отлично» выставляется студенту, если он набрал 95 – 100 баллов;
- оценка «хорошо» выставляется студенту, если он набрал 75 – 95 баллов;
- оценка «удовлетворительно» выставляется студенту, если он набрал – 60 – 74 балла;
- оценка «неудовлетворительно» выставляется студенту, если он набрал 0 – 59 баллов.



Составитель ________________________ И. Г. Руцкова

^{(подпись)}

«____»__________________20 г.