Конспект лекций по дисциплине Электротехника и электроника
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
Первый закон КирхгофаФормулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла. Формулировка №2:Алгебраическая сумма всех токов в узле равна нулю. Поясню первый закон Кирхгофа на примере рисунка 2. 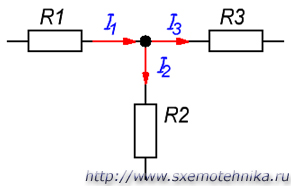 Рисунок 2. Узел электрической цепи. Здесь ток I1- ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать: I1 = I2 + I3 (1) Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим: I1 - I2 - I3 = 0 (2) Знаки «минус» в выражении (2) и означают, что токи вытекают из узла. Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)). Второй закон Кирхгофа.Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре. Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму: 1. Выбираем направление обхода контура (два варианта либо по часовой, либо против). 2. Произвольно выбираем направление токов через элементы цепи. 3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам: - ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-». - напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-». Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке. 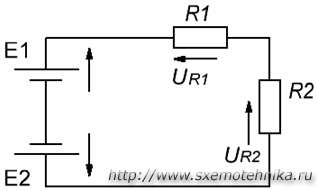 Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа. E1- Е2 = -UR1 - UR2или E1 = Е2 - UR1 - UR2 (3) Энергия и мощность в цепях пост. тока. Закон Дж. Ленца. Уравнение энергетического баланса. В цепях постоянного тока эл. энергия, вырабатываемая источниками, равна энергии, потребляемой приемниками. а) Энергия электрического тока. Для создания электрического тока в цепи источник должен обладать необходимой энергией. Величина этой энергии определяется по формуле: 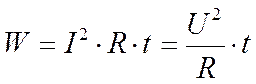 Где: W – энергия электрического тока, Вт·ч U – напряжение на зажимах цепи, В. I – сила тока, А. R – сопротивление цепи, Ом. t – время протекания тока, час. б) мощность электрического тока Различные источники электрической энергии могут за один и тот же промежуток времени выдавать различное количество электрической энергии. Способность источника выдавать в единицу времени определенное количество электрической энергии, а потребитель, соответственно, – потреблять эту энергию характеризуется мощностью источника (потребителя). Значение мощности электрического тока определяется из выражения: 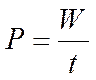 или или 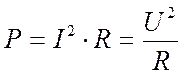 Где: W – энергия электрического тока, Вт·ч t - время работы источника (потребителя), час. Р – мощность источника (потребителя), Вт. U – напряжение, В I – сила тока, А. R – сопротивление цепи, Ом. Энергетический баланс в электрических цепях При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющиеся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за это же время источниками питания. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид: Когда схема питания не только от источников ЭДС , но и от источников тока , тогда при составлении уравнения энергетического баланса необходимо учесть энергию, доставляемую источниками тока. При этом общий вид уравнения энергетического баланса: где падение напряжения между узлами схемы a и b. 3.7. Последовательное и параллельное соединение электрических цепей с сопротивлениями. Проводимость. Последовательное соединение сопротивлений Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R2, конец второго — с началом третьего R3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1). Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же. 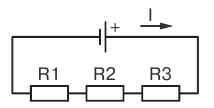 Рис 1. Последовательное соединение сопротивлений Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать: U = U1 + U2 + U3 где U1 = IR1 U2 = IR2 и U3 = IR3 или IR = IR1 + IR2 + IR3 Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3). Поделив теперь обе части равенства на I, будем окончательно иметь R = R1 + R2 + R3 Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков. Параллельное соединение сопротивлений Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением. 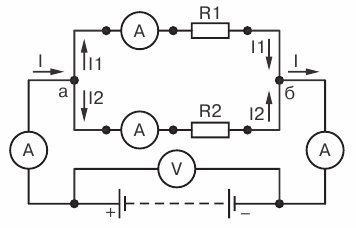 Рис 3. Параллельное соединение сопротивлений Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока. Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи. Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока. Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б). Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1, а во второй — I2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а). Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи. Рассмотрим теперь, каково будет соотношение между токами в ветвях. Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3, непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении. Это дает нам право написать, что U = U1 = U2, где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR. Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2, но так как U1 = U2, то и I1R1 = I2R2. Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви. Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь. Проводимость Способность тела (среды) проводить электрический ток, свойство тела или среды, определяющее возникновение в них электрического тока под воздействием электрического поля. Также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению. В Международной системе единиц (СИ) единицей измерения электрической проводимости является сименс (русское обозначение: См; международное: S), определяемый как 1 См = 1 Ом−1, то есть как электрическая проводимость участка электрической цепи сопротивлением 1 Ом. Виды электропроводимости: — Электронная проводимость, где переносчиками зарядов являются электроны. Такая проводимость характерна в первую очередь для металлов, но присутствует в той или иной степени практически в любых материалах. С увеличением температуры электронная проводимость снижается. — Ионная проводимость. Существует в газообразных и жидких средах, где имеются свободные ионы, которые также переносят заряды, перемещаясь по объёму среды под действием электромагнитного поля или другого внешнего воздействия. Используется в электролитах. С ростом температуры ионная проводимость увеличивается, поскольку образуется большее количество ионов с высокой энергией, а также снижается вязкость среды. — Дырочная проводимость. Эта проводимость обуславливается недостатком электронов в кристаллической решётке материала. Фактически, переносят заряд здесь опять же электроны, но они как бы движутся по решётке, занимая последовательно свободные места в ней, в отличии от физического перемещения электронов в металлах. Такой принцип используется в полупроводниках, наряду с электронной проводимостью. 3.8 Смешанное соединение в электрических цепях. Смешанным считают такое соединение, при котором в цепи существуют группы сопротивлений, включенных параллельно и последовательно. Если все сопротивления в этой схеме принимаются за одинаковые, то есть это выглядит таким образом: R1=R2=R3=R4=R5=R, а сопротивления R4 и R5 будут включенными параллельно, то сопротивление участка цепи cd определяется такой формулой: Rcd=R4*R5 / R4+R5= R / 2. 3.9 Принцип наложения. Основным свойством линейной электрической цепи является принцип наложения (принцип суперпозиции): реакция линейной электрической цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым из воздействий в отдельности. На этом принципе основан метод расчёта сложных цепей – метод наложения. Существо метода заключается в том, что в цепи, содержащей несколько источников, реакцию (искомый ток или напряжение) можно определить как сумму реакций, создаваемых каждым воздействием (источником) в отдельности, т.е. полагается, что каждый источник действует независимо. ЭЛЕКТРИЧЕСКИЕ КОНДЕНСАТОРЫ, ЁМКОСТЬ Электрическая емкость - свойство материальных объектов, в том числе специально для этого созданных, накапливать свободные электрические заряды и разделять связанные. Электрические конденсаторы - электротехнические элементы и устройства, предназначенные для выполнения функции электрической емкости в электрических цепях. Емкость конденсатора равна отношению абсолютной величины заряда на любой из двух его обкладок (напомним, что их заряды различаются только знаком) к разности потенциалов между обкладками: Емкость C измеряется в фарадах (Ф), если заряд Q выражен в кулонах (Кл), а разность потенциалов – в вольтах (В). Две только что упомянутые единицы измерения, вольт и фарада, названы так в честь ученых А. Вольты и М. Фарадея. Фарада оказалась настолько крупной единицей, что емкость большинства конденсаторов выражают в микрофарадах (10–6Ф) или пикофарадах (10–12Ф). 4.1 Последовательное и параллельное соединение конденсаторов. Последовательное соединение конденсаторов При таком соединении конденсаторы соединены последовательно друг за другом, то есть конец одного конденсатора соединяется с началом другого. Все конденсаторы принадлежат одному проводу, на котором нет разветвлений. Это приводит к тому, что через любой из конденсаторов протекает один и тот же ток, и если конденсаторы были первоначально не заряжены, то на них будет одинаковый заряд в любой момент времени. Общее напряжение на конденсаторах будет складываться из напряжений на каждом. |
