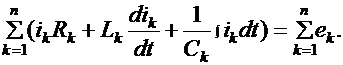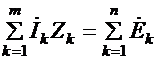Конспект лекций по дисциплине Электротехника и электроника
 Скачать 1.71 Mb.
|
|
Параллельное соединение конденсаторов При таком соединении конденсаторы соединены параллельно друг другу, то есть одни концы всех конденсаторов соединены в одну точку, а другие концы − в другую точку. Это приводит к тому, что на конденсаторах одинаковые напряжения, однако каждый конденсатор принадлежит своему проводу, поэтому на каждом из них свой заряд. ИНДУКТИВНОСТЬ. Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. В некоторых источниках её называют коэффициентом самоиндукции, так как она зависит от текущего в замкнутом контуре тока и создаваемого им магнитного потока. Для определения величины этого показателя применяют несколько вариантов расчёта, которые основываются на различных физических параметрах. 5.1 Магнитная индукция, как силовая характеристика магнитного поля. Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения. Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается. Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение. Магнитные поля, ориентированные в одном направлении, не нейтрализуют друг друга, а складываются, формируя единое поле. Формула магнитной индукции 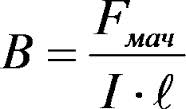 где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.5.2 Магнитный поток и потокосцепление Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности. Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как где — магнитный поток одного витка [ Вб ]. В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:
5.3 Закон электромагнитной индукции. Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.[1] или другими словами: Генерируемая ЭДС пропорциональна скорости изменения магнитного потока. При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца). 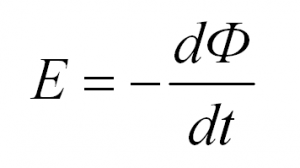 5.4 Индуктивность. Явление эл. магнитной индукции. Индуктивность – это элемент цепи, где происходит накопление энергии от магнитного поля. Так происходит запас поля или его преобразование в иные виды энергий. Самым идеальным примером служит катушка индуктивности. В ней происходит запасание поля и его дальнейшее преобразование в энергию других видов, в том числе и тепловую. Способность накапливать магнитное поле и является индуктивностью.  6. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА. 6.1 Синусоидальный ток и его основные характеристики. Синусоидальный ток представляет собой функцию времени. То есть в отличие от постоянного тока его значение меняется с течением времени. Основными характеристиками синусоидального тока являются. Амплитуда частота и начальная фаза. Частота f это количество колебаний в единицу времени. За единицу времени в системе СИ принимается одна секунда. Таким образом, количество колебаний за секунду это и есть частота синусоидального тока. И измеряется она в Герцах. Величина обратная частоте называется периодом колебания T=1/f (с). Определение периода звучит так период это время полного колебания. Если представить себе маятник часов, то период это время за которое он совершит движение из одного крайнего положения в другое и обратно. Начальная фаза синусоидального тока - это то время, на которое отстает либо опережает синусоида начальный момент времени. Представим две синусоиды одна, из которых начинается условно в нуле а другая в 1. То можно сказать, что вторая синусоида отстаёт по фазе от первой. Если обе синусоиды начинаются в одной точке то можно сказать что они синфазные, то есть имеют одну фазу. При этом они обе могут отставать от начального момента времени на одну и ту же величину, то есть иметь одинаковую начальную фазу. 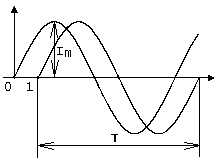 Математически синусоидальный ток описывается уравнением: i=Im*sin(wt+j) , где i - мгновенное значение тока это величина тока в определенный момент времени с учетом частоты и начальной фазы тока. Im - амплитуда тока. j - начальная фаза. w - угловая частота выражается как угловая частота -  Синусоидальный ток характеризуется амплитудой Im и периодом T. 6.2 Среднее и действующее значение синусоидального переменного тока   6.3 Коэффициенты амплитуды и формы. Отношение амплитудного значения тока (или напряжения) к действующему называется коэффициентом амплитуды: ;  Для синусоидальных функций Отношение действующего значения тока (или напряжения) к среднему по модулю называется коэффициентом формы:  ;  Определим коэффициент формы для синусоидальной функции тока: 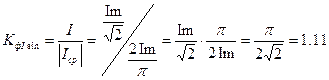 Для несинусоидальных периодических функций токов и напряжений и имеют другие значения. Смысл коэффициента амплитуды вполне понятен: он связывает между собой амплитудное и действующее значение периодической функции. Измеряя ток или напряжение прибором электромагнитной системы, мы получим действующее значение и через найдём амплитуду. Сняв осциллограмму функции тока или напряжения, легко определить её амплитуду и через найти действующее значение, необходимое для определения активной мощности. В чем смысл коэффициента формы? Дело в том, что приборы электромагнитной системы имеют низкую чувствительность и малую точность, а приборы магнитоэлектрической системы показывают только постоянную составляющую, которая у синусоидальных функций равна нулю (среднее значение функции за период). Однако если включить такой прибор через выпрямитель (диодный мост), то он будет показывать среднее по модулю значение функции, которое связано с действующим значением через . Очень часто детекторные приборы магнитоэлектрической системы градуируют в действующих значениях, хотя реагируют они на среднее по модулю значение. При этом используется (то есть прибор показывает 1А, а пишут 1.11А). Такой прибор правильно работает если им мерить синусоидальные функции, однако если форма тока будет несинусоидальной, то такой прибор будет давать заметную погрешность, обусловленную тем, что , а прибор отградуирован именно под это значение. При этом чем сильнее форма функции отличается от синусоидальной, тем больше погрешность. 6.4 Изображение синусоидально изменяющейся величины на комплексной плоскости Комплексная плоскость, на которой можно изобразить комплексные числа, дана на рис. 3.2. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости откладывают действительную часть комплексного числа, а по оси ординат - мнимую часть. На оси действительных значений ставим + 1, а на оси мнимых значений +j . Из курса математики известна формула Эйлера 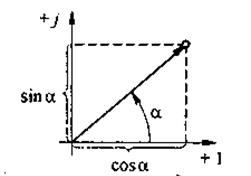 (3.8) Рисунок 3.2 Комплексное число eja изображают на комплексной плоскости вектором, численно равным единице и составляющим угол а с осью вещественных значений (осью +1). Угол а отсчитываем против часовой стрелки от оси + 1. Модуль функции  Проекция функции еja на ось + 1 равна cos a, a на ось +j равна sin a. Если вместо функции еja взять функцию Im еja, то  На комплексной плоскости эта функция, так же как и функция еja, изображается под углом a к оси + 1, но длина вектора будет в Iт раз больше. Угол α в формуле (3.8) может быть любым. Положим, что a = ωt + ψ, т. е. угол a изменяется прямо пропорционально времени. Тогда  (3.9)Слагаемое Im cos(ωt + ψ) представляет собой действительную часть (Re) выражения Iтеj(ωt + ψ)  (3.10)а функция Iт sin(ωt + ψ) есть коэффициент при мнимой части (lm) выражения Iтеj(ωt + ψ)  (3.11)Таким образом, синусоидально изменяющийся ток i ср. (3.1) и (3.11)) можно представить как lm Iтеj(ωt + ψ) или, что то же самое, как проекцию вращающегося вектора Iтеj(ωt + ψ) на ось +j (рис. 3.3). 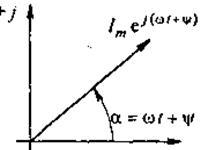 Рисунок 3.3 Исторически сложилось так, что в радиотехнической литературе за основу обычно принимают не синусоиду, а косинусоиду и потому пользуются формулой (3.10). С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени ωt=0. При этом вектор  (3.12)где - комплексная величина, модуль которой равен Iт; ψ - угол, под которым вектор проведен к оси + 1 на комплексной плоскости, равный начальной фазе. Величину называют комплексной амплитудой тока i. Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени ωt = 0. Точка, поставленная над током или напряжением , означает, что эта величина во времени изменяется синусоидально. Поясним сказанное. Пусть ток i = 8sin(ωt + 20°) А. Запишем выражение для комплексной амплитуды этого тока. В данном случае Im = 8 А, ψ = 20°. Следовательно, =8еj20° А. Пусть комплексная амплитуда тока = 25 е--j30° А. Запишем выражение для мгновенного значения этого тока. Для перехода от комплексной амплитуды к мгновенному значению умножим на еjωt и возьмем коэффициент при мнимой части от полученного произведения (см. формулу (3.11)):  Под комплексом действующего значения тока или комплексом тока (комплексным током) понимают частное от деления комплексной амплитуды на 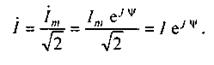 (3.13)6.5 Комплексные числа и действия над ними. Формула Эйлера. Уже простейшие алгебраические операции над действительными числами (извлечение квадратного корня из отрицательного числа, решение квадратного уравнения с отрицательным дискриминантом) выводят за пределы множества действительных чисел. Дальнейшее обобщение понятия числа приводит к комплексным числам. Замечательным свойством множества комплексных чисел является его замкнутость относительно основных математических операций. Иначе говоря, основные математические операции над комплексными числами не выводят из множества комплексных чисел. Комплексным числом (в алгебраической форме) называется выражение где – произвольные действительные числа, – мнимая единица, определяемая условием . Число называется действительной частью комплексного числа , обозначается (от латинского «realis»), число называется мнимой частью комплексного числа и обозначается (от латинского «imaginarius»). Два комплексных числа  и  равны тогда и только тогда, когда равны их действительные и мнимые части: , . Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).Комплексно-сопряженным к числу называется число . Очевидно, комплексно–сопряженное число к числу совпадает с числом : . Арифметические операции. Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры. Пусть , . Тогдасумма  ,разность  ,произведение  ,частное (при ) 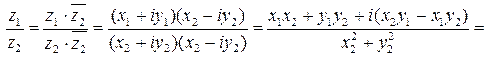 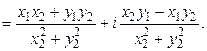 6.6 Сложение и вычитание синусоидальных функций на комплексной плоскости. Допусти, что нам необходимо сложить два тока (ix и i2) одинаковой частоты. Сумма их дает некоторый ток той же частоты: 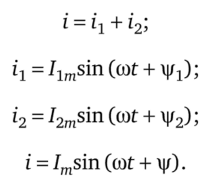 Требуется найти амплитуду 1т и начальную фазу |/ тока i. С этой целью ток i} изобразим на комплексной плоскости (рис. 3.4) вектором ilm = 11те№, а ток i2 — вектором i2m = I2meJV2- Геометрическая сумма векторов ilm и 12т даст комплексную амплитуду суммарного тока 1т = 1те™. Амплитуда тока 1т определяется длиной суммарного вектора, а начальная фаза |/ — утлом, образованным этим вектором и осью +1. 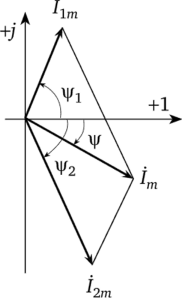 Рис. ЗА Для определения разности двух токов (ЭДС, напряжений) следует на комплексной плоскости произвести не сложение, а вычитание соответствующих векторов. Обратим внимание на то, что если бы векторы /1т, 12т и 7т стали вращаться вокруг начала координат с угловой скоростью со, то взаимное расположение векторов относительно друг друга осталось бы без изменений. 6.7 Мгновенная мощность. Предположим, что через участок электрической цепи (приемник энергии) под воздействием приложенного напряжения u проходит электрический заряд q. Совершаемая при этом элементарная работа или, что то же, поступающая в приемник элементарная энергия равна dw = udq = uidt. Производная энергии по времени, т.е. скорость поступления в цепь электрической энергии в данный момент времени, представляет собой мгновенную мощность. Следовательно, мгновенная мощность, поступающая в приемник, равна произведению мгновенных значений напряжения и тока 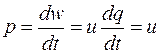 i.Мгновенная мощность p - величина алгебраическая; она положительна при одинаковых знаках u и i и отрицательна при разных знаках u и i. Если положительные направления для напряжения и тока приняты совпадающими, то при p > 0 энергия поступает в приемник, а при p < 0 энергия возвращается из рассматриваемого участка цепи обратно к источнику. Энергия, поступившая в приемник за промежуток времени от t1 до t2, выражается интегралом 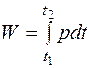 .В отличие от мгновенной мощности p, которая может иметь отрицательный или положительный знак, энергия, поступившая в приемник, всегда имеет положительный знак. В системе СИ работа и энергия измеряются в джоулях (Дж), мощность p - в ваттах (Вт). 6.8 Резистивный элемент в цепи синусоидального тока. Пусть имеется резистивный элемент r (рис. 3.6), по которому протекает синусоидальный ток  . Рисунок 3.6 – Резистивный элемент Согласно закону Ома на этом элементе возникает падение напряжения:  .Максимальные значения тока и напряжения связаны выражением: . Следовательно, действующие значения тока и напряжения также связаны выражением: . Из вышеизложенного следует, что напряжения и ток на резистивном элементе совпадают по фазе (рис. 3.7,а), т. е. имеет место совпадение максимальных значений в один момент времени. Это означает, что векторы действующих значений тока и напряжения направлены в одну сторону (рис. 3.7,б). На рисунке 3.7,а показаны кривые мгновенных значений тока и напряжения на резистивном элементе, на рисунке 3.8,б – векторная диаграмма токов и напряжения. 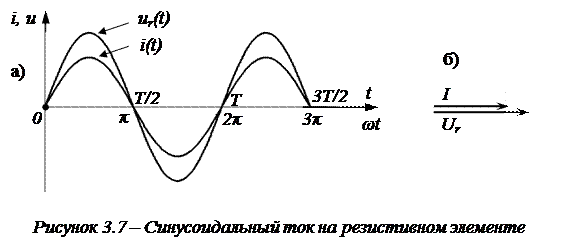 Мгновенная мощность определяется выражением . Среднее значение мощности за период равно:  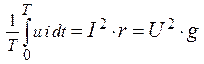 .Резистивный элемент называется активным сопротивлением, т.к. протекание синусоидального тока сопровождается потреблением активной мощности. 6.9 Индуктивный элемент в цепи синусоидального тока. Рассмотрим электрическую цепь, содержащую катушку, активное сопротивление которой настолько мало, что им можно пренебречь. Пусть ток в цепи с индуктивностью L(рис. 4,а) изменяется синусоидально: iL = Im sin t. Этот ток создает в катушке синусоидально изменяющийся магнитный поток, который наводит в ней ЭДС самоиндукции: eL= L d iL/dt. Напряжение источника u =uLуравновешивается ЭДС самоиндукцииeL: u = uL = – eL = L d iL / dt. Выполнив дифференцирование, получим uL = LImcost = LImsin(t + /2) = ULm sin(t + /2), где ULm=LIm, илиUL=LI. Произведение Lимеет размерность сопротивления, его обозначаютXLи называют индуктивным сопротивлением катушки. XL = L = 2f L, UL = XL I. +Сравнивая выражения для тока iL и напряженияuL,можно сделать вывод, чтона индуктивном элементе напряжение опережает по фазе ток на угол /2. Для цепи с индуктивностью закон Ома в комплексной форме записывается так:  .Учитывая фазовый сдвиг (=/2), для мгновенной мощности индуктивного элементаpLполучим: pL=uLiL= Umsin(t+/2)Imsin(t) = UmImcos(t)sin(t) = UIsin(2t). Мгновенная мощность pLимеет только переменную составляющую,частота которой в два раза превышает частоту напряжения (или тока) и представляет собой скорость прироста энергии магнитного поля индуктивности. За первую четверть периода тока, когдаuL иiL положительны, мгновенная мощностьpL 0. Это означает, что энергия поступает от источника и идет на увеличение энергии магнитного поля в индуктивной катушке (этот интервал времени отмечен знаком “+” на рис. 4,в). Во вторую четверть периода, когда токiLуменьшается от максимального значения до нуля, энергия магнитного поля отдается обратно источнику, при этом мгновенная мощность индуктивного элемента отрицательна (этот интервал времени отмечен знаком “–” на рис. 4,в.). Далее все повторяется. Следовательно, энергия периодически то забирается индуктивной катушкой от источника, то отдается ему обратно. Векторная диаграмма цепи с индуктивностью (рис. 4, а) изображена на рис. 4,б, а графики мгновенных значений тока, напряжения и мощности на рис. 4,в. 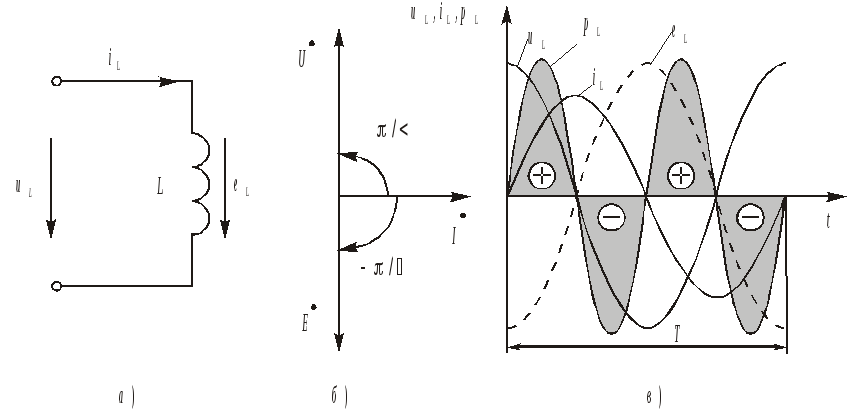 Рис. 4 6.10 Ёмкостной элемент в цепи синусоидального тока. Емкостный элемент — это идеализированный схемный элемент, позволяющий учесть протекание токов смещения и явление накопления энергии в электрическом поле реальных элементов электрической цепи. Его характеризует зависимость заряда q от напряжения и (кулон- вольтная характеристика) или емкость С = q/u. Графическое изображение емкостного элемента такое же, что и изображение конденсатора (рис. 3.7, а). Положительные направления отсчета и и i совпадают. Если приложенное к конденсатору напряжение и не изменяется во времени, то заряд q = Си на одной его обкладке и заряд на другой (С — емкость конденсатора) неизменны и ток через конденсатор не проходит (i = dq/dt = 0). Если же напряжение на конденсаторе изменяется во времени, например по синусоидальному закону (рис. 3.7, а):  то по синусоидальному закону будет меняться и заряд q конденсатора: q = Си = C[/msino)t, т. е. конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока: 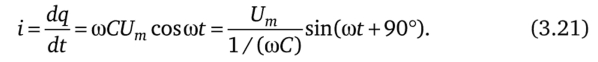 Из сопоставления (3.20) и (3.21) ясно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90°. Поэтому на векторной диаграмме (рис. 3.7, б) вектор im опережает вектор напряжения йт на 90°. Амплитуда тока 1т равна амплитуде напряжения Um, деленной на емкостное сопротивление:  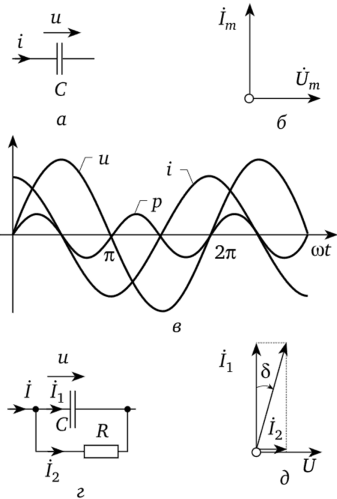 Рис. 3.7 Емкостное сопротивление обратно пропорционально частоте. Единица емкостного сопротивления — Ом. Графики мгновенных значений и, i, р изображены на рис. 3.7, в. Мгновенная мощность  За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем. Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода энергия снова запасается, за четвертую отдается и т. д. Если проинтегрировать по времени обе части равенства  то получим  Равенство (3.26) позволяет определить напряжение на конденсаторе через ток по конденсатору. Ток через реальный конденсатор, пластины которого разделены твердым или жидким диэлектриком, в котором имеются тепловые потери, обусловленные вязким трением дипольных молекул и другими причинами, в расчете можно учесть по схеме (рис. 3.7, г). Результирующий ток 7 = + /2. Ток опережает U на 90°, а ток /2 совпадает с U по фазе (рис. 3.7, д). Угол 8 называют углом потерь: tg8 = 1/QC, где Qc — добротность конденсатора, tg8 зависит от типа диэлектрика и от частоты и изменяется от нескольких секунд до нескольких градусов. 6.11 Основы символического метода расчёта цепей переменного тока Соединим последовательно лампу накаливания с сопротивлением R, батарею конденсаторов с емкостью С и катушку с большой индуктивностью L. Если данную цепь присоединить к зажимам генератора переменного тока, то лампа загорится, что свидетельствует о наличии электрического тока в цепи, несмотря на разрыв, существующий между изолированными друг от друга обкладками конденсатора. Для цепи переменного тока с последовательным соединением R, L, С (см. рисунок) дифференциальные уравнения по второму закону Кирхгофа имеют вид:  Здесь ток во всех трех участках один и тот же:  Разности потенциалов на всех трех сопротивлениях имеют вид: 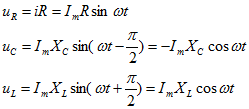 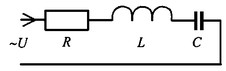 Решение системы дифференциальных уравнений можно существенно упростить, если перейти от дифференциальных уравнений к алгебраическим. Это можно сделать, изображая синусоидальные величины (i, u) в комплексной форме, т.е. в виде вектора на комплексной плоскости. 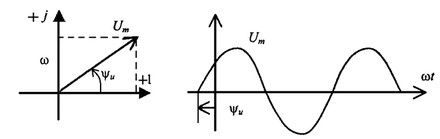 Вектор Um и его проекции. Расположим под углом относительно оси абсцисс вектор Um, длина которого в масштабе равна амплитуде изображаемой величины. Положительные углы будем откладывать в направлении против часовой стрелки. Проекции вектора на вертикальную ось мнимых величин в комплексной плоскости равны мгновенному значению напряжения. Система векторов на комплексной плоскости называется векторной диаграммой. Вектора вращаются относительно центра координат с одной и той же скоростью и поэтому относительно друг друга их положение не меняется. Векторная диаграмма изображается неподвижной в заданный момент времени, определяемый начальной фазой какой-либо величины, например, для идеальных элементов R, L, С. 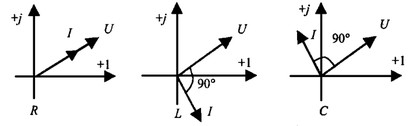 Векторные диаграммы для идеальных элементов R, L, C. Сложение двух функций в тригонометрической форме трудоемко, но легко производится в векторной форме. 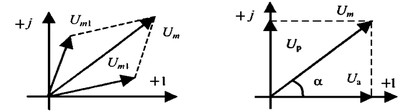 Векторные диаграммы сложения двух напряжений В расчетах применяют три формы записи комплексных величин: 1) алгебраическая  2) тригонометрическая  3) показательная, учитывая   Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повернута по отношению к вещественной на угол 90° в положительном направлении (против часовой стрелки). Переходы из одной формы записи в другие:  где   где  Представленная ранее система дифференциальных уравнений для цепи переменного тока с R, L, С в комплексном виде записывается следующим образом: 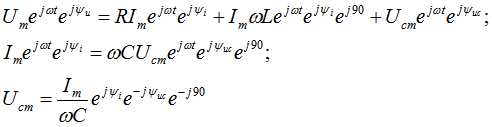 Используя выражения 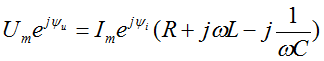 , запишем выражение для полного напряжения цепи: где  - комплексное сопротивление; - комплексная амплитуда напряжения; - комплексная амплитуда тока.При замене амплитудных значений на действующие получим закон Ома в комплексной форме:  Величину Z называют полным сопротивлением цепи переменного тока. Первый закон Кирхгофа в комплексной форме: 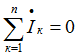 Второй закон Кирхгофа в комплексной форме: 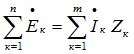 Векторная диаграмма напряжений для цепи с последовательным соединением R, L, C будет представлять собой прямоугольный треугольник. 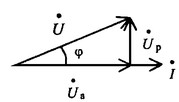 Треугольник напряжений 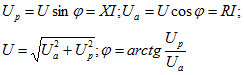 Треугольники токов, сопротивлений и мощностей строятся аналогично 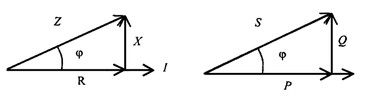    Полная мощность S = UI; активная мощность  реактивная мощность  где 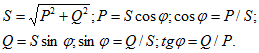 В треугольниках напряжений, токов, сопротивлений и мощностей угол сохраняет свое значение. При параллельном соединении ветвей их проводимости складываются в комплексной форме: 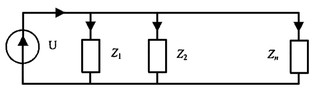 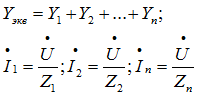 Общий ток, согласно первому закону Кирхгофа:  6.12 Комплексное сопротивление. Закон Ома для цепи синусоидального тока. Множитель R + jcoL—— в уравнении (3.32) представляет собой ком- шС плекс, имеет размерность сопротивления и обозначается числом Z. Его называют комплексным сопротивлением: 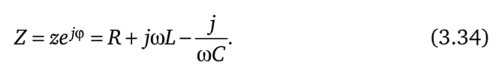 Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени. Уравнение (3.32) можно записать так:  Разделим обе его части на V2 и перейдем от комплексных амплитуд im и Ёт к комплексам действующих значений / и Ё:  Уравнение (3.35) представляет собой закон Ома для цепи синусоидального тока. В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jX:  где R — активное сопротивление; X — реактивное сопротивление. Для схемы рис. 3.9 реактивное сопротивление 6.13 Комплексная проводимость. Под комплексной проводимостью Y понимают величину, обратную комплексному сопротивлению Z: 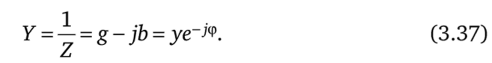 Единица комплексной проводимости — См (Ом-1). Действительную часть ее обозначают через g, мнимую — через Ъ. Так как 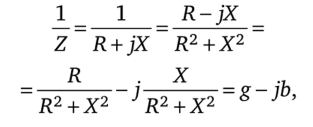 то 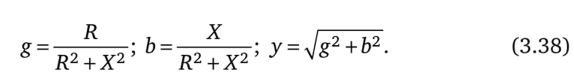 Если X положительно, то и b положительно. При X отрицательном b также отрицательно. При использовании комплексной проводимости закон Ома (3.35) записывают так:  или 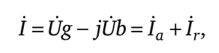 где ia — активная составляющая тока; 1Г — реактивная составляющая тока; U — напряжение на участке цепи, сопротивление которого равно Z. 6.14 Треугольник сопротивлений и проводимостей. Треугольник сопротивлений можно получить из векторной диаграммы цепи с последовательно соединенными участками активного, индуктивного и емкостного характера (рис. 3.4). 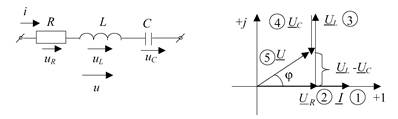 Рис. 3.4 Последовательность построения векторов указана в окружностях. Если все напряжения, составляющие векторную диаграмму, поделить на одну и ту же величину, очевидно, что получим такую же диаграмму, только в измененном масштабе. Если в качестве такой величины выбрать значение тока, который одинаков для всех элементов последовательной цепи, то получим соответствующие сопротивления. Учитывая, что сопротивления имеют скалярный характер, получим так называемый треугольник сопротивлений, где 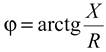 ;  (рис. 3.5).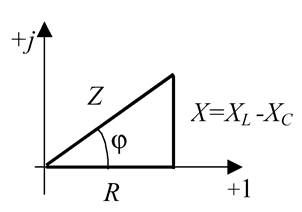 Рис. 3.5 Аналогично, рассматривая векторную диаграмму токов электрической цепи с параллельно соединенными активным, индуктивным и емкостным элементами (см. раздел 2.9), получим треугольник проводимостей (рис. 3.6) 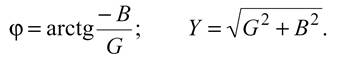  Рис. 3.6 6.15 Законы Кирхгофа в символической форме записи. Согласно первому закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:
Подставив вместо ik в (10.16)  и вынеся за знак суммы, получим  . Так как не равно нулю при любом t, то
Уравнение (10.16а) представляет собой первый закон Кирхгофа в символической форме записи. Пусть замкнутый контур содержит n ветвей и каждая k- ветвь в общем случае включает в себя источник ЭДС ek, резистор Rk, индуктивную катушку Lk и конденсатор Ck, по которым протекает ток ik. Тогда по второму закону Кирхгофа,
Но каждое слагаемое левой части можно заменить на , а каждое слагаемое правой части – на . Поэтому уравнение (10.17) переходит в
Уравнение (10.18) представляет собой второй закон Кирхгофа в символической форме записи. 6.16 Применение векторных диаграмм при расчёте цепей. Ток и напряжения на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма токов и напряжений. Аналитические расчеты электрических цепей синусоидального тока рекомендуется сопровождать построением векторных диаграмм, чтобы иметь возможность качественно контролировать эти расчеты. Качественный контроль заключается в сравнении направлений различных векторов на комплексной плоскости, которые получают при аналитическом расчете, с направлением этих векторов исходя из физических соображений. Например, на векторной диаграмме напряжение UL должно опережать ток / на 90°, а напряжение йс — отставать от тока / на 90°. Если аналитический расчет дает результаты, не совпадающие с такими очевидными положениями, то, следовательно, в него вкралась ошибка. Кроме того, векторную диаграмму часто используют и как средство расчета, например в методе пропорциональных величин. Пример 31 В схеме (рис. 3.13. а) е - 141sincot В; = 3 Ом; R2=2 Ом; L = 0,00955 Гн. Угловая частота со = 314 рад/с. Определить ток и напряжение на элементах цепи. 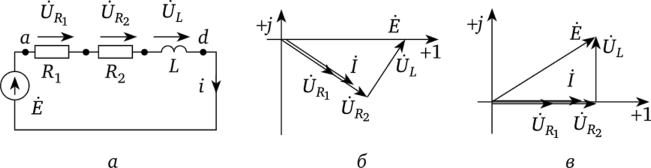 Рис. 3.13 Решение. Запишем уравнение для мгновенных значений: 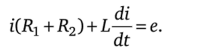 Перейдем от него к уравнению в комплексах:  где Z = Rl+R2 +;ooL = 3 + 2 +;314 • 0,00955 = 5 + 3j = 5,82е>31°. Комплекс действующего значения ЭДС Ё = 141/л/2=100В. Ток i-E/Z = 100/ (5,8е-'31°) = 17,2е^'31° А. Напряжения на URl-Uab = /Я1 =51,6е_-'31° В; на R2 UR2-Ubc-iR2 = = 34,4е->31° В, на L UL = Ucd = ;wL7 = 3; 17,2е->31° = 51,бе^ В. Векторная диаграмма изображена на рис. 3.13, б. Вектор Ё направлен по оси +1. Вектор тока / отстает от него на 31°. 6.17 Активная, реактивная и полная мощности. Треугольник мощностей. Нагрузка электрической цепи определяет, какой ток через неё проходит. Если ток постоянный, то эквивалентом нагрузки в большинстве случаев можно определить резистор определённого сопротивления. Тогда мощность рассчитывают по одной из формул: P=U*I P=I2*R P=U2/R По этой же формуле определяется полная мощность в цепи переменного тока. Нагрузку разделяют на два основных типа: Активную – это резистивная нагрузка, типа – ТЭНов, ламп накаливания и подобного. Реактивную – она бывает индуктивной (двигатели, катушки пускателей, соленоиды) и емкостной (конденсаторные установки и прочее). Последняя бывает только при переменном токе, например, в цепи синусоидального тока, именно такой есть у вас в розетках. В чем разница между активной и реактивной энергией мы расскажем далее простым языком, чтобы информация стала понятной для начинающих электриков. |
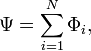Где — количество витков; — номер витка, с которым сцеплен поток 
