Конспект лекций по дисциплине Электротехника и электроника
 Скачать 1.71 Mb.
|
Смысл реактивной нагрузкиВ электрической цепи с реактивной нагрузки фаза тока и фаза напряжения не совпадают во времени. В зависимости от характера подключенного оборудования напряжение либо опережает ток (в индуктивности), либо отстаёт от него (в ёмкости). Для описания вопросов используют векторные диаграммы. Здесь одинаковое направление вектора напряжения и тока указывает на совпадение фаз. А если вектора изображены под некоторым углом, то это и есть опережение или отставание фазы соответствующего вектора (напряжения или тока). Давайте рассмотрим каждый из них. В индуктивности напряжение всегда опережает ток. «Расстояние» между фазами измеряется в градусах, что наглядно иллюстрируется на векторных диаграммах. Угол между векторами обозначается греческой буквой «Фи». 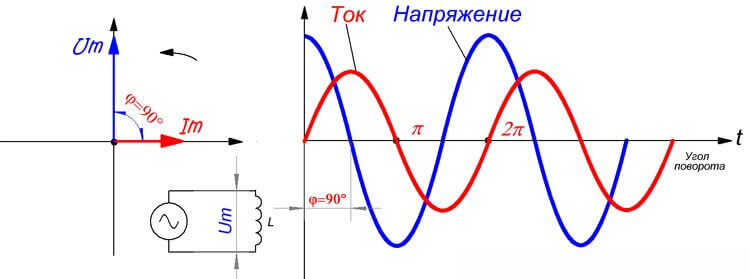 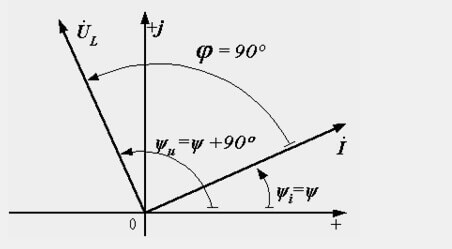 В идеализированной индуктивности угол сдвига фаз равен 90 градусов. Но в реальности это определяется полной нагрузкой в цепи, а в реальности не обходится без резистивной (активной) составляющей и паразитной (в этом случае) емкостной. В ёмкости ситуация противоположна – ток опережает напряжение, потому что индуктивность заряжаясь потребляет большой ток, который уменьшается по мере заряда. Хотя чаще говорят, что напряжение отстаёт от тока. 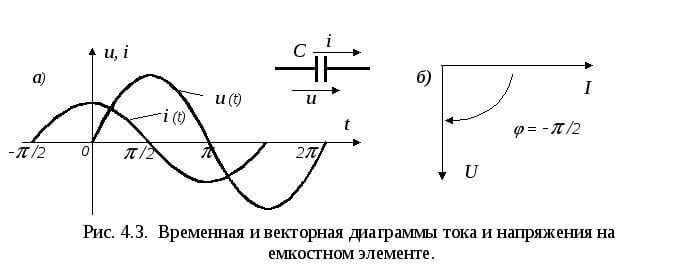 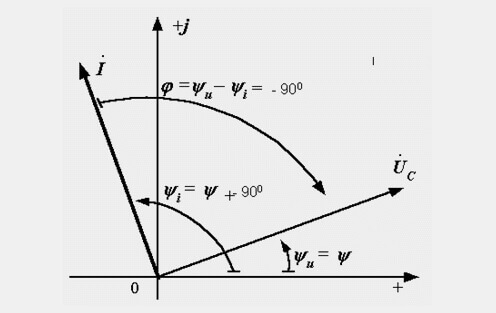 Если сказать кратко и понятно, то эти сдвиги можно объяснить законами коммутации, согласно которым в ёмкости напряжение не может изменится мгновенно, а в индуктивности – ток. Для измерения активной, реактивной и полной мощности, активной и реактивной энергии в прямом и обратном направлениях, а также других важных параметров сети могут использоваться многофукциональные измерительные приборы от компании EKF. Они достаточно легко монтируются и обслуживаются, к тому же могут настраиваться под любой трансформатор тока. Сам прибор дает возможность управления, анализа и оптимизации работы энергетического оборудования, систем и промышленных цепей. Треугольник мощностей и косинус ФиЕсли взять всю цепь, проанализировать её состав, фазы токов и напряжений, затем построить векторную диаграмму. После этого изобразить активную по горизонтальной оси, а реактивную – по вертикальной и соединить результирующим вектором концы этих векторов – получится треугольник мощностей. Он выражает отношение активной и реактивной мощности, а вектор, соединяющий концы двух предыдущих векторов – будет выражать полную мощность. Всё это звучит слишком сухо и запутано, поэтому посмотрите на рисунок ниже: 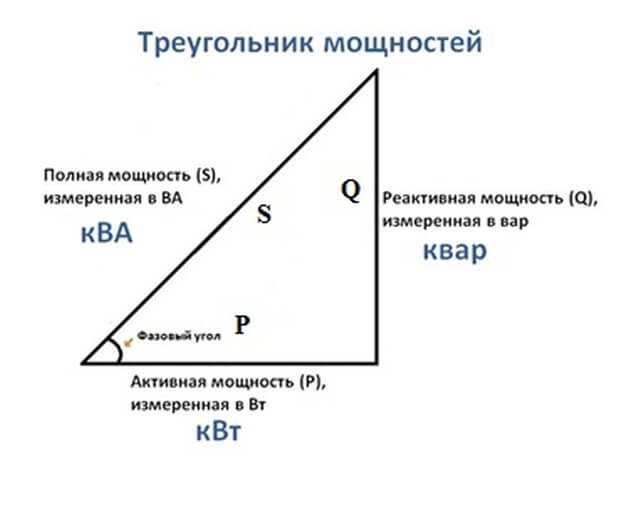 Буквой P – обозначена активная мощность, Q – реактивная, S – полная. Формула полной мощности имеет вид:  Самые внимательные читатели наверняка заметили подобие формулы теореме Пифагора. Единицы измерения: P – Вт, кВт (Ватты); Q – ВАр, кВАр (Вольт-амперы реактивные); S – ВА (Вольт-амперы); 6.18 Выражение мощности в комплексной форме записи. Широкое применение комплексного представления тока и напряжения в процессе анализа электрических цепей предполагает найти комплексное представление для активной, реактивной и полной мощности. На первый взгляд эта задача не должна вызывать затруднений. Достаточно в выражение для мощности подставить комплексные ток и напряжение. Посмотрим так ли это? Пусть заданы комплексные ток и напряжение . Тогда их произведение должно представлять полную мощность цепи.  Правая часть полученного выражения должна определять активную (действительную часть) и реактивную (мнимая часть) мощности. Но слагаемые правой части не соответствуют выражениям (4.16) и (4.21), так как в них сдвиг фаз определяется разностью Чтобы устранить такое несоответствие пользуются искусственным приемом. Под комплексным изображением полной мощности понимают произведение комплексного напряжения на комплексно-сопряженный ток. Напомним, что два комплексных числа и называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются только знаком:   При таком определении комплексная мощность цепи определится выражением  т.е. (4.27)Знак «тильда» означает комплекс полной мощности, составленный при участии сопряженного комплекса тока. Действительная часть комплексной мощности есть полная мощность, а мнимая часть - реактивная мощность. Модуль комплексного представления - полная мощность. 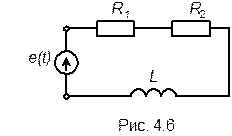 Рассмотрим пример. Пусть в схеме рис. (4.6) заданы ЭДС -  [B] и параметры элементов: R1=3[Ом]; R2=2[Ом]; L=0,0095[Г];  . Определить активную, реактивную и полную мощности цепи.Решение Комплекс действующего значения напряжения на входе всей схемы равен  Комплексное сопротивление цепи  Переходим к показательной форме комплексного сопротивления. Для этого находим модуль  и фазу  Отсюда Комплекс действующего значения тока  Сопряженный комплекс тока Комплекс мощности  Отсюда:    6.19 Двухполюсник в цепи синусоидального тока. Изображение разности потенциалов на комплексной Плоскости 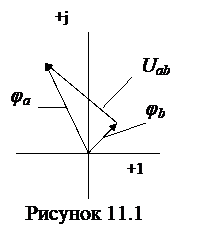 Потенциалы цепи синусоидального тока являются комплексными числами. Комплексное число на комплексной плоскости можно изобразить либо точкой, координаты которой равны действительной и мнимой частям комплексного потенциала, либо вектором, проведенным из начала координат к этой точке. Пусть  и  На комплексной плоскости (рис.11.1) представлены два вектора, изображающие эти комплексные потенциалы.
6.20 Резонанс токов. Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.  Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы. ПРИ КАКИХ УСЛОВИЯХ ВОЗНИКАЕТ Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация. В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C КАК ИСПОЛЬЗУЕТСЯ Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку. 6.21 Резонанс напряжений Резонансом напряжений называется режим электрической цепи синусоидального тока с последовательным соединенением резистивного R, индуктивноо L и емкостного С элементов, при котором угол сдвига фаз между общим напряжением (напряжением сети) и током в цепи равен нулю. Условием наступления резонанса напряженийявляется равенство индуктивного и емкостного сопротивлений цепи: XL = XC. (3.27) Электрическая цепь, питаемая синусоидальным переменным током, в которую входит конденсатор и катушка индуктивности называется колебательным контуром. Резонанс напряжений можно получить тремя способами: 1. Изменением частоты w синусоидального тока; 2. Изменением величин индуктивности или емкости колебательного контура, при котором меняются индуктивное XL или емкостное XC сопротивление; 3. При одновременном изменении параметров w, L, C цепи колебательного контура. Из условия резонанса напряжения (3.27) следует, что так как XL = wL и XC = 1/wC, то при резонансе напряжений  , (3.28)где wрез, рад/сек – резонансная частота. 7. ТРЁХФАЗНЫЕ ЦЕПИ. 7.1 Трёхфазная система ЭДС. Трехфазные электрические цепи представляют собой частный случай многофазных цепей. Многофазная система электрических цепей есть совокупность нескольких однофазных электрических цепей, в каждой из которых действуют синусоидальные ЭДС одной и той же частоты, создаваемые общим источником энергии и сдвинутые друг относительно друга по фазе на один и тот же угол. Термин «фаза» применяется для обозначения угла, характеризующего стадию периодического процесса, а также для названия однофазной цепи, входящей в многофазную цепь. Обычно применяют симметричные многофазные системы, у которых амплитудные значения ЭДС одинаковы, а фазы сдвинуты друг относительно друга на один и тот же угол 2π /m, где m — число фаз. Наиболее часто в электротехнике используют двухфазные, трехфазные, шестифазные цепи. В электроэнергетике наибольшее практическое значение имеют трехфазные системы. 7.2 Принцип работы 3-х фазного электромашинного генератора. Трехфазная система ЭДС, индуцируемых в статоре синхронного генератора, обычно представляет собой симметричную систему. На электрических схемах обмотки статора трехфазного генератора условно изображают так, как показано на рис. 2 (а). 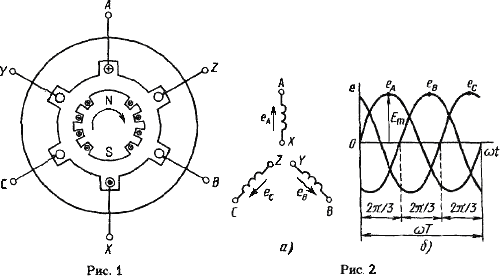 За условное положительное направление ЭДС в каждой фазе генератора принимают направление от конца к началу обмотки. 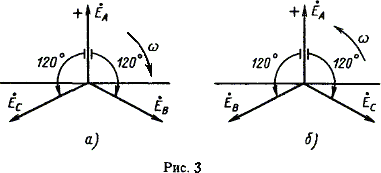 На рис. 3 (а, б) даны векторные диаграммы ЭДС трехфазного генератора для прямой и обратной последовательности чередования фаз. Последовательность, с которой ЭДС в фазных обмотках генератора принимает одинаковые значения, называют порядком чередования фаз или последовательностью фаз. Если ротор генератора вращать в направлении, указанном на рис. 1, то получается последовательность чередования фаз ABC, т. е. ЭДС фазы В отстает по фазе от ЭДС фазы А, и ЭДС фазы С отстает по фазе от ЭДС фазы В. Такую систему ЭДС называют системой прямой последовательности. Если изменить направление вращения ротора генератора на противоположное, то последовательность чередования фаз будет обратной. У генераторов роторы всегда вращаются в одном направлении, вследствие чего последовательность чередования фаз никогда не изменяется. 7.3 Расширение понятия фазы. Основные схемы соединения 3-х фазных цепей, определение линейных и фазных величин. Существует пять способов соединения трёхфазного генератора и трёхфазной нагрузки. Рассмотрим их все поочерёдно. Звезда – звезда с нулевым проводом (рис. 10) В этой схеме и обмотки генератора и нагрузки соединены звездой и имеется нулевой провод. 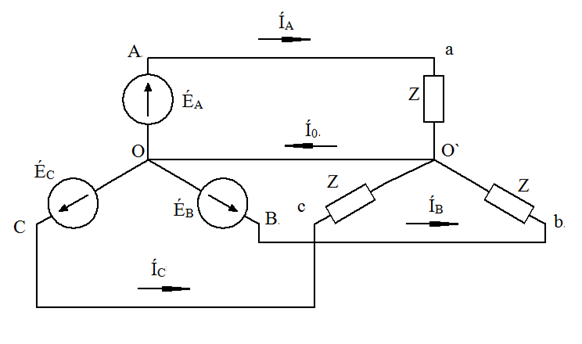 Рис. 10. Схема соединений звезда – звезда с нулевым проводом Рассмотрим все обозначения, принятые в трёхфазных цепях. Нулевой провод – провод, соединяющий нулевую точку генератора О и нулевую точку нагрузки О`. Ток текущий по нулевому проводу называют нулевым током и обозначают Í0. Линейный провод – провода, соединяющие точки А, В, С генератора и соответствующие точки а, b, с нагрузок. Токи, текущие по линейным проводам, называют линейными токами и обозначают ÍA, ÍB, ÍC. Положительное направление линейных токов всегда от генератора к нагрузке. Направление нулевого тока Í0 всегда от нагрузки к генератору. Модуль линейного тока обозначается IЛ, модуль тока нулевого провода I0. Зажимы А, В, С генератора не схеме всегда обозначается большими буквами, зажимы а, b, с нагрузок – маленькими. Между точками А и О, В и О, С и О – фазные ЭДС генератора Е́А, Е́В, Е́С соответственно. Между зажимами А, В, С – линейные ЭДС генератора Е́АВ, Е́ВС, Е́СА. Напряжение между точками а и о`, b и о`, с и о` называют фазными напряжениями нагрузки и обозначают ÚA, ÚB, ÚC. Модуль фазного напряжения обозначается Uф. Напряжения между точками а, b, с нагрузки, т. е. между линейными проводами в месте присоединения нагрузки, называется линейным напряжением нагрузки и обозначаются ÚAВ, ÚBС, ÚCА. Модуль линейного напряжения – UЛ. Каждую из трёх обмоток генератора называют фазой генератора, каждую из трёх нагрузок – фазой нагрузки. Токи, протекающие по фазам генератора, называют фазовыми токами генератора. Токи, протекающие по фазам нагрузки, называют фазовыми токами нагрузки. Модуль фазового тока обозначается Iф. Нагрузка называется равномерной или симметричной, когда во всех фазах включена одинаковая нагрузка по величине и по характеру. Для генератора и равномерной нагрузки справедлива векторная диаграмма рис. 11. 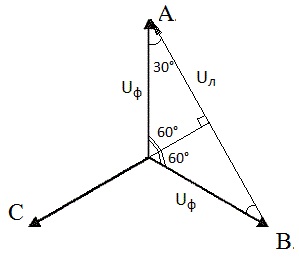 Рис. 11. Векторная диаграмма    (3)Для данной схемы соединения звезда – звезда с нулевым проводом в фазах генератора и нагрузки течёт тот же ток, что и в линейном проводе. Отдельно запишем соотношение между линейными и фазными величинами для генератора и нагрузки. Для генератора: (4) (5)Для нагрузки: (6) (7) |
изобразится вектором, направленным от b к a. Первый индекс у напряжения указывает, к какой точке следует направить стрелку вектора напряжения. Естественно, что 