Конспект лекций по дисциплине Электротехника и электроника
 Скачать 1.71 Mb.
|
|
Звезда – звезда без нулевого провода (рис. 12) 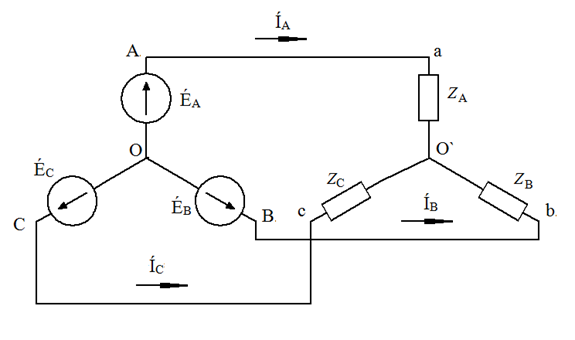 Рис. 12. Схема соединений звезда – звезда без нулевого провода Для генератора: (8)  (9)Для нагрузки: (10) (11)Звезда – треугольник (рис. 13) В данной схеме обмотки генератора включены звездой, а нагрузки треугольником. В этой схеме кроме линейных токов нагрузок ÍA, ÍB, ÍC появляются фазные токи нагрузок Íab, Íbc, Íca, протекающие по треугольнику нагрузок. 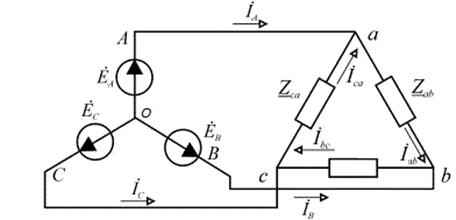 Рис. 13. Схема соединения звезда - треугольник При равномерной нагрузке фазные токи нагрузок Íab, Íbc, Íca образуют равносторонний треугольник (рис. 14): 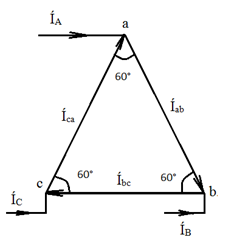 Рис. 14. Фазные токи нагрузок Для узлов а, b, с по первому закону Кирхгофа можно записать: ÍA = Íab - Íca; (12) ÍB = Íbc - Íab; (13) ÍC = Íca - Íbc; (14) Изобразим векторную диаграмму согласно выражению (12), т. е. сложим вектор Íab с вектором - Íca, что показано на рис. 15. Сумма этих векторов равна линейному току ÍA. 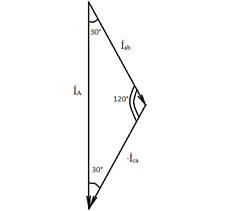 Рис. 15. Векторная диаграмма Между фазными токами нагрузок Íab, Íbc, Íca при равномерной нагрузке углы 120°. На векторной диаграмме фазные токи Íab, Íbc и линейный ток ÍA образуют равнобедренный треугольник, в котором углы между фазными токами нагрузок и линейным током равны 30°. Это справедливо и для выражений (13) и (14). Тогда можно обобщить (рис. 16): 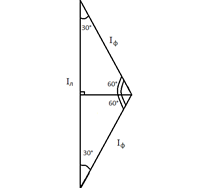 Рис. 16. Соотношение между линейным и фазным токами Для рис. 16 можно записать:    (15)Таким образом для схемы звезда – треугольник при равномерной нагрузке соответствия между линейными и фазными величинами выглядят следующим образом: Для генератора: (16)(17) Для нагрузки: (18)(19) Треугольник – треугольник (рис. 17) 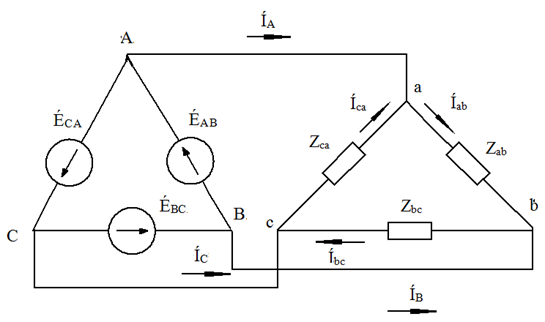 Рис. 17. Схема соединений треугольник - треугольник При равномерной нагрузке соотношения между линейными и фазными величинами выглядят следующим образом: Для генератора: (20)(21) Для нагрузки: (22)(23) Треугольник – звезда (рис. 18) При равномерной нагрузке соотношения между линейными и фазными величинами выглядит: 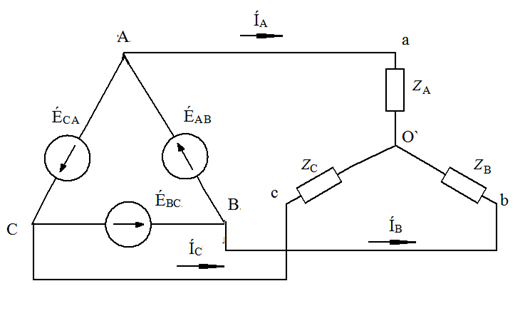 Рис. 18. Схема соединения треугольник - звезда Для генератора: (24)(25) Для нагрузки: (26) (27)Выше рассмотренные соотношения между линейными и фазными величинами всегда соблюдаются для генератора при любой нагрузке равномерной или неравномерной. Рассмотренные соотношения между линейными и фазными величинами для нагрузки соблюдаются только в случае равномерной нагрузки. 7.4 Соотношения между линейными и фазными токами и напряжениями для различных схем соединения. При соединении фаз по схеме «звезда» линейное напряжение по модулю в 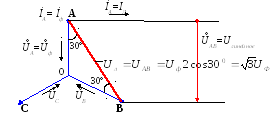 раз больше фазного напряжения, что следует из рисунка 4.7. Рисунок 4.7 – Соотношение между фазными и линейными токами при соединении обмоток по схеме «звезда» В соответствии с этим, в четырехпроводной трехфазной цепи имеются два уровня напряжения, различающиеся в раз (380/220 и 220/127), что позволяет использовать приемники с различным номинальным напряжением.+Так как обмотка генератора, линейный провод и приемник, принадлежащие одной фазе, соединяются последовательно, то при соединении генератора «звездой» линейный ток равен фазному току IЛ=Iф. Комплексные величины линейных и фазных токов обозначаются İA, İB, İC. Ток в нейтральном проводе определяется по первому закону Кирхгофа:
Таким образом, ток в нейтральном проводе равен геометрической сумме фазных токов. При возникновении несимметрии токов в фазах нагрузки по нейтральному проводу протекает ток i0, амплитуда которого меньше амплитуды токов в линейных проводах. В соответствии с этим сечение нулевого провода принимают на ступень меньше сечения линейных проводов. В симметричной трехфазной системе при соединении фаз по схеме «звезда» действующие фазные и линейные токи равны друг другу, а линейное напряжение в раз больше фазного. Обмотки трехфазных генераторов на электростанциях всегда соединяют «звездой», что позволяет выполнять изоляцию обмоток на фазное напряжение.При соединении фаз по схеме «треугольник» напряжение между началом и концом фазы – это напряжение между линейными проводами. В симметричной трехфазной системе при соединении фаз нагрузки «треугольником» фазные и линейные напряжения равны друг другу, а линейный ток в 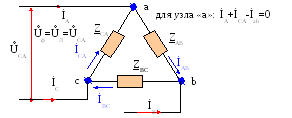раз больше фазного. Рисунок 4.8– Соотношение между фазными и линейными токами при соединении по схеме «треугольник» Преимуществом соединения фаз приемника «треугольником» является взаимная независимость фазных токов. Таблица 4.1 – Соотношения между фазными и линейными токами и напряжениями при различном соединении фаз для симметричной трехфазной цепи
7.5 Преимущества 3-х фазных систем. 1. При одинаковых напряжениях и мощностях потребителей и прочих равных условиях питание трехфазным током позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными линиями. 2. При прочих равных условиях трехфазный генератор дешевле, легче и экономичнее, чем три однофазных генератора такой же суммарной мощностью. То же самое относится к трехфазным двигателям и трансформаторам. 3. Трехфазная система токов позволяет получить вращающееся магнитное поле с помощью трех неподвижных катушек. 4. При равномерной нагрузке трехфазный генератор создает на валу приводного двигателя постоянный момент, в отличии от однофазного генератора, у которого мощность и момент пульсируют с двойной частотой тока. 7.6 Поворотный оператор а. При симметричной трехфазной системе обмоток обобщенный вектор тока можно представить в виде
+где  – операторы поворота, аia, ib и ic – мгновенные значения токов соответствующих обмоток.Оператор поворота вектора – множитель вектора, означающий поворот этого вектора на угол . Обозначение вектора строчным символом принято для указания на то, что его координаты являются функциями времени аналогично тому, как строчные символы при обозначении скалярных величин указывают на мгновенное значение. +При таком представлении фазные токи ia, ib и ic можно рассматривать как проекции вектора i на соответствующие оси фазных обмоток (рис. 1.1 а)). Если произвести построение вектора i , откладывая значения фазных токов ia, ib и ic на осях обмоток (рис. 1.1 б)), то суммарный вектор окажется в полтора раза больше того вектора, проекции которого соответствуют фазным токам. Поэтому в выражении (1.1.1)присутствует коэффициент 2/3, приводящий модуль суммарного вектора к такому значению, которое при проецировании на оси фазных обмоток даст истинные значения фазных токов. 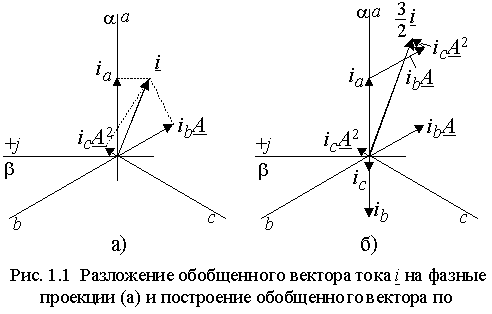 Если статор машины имеет нулевой провод, то фазные токи могут содержать нулевую составляющую и их значения можно представить в виде ia+io, ib+io и ic+io. Тогда вектор тока будет равен 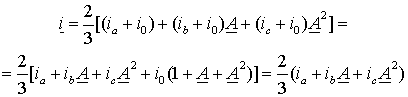 Таким образом, обобщенный вектор тока статора не содержит нулевой составляющей и ее при анализе следует учитывать особо. 7.7 Активная, реактивная и полная мощности 3-х фазной системы. Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз приемника.  В симметричной трехфазной системе (при симметричном генераторе и приемнике) при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковы. Для каждой из фаз справедливо выражение  ,где - φ угол сдвига фаз между фазными напряжением и током. Активная мощность системы в этом случае Заменив действующее значение фазных тока и напряжения линейными при соединении источника энергии и приемника по схеме звезда т треугольник, получим одно и то же выражение для активной мощности симметричной трехфазной системы:  В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметричной трехфазной системы  ,или после замены действующих значений фазных тока и напряжения линейными  .7.8 Получение вращающегося магнитного поля. Условия получения: 1. наличие не менее двух обмоток; 2. токи в обмотках должны отличаться по фазе 3. оси обмоток должны быть смещены в пространстве. В трёхфазной машине при одной паре полюсов (р=1) оси обмоток должны быть смещены в пространстве на угол 120°, при двух парах полюсов (р=2) оси обмоток должны быть смещены в пространстве на угол 60° и т.д. Рассмотрим магнитное поле, которое создаётся с помощью трёхфазной обмотки, имеющей одну пару полюсов (р=1) (рис. 5.7). Оси обмоток фаз смещены в пространстве на угол 120° и создаваемые ими магнитные индукции отдельных фаз (BA, BB, BC) смещены в пространстве тоже на угол 120°. Магнитные индукции полей, создаваемые каждой фазой, как и напряжения, подведённые к этим фазам, являются синусоидальными и отличаются по фазе на угол 120°. Приняв начальную фазу индукции в фазе А (φA) равной нулю, можно записать: 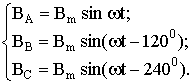 Магнитная индукция результирующего магнитного поля определяется векторной суммой этих трёх магнитных индукций. . Найдём результирующую магнитную индукцию (рис. 2.8) с помощью векторных диаграмм, построив их для нескольких моментов времени.
7.9 Принцип работы асинхронного двигателя. При подаче к обмотке статора напряжения, в каждой фазе создаётся магнитный поток, который изменяется с частотой подаваемого напряжения. Эти магнитные потоки сдвинуты относительно друг друга на 120°, как во времени, так и в пространстве. Результирующий магнитный поток оказывается при этом вращающимся. Результирующий магнитный поток статора вращается и тем самым создаёт в проводниках ротора ЭДС. Так как обмотка ротора, имеет замкнутую электрическую цепь, в ней возникает ток, который в свою очередь взаимодействуя с магнитным потоком статора, создаёт пусковой момент двигателя, стремящийся повернуть ротор в направлении вращения магнитного поля статора. Когда он достигает значения, тормозного момента ротора, а затем превышает его, ротор начинает вращаться. При этом возникает так называемое скольжение. Скольжение s - это величина, которая показывает, насколько синхронная частота n1 магнитного поля статора больше, чем частота вращения ротора n2, в процентном соотношении. 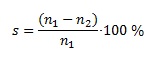 Скольжение это крайне важная величина. В начальный момент времени она равна единице, но по мере возрастания частоты вращения n2 ротора относительная разность частот n1-n2 становится меньше, вследствие чего уменьшаются ЭДС и ток в проводниках ротора, что влечёт за собой уменьшение вращающего момента. В режиме холостого хода, когда двигатель работает без нагрузки на валу, скольжение минимально, но с увеличением статического момента, оно возрастает до величины sкр - критического скольжения. Если двигатель превысит это значение, то может произойти так называемое опрокидывание двигателя, и привести в последствии к его нестабильной работе. Значения скольжения лежит в диапазоне от 0 до 1, для асинхронных двигателей общего назначения оно составляет в номинальном режиме - 1 - 8 %. Как только наступит равновесие между электромагнитным моментом, вызывающим вращение ротора и тормозным моментом создаваемым нагрузкой на валу двигателя процессы изменения величин прекратятся. Выходит, что принцип работы асинхронного двигателя заключается во взаимодействии вращающегося магнитного поля статора и токов, которые наводятся этим магнитным полем в роторе. Причём вращающий момент может возникнуть только в том случае, если существует разность частот вращения магнитных полей. |
