Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика

• Название: Конспект лекций по дисциплине Компьютерная графика
• Анкор: Конспект лекций по компьютерной графике.doc
• Дата: 22.04.2017
• Размер: 16.3 Mb.
• Имя файла: Конспект лекций по компьютерной графике.doc
• Тип: Конспект лекций; #5372
• страница: 14 из 46

4.4 Математические основы векторной графики

Если основным элементом растровой графики является пиксел (точка), то в слу­чае векторной графики в роли базового элемента выступает линия. Это связано с тем, что в векторной графике любой объект состоит из набора линий, соединен­ных между собой узлами. Как уже отмечалось в предыдущем разделе, отдельная линия, соединяющая соседние узлы, называется сегментом (в геометрии ей соответствует отрезок). Сегмент может быть задан с помощью уравнения прямой или уравнения кривой линии, требующих для своего описания разного количества па­раметров. Для более полного понимания механизма формирования векторных объектов рассмотрим способы представления основных элементов векторной гра­фики: точки, прямой линии, отрезка прямой, кривой второго порядка, кривой тре­тьего порядка, кривых Безъе.

В векторной графике тачке соответствует узел. На плоскости этот объект пред­ставляется двумя числами (X, Y), задающими его положение относительно нача­ла координат.

Для описания прямой линии используется уравнение Y = аХ + b. Поэтому для по­строения данного объекта требуется задание всего двух параметров: а иb. Резуль­татом будет построение бесконечной прямой в декартовых координатах. В отличие от прямой, отрезок прямой требует для своего описания двух допол­нительных параметров, соответствующих началу и концу отрезка (например, X₁ и Х₂).

К классу кривых второго порядка относятся параболы, гиперболы, эллипсы и окруж­ности, то есть все линии, уравнения которых содержат переменные в степени не выше второй. В векторной графике эти кривые используется для построения базо­вых форм (примитивов) в виде эллипсов и окружностей. Кривые второго порядка не имеют точек перегиба. Используемое для описания этих кривых каноническое уравнение требует для своего задания пяти параметров:

х² + a1y² + а₂ху + а₃х + а₄у + a₅ = 0.

Для построения отрезка кривой требуется задать два дополнительных параметра.

В отличие от кривых второго порядка кривые третьего порядка могут иметь точку перегиба. Например, график функции Y ™ X³ (рис. 10.6) имеет точку перегиба в начале координат (0, 0). Именно эта особенность данного класса функций позво­ляет использовать их в качестве основных кривых для моделирования различных природных объектов в векторной графике. Следует отметить, что упомянутые ра­нее прямые и кривые второго порядка являются частным случаем кривых третье­го порядка.

Каноническое уравнение, используемое для описания уравнения третьего поряд­ка, требует для своего задания девяти параметров:

х³ + a₁y³ + a₂ х² у+ а₃ху² + а₄х² + а₅у² + а₆ху + а₇х + а₈у + а₉ = 0.

Для описания отрезка кривой третьего порядка требуется на два параметра больше. Кривые Безъе — это частный вид кривых третьего порядка, требующий для своего описания меньшего количества параметров — восьми вместо одиннадцати. В ос­нове построения кривых Безье лежит использование двух касательных, проведен­ных к крайним точкам отрезка линии (рис. 4.6, справа). На кривизну (форму) линии влияет угол наклона и длина отрезка касательной, значениями которых можно управлять в интерактивном режиме путем перетаскивания их концевых точек. Таким образом, касательные выполняют функции виртуальных рычагов, позволяющих управлять формой кривой. Более подробно об этом будет сказано далее в разделе «Кривые Безье».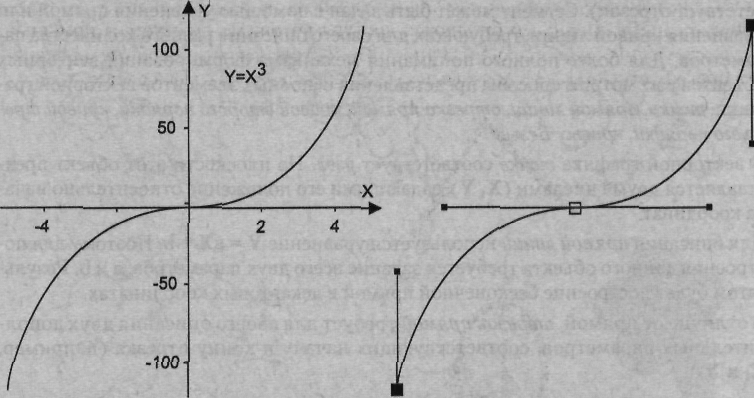



Рис. 4.6. Представление кривой линии с помощью кривых третьего порядка: слева — классический вариант; справа — кривая Беэье

4.5. Элементы (объекты) векторной графики

Теперь давайте познакомимся более детально с основными элементами векторно­го рисунка, рассмотренными нами ранее в разделе «Структура векторной иллюст­рации».
Линии

Как уже отмечалось, в основе векторной графики лежит использование математи­ческих представлений о свойствах контуров, основу которых составляет элемен­тарный объект векторной графики линия. С ее помощью можно легко построить любой более сложный объект. Например, объект четырехугольник можно создать с помощью четырех линий, а куб — с помощью 12 линий или 6 четырехугольников. Таким образом, иллюстрация составляется из простых объектов, как из кубиков.

Благодаря этому процесс рисования а векторных редакторах фактически сводит­ся к созданию контуров (объектов) нужной формы и приданию им определенных заливок и обводок. Этот принцип лежит в основе всех программ векторной графи­ки. Различаются лишь приемы работы и некоторые специальные эффекты.

В то же время построение линии наряду с использованием для ее описания математи­ческого аппарата предполагает задание ряда дополнительных атрибутов, определяю­щих ее основные свойства: форму, толщину, цвет, стиль (сплошная, пунктирная и т. п.). Количество перечисленных атрибутов зависит от вида линии. Открытые линии, напри­мер, в отличие от замкнутых не имеют атрибута заливки (рис. 4.7). Замкнутые кон­туры кроме обводки могут иметь определенную пользователем заливку).

По умолчанию контуры объектов обычно не имеют толщины. Чтобы контур был виден на экране, ему придают обводку (абрис) опре­деленной толщины, стиля (например, сплошная или пунктирная) и цвета. В большинстве редакторов выбор перечисленных атрибутов линии выполняется путем использования специальных библиотек, доступ к которым реализуется с помощью соответствующих окон диалога. На рис. 4.8 - 4,9 приведены подобные окна диа­лога программы Corel XARA, называемые Галерея линии и Галерея цветов.





Рис. 4.7. Иллюстрация свойств векторного объекта Линия: 1) прямолинейный незамкнутый контур (линия), нарисованный в программе Corel XARA 2 инструментом Рисунок от руки (Freehand) при нажатой клавише Alt без атрибута обводки (слева) и с добавлением обводки (справа) толщиной 4 пункта (4pt); 2) замкнутая линия в виде эллипса без заливки (слева) и с заливкой(справа)

Более подробно цветовые и другие параметры объектов будут рассмотрены далее в разделе «Атрибуты объекта — заливка и обводка».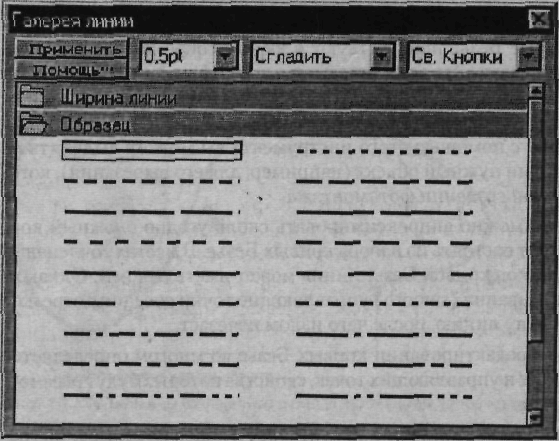



Рис. 4.8. Часть окна диалога Галерей линии Corel XARA с открытой папкой Образец, где можно выбрать любой из имеющихся в ней стилей линии — сплошная, пунктирная и т. п.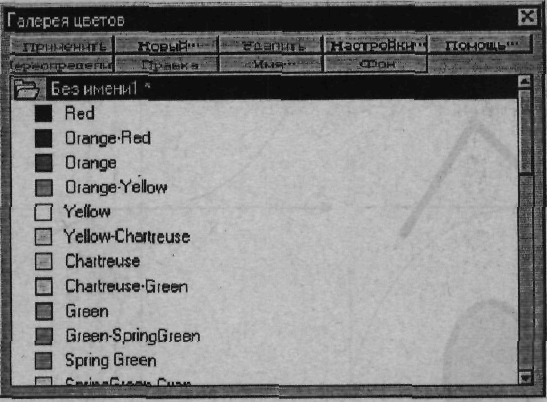


Рис. 4.9. Доступ к цветовым атрибутам линии в Corel XARA предоставляется в окне диалога Галерея цветов
Кривые Безье

В начале 70-х годов профессор Пьер Безье, проектируя на компьютере корпуса автомобилей «Рено», впервые применил для этой цели особый вид кривых, опи­сываемых уравнением третьего порядка, которые впоследствии стали известными под названием кривые Безье (функция Bezier).

Поскольку эти линии имеют особое значение как для векторной, так и растровой графики, имеет смысл рассмотреть их более подробно.

В настоящее время кривые Безье присутствуют в любом современном графиче­ском пакете. Достаточно сказать, что все компьютерные шрифты состоят из кривых Безье. Кривые Безье находят также широкое применение и в растровой графике. Так, в программе Photoshop используется термин контур (path), базирующийся на кривых Безье. Именно с помощью этого инструмента вы можете выделить на сканированной фотографии нужный объект (например, для его вырезания), кото­рый будет использован при создании фотомонтажа.

Отрезками такой кривой можно аппроксимировать сколь угодно сложный кон­тур. В этом случае он будет состоять из набора кривых Безье. В местах сочленений сформированная из отрезков кривой Безье линия может иметь изломы. Однако с помощью функции сглаживания (smooth) управляющие точки соседних отрезков легко выстраиваются в одну линию, после чего излом исчезает. Гибкость в построении и редактировании кривых Безье во многом определяется характеристиками узловых и управляющих точек, свойства которых будут рассмот­рены в следующем разделе.

Появление кривых Безье вызвало настоящий переворот в видео и трехмерной гра­фике. Это связано с тем, что до появления формул Безье контуры компьютерных персонажей были ломаными, поверхности — гранеными, а движение — прерывистым, скачкообразным, неестественным. Использование кривых Безье позволило реализовать наиболее общий и интуитивно понятный способ управления движе­нием. В соответствии с ним параметрам кривой можно поставить в соответствие параметры движения компьютерного персонажа. В результате движение будет про­исходить по тем же рассмотренным нами правилам. Таким образом, знаменитая кривая используется не только в двухмерной компьютерной графике, но и в трех­мерной графике, видео и анимаций.

Узлы (Опорные точки)

Наряду с линией (line) другим основным элементом векторной графики является узел (опорная точка). Как уже отмечалось, линии и узлы используются для по­строения контуров, которые могут быть представлены в виде прямой, кривой или формы. Каждый контур имеет несколько узлов.

В векторных редакторах (как, впрочем, и в растровых) форму контура изменя­ют путем манипуляции узлами. Это можно сделать одним из следующих спо­собов:

• 
  перемещением узлов;
  

• 
  изменением свойств узлов (в том числе атрибутов связанных с ними касательных линий и управляющих точек, рис. 4.10);
  

• 
  добавлением или удалением узлов.
  

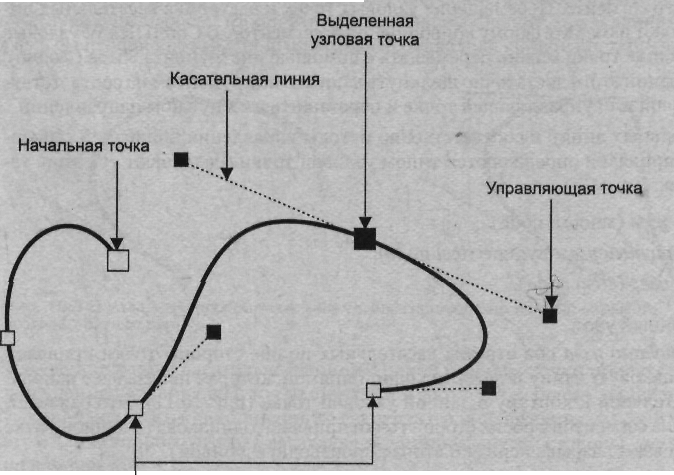Рис. 4.10. Невыделенные узловые точки
Таким образом, в основе всех процедур, связанных с редактированием (отчасти и созданием) любого типа контуров, лежит работа с узлами. Поэтому прежде, чем приступить к изучению процедур редактирования, давайте сначала познакомимся с типами узловых точек.

Касательные линии и управляющие точки

При выделении узловой точки криволинейного сегмента у нее появляются одна или две управляющие точки, соединенные с узловой точкой касательными линия­ми, Управляющие точки изображаются черными закрашенными точками. Распо­ложение касательных линий и управляющих точек определяет длину и форму (кри­визну) криволинейного сегмента, а их перемещение приводит к изменению формы контура.

Б локализованных версиях векторных программ наряду с термином касательные используются и другие термины: рычаги управления, направляющие и «.усы». Фор­ма и цвет управляющих точек также зависят от используемого редактора. Если в CorelDRAW они, как и выделенные узлы, обозначаются черными квадратиками, но меньшего размера, то в Corel XARA они закрашены красным цветом, а выде­ленный узел отображается незакрашенным квадратом.

Типы узловых точек

Касательная линия всегда является касательной к сегменту кривой в узловой точ­ке. Ее наклон и длина определяют наклон и радиус изгиба соответствующего кри­волинейного сегмента. Перемещение узловых точек и настройка касательных ли­ний позволяют изменять форму криволинейных сегментов. Различают три типа уз­ловых точек:

• 
  гладкий узел (smooth node);
  
• 
  симметричный узел (symmetrical node);
  
• 
  острый узел (cusp node).
  

Симметричный узел

У симметричного узла оба отрезка касательных по обе стороны точки привязки имеют одинаковую длину и лежат на одной прямой, которая показывает направ­ление касательной к контуру в данной узловой точке (рис. 4.11). Это означает, что кривизна сегментов с обеих сторон точки привязки одинакова (в данной точке не претерпевают разрыва первая и вторая производные кривой).

Изменение положения управляющей точки приводит к соответствующему изме­нению угла наклона касательной к кривой. Изменение длины касательной линии с одной стороны точки привязки путем перемещения управляющей точки приво­дит к соответствующему изменению и второй касательной линии, что изменяет радиус кривизны линии в точке привязки.

В CorelDRAW симметричные узлы создаются автоматически при рисовании кривых инструментом Bezier (Кривая Безье) методом перетаскивания. Поскольку этот тип уз­лов является частным случаем гладких узлов в большинстве программ векторной гра­фики (например, в Corel Хата), он не выделен в виде самостоятельного типа узла.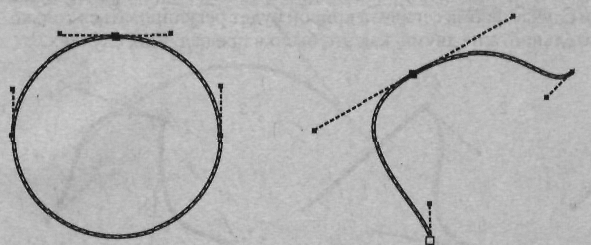



Рис. 4.11. У симметричной узловой точки длина обоих отрезков касательных одинакова, и они лежат на одной прямой

Гладкий узел

У гадкой узловой точки оба отрезка касательных линий по обе стороны точки при­вязки лежат на одной прямой, которая показывает направление касательной к кри­вой в данной точке, но длина управляющих линий разная (рис. 4.12). Это говорит о том, что кривизна криволинейных участков, прилегающих к этой опорной точке, различна с разных ее сторон. Математически это значит, что в данной точке нет разрыва первой производной, но вторая производная кривой претерпевает разрыв.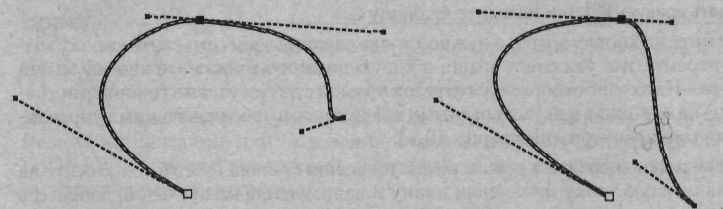


Рис. 4.12. У гладкой узловой точки касательные линии лежат на одной прямой. но имеют разную длину

Изменение длины касательной линии с одной стороны точки привязки путем пе­ремещения управляющей точки приводит к соответствующему изменению радиу­са кривизны этого криволинейного сегмента с одной стороны узловой точки. При этом длина второго отрезка касательной линии (с другой стороны узловой точки) не изменяется.

Острый узел

У острого узла касательные линии с разных сторон этой точки не лежат на одной прямой. Поэтому два криволинейных сегмента, прилегающих к опорной точке, имеют различную кривизну с разных сторон узловой точки и контур в этой точке образует резкий излом (рис. 4.13). Здесь радиус кривизны и угол наклона каса­тельной для каждого криволинейного сегмента можно регулировать независимо друг от друга соответствующим изменением длины и угла наклона касательной линии для каждого прилегающего к опорной точке криволинейного сегмента в отдельности. В частности, один из отрезков касательных может быть равен нулю (рис. 4.14). В этом случае форма сегмента кривой будет регулироваться только одним отрезком касательной, а не двумя, как это было в предыдущих случаях.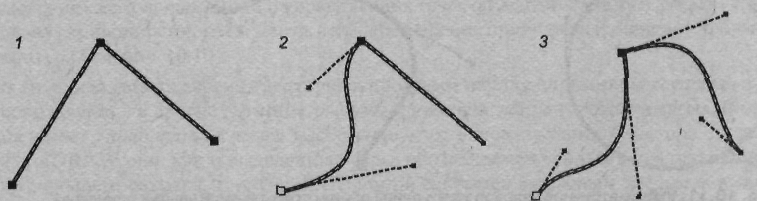



Рис. 4.13. Три варианта острых узлов: без управляющих точек (1), с одной управляющей точкой (2} и двумя (3). В последнем случае кривизну сегментов контура в острой узловой точке можно изменять независимо для каждого сегмента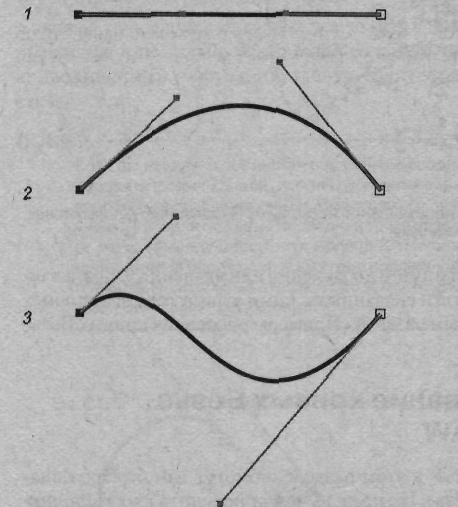



Рис. 4.14. Иллюстрация рисования (1) и редактирования (2, 3) кривой Безье в программе Corel KARA 2 с помощью инструмента Shape Editor (Редактирования фигур)

Примитивы (Формы)

Наряду с разнообразными кривыми, основу которых составляют кривые Безье, векторные редакторы имеют в своем составе специальные инструментальные сред­ства для создания простых форм (графических примитивов), что упрощает постро­ение сложных объектов. В качестве примера такого примитива можно указать на эллипсовидные формы, используемые при рисовании почек на ветке сакуры (рис. 4.5).

Часто наряду со своим прямым назначением простые формы используются в ка­честве исходных заготовок для создания на их базе более сложных объектов. В этом случае для последующего редактирования созданных заготовок необходимо привлечение рассмотренной нами ранее технологии редактирования кривых Безье с помощью пе­ремещения узлов и управляющих точек. Однако все не так однозначно. Для осу­ществления этой процедуры в некоторых редакторах требуется выполнить специ­альное преобразование примитивов в кривые Безье, поскольку их математическое описание в некоторых редакторах отличается от формул, заложенных в построе­ние кривых Безье.


Рис. 4.15. Палитра Swatches (Каталог) предназначена для выбора цвета обводки в Adobe Illustrator 9

Комбинированные объекты

Как вы могли уже убедиться при знакомстве с разделом «Структура векторного рисунка», векторное изображение может состоять из десятков и сотен объектов (контуров). Все они сначала создаются как простые объекты, из которых затем формируется сложный объект. Достигнутый в результате этих действий резуль­тат необходимо зафиксировать, чтобы избежать при выполнении последующих операций искажения рисунка из-за возможного изменения соотношения пропор­ций между объектами или их взаимного расположения. Для этих целей в вектор­ных редакторах предусмотрена группа базовых операций, включающих:

• 
  группировку объектов;
  
• 
  объединение объектов;
  
• 
  использование составных контуров.
  

Группировка объектов

Операция группировки состоит в объединении двух или более объектов (конту­ров) водну группу. С полученным таким образом сгруппированным объектом можно обращаться как с единым объектом. Его можно перемешать, поворачивать, растягивать и выполнять многие другие операции без искажения взаимного рас­положения и пропорций входящих в него объектов.

При реализации операции группировки можно использовать несколько уровней группировки. В этом случае разгруппировка объектов происходит в обратном по­рядке с сохранением иерархии группировки.

Объединение объектов

Объединенный объект (контур) создается путем использования одной или несколь­ких операций по объединению двух или нескольких контуров. В результате такой операции из нескольких объектов получается новый объект, обладающий свой­ствами самого верхнего из исходных объектов, участвующих в операции. Поэтому в отличие от рассмотренной ранее операции группировки здесь свойства состав­ляющих объектов теряются.

В современных векторных редакторах предусмотрены различные варианты слия­ния объектов. Наиболее распространенными из них являются три процедуры, прин­цип действия которых основан на использовании базовых логических операций ИЛИ, И, И-НЕ.