Конспект лекций по дисциплине силовая электроника по направлению 140400. 62

• Название: Конспект лекций по дисциплине силовая электроника по направлению 140400. 62
• Дата: 06.06.2022
• Размер: 1.41 Mb.
• Имя файла: Konspekt_po_SE_Ch1.doc
• Тип: Конспект лекций; #572801
• страница: 3 из 12

В.2 Методы анализа работы преобразовательных устройств

В.2.1 Метод припасовывания (сшивания)

Если реальную вольтамперную характеристику нелинейного элемента можно заменить ломаной линией с конечным числом линейных участков, то в пределах линейного участка нелинейный элемент можно заменить эквивалентным линейным элементом и получить линейную схему замещения всей электрической цепи. Для линейной схемы замещения можно составить систему линейных дифференциальных уравнений, связывающую токи и напряжения этой схемы замещения. Метод впервые применил академик Н.Д. Папалекси в 1912 году, но до настоящего времени это достаточно точный и широко применяемый метод.
Метод припасовывания включает следующие этапы:

1. 
   Замену реальных вольтамперных характеристик ломаными прямыми и получение набора линейных схем замещения.
   
2. 
   Составление и решение систем линейных дифференциальных уравнений для всех линейных схем замещения. Решения линейных дифференциальных уравнений будут включать неизвестные начальные условия, подлежащие определению.
   
3. 
   Используя условия перехода нелинейного элемента от работы на одном линейном участке к работе на другом линейном участке и законы коммутации в электрических цепях, припасовывают (сшивают) решения дифференциальных уравнений для соседних участков.
   

Для установившегося периодического переходного процесса дополнительно сшивают решения дифференциальных уравнений для начала и конца периода повторения. В результате сшивания участков получается система уравнений для неизвестных начальных условий. Для установившегося периодического переходного процесса решение этой системы может быть получено в замкнутом виде. При неустановившихся процессах могут быть получены рекуррентные выражения для начальных условий.

Если процесс установившийся периодический, то достаточно рассмотреть период повторяемости процесса, который в многофазных схемах может быть в несколько раз короче периода переменного источника питания.

Проиллюстрируем метод на примере расчета мгновенных значений токов и напряжений в однофазном однополупериодном выпрямителе с емкостным фильтром, схема которого приведена на рис.В.3.




Рис. В.3. Принципиальная схема однофазного однополупериодного выпрямителя с емкостным фильтром
Диод VD1 выпрямляет переменную однофазную ЭДС e_S = E_msin(t), емкость конденсатора С_Ф сглаживает постоянное напряжение U_d. Нагрузка выпрямителя представлена эквивалентным активным сопротивление R_d.

Для упрощения задачи считаем диод идеальным, то есть при прямом напряжении на диоде (плюс на катоде, минус на аноде диода), он обладает нулевым сопротивлением и на нем падает нулевое напряжение, при обратном напряжении сопротивление диода равно бесконечности, а ток диода равен нулю. Вольтамперная характеристика идеального диода состоит, соответственно, из двух линейных участков. На основании законов Кирхгоффа для схемы рис. В.3 можно записать следующую систему уравнений

(В.1)

После подачи переменной ЭДС возникает переходный процесс, который теоретически длится бесконечно долго. По методу припасовывания в этом случае, следует рассматривать бесконечное количество интервалов с открытым и закрытым состояниями диода. Так как в момент подачи ЭДС состояние схемы известно, то задача решается путем последовательного получения решения на каждом интервале.

Решим задачу для установившегося периодического процесса, когда изменения токов и напряжений периодически повторяется с периодом питающей ЭДС. Используя соотношение t, заменим время t на электрический угол . Период повторяемости разобьем на два интервала с открытым и закрытым состоянием диода. На рис. В.4 показаны диаграммы ЭДС, напряжения на нагрузке u_d и тока конденсатора i_C при некоторых параметрах схемы.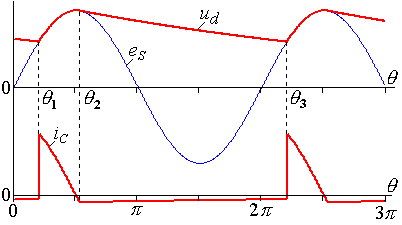



Рис. В.4. Временные диаграммы токов и напряжений в однофазном выпрямителе

Первый интервал: , диод открыт, напряжение на диоде u_V = 0, а система уравнений (В.1) преобразуется к виду

, (В.2)

, (В.3)

где - сопротивление фильтра на основной частоте.

Второй интервал: , диод закрыт, ток диодаi_S = 0 и третье уравнение системы (В.1) преобразуется в уравнение

. (В.4)

Решение уравнения (В.4) имеет вид

, (В.5)

где А – постоянная интегрирования, подлежащая определению.

При известном напряжении u_d, легко определяются остальные токи и напряжения

, (В.6)

, (В.7)

. (В.8)

Уравнения, описывающие изменения токов и напряжений на первом и втором интервале получены, осталось найти постоянную интегрирования А и углы , . Учтя, что при угле ток диода i_S равен нулю, из уравнения (В.3) можно найти угол .

, отсюда

. (В.9)

Используя законы коммутации, а именно, непрерывность напряжения на конденсаторе в момент перехода от первого ко второму интервалу при , в уравнение (В.2) подставим значение напряжения u_d из уравнения (В.5)

и найдем постоянную интегрирования

, где уже определено. (В.10)

Из условия периодичности установившегося процесса и непрерывности напряжения на конденсаторе следует, что напряжение на конденсаторе при угле равно напряжению при угле

, или

. (В.11)

Уравнение (В.11) трансцендентное, и найти из него угол можно только численными методами.

Основное достоинство метода припасовывания – точное описание переходных процессов в преобразователях.

Недостатки метода:

Необходимо составлять и решать несколько систем линейных дифференциальных уравнений, возможно достаточно высокого порядка.

Необходимо состыковывать начальные и конечные условия временных участков, что в ряде случаев возможно только численными методами.

Метод применяется при численном моделировании преобразователей и качественном описании временных процессов.

В.2.2 Метод гармонического анализа

При определенных допущениях можно принять известным вид некоторых токов или напряжений в преобразователе. Тогда известный ток (напряжение) можно заменить эквивалентным несинусоидальным источником тока (напряжения) и анализировать оставшуюся электрическую цепь известными методами ТОЭ для линейных цепей. Особенно удобен этот метод при точно известных моментах включения и выключения ключевых элементов преобразователей.

На рис. В.5, а приведена схема простейшего импульсного преобразователя напряжения (ИПН), использующего для регулирования постоянной составляющей напряжения на нагрузке широтно-импульсную модуляцию (ШИМ) питающего напряжения E_S.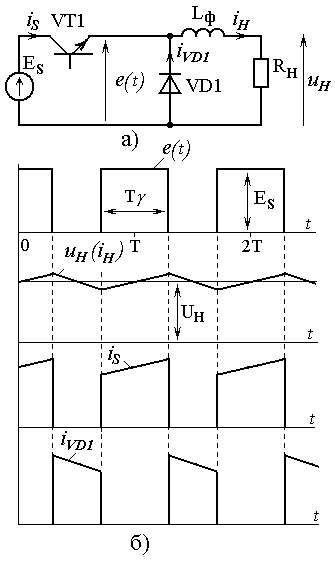




Рис. В.5. Принципиальная схема и временные диаграммы ИПН
Источник постоянного напряжения E_S и транзисторный ключ (тот самый нелинейный элемент, который создает основную проблему при анализе схемы) заменяются эквивалентным источником периодического несинусоидального напряжения e(t).

Если далее получать точные аналитические выражения для токов и напряжений, то мы перейдем к методу припасовывания, но при известных моментах переключения.

Если напряжение эквивалентного источника разложить в ряд Фурье и найти закономерность изменения гармоник при прохождении через фильтр, то мы придем к методу гармонического анализа, который очень широко используется в радиотехнике.

При использовании метода гармонического анализа решение получается в виде суммы гармонических составляющих. Для линейных цепей всегда можно найти аналитическое выражение для коэффициентов передачи гармонических составляющих токов и напряжений от источника этих гармоник к интересующей нас ветви линейной части схемы. Обычно линейная часть схемы обладает хорошими фильтрующими свойствами, то есть с ростом номера гармоники коэффициенты передачи уменьшаются, а высшие гармоники быстро затухают.

Если ограничится анализом прохождения только одной низшей гармоники, то метод гармонического анализа вырождается в метод основной гармоники. Метод основной гармоники является приближенным, применяется, если линейная часть схемы обладает хорошими фильтрующими свойствами, но менее трудоемок, чем метод гармонического анализа.

Пример использования метода гармонического анализа
Для схемы рис. В.5, а разложим напряжение несинусоидального источника e(t) в ряд Фурье. Для напряжения источника e(t), приведенного на рис. В.5, б разложение в ряд Фурье будет содержать постоянную составляющую и только косинусоидальные составляющие высших гармоник.

Коэффициент Фурье для постоянной составляющей равен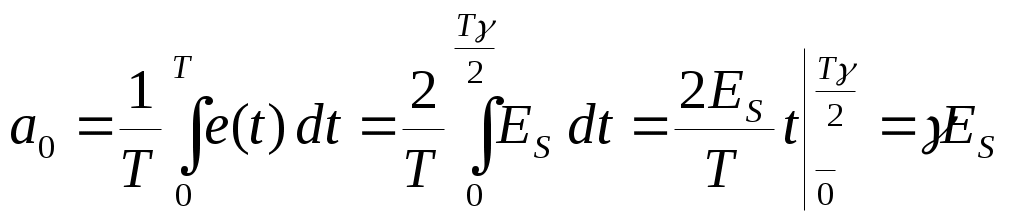

. (В.12)

Коэффициенты Фурье для косинусоидальных составляющих определяются выражением

, (В.13)

где - электрический угол, - частота, k – номер гармоники.

Разложение напряжения e(t) в ряд Фурье с учетом уравнений (В.12) и (В.13) имеет следующий вид

. (В.14)

Комплексный коэффициент передачи напряжения источника e(t) в напряжение сопротивления нагрузки u_H(t) равен

, (В.15)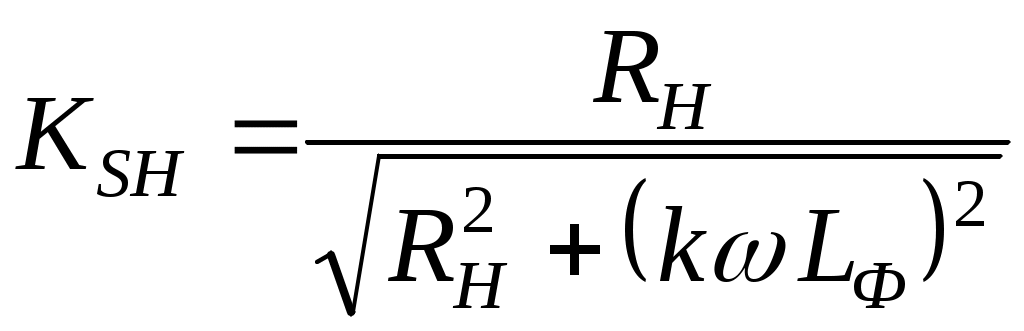

где - модуль коэффициента передачи для k-той гармоники,

- фазовый сдвиг k-той гармоники напряжение на нагрузке.

Напряжение на нагрузке через гармонические составляющие определяется уравнением

. (В.16)

Если выполняется условие , то зависимость модуля коэффициента передачи от номера гармоники описывается приближенной зависимостью

,

где - добротность фильтра для первой гармоники.

Напряжение на нагрузке будет определяться приближенным уравнением

. (В.17)

Из формулы (В.17) видно, что амплитуды гармоник уменьшаются пропорционально квадрату их номера, то есть высшие гармоники быстро затухают, что, при восстановлении формы напряжения на нагрузке, позволяет ограничиться суммированием конечного числа гармоник.

На рис. В.6 приведены восстановленные из суммы гармоник формы напряжения эквивалентного источника и напряжения на нагрузке при учете пяти гармоник, E_S=1, и Q_Ф =4.

В напряжении эквивалентного источника хорошо просматриваются гармонические составляющие, а форма напряжения на нагрузке близка к теоретической, состоящей из участков экспонент.


Рис.В.6 Восстановление напряжения эквивалентного источника и напряжения на нагрузке по пяти гармоникам
Вопросы для самоконтроля

1. Когда применим метод гармонического анализа?

2. Какие свойства линейной части цепи позволяют уменьшить число учитываемых гармоник?

3. Какое напряжение e() или u() более точно реализуется конечным числом гармоник и почему?

4. При какой добротности Q напряжение на нагрузке, полученное по приближенному выражению (В.17), практически не отличается от напряжения, полученного по выражению (В.16)?

5. Используя выражения (В.12)-(В.17) постройте средсвами Mathcad модель ИПН, сравните результаты моделирования с рис. В.6.