ргр. Конспект лекций ПЕРЕСДАТЬ. Конспект лекций по дисциплине "Управление и перспективы развития инфокоммуникационных систем" для докторантов специальности

• Название: Конспект лекций по дисциплине "Управление и перспективы развития инфокоммуникационных систем" для докторантов специальности
• Дата: 15.07.2021
• Размер: 1.63 Mb.
• Имя файла: Конспект лекций ПЕРЕСДАТЬ.docx
• Тип: Конспект лекций; #224364
• страница: 7 из 16

Модели принятия решения в условиях конфликта

Основные этапы процесса принятия решения согласно теории принятия решения декомпозируются на следующие этапы:

• 
  Определение цели решения возникшей проблемы.
  
• 
  Выбор наиболее предпочтительного варианта действий, ведущего к достижению цели.
  
• 
  Реализация решения (выбранного варианта действия).
  

Определение цели решения возникшей проблемы реализуется в блоке интеллектуального преобразователя, получающего и обрабатывающего информацию о внешней среде с системы датчиков. В условиях конфликта цель может зависеть от имеющихся ресурсов и факторов, которые образуют проблемную ситуацию, т.е. ситуацию принятия решения в условиях конфликта. Способ действия для управлении объектом в процессе принятия решения называют стратегиями, а результат к которому может привести выбранная стратегия называют исходом. Условия конфликта порождают факторы, воздействующие на стратегию и соответственно на управление, реализуемое интеллектуальной системой. С точки зрения наличия информации об условиях конфликта факторы разделяются на две группы:

• 
  определенные (фиксированные) факторы, значения которых известны;
  
• 
  неопределенные факторы, о которых априорно не известно, какое значение они примут.
  

В зависимости от происхождения неопределенные факторы делятся на случайные и неопределенные нестохастического характера, состоящие из природных и стратегических. Математическая модель принятия решений формируется с учетом всех факторов и имеющейся о них информации. Упрощенная модель принятия решения в этом случае может быть описана следующей системой
D₀ = < Y, G, U, L, J, Ω>, (1)
Где Y- множество исходов (результатов);

G- модель предпочтений исходов (принимаемых решений);

U- множество стратегий принятия решений,

L- множество возможных значений неопределенных факторов;

J- функция, определяющая взаимосвязь неопределенного фактора и исход, получаемый в результате принятого решения;

Ω- вся остальная информация о принимаемом решении в формализованном виде( сведения о конфликте, предпочтения других лиц , участвующих в конфликте и др.).

Удобство использования модели (1) в условиях конфликта определяется тем положением, что она позволяет просто и наглядно связать значения неопределенных факторов и стратегий с управлением, реализуемым интеллектуальной системой. Множества Y, G, U, Lи функция J формально задают компоненты принимаемого решения и определяют связь с системой управления через понятия критерия и показателей эффективности системы. В теории управления наиболее часто отношения предпочтения описываются с помощью специальных функций : показателей качества и критериев. Под показателем W качества или эффективности системы управления понимается мера степени соответствия реального результата управленияY требуемому Y^тр для достижения цели и получения оценок или измерений интенсивности исходов. Под критерием К понимается правило, позволяющее сопоставлять принимаемые решения и стратегии с точки зрения выбранных показателей оценок исходов. Критерии вводятся на основе определенной концепции рационального поведения интеллектуальной системы пригодности, оптимизации и адаптивизации.

Более общей моделью принятия решения в условиях конфликта по сравнению с (1) является модель динамической системы интеллектуального управления на основе моделей теории игр и современного аппарата функционального анализа

Теория игр как раздел математики в настоящее время стал теорией математических моделей [29] . При этом под конфликтом понимается явление, которое связано с ответом на вопросы:

• 
  Кто и как в этом явлении участвует?
  
• 
  Каковы возможные исходы конфликта?
  
• 
  Кто в этих конфликтах заинтересован?
  
• 
  В чем состоит заинтересованность участников конфликта?
  

Для описания конфликта вводится понятия:

• 
  коалиций действия RД, объединяющее множество игроков (участников конфликта) по их действиям;
  
• 
  коалиций интересов RД объединяющих игроков по интересам;
  
• 
  стратегий, характеризующих решения коалиций К (действий RД и коалиций интересов RИ, которые в зависимости от типа игры могут иметь одних и тех же игроков или образовываться из разных игроков);
  
• 
  отношений предпочтения G, как абстрактного бинарного отношения на множестве всех стратегий (нередко отношения предпочтения задаются функцией выигрыша W_K и тогда коалиция К, если она предпочитает ситуацию x ситуации y, то обозначают через отношение предпочтение в виде x G_K y или при использовании функции выигрыша, если W_K (x)W_K (y), то в виде x W_K y).
  

Тогда формальное описание конфликта состоит в задании системы
Г = < R_Д , S_RД, S, R_И, G_RИ >, (2)
где S_RД- множество стратегий коалиции действия;

G_RИ – множество отношений коалиции интересов,

при этом множества и отношения, которые связаны между собой в соответствие со сделанными выше их описанием в зависимости от конкретного содержания конфликта.

В работе [30], как и в ряде других исследованиях по общей системной теории управления, предложено рассматривать динамические системы управления состоящие из объекта управления, характеризуемого некоторым множеством состояний, и регулятора, под которым понимается математическая модель, состоящую из элемента, обеспечивающего оценку состояния объекта, и элемента, формирующего управление.

Для описания динамической системы используется математическая модель совокупности элементов, удовлетворяющих следующим основным аксиомам:

А) Заданы множества моментов времени Т, множество состояний системы Х. Множество значений входных воздействий U, непустое множество их допустимых значений
 = {: TU}, (3)
множество значений выходных величин Y и множество их допустимых значений
 = {: TXY}. (4)
В) Множество Т есть некоторое упорядоченное подмножество множества вещественных чисел (направление времени).

С) Существует переходная функция
Ф={: ТТХХ}, (5)
где состояния системы х(t) =[t, t₀, x(t₀), ]X.

D) Задано входное отображение
 = {: TXY}. (6)
Приведенная модель в наиболее общем виде динамического объекта или системы изображена на рис..5.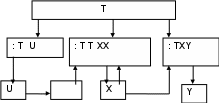



Рисунок 1 - Множественная схема динамической системы

Для описания динамической системы используются дополнительные термины. Так, состояние системы х в момент времени t, или пара элементов множества TX называется событием (или фазой) динамической системы. Множество TX называется пространством событий, или фазовым пространством. В том случае, когда множество выходных воздействий используется для управления, то оно называется управлением. Управление переводит систему из одного состояние в некоторое другое. При этом система находится в движении, описывая в пространстве состояния траекторию. В рассмотренной формализации динамическая система рассматривается как объект управления.

Для реализации систему управления в классической теории систем выделяют объект управления и регулятор управления, состоящий в простейшем случае из элемента оценки состояния системы и элемента, формирующего закон управления. Так как объект управления нами уже рассмотрен как динамическая система, то введем понятия закона управления и оценки состояния системы.

Законом управления принято называть отображение
k : TX  U, (7)
где величины u(t) = k[t; x(t)] управления, принадлежащие множеству U.

Для реализации управления необходимо знание переменных состояния системы х(t), что требует операции определения обратного отображения
^-1 : Y  X (8)
и тогда координаты системы определяются из условия
x(t) = ^-1[y(t)]. (9)
Кроме того для оценки состояния системы необходимо оценивать точность определения x(t), т.е. получать оценку состояния x₀(t).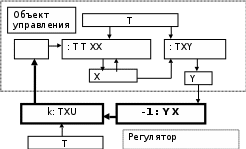





Рисунок 2 - Структурно- логическая схема блока основного управления системы
Структурно – логическая схема системы управления, состоящая из объекта управления и регулятора, показана на рис. 10.6. Для учета факторов воздействия внешней среды и конфликта необходимо провести учет воздействий этих объектов. При этом факторы внешней среды и условий конфликта необходимо рассматривать и описывать с позиций динамической системы.

При принятии решения в системе интеллектуального управления возникает необходимость объединения интеллектуального преобразователя, включающего блок принятия решения, и динамическую систему управления.

Определение оптимальной интеллектуальной системы принятия решения и управления в условиях конфликта

Понятие оптимальности получило широкое распространение в теории управления и теории принятия решений [13, 22-25]. Под оптимальной системой автоматического управления понимают «наилучшую» систему, которую выбирают из множества систем по принятому показателю качества системы или эффективности ее функционирования. При этом система является оптимальной, если она обеспечивает экстремум принятого показателя. В зависимости от конкретного вида показателя понятие оптимальности связывается с критерием, т.е. с минимумом или максимумом показателя. Если, например, в качестве показателя используется средняя квадратическая ошибка системы, то оптимальной системой считают ту, которая реализует критерий – минимумом средней квадратической ошибки. Если же в качестве показателя используется вероятность невыхода ошибки системы из заданных допусков, то оптимальной считают ту систему, которая реализует критерий – максимум невыхода ошибки системы из заданных допусков.

Принятие решений в условиях определенности (фиксированности) факторов и в случае, когда неопределенность является случайной и о факторе имеется полная априорная информация, то оптимальность решения определяется аналогично тому, как это делается в системах автоматического управления.

В условиях стратегической (поведенческой) неопределенности, которая появляется в условиях конфликта, понятие оптимальности принимаемого решения значительно труднее поддается формализации. Теория математических моделей принятия оптимальных решений составляет значительную часть науки, которая получила название исследования операций [1]. Особое место в исследовании операций занимает раздел, занимающейся теорией математических моделей принятия оптимальных решений в условиях конфликта, который получил название теории игр [29]. Теории игр, как теория математических моделей базируется на использовании формальных, знаковых моделей для описания конфликта, а также использует формальные средства их анализа. В теории игр успешно были реализованы определения понятия конфликта и принятия решения. В тоже время понятие оптимальности удалось в настоящее время реализовать только для части игр. Поэтому при анализе систем принятия решений и управления мы ограничимся рассмотрением только тех конфликтов, которые описываются моделями бескоалиционных (множества коалиций действия и интересов совпадают, определены функции выигрыша) и антагонистических (число игроков равно двум, а значения их функций выигрыша в любой ситуации равны и противоположны по знаку) игр. Для бескоалиционных и антагонистических игр условия оптимальности основываются на понятии равновесия.

Вопрос об оптимальности управления и принятия решений в интеллектуальных системах усложняется и тем фактом, что для реализации системы используются экспертные знания, которые не всегда удается реализовать. Эта трудность преодолевается за счет допущения, что в системе реализуется интеллектуальный датчик, который однозначно определяет информацию о действиях другой стороны за счет физических измерений действия противоположных игроков, воздействующих на систему управления и принятия решения в условиях конфликта. Фактически в интеллектуальной системе реализуется рациональное управление и принятие решения. Достоверность и степень приближения к точному оптимальному управлению и принятию решения определяется той информацией, которую получает, отрабатывает и выдает интеллектуальная система, или интеллектуальный датчик. При этом в результате ошибок интеллектуального датчика, связанных с использованием экспертных знаний, появляются риски, связанные с ошибочным формированием цели принятия решения и управления, определением показателей и критериев оценки эффективности работы системы, выбором лучшей системы. Для уменьшения рисков в интеллектуальной системы используются методы обучения и самообучения, которые в настоящее время начинают разрабатываться в интеллектуальных системах и которые всегда присутствовали в биологическом интеллекте [17-21].

Решение задач синтеза систем оптимального управления и принятия решения в условиях конфликта традиционно связаны с математическими методами отыскания экстремумов функций и функционалов, нахождения равновесных состояний, что позволяет решать задачи синтеза систем управления и принятия решений в практически важных случаях.

Рассмотрение структуры систем интеллектуального принятия решения и управления в условиях конфликта (рис. 3) показывает, что система состоит из трех основных элементов (подсистем), каждый из которых имеет свои модели и специфические методы исследования:

- интеллектуальная подсистема;

-подсистема принятия решения;

- подсистема управления объектом и объект управления.

Внешняя среда: окружающая среда и конфликтующие системы






Интеллектуальная подсистема, включающая датчики, базу знаний, блоки экспертизы, оценки состояния и др.

Подсистема управления объектом и объект управления







Подсистема принятия решения

Рисунок 3 - Структура интеллектуальной системы принятия решения и управления в условиях конфликта, порождаемого конфликтующими системами
Не смотря на свою сложность и методологические особенности элементов интеллектуальных систем принятия решения и управления в условиях конфликта при определении оптимальной системы, удается выделить следующие основные задачи:

• 
  построение модели условий конфликтного взаимодействия оптимизируемой системы с другими системами, изучение и описание информации о воздействиях на систему;
  
• 
  формирование интеллектуальной подсистемы, включающей датчики, базу знаний, блоки экспертизы, оценки состояния, формирования целей, выбор показателей и критериев оптимизации системы и других элементов интеллектуальной деятельности;
  
• 
  принятие решений, обеспечивающих оптимальное противодействие одной или нескольким конфликтующим системам;
  
• 
  определение и математическое описание классов допустимых систем управления объектом управления;
  
• 
  отыскание экстремума критерия или точек равновесия в игровых задачах, а также соответствующих им характеристик.
  

Формирование модели условий конфликтного взаимодействия оптимизируемой системы с другими системами основывается в простейшем случае с позиции теории игр как конфликт двух игроков (А, В). При этом конфликт рассматривается как операция, в которой игроки имеют различные цели и реализуют свою деятельность и выбирают свои стратегии в соответствии со своими целями рис.4[1, 24-26]. Исследование операции проводится всегда с точки зрения одного игрока, а в рассматриваемом случае это проводится с позиции интеллектуальной системы принятия решения и управления (для определенности примем, что в конфликте – это игрок А). Будем считать, что эффект достижения цели определяется векторными показателем W = (W_А, W_В) и критерием К = (К_А, К_В), связанные с целями поведения сторон. При этом в зависимости от наличия датчиков получения информации о целях действия игроков предполагается, что идентификация целей позволяет интеллектуальной системе определять критерии и показатели, используемые игроками для идентификации показателей и критериев игроков.


Игрок В

Внешняя среда





Критерий

К

Показатель W


Конфликт




W


Интеллектуальная подсистема

Объект управления






Подсистема принятия решения

Подсистема управления объектом




Игрок А: интеллектуальная система

принятия решения и управления


Рисунок 4 - Общая схема конфликта как операции двух систем с разными целями
Вопросы формирование интеллектуальной подсистемы, включающей датчики, базу знаний, блоки экспертизы, оценки состояния, формирования целей, выбор показателей и критериев оптимизации системы и других элементов интеллектуальной деятельности были рассмотрены в первом разделе лекции, когда анализировались интеллектуальные системы и их элементы.

Принятие решений, обеспечивающих оптимальное противодействие одной или нескольким конфликтующим системам конфликтующим системам, основывается в условиях конфликта на использовании моделей, методов и алгоритмов принятия оптимальных решений в теории игр. В рассматриваемом нами случае мы ограничиваемся матричными антагонистическими (игры двух лиц с нулевой суммой), которые имеют развитый инструментарий решения прикладных задач

Определение и математическое описание классов допустимых систем управления объектом управления основывается на теории систем управления [1]. В основе рассматриваемой задачи оптимизации системы управления объектом используется подход, основанный на использовании корреляционной теории статистической оптимизации систем, разработанной профессором Н. И. Андреевым. В его работах разработаны методы исследования сложных линейных и нелинейных динамических систем, подверженных случайным воздействиям. При постановке задач определения оптимальных динамических систем по статистическим критериям (по минимуму средней квадратической ошибки системы, максимуму вероятности невыхода ошибки системы из заданных допусков и др.) им разработана методология учета ограничений типа неравенств, накладываемые на функции управления и вектора. Большое внимание им уделено исследованию динамических систем с заданной структурой, так как для прикладных задач эти системы играют, с одной стороны, важную роль, а, с другой стороны, приводят к значительному усложнению математических задач оптимизации этого класса систем. В его работах исследовано ряд новых задач, относящихся к оценке параметров системы, фильтру Калмана, синтезу нелинейных динамических систем, построению адаптивных систем оценивания и управления, развитию методов принятия статистических решений, определению оптимальных систем управления с решающими устройствами.

Модели систем управления, которые являются подсистемой интеллектуальной системы принятия решений и управления в условиях конфликта, на базе теоретико-множественного подхода описаны в лекции 10.3, где они заданы основными соотношениями (10.7-10.13).

Отыскание экстремума критерия или точек равновесия в игровых задачах, а также соответствующих им характеристик, для построения интеллектуальной системы принятия решений и управления в условиях конфликта основывается на современной теории игр в тех случаях, когда удается формализовать все элементы и факторы конфликта. Для формализации задач интеллектуальной обработки информации могут быть использованы методы информационной математики, которые были проанализированы в разделе 10.1.4.

Проиллюстрируем проведенный анализ постановки задачи определения оптимальной интеллектуальной системы принятия решения и управления в условиях конфликта на простом примере, который был рассмотрен в работе [33] в иной постановке задачи оптимизации.

Пример. Рассмотрим задачу определения интеллектуальной системы принятия решения и управления, на вход которой поступает сигнал, представляющего сумму полезного сигнала G(t) и помехи Z(t). При этом будем предполагать, что слежение за полезным сигналом осуществляет интеллектуальная система управления (игрок А), а помеху формирует противоположная сторона (игрок В), которая выбирает характеристики такими, чтобы ошибки следящей системы были большими. В результате возникает конфликт, который часто рассматривается в теории игр. Для наглядности и простоты изложения будем полагать, что каждая из сторон имеет две стратегии управления и по этой причине можно ограничить решение задачи на основе матричной и биматричной игр.

Пусть помеха представляет собой нормально распределенный белый шум с интенсивностями (α1, α2), выбором величины которых управляет игрок А. Полезный сигнал G = G₀ числовая случайная величина, принимающая значения β₀ и -β₀ с вероятностью 0,5, величина которых формируется игроком А и может принимать значения (β₀₁, β₀₂).

Желаемая выходная величина формируемой системы слежения - полезный сигнал. Система выбирается на классе стационарных систем, время регулирования которых не превосходит время Т.

В качестве показателя качества системы принимается суммарная ошибка системы ошибка системы D_∑, которая определяется биноминального распределения полезного сигнала D₁ и случайным характером помехи D₂. Следуя работе [32], запишем ошибки системы в следующем виде:
Т Т

D₁ = ∫ ∫ δ(τ₁- τ₂)ω(τ₁ ) ω(τ₂ )d τ₁d τ₂,

0 0
Где δ(τ₁- τ₂) – дельта-функция, принимающая нулевое значение, если ( τ₁- τ₂)≠0, и равна ∞, если( τ₁- τ₂)=0 ;

ω(τ₁ ) – весовая функция при переменной τ₁;

ω(τ₂ ) – весовая функция при переменной τ₂ ;

Т

D₂ = (β₀ )² { ∫ ω(τ) d τ₁ - 1}²;

0

D_∑ = D₁ + D₂.
Базовая подсистема управления будет описываться весовой функцией, параметры которой зависят от решения игровой задачи и выбора подсистемой интеллектуального управления цели системы и соответствующих показателей и критериев оптимизации.

Тогда для иллюстрационного примем Т =1 и выражение для весовой функции можно записать в виде
ω_IJ(τ ) = β²_0J (α_i + β²_0J )^-1 ,
где управление реализуется в виде весовых функций в зависимости от стратегий игроков (В - максимизирует дисперсию ошибки, а А -минимизирует ошибку слежения).

В этом случае дисперсии для принятой весовой функции записываются в следующем виде, учитывающем стратегии игроков
D₁^IJ= α_i (α_i β^-2_0J +1)^-2,

D₂^IJ = α_i ² β²_0J (α_i + β²_0J )^-2.
Интеллектуальная подсистема В, наблюдая с помощью своих информационных и физических датчиков за игроком А, определяет его действия и формирует свою стратегию движения в каждой конкретной ситуации. Возникает задача ситуационного управления движением, когда решения и управления должны осуществляться в соответствие с той ситуацией, которая складывается в текущий момент конфликта.

Одной из сложных задач в этом случае является задача определения типа антагонизма между игроками и определения целей действия систем, выяснения их интересов. В практике конфликтных ситуаций о действиях другой стороны или игрока, как правило, используется информация, получаемая через информационные сообщения, телекоммуникационные сети и путем сбора различными способами конфиденциальной информации. При реализации интеллектуальной экспертной системы используются эксперты и их оценки, но и возможен аналитический подход к решению идентификации намерений и цели противоположной стороны на основе анализа конфликта. Если реализуется интеллектуальная подсистема на основе ситуационного управления, то возможна декомпозиция общей задачи на две части, когда интеллектуальная подсистема идентифицирует конкретную ситуацию, а управление в конкретной ситуации формируется на основе решения игровых задач для определения неопределенных стратегий, или неопределенных параметров противодействующей стороны. Вместе с тем интеллектуальная подсистема должна определять тип модели игры в конфликте. Возникает вопрос, как это может реализовать интеллектуальная подсистема. Существует ли такая возможность?

Покажем возможность оценки действий противника на основе обработки информации по решению задачи с помощью теории игр. Для этого проанализируем результаты принятия решения при реализации матричной антагонистической игры. Вначале рассмотрим влияние конфликта на управление на примере единичной ситуации, когда время управления Т фиксировано и единственное, а затем рассмотрим условную модель ситуационного управления на основе сценария, в котором достижение цели обеспечивается несколькими ситуациями управлениями в разные моменты времени Т_ν.

Примем, что игроки могут реализовать по две стратегии, т.е. конфликт описывается матрицей размерности 2х2, где (β²₀₁ = 1, β²₀₂= 2) значение стратегий игрока В и (α₁ = 1, α₂ = 2) значение стратегий игрока А. В этом случае при принятых исходных данных матрицы выигрышей можно записать в следующем виде:

• 
  при анализе системы по дисперсии D₂
  

  Стратегии В \ А β201 = 1 β202= 2 Min по j Max min = α1 = 1 0,5 0, 667 О,5 0,5 α2= 2 0, 333 0,4 0,4 Max по i 0,5 0,667
  Minmax =	0,5

• 
  при анализе системы по дисперсии D₁
  

  Стратегии В \ А		β201 = 1	β202= 2	Min по j	Max min =
  α1 = 1		0, 25	0,011	0,011
  α2 = 2		0,011	0,08	0,08	О,08
  Max по i		0,011	0,08
  Minmax =	0,08

• 
  при анализе системы по дисперсии D_∑
  

Стратегии В \ А	β201 = 1	β202= 2	Min по j	Max min =
α1 = 1	0,75	0,678	0,678
α2 = 2	0,344	0,48	0,48	0,48
Max по i	0,75	0,48
Minmax =	0,48

Все три антагонистические игры имеют седловые точки

max min D_µ^ij = min max D_µ, µ=(1, 2, 3), i=J=(1, 2)

ijji
в чистых стратегиях, но цены игр у них разные. Интересным результатом анализа дисперсий ошибок анализируемой системы является то, что гарантированная суммарная ошибка системы (равна 0,48) меньше гарантированной ошибки, получаемой только при учете нормальной составляющей ошибки (равной 0,5). Понятно, что полученное уменьшение дисперсии суммарной ошибки в результате отказа от стратегии α₁, которая ведет к увеличению дисперсии нормальной составляющей ошибки. Это также связано с тем, что дисперсии ошибок от изменения сигнала помехи существенно меньше при α₂ влияют на дисперсию D₁. По этой причине , если игрок А будет выбирать свою стратегию из условия увеличения дисперсии помехи, то он может быть наказан игроком В, который в этом случае может реализовать свою стратегию β²₀₁ = 1 (провести адаптивное управление) благодаря этого получить дополнительный выигрыш, который будет равен 0,344, т.е. меньше гарантированного выигрыша на 0,135 (уменьшает дисперсию на 28.5%). Таким образом интеллектуальная подсистема на основе получения оценок интенсивности шума сожжет определить, какой стратегии придерживается игрок А при противодействии игроку В. Логика рассуждений интеллектуальной подсистемы может быть продолжена в том направлении, если игрок В откажется от использования гарантированных оценок, а будет применять критерии: минимаксного сожаления Сэвиджа, пессимизма-оптимизма Гурвица, «недостаточного основания» Бернулли [8].

Рассмотрим теперь случай, когда для достижения цели управления необходимо выполнения нескольких операций по слежению, согласно определенному сценарию (рис.5), в котором последовательно реализуются три ситуации со временем управления Т₁=1, Т₂=2, Т₃ =3 а также показано начало работы системы и достижение цели в случае успешного выполнения все планируемых операций.


Т₁

Т₂

Т₃

Достижение цели

Начальное состояние


Рисунок 5 - Сценарий на основе сетевой модели, вершины которой соответствуют фактом, а дуги связям.
В качестве критерия эффективности достижения цели примем условие получения оптимальных оценок в каждой ситуации, как это было сделано в первой ситуации при Т₁.

Для произвольного Т_ν дисперсии и определяемые весовые функции будут равны

D₁^IJ= Т_ν α_i (α_i β^-2_0J + Т_ν)^-2,

D₂^IJ = α_i ² β²_0J (α_i + Т_ν β²_0J )^-2,

ω_IJ(τ ) = β²_0J (α_i + Т_ν β²_0J )^-1,

где ν = (1, 2, 3), i =(1, 2), J=(1, 2), если использовать данные , принятые в начальных расчетах дисперсий и весовой функции при Т1.

Одним из интересных предложений по развитию интеллектуальной подсистемы для оценки степени антагонизма между игроками и соответственно между интеллектуальными системами в условиях конфликта стало использование теории биматричных игр.

В итоге лекции рассмотрена задача определения интеллектуальной системы принятия решения и управления в условиях конфликта. Определение интеллектуальной системы основывалось на возможности декомпозиции системы на три подсистемы: подсистему интеллектуального управления, подсистему принятия решения и подсистемы базового управления, которая организовывала воздействия на объект управления, функционирующий в условиях конфликта.

Вначале лекции рассмотрено современное состояние исследований интеллектуальных систем, которое базируется на анализе основных направлениях развития искусственного интеллекта и его приложениях в информационных системах, связанных с автоматизацией различных видов деятельности человека. Основное внимание в лекции было уделено анализу экспертных систем, ситуационному управлению и интеллектуальным технологиям мониторинга и управления структурной динамикой сложных технических систем. Очень коротко в лекции затронуты вопросы моделирования и исследования искусственного интеллекта на основе теории функциональных систем П. К. Анохина и современного математического описания интеллектуальных систем с помощью радикалов, ультрасистем, ультраоператоров, предложенных и развиваемых в работах А. В. Чечкина.

В основу построения интеллектуальных систем управления положены исследования, выполненные Н. И. Андреевым, который создал теорию статистически оптимальных систем управления и провел оптимизацию адаптивных систем и системам с решающими устройствами. Им первым было предложена декомпозиция сложных динамических систем на базовый или основной контур управления и подсистему решающего устройства, включая и решения на основе теории игр. По аналогии с работами Н. И. Андреева в лекции предложена декомпозиция интеллектуальных систем принятия решения и управления на три взаимосвязанные подсистемы: интеллектуальную, принятия решения и базового управления. Можно при этом заметить, что объединение интеллектуальных подсистем с системами управления в методическом плане является более сложной и приближенной задачей, так как приходится объединять систему слабо формализуемых экспертных и человеческих знаний и формализованные системы управления. Вместе с тем современное развитие интеллектуальных систем убеждает в том, что надежды слияния искусственного интеллекта и систем управления можно ожидать в ближайшее время, что подтверждается большим объемом публикаций крупных ученых в этой области.

Большое внимание в лекции уделено построению моделей конфликта и осуществлена попытка формализации конфликтной ситуации. В основу подхода к построению моделей конфликта положены абстрактные множественные модели, которые находят применение в теории управления и в интеллектуальных системах. В этом плане делаются только первые шаги, но нет сомнений, что на этом направление вполне реально появится возможность решить задачи объединения части разделов теории игр и искусственного интеллекта с теорией управления. Например, базой такого объединения может стать информационная математика.

В заключение лекции: Это необходимость объединения систем управления с системами адаптивно-игровыми системами , использование которых открывает широкие возможности эффективного управления различной деятельностью человека в условиях конфликта

Литература: 9,10,11, 12, 13, 14, 15, 16
13-14 Лекция. Установка телекоммуникационного оборудования в ОС Linux.

Цель лекции: Освещаются вопросы конфигурирования сервера электронной почты для работы и с рабочими станциями в ЛВС, и с провайдером Internet. В начале лекции дается краткий обзор телекоммуникационных устройств, которые могут работать в ОС Linux. Затем описывается процесс установки и настройки сетевых адаптеров.

Содержание:

• 
  Телекоммуникационные устройства в ОС Linux
  
• 
  Установка и конфигурирование сетевых адаптеров
  
• 
  Установка модемов
  
• 
  Конфигурирование модемов в ОС Linux
  
• 
  Управление модемами в ОС Linux