конспект. КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальносте. Конспект лекций по физике для студентов 12 курсов специальностей технического профиля спо раздел Электростатика Ейск, 2017
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
8.1. Поляризация диэлектриков. Диэлектрики – это вещества, не содержащие свободных заряженных частиц (т. е. таких заряженных частиц, которые способны свободно перемешаться по всему объему тела). Существует два основных вида диэлектриков: неполярные и полярные. П 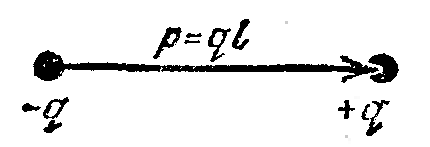 режде, чем мы объясним разницу между ними, дадим одно определение: совокупность равных по величине, но противоположных по знаку двух точечных зарядов -q и +q, сдвинутых друг относительно друга на некоторое расстояние l, называется электрическим диполем. Пусть режде, чем мы объясним разницу между ними, дадим одно определение: совокупность равных по величине, но противоположных по знаку двух точечных зарядов -q и +q, сдвинутых друг относительно друга на некоторое расстояние l, называется электрическим диполем. Пусть 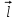 – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор 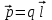 называется электрическим моментом диполя или дипольным моментом. называется электрическим моментом диполя или дипольным моментом.У молекулы неполярного диэлектрика (эбонит, янтарь) при отсутствии внешнего электрического поля центр тяжести отрицательных зарядов внутри молекулы совпадает с центром тяжести положительных зарядов внутри молекулы. Такая молекула не обладает дипольным моментом и называется неполярной. Молекула полярного диэлектрика и при отсутствии внешнего электрического поля обладает дипольным моментом и называется полярной. У полярных диэлектриков (вода, спирт, твердый сероводород H2S) при отсутствии внешнего поля, благодаря тепловому движению, моменты молекул ориентированы по-разному. Если мы выделим объем  диэлектрика, содержащий достаточно большое число молекул, то векторная сумма моментов всех молекул диэлектрика, содержащий достаточно большое число молекул, то векторная сумма моментов всех молекул 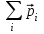 . находящихся в этом объеме, будет равна нулю. При наличии внешнего электрического поля диполи частично повернутся по полю, сумма моментов . находящихся в этом объеме, будет равна нулю. При наличии внешнего электрического поля диполи частично повернутся по полю, сумма моментов 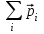 станет отличной от нуля и тем более отличной, чем сильнее поле. Диэлектрик с ориентированными в той или иной степени дипольными моментами окажется поляризованным. станет отличной от нуля и тем более отличной, чем сильнее поле. Диэлектрик с ориентированными в той или иной степени дипольными моментами окажется поляризованным. За меру поляризации диэлектрика примем вектор 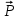 , равный суммарному моменту молекул , равный суммарному моменту молекул 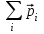 отнесенному к единице объема: отнесенному к единице объема: 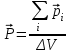 . .Объем 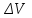 , в пределах которого берется сумма моментов отдельных молекул , в пределах которого берется сумма моментов отдельных молекул 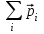 должен содержать достаточное количество молекул, но вместе с тем быть настолько малым, чтобы внутри него все макроскопические величины – плотность, температура, напряженность электростатического поля должен содержать достаточное количество молекул, но вместе с тем быть настолько малым, чтобы внутри него все макроскопические величины – плотность, температура, напряженность электростатического поля  и т. д. – могли считаться постоянными. Вектор и т. д. – могли считаться постоянными. Вектор 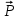 носит название вектора поляризации. носит название вектора поляризации. Степень ориентации молекул естественно положить пропорциональной напряженности поля  в пределах диэлектрика. Тогда и вектор поляризации в пределах диэлектрика. Тогда и вектор поляризации 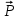 окажется пропорциональным напряженности поля окажется пропорциональным напряженности поля  : : 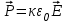 , ,где коэффициент 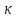 называется диэлектрической восприимчивостью. называется диэлектрической восприимчивостью.У неполярных диэлектриков первоначально молекулы не обладают дипольным моментом (неполярные молекулы), но под влиянием внешнего электрического поля заряды в них смещаются, и у них появляются дипольные моменты 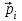 . И в этом случае сумму моментов можно считать пропорциональной напряженности поля, т. к. . И в этом случае сумму моментов можно считать пропорциональной напряженности поля, т. к. 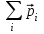 будет возрастать по двум причинам: благодаря увеличению моментов молекул будет возрастать по двум причинам: благодаря увеличению моментов молекул 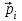 и благодаря их ориентации. Таким образом, последнее соотношение справедливо для молекул любого типа. и благодаря их ориентации. Таким образом, последнее соотношение справедливо для молекул любого типа. Если диэлектрик помещают в электрическом поле, то любой элемент его объема 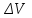 , содержащий достаточно большое число молекул, остается нейтральным. Не так обстоит дело в тонком слое у поверхности диэлектрика. Благодаря повороту молекул у той границы, где входят линии напряженности, получится избыток отрицательных концов молекул, а у той границы, где линии напряженности выходят, – избыток положительных концов молекул. , содержащий достаточно большое число молекул, остается нейтральным. Не так обстоит дело в тонком слое у поверхности диэлектрика. Благодаря повороту молекул у той границы, где входят линии напряженности, получится избыток отрицательных концов молекул, а у той границы, где линии напряженности выходят, – избыток положительных концов молекул.Поверхностные заряды, возникающие при поляризации диэлектрика, носят название связанных. Все прочие заряды (не обусловленные явлением поляризации) носят название свободных. Между вектором поляризации и поверхностной плотностью зарядов, выступающих на границе диэлектрика, существует простая связь: 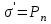 , ,т. е. плотность поверхностных связанных зарядов 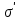 численно равна нормальной составляющей вектора поляризации численно равна нормальной составляющей вектора поляризации 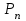 . .8.2. Описание поля в диэлектриках. Рассматривая электростатические явления в пустоте, мы всегда полагали, что заряды обусловлены избытком или недостатком электронов в каждом элементе объема заряженного тела, содержащем достаточно большое число молекул. Заряды такого рода мы назвали свободными. Мы, также, видели, что при поляризации диэлектрика возможно появление связанных зарядов. Связанные заряды появляются только при наличии в диэлектрике электрического поля. Таким образом, первичным источником поля всегда являются свободные заряды. Однако при наличии в поле куска диэлектрика на первичное поле, вызванное свободными зарядами, налагается еще добавочное поле связанных зарядов. Это добавочное поле отлично от нуля как в самом диэлектрике, так, вообще говоря, и вне его. Для того чтобы найти результирующую напряженность поля  , надо сложить напряженность поля свободных зарядов , надо сложить напряженность поля свободных зарядов 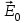 с напряженностью поля связанных зарядов с напряженностью поля связанных зарядов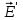 : :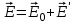 . .Можно показать, что напряженность электрического поля  в однородном диэлектрике, создаваемая рассматриваемыми зарядами при условии, что однородный диэлектрик целиком заполняет все пространство, где поле отлично от нуля, в в однородном диэлектрике, создаваемая рассматриваемыми зарядами при условии, что однородный диэлектрик целиком заполняет все пространство, где поле отлично от нуля, в 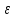 раз меньше напряженности поля раз меньше напряженности поля 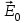 , тех же зарядов в пустоте: , тех же зарядов в пустоте: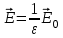 . .Тогда 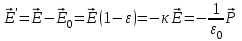 , ,где 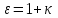 . .Имея дело с электростатическим полем в пустоте, мы вводили в рассмотрение линии напряженности. Линии напряженности в пустоте обладают тем свойством, что они тянутся непрерывно от одних зарядов до других или уходят в бесконечность. Не так обстоит дело в диэлектриках, если учитывать одни только свободные заряды. Например, на границах раздела диэлектриков возникнут связанные поверхностные заряды, и часть линий напряженности будет на них кончаться или с них начинаться. Таким образом, линии напряженности не пройдут непрерывно границу раздела диэлектриков. В соответствии с этим в неоднородных диэлектриках перестает иметь смысл и теорема Остроградского – Гаусса. Можно, однако, ввести для характеристики поля внутри диэлектрика такой новый вектор 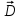 , линии которого пойдут непрерывно в диэлектриках (как однородных, так и неоднородных), а также через границы их раздела. Этот вектор называется вектором электростатической индукции; он связан с вектором напряженности , линии которого пойдут непрерывно в диэлектриках (как однородных, так и неоднородных), а также через границы их раздела. Этот вектор называется вектором электростатической индукции; он связан с вектором напряженности  соотношением: соотношением: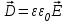 , , где 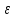 – значение диэлектрической проницаемости в той точке диэлектрика, где определяется значение вектора – значение диэлектрической проницаемости в той точке диэлектрика, где определяется значение вектора 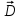 . .Выражение для вектора 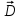 можно дать и в другом виде. По сказанному можно дать и в другом виде. По сказанному 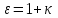 , откуда , откуда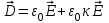 , ,но 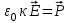 , где , где 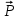 – вектор поляризации. Отсюда получаем – вектор поляризации. Отсюда получаем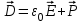 , ,т. е. вектор индукции выражается через сумму вектора напряженности поля  (умноженного на (умноженного на 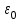 ) и вектора поляризации ) и вектора поляризации 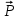 . . Вектор индукции 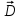 направлен в каждой данной точке так же, как и вектор напряженности направлен в каждой данной точке так же, как и вектор напряженности  , но по численному значению он в , но по численному значению он в 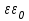 раз больше напряженности. раз больше напряженности. Линии вектора индукции строят тем же способом, каким мы строили в пустоте линии вектора напряженности. Линией вектора индукции называется линия, направление касательной в каждой точке которой совпадает с направлением вектора индукции. Направление самой линии считается совпадающей в каждой точке с направлением вектора индукции в этой точке. Вопросы для самоконтроля. 1. Какие вещества называют диэлектриками? 2. Какие два основных вида диэлектриков существует? 3. Какая система зарядов называется электрическим диполем? Каким параметром она характеризуется? 4. Что происходит с неполярными молекулами диэлектриков во внешнем электрическом поле? 5. Как действует электрическое поле на полярные молекулы? 6. В чем состоит различие в поляризации диэлектриков с полярными и неполярными молекулами? 7. Каков физический смысл вектора поляризации? 8. Найдите связь между векторами электрического смещения, напряженности поля и поляризации. 9. Найдите связь между относительной диэлектрической проницаемостью среды и ее диэлектрической восприимчивостью. Лекция № 9. Энергия электростатического поля. Цель: определить энергию различных электрических систем, определить энергию и плотность энергии электростатического поля. Основные понятия: Однородное электростатическое поле – поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства. Плотность энергии электростатического поля – количество энергии приходящееся на единицу объема, заполняемого полем. 9.1. Энергия системы зарядов. Силы, с которыми взаимодействуют заряженные тела, консервативны (их работа не зависит от пути). Следовательно, система заряженных тел обладает потенциальной энергией. Найдем выражение для потенциальной энергии системы точечных зарядов. Начнем с системы из двух зарядов q1и q2, находящихся на расстоянии r12. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние r12. При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q1и q2, либо q2 к q1. В обоих случаях совершается одинаковая работа. Работа переноса заряда q1 из бесконечности в точку, удаленную от q2 на r12 равна 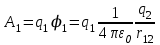 , ,где 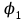 - потенциал, создаваемый зарядом q2 в той точке, в которую перемещается заряд q1. - потенциал, создаваемый зарядом q2 в той точке, в которую перемещается заряд q1. Аналогично работа переноса заряда q2 из бесконечности в точку, удаленную от q1 на r12, равна 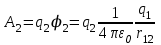 , ,где 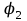 – потенциал, создаваемый зарядом q1 в той точке, в которую перемещается заряд q2. – потенциал, создаваемый зарядом q1 в той точке, в которую перемещается заряд q2.Значения работ 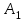 и и 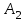 одинаковы, и каждое из них выражает энергию системы одинаковы, и каждое из них выражает энергию системы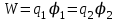 . .Для того чтобы в выражение энергии системы оба заряда входили симметрично, напишем его следующим образом: 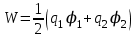 . .Данная формула дает энергию системы двух зарядов. В случае N зарядов потенциальная энергия системы равна 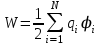 , ,где 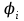 – потенциал, создаваемый в той точке, где находится qi, всеми зарядами, кроме i-го. – потенциал, создаваемый в той точке, где находится qi, всеми зарядами, кроме i-го.9.2. Энергия заряженного проводника. Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов 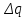 . Согласно сказанному выше, такая система обладает энергией, равной работе, которую нужно совершить, чтобы перенести все заряды . Согласно сказанному выше, такая система обладает энергией, равной работе, которую нужно совершить, чтобы перенести все заряды 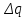 из бесконечности и расположить на поверхности проводника. из бесконечности и расположить на поверхности проводника. Перенос из бесконечности на поверхность проводника первой порции заряда 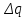 не сопровождается совершением работы, так как потенциал проводника первоначально равен нулю. В результате сообщения проводнику заряда не сопровождается совершением работы, так как потенциал проводника первоначально равен нулю. В результате сообщения проводнику заряда 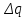 его потенциал становится отличным от нуля, вследствие чего перенос второй порции его потенциал становится отличным от нуля, вследствие чего перенос второй порции 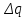 уже требует совершения некоторой работы. Так как по мере увеличения заряда на проводнике потенциал его растет, при перемещении каждой последующей порции заряда уже требует совершения некоторой работы. Так как по мере увеличения заряда на проводнике потенциал его растет, при перемещении каждой последующей порции заряда 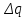 должна совершаться все большая по величине работа должна совершаться все большая по величине работа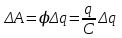 , ,где 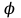 – потенциал проводника, обусловленный уже имеющимся на нем зарядом q, С – емкость проводника. – потенциал проводника, обусловленный уже имеющимся на нем зарядом q, С – емкость проводника. Работа 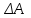 идет на увеличение энергии проводника. Поэтому, переходя к дифференциалам, имеем идет на увеличение энергии проводника. Поэтому, переходя к дифференциалам, имеем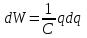 , ,откуда получается выражение для энергии: 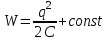 . .Естественно считать энергию незаряженного проводника равной нулю. Тогда const также обращается в нуль. Учтя соотношение между емкостью, зарядом и потенциалом проводника, можно написать 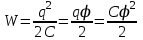 . .9.3. Энергия заряженного конденсатора. Процесс возникновения на обкладках конденсатора зарядов +q и -q можно представить так, что от одной обкладки последовательно отнимаются очень малые порции заряда 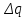 и перемещаются на другую обкладку. Работа переноса очередной порции равна и перемещаются на другую обкладку. Работа переноса очередной порции равна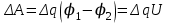 , ,где U – напряжение на конденсаторе. Заменяя U в соответствии с формулой для емкости конденсатора и переходя к дифференциалам, получим 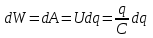 . .Наконец, интегрируя последнее выражение, приходим к формуле для энергии заряженного конденсатора 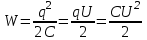 . .9.4. Энергия электростатического поля. Энергию конденсатора теперь можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это для плоского конденсатора: 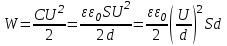 . .Данная формула связывает энергию конденсатора с зарядом на его обкладках. Произведение Sd – объем V, занимаемый полем; 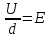 . Т. о, можно написать . Т. о, можно написать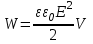 . . Данная формула связывает энергию конденсатора с напряженностью поля. Логично поставить вопрос: где же локализована (т. е. сосредоточена) энергия, что является носителем энергии – заряды или поле? Экспериментальные факты говорят о том, что носителем энергии является поле. Если поле однородно, т. е. если его напряженность одинакова по модулю и направлению в любой точке пространства (что имеет место в плоском конденсаторе), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w, равной энергии поля, деленной на заполняемой полем объем. Следовательно, плотность энергии электростатического поля 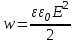 . .Данная формула справедлива и для неоднородного поля. Эту формулу можно, также, записать в виде 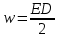 , ,или 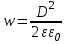 . .Вопросы для самоконтроля. 1. Чему равна энергия системы электрических зарядов? 2. Приведите выражение для энергии заряженного проводника. 3. Приведите выражение энергии заряженного конденсатора. 4. Где сосредоточена электрическая энергия? 4. Чему равна объемная плотность энергии электростатического поля? ЛИТЕРАТУРА Бутиков Е. И., Кондратьев А. С. Физика для углубленного изучения, т. 2. Электродинамика. Оптика. М., 2004 г. Васильев А. Э. Курс общей физики. Электричество и магнетизм. СПб., 2003 г. Гершензон Е. М., Малов Н. Н., Мансуров А. Н. Электродинамика. М., 2002 г. Калашников С. Г. Электричество. М., 2003 г. Огурцов А. Н. Лекции по физике. Электричество. М., 2004 г. Ревинская О.Г., Кравченко Н. С. Электростатическое поле. Томск, 2014 г. Дмитриева В. Ф. Физика. М., 2005 г. |
