конспект. КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальносте. Конспект лекций по физике для студентов 12 курсов специальностей технического профиля спо раздел Электростатика Ейск, 2017
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Тема 4. Электростатическое поле при наличии проводников и диэлектриков. Энергия электростатического поля Лекция № 7. Электростатическое поле при наличии проводников. Цель: рассмотреть свойства проводников в электростатическом поле, сформировать понятие «электроемкость». Основные понятия: Проводник – вещество, содержащие свободные заряженные частицы. Электростатическая индукция – появление электрических зарядов разного знака на противоположных участках поверхности проводника при внесении его в электростатическое поле. Электроемкость проводника – физическая величина, численно равная заряду, который надо сообщить ранее не заряженному проводнику, чтобы потенциал его принял значение, равное единице. Конденсатор – система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Электроемкость конденсатора – физическая величина, численно равная заряду, который надо сообщить конденсатору для изменения разности потенциалов на его обкладках на единицу. 7.1. Равновесие зарядов на проводнике. Проводниками называют вещества, содержащие свободные заряженные частицы. Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому равновесие зарядов на проводнике может наблюдаться лишь при выполнении следующих условий: 1. Напряженность поля всюду внутри проводника должна быть равна нулю 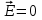 . .Но т. к. 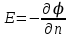 , то это означает, что потенциал внутри проводника должен быть постоянным ( , то это означает, что потенциал внутри проводника должен быть постоянным (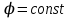 ). ). 2. Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности 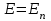 . .(Если 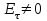 на поверхности, то будет существовать движение зарядов по поверхности). Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной. на поверхности, то будет существовать движение зарядов по поверхности). Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной. Если проводящему телу сообщить некоторый заряд q, то он распределится так, чтобы соблюдались условия равновесия. При равновесии ни в каком месте внутри проводника не может быть избыточных зарядов – все они расположатся по поверхности проводника с некоторой плотностью 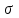 . . Так как в состоянии равновесия внутри проводника избыточных зарядов нет, удаление вещества из некоторого объема, взятого внутри проводника, никак не отразится на равновесном расположении зарядов. Таким образом, избыточный заряд распределяется на полом проводнике так же, как и на сплошном, т. е. по его наружной поверхности. На поверхности полости в состоянии равновесия избыточные заряды располагаться не могут. Этот вывод вытекает также из того, что одноименные элементарные заряды, образующие данный заряд q, взаимно отталкиваются и, следовательно, стремятся расположиться на наибольшем расстоянии друг от друга. Р 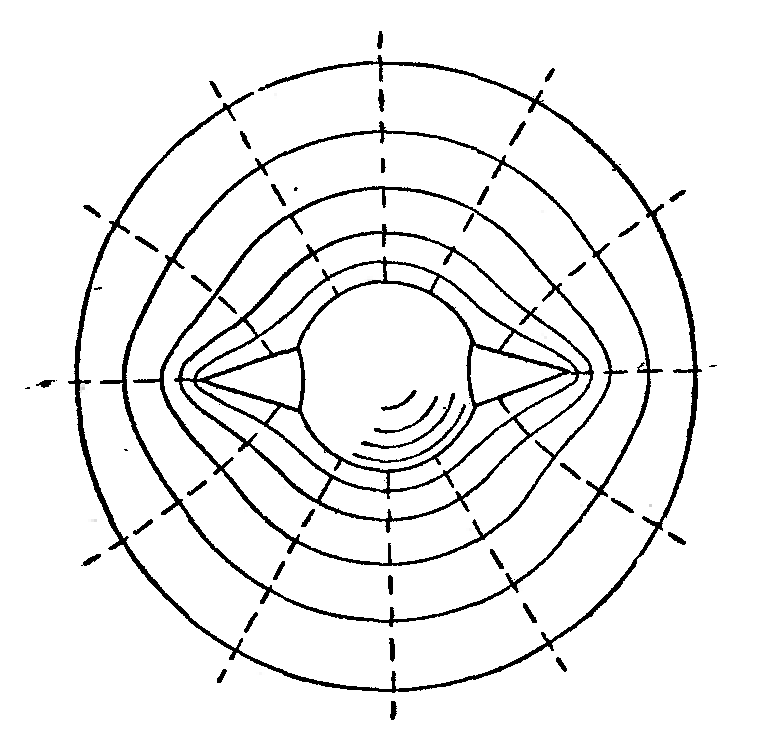 ассмотрим поле, создаваемое изображенным на рисунке заряженным проводником. На больших расстояниях от проводника эквипотенциальные поверхности имеют характерную для точечного заряда форму сферы. По мере приближения к проводнику эквипотенциальные поверхности становятся все более сходными с поверхностью проводника, которая, как мы знаем, является эквипотенциальной. Вблизи выступов эквипотенциальные поверхности располагаются гуще, значит и напряженность поля здесь больше. Но т. к. вблизи поверхности проводника ассмотрим поле, создаваемое изображенным на рисунке заряженным проводником. На больших расстояниях от проводника эквипотенциальные поверхности имеют характерную для точечного заряда форму сферы. По мере приближения к проводнику эквипотенциальные поверхности становятся все более сходными с поверхностью проводника, которая, как мы знаем, является эквипотенциальной. Вблизи выступов эквипотенциальные поверхности располагаются гуще, значит и напряженность поля здесь больше. Но т. к. вблизи поверхности проводника 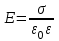 (- относительная диэлектрическая проницаемость среды, окружающей проводник), то получается, что плотность зарядов на выступах особенно велика. К тому же выводу можно прийти, учитывая, что из-за взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга. (- относительная диэлектрическая проницаемость среды, окружающей проводник), то получается, что плотность зарядов на выступах особенно велика. К тому же выводу можно прийти, учитывая, что из-за взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга. В 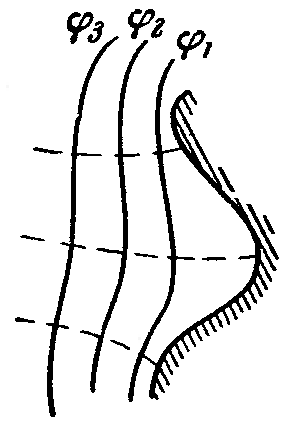 близи углублений в проводнике эквипотенциальные поверхности расположены реже. Соответственно напряженность поля и плотность зарядов в этих местах будет меньше. Вообще, плотность зарядов при данном потенциале проводника определяется кривизной поверхности — она растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости). Особенно велика бывает плотность зарядов на остриях. Поэтому напряженность поля вблизи остриев может быть настолько большой, что происходит ионизация молекул газа, окружающего проводник. Ионы иного знака, чем q, притягиваются к проводнику и нейтрализуют его заряд. Ионы того же знака, что и q, начинают двигаться от проводника, увлекая с собой нейтральные молекулы газа. В результате возникает ощутимое движение газа, называемое электрическим ветром. Заряд проводника уменьшается, он как бы стекает с острия и уносится ветром. Поэтому такое явление называют истечением заряда с острия. близи углублений в проводнике эквипотенциальные поверхности расположены реже. Соответственно напряженность поля и плотность зарядов в этих местах будет меньше. Вообще, плотность зарядов при данном потенциале проводника определяется кривизной поверхности — она растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости). Особенно велика бывает плотность зарядов на остриях. Поэтому напряженность поля вблизи остриев может быть настолько большой, что происходит ионизация молекул газа, окружающего проводник. Ионы иного знака, чем q, притягиваются к проводнику и нейтрализуют его заряд. Ионы того же знака, что и q, начинают двигаться от проводника, увлекая с собой нейтральные молекулы газа. В результате возникает ощутимое движение газа, называемое электрическим ветром. Заряд проводника уменьшается, он как бы стекает с острия и уносится ветром. Поэтому такое явление называют истечением заряда с острия. 7.2. Проводник во внешнем электрическом поле. При внесении незаряженного проводника в электрическое поле носители заряда приходят в движение: положительные в направлении вектора  , отрицательные – в противоположную сторону. В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами. Поле этих зарядов направлено противоположно внешнему полю. Таким образом, накапливание зарядов у концов проводника приводит к ослаблению в нем поля. Перераспределение носителей заряда происходит до тех пор, пока не б , отрицательные – в противоположную сторону. В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами. Поле этих зарядов направлено противоположно внешнему полю. Таким образом, накапливание зарядов у концов проводника приводит к ослаблению в нем поля. Перераспределение носителей заряда происходит до тех пор, пока не б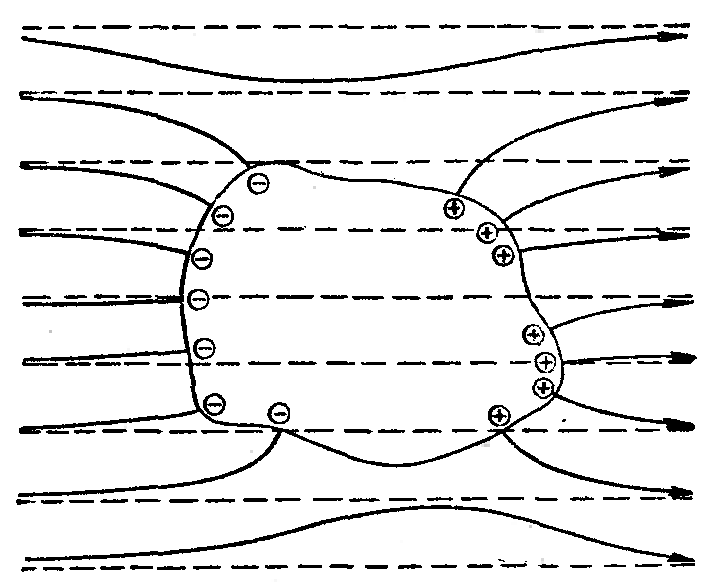 удут выполнены условия равновесия зарядов на проводнике, т, е. пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника перпендикулярными к его поверхности. Следовательно, нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности – они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. удут выполнены условия равновесия зарядов на проводнике, т, е. пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника перпендикулярными к его поверхности. Следовательно, нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности – они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются по внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также обращается в нуль. На этом основывается электростатическая защита. Когда какой-то прибор хотят защитить от воздействия внешних полей, его окружают проводящим футляром (экраном). Внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Подобный экран действует хорошо и в том случае, если его сделать не сплошным, а в виде густой сетки. Н 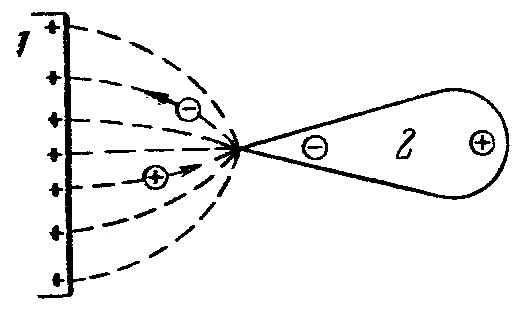 аличие острия у проводящего тела может приводить не только к стеканию зарядов с него, но и к «натекание» на проводник зарядов с других тел. Под действием поля, создаваемого заряженным телом 1, на теле 2 возникают индуцированные заряды. Сильное поле, создаваемое вблизи острия находящимся на нем индуцированным зарядом, ионизует молекулы газа. Ионы разных знаков движутся в противоположные стороны и оседают на соответствующих телах. В результате заряд q тела 1 уменьшается, а на проводнике с острием накапливается заряд, одноименный с q. Заряд как бы переходит от заряженного тела 1 к первоначально незаряженному телу 2. аличие острия у проводящего тела может приводить не только к стеканию зарядов с него, но и к «натекание» на проводник зарядов с других тел. Под действием поля, создаваемого заряженным телом 1, на теле 2 возникают индуцированные заряды. Сильное поле, создаваемое вблизи острия находящимся на нем индуцированным зарядом, ионизует молекулы газа. Ионы разных знаков движутся в противоположные стороны и оседают на соответствующих телах. В результате заряд q тела 1 уменьшается, а на проводнике с острием накапливается заряд, одноименный с q. Заряд как бы переходит от заряженного тела 1 к первоначально незаряженному телу 2.7.3. Электроемкость проводников. Перейдем к рассмотрению весьма важного свойства проводников, называемого их электроемкостью или просто емкостью. Опыт показывает, что разные проводники, будучи заряжены одинаковым количеством электричества, принимают разные потенциалы; это указывает, что они отличаются друг от друга физическим свойством, которое характеризуется величиной, называемой емкостью. Емкость проводника зависит от расположения окружающих тел, т. к. окружающие тела (даже нейтральные) могут электризоваться (посредством индукции) и менять поле вокруг проводника, а, следовательно, и распределение зарядов на проводнике (что ведет к изменению поля, создаваемого зарядами проводника, и, следовательно, к изменению потенциала, зависящего от данного поля). Потому сперва определим понятие емкости уединенного проводника, т. е. такого проводника, вблизи которого нет никаких других тел, которые могли бы повлиять на распределение на нем зарядов. Потенциал уединенного проводника 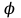 пропорционален величине заряда q, так как при увеличении заряда в определенное число раз увеличивается в такое же число раз напряженность поля, а, следовательно, и работа перемещения заряда от проводника в бесконечность: пропорционален величине заряда q, так как при увеличении заряда в определенное число раз увеличивается в такое же число раз напряженность поля, а, следовательно, и работа перемещения заряда от проводника в бесконечность: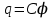 . .Коэффициент пропорциональности С зависит от формы и величины проводника и называется его емкостью. Из последнего равенства имеем: 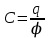 . .Это соотношение указывает, что емкость уединенного проводника есть физическая величина, численно равная количеству электричества, которое надо сообщить ранее не заряженному проводнику, чтобы потенциал его принял значение, равное единице (при 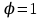 имеем имеем 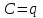 ). При этом мы считаем, что неопределенная постоянная в выражении потенциала выбрана так, что потенциалы бесконечно удаленных от проводника точек равны нулю. ). При этом мы считаем, что неопределенная постоянная в выражении потенциала выбрана так, что потенциалы бесконечно удаленных от проводника точек равны нулю.В системе СИ за единицу емкости принято брать емкость такого проводника, увеличение на котором заряда на один кулон ведет к повышению его потенциала на один вольт. Такая единица называется фарадой. Очевидно, фарада есть чрезвычайно большая единица емкости. В самом деле, это есть емкость уединенного шара радиусом 9 миллионов километров (в 1400 раз большим радиуса земного шара). Практически поэтому наряду с единицей емкости фарадой употребляют меньшую, называемую микрофарадой, равную одной миллионной доле фарады. Емкостью в одну микрофараду обладает уединенный шар радиусом 9 км, т. е. тоже еще очень большой шар. Емкость проводника зависит от окружающих данный проводник тел. Действительно, под емкостью проводника мы подразумеваем физическую величину, измеряемую отношением заряда проводника к его потенциалу, потенциал же проводника зависит не только от заряда на нем самом, но и от зарядов всех тел, окружающих его. Если даже окружающие данный проводник тела и не были предварительно заряжены, то при заряжении рассматриваемого проводника они зарядятся через слияние и, таким образом, изменят потенциал на данном проводнике. В этом случае понятие емкости естественно обобщить, введя следующее определение, пригодное и в динамических задачах: 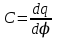 ; ;емкость определяется по отношению приращения заряда проводника к приращению его потенциала при стремлении этих приращений к нулю, т. е. как производная заряда проводника по его потенциалу. 7.4. Конденсаторы. У 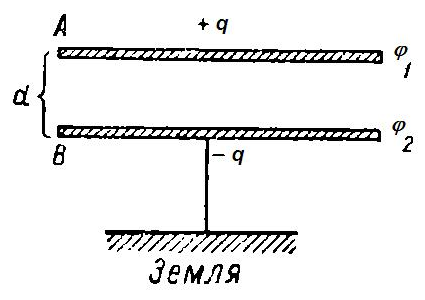 единенные проводники обладают малой емкостью. Даже шар таких размеров, как Земля, имеет емкость всего лишь 700 микрофарад. Вместе с тем на практике бывает потребность в осуществлении системы проводников с большой емкостью, практически не зависящей от окружающих тел. Это оказывается возможным, если система защищена от влияния прочих тел. Примером таких систем являются конденсаторы. единенные проводники обладают малой емкостью. Даже шар таких размеров, как Земля, имеет емкость всего лишь 700 микрофарад. Вместе с тем на практике бывает потребность в осуществлении системы проводников с большой емкостью, практически не зависящей от окружающих тел. Это оказывается возможным, если система защищена от влияния прочих тел. Примером таких систем являются конденсаторы. Так называемый плоский конденсатор состоит из двух параллельных пластин А и В, расположенных друг от друга на расстоянии d, малом по сравнение с их собственными размерами. Будем считать, что между пластинами – пустота (практически это может быть воздух). Пусть пластина В соединена с землей. Если другой пластине А сообщить заряд +q, то благодаря электростатической индукции на пластине В возникает заряд -q (равный ему заряд +q отводится к земле и роли не играет). Пластина В, соединенная с землей, принимает потенциал Земли, который мы обозначим через 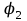 Тогда пластина А примет некоторый потенциал Тогда пластина А примет некоторый потенциал 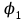 значение которого определится лишь величиной заряда q и потенциалом значение которого определится лишь величиной заряда q и потенциалом 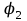 пластины В. Другие незаряженные тела не будут влиять на потенциал пластины В. Другие незаряженные тела не будут влиять на потенциал 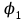 и, следовательно, на емкость конденсатора С, так как поле зарядов +q и -q сосредоточено лишь между пластинами А и В и поэтому не может вызывать на других внешних телах индуцированные заряды. и, следовательно, на емкость конденсатора С, так как поле зарядов +q и -q сосредоточено лишь между пластинами А и В и поэтому не может вызывать на других внешних телах индуцированные заряды. Под емкостью С конденсатора подразумевается величина, измеряемая отношением заряда на одной из пластин (положительной) к разности потенциалов между пластинами: 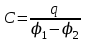 , ,где считаем 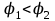 . .Выразим емкость плоского конденсатора через величины, характеризующие его размеры. Так как размеры пластин велики по сравнению с расстоянием между ними, то напряженность поля между пластинами такая же, как и в случае двух бесконечных плоскостей, несущих равные по численному значению заряды противоположных знаков. Тогда имеем, что напряженность поля между пластинами E равна: 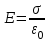 , ,где 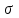 - поверхностная плотность зарядов. Обозначим площадь одной пластины через S, тогда - поверхностная плотность зарядов. Обозначим площадь одной пластины через S, тогда 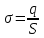 и и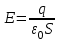 , ,откуда: 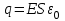 . .Напряженность поля Е выразим через разность потенциалов 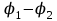 : : 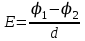 . . Тогда найдем: 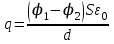 Воспользовавшись этим равенством и формулой для емкости плоского конденсатора С получим: 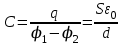 . .Из последней формулы видно, что емкость плоского конденсатора пропорциональна площади пластины S и обратно пропорциональна расстоянию между пластинами d. Чем ближе расположены пластины друг к другу, тем больше емкость образуемого ими конденсатора. Если пространство между пластинами заполнить какой-либо непроводящей (диэлектрической) средой с относительной диэлектрической проницаемостью , то емкость плоского конденсатора увеличится в раз: 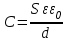 . .Приведем без вывода формулы для нахождения емкостей цилиндрического и сферического конденсаторов. Для цилиндрического конденсатора: 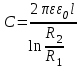 , ,где l – длина цилиндрических обкладок, R1 и R2- радиусы внутренней и внешней обкладок конденсатора, соответственно. Если между обкладками конденсатора находится воздух, то полагаем =1. Для сферического конденсатора: 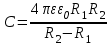 , ,где R1 и R2 – радиусы внутренней и внешней обкладок конденсатора, соответственно. Если между обкладками конденсатора находится воздух, то полагаем =1. Вопросы для самоконтроля. 1. Какие вещества называют проводниками? 2. Каковы напряженность и потенциал поля, а также распределение зарядов внутри и на поверхности заряженного проводника. 3. В чем состоит электростатическая защита? 4. Что называется электроемкостью уединенного проводника и от чего она зависит? 5. Что называется электроемкостью конденсатора и от чего она зависит? 6. Чему равна электроемкость плоского, цилиндрического и сферического конденсатора? Лекция № 8. Электростатическое поле при наличии диэлектриков. Цель: рассмотреть свойства диэлектриков в электростатическом поле. Основные понятия: Диэлектрик – вещество, не содержащее свободных заряженных частиц. Диполь – система равных по величине, но противоположных по знаку двух точечных зарядов, сдвинутых друг относительно друга на некоторое расстояние. Дипольный момент – векторная величина, характеризующая асимметрию распределения положительного и отрицательного зарядов в электрически нейтральной системе. Поляризация – возникновение суммарного, отличного от нуля, дипольного момента молекул диэлектрика при внесении его в электростатическое поле. Вектор электростатической индукции – силовая характеристика электростатического поля, учитывающая поляризованность среды; его единственным источником являются свободные заряды. |
