|
|
конспект. КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальносте. Конспект лекций по физике для студентов 12 курсов специальностей технического профиля спо раздел Электростатика Ейск, 2017
Министерство образования, науки и молодежной политики Краснодарского края
ГБПОУ КК «Колледж Ейский»
КОНСПЕКТ ЛЕКЦИЙ
по физике
для студентов 1-2 курсов специальностей технического профиля СПО
Раздел 1. Электростатика
Ейск, 2017
Конспект лекций по физике состоит из трех разделов, в которых в доступной форме излагаются физические основы электродинамики, нацелен на систематизацию и конкретизацию знаний, приобретенных в процессе изучения учебной дисциплины Физика, и содержит материал, достаточный для успешного прохождения студентами текущей и промежуточной аттестации.
Конспект лекций подготовлен согласно тематике рабочей программы учебной дисциплины и включает широкий спектр вопросов для самоконтроля.
Разработчик: преподаватель ГБПОУ КК «Колледж Ейский» Л.С.Черных
СОДЕРЖАНИЕ
Тема 1. Электростатическое поле. Закон Кулона
Лекция 1. Электростатическое поле 4
Лекция 2. Закон Кулона 7
Тема 2. Напряженность электростатического поля
Лекция 3. Напряженность электростатического поля точечного
заряда 11
Лекция 4. Принцип суперпозиции полей. Напряженность поля заряженной нити, плоскости, шара 12
Тема 3. Потенциальность электростатического поля
Лекция 5. Работа сил электростатического поля 19
Лекция 6. Потенциал электростатического поля 21
Тема 4. Электростатическое поле при наличии проводников и диэлектриков. Энергия электростатического поля
Лекция 7. Электростатическое поле при наличии проводников 28
Лекция 8. Электростатическое поле при наличии диэлектриков 35
Лекция 9. Энергия электростатического поля 40
Литература 44
Электростатика
Тема 1. Электростатическое поле. Закон Кулона
Лекция № 1. Электростатическое поле.
Цель: ознакомиться с понятиями «электростатическое поле» и «электрический заряд», изучить их свойства.
Основные понятия:
Электрический заряд – некоторое внутреннее, первичное свойство частицы.
Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макроскопически заряженными телами.
Электромагнитное поле – особый вид материи.
Электростатическое поле – частный случай электромагнитного поля неподвижных электрических зарядов.
1.1. Электрический заряд и его свойства.
Уже в глубокой древности было известно, что янтарь, потертый о шерсть, приобретает способность притягивать легкие предметы. Однако только в конце XVI века английский врач Гильберт подробно исследовал это явление и нашел, что аналогичным свойством обладают многие другие вещества. Тела, способные, подобно янтарю, после натирания притягивать легкие предметы, он назвал наэлектризованными (от греческого электрон – янтарь). Теперь мы говорим, что на телах в таком состоянии имеются электрические заряды, а сами эти тела называем заряженными.
Укажем, что само трение при «электризации трением» не играет никакой принципиальной роли. Электрические заряды всегда возникают при тесном соприкосновении различных веществ.
Опыт показывает, далее, что два заряженных тела могут либо отталкиваться, либо притягиваться друг к другу. Если зарядить два легких тела, подвешенных на изолирующих шелковых нитях, прикасаясь к ним стеклянной палочкой, потертой о шелк, то оба тела отталкиваются. То же наблюдается, если оба тела заряжены при помощи эбонитовой палочки, потертой о мех. Но если зарядить одно из тел от стеклянной палочки, а другое – от эбонитовой, то оба тела притягиваются друг к другу. Это означает, что заряды стекла и эбонита качественно различны.
Несмотря на обилие различных веществ в природе, существуют только два вида электрических зарядов: заряды, подобные возникающим на стекле, потертом о шелк, и заряды, подобные появляющимся на эбоните, потертом о мех. Первые из них получили название положительных зарядов, а вторые - отрицательных зарядов. Следовательно, одноименные заряды отталкиваются, а разноименные притягиваются.
Рассмотренные выше притяжения и отталкивания между заряженными телами являются частными случаями электромагнитных взаимодействий. В настоящее время известно, что в основе всего разнообразия явлений природы лежат всего четыре фундаментальных взаимодействия между элементарными частицами – сильное, слабое, электромагнитное и гравитационное. Каждый вид взаимодействия связывается с определенной характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц. Электромагнитное взаимодействие зависит от одной из основных, первичных характеристик частицы - электрического заряда.
Электрическому заряду частицы присущи следующие фундаментальные свойства:
1) существует элементарный (минимальный) электрический заряд e=1,6⋅10–19 Кл (кулон (Кл) – единица электрического заряда в системе СИ).
2) электрический заряд существует в двух видах – положительный (носитель элементарного положительного заряда – протон, его масса mp =1,67⋅10–27 кг) и отрицательный (носитель элементарного отрицательного заряда – электрон, его масса me =9,11⋅10–31 кг).
3) одноименные заряды отталкиваются, разноименные – притягиваются.
4) электрический заряд является релятивистским инвариантом – его величина не зависит от системы отсчета, а, значит, не зависит от скорости заряженной частицы.
5) электрический заряд дискретен – заряд любого тела составляет целое кратное от элементарного электрического заряда e.
6) электрический заряд аддитивен – заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему).
7) электрический заряд подчиняется закону сохранения заряда: алгебраическая сумма электрических зарядов любой электрически изолированной системы остается неизменной, какие бы процессы ни происходили внутри данной системы. Под электрически изолированной системой в данном случае понимают систему, которая не обменивается зарядами с внешними телами.
Электромагнитные взаимодействия изучает раздел физики, называемый электродинамикой.
Взаимодействие между неподвижными электрически заряженными частицами или телами изучается электростатикой - разделом электродинамики. При исследовании взаимодействия электрических зарядов, естественно, возникает вопрос, почему появляются силы, действующие на заряды, и как они передаются от одного заряда к другому? Совершенно так же можно поставить и следующий вопрос: механические силы возникают только при наличии двух зарядов; происходят ли, однако, какие-либо изменения в окружающем пространстве при наличии только одного заряда, когда второго нет вовсе?
В процессе развития физики существовали два противоположных подхода к ответу на поставленные вопросы. При одном из них предполагалось, что телам присуще свойство действовать на другие тела на расстоянии, без участия промежуточных тел или среды, т.е. предполагалось, что силы могут передаваться от одного тела к другому через пустоту и притом мгновенно (теории дальнодействия). С этой точки зрения при наличии только одного заряда никаких изменений в окружающем пространстве не происходит.
Согласно второму взгляду силовые взаимодействия между разобщенными телами могут передаваться только при наличии какой-либо среды, окружающей эти тела, последовательно от одной части этой среды к другой, и с конечной скоростью (теории близкодействия); даже при наличии одного-единственного заряда в окружающем пространстве происходят определенные изменения.
Современная физика сохраняет только идею близкодействия и отвергает дальнодействие. Действительно, допущение возможности передачи силовых взаимодействий, т.е. движения, через пустоту, без участия материи, равносильно допущению возможности движения без материи, что бессодержательно.
Таким образом, для понимания происхождения и передачи сил, действующих между покоящимися зарядами, необходимо допустить наличие между зарядами какого-то физического агента, осуществляющего это взаимодействие. Этим агентом и является электрическое поле. Когда в каком-либо месте появляется электрический заряд, то вокруг него возникает электрическое поле. Основное свойство электрического поля заключается в том, что на всякий другой заряд, помещенный в это поле, действует сила.
Т. о., рассматривая взаимодействие покоящихся зарядов, мы приходим к понятию электростатического поля. Оно представляет собой стационарное, т. е. не изменяющееся с течением времени, электрическое поле неподвижных электрических зарядов. Это поле является частным случаем электромагнитного поля, посредством которого осуществляется взаимодействие между электрически заряженными частицами, движущимися в общем случае произвольным образом относительно системы отсчета.
Электростатическое поле (как и в общем случае электромагнитное) заключает в себе определенную энергию, обладает массой и, следовательно, не является некоторой абстракцией, введенной нами для описания электрических взаимодействий, но представляет собой объективную реальность, обладающую физическими свойства. Оно является определенной формой материи, которая осуществляет электрические взаимодействия. Таким образом, современная физика при помощи понятия поля расширяет представление о близкодействии и распространяет его на немеханические явления.
Вопросы для самоконтроля:
1. Какие типы фундаментальных взаимодействий вы знаете?
2. Какое взаимодействие называют электромагнитным?
3. Что изучает электростатика?
4. Что представляет собой электрический заряд?
5. Перечислите свойства электрического заряда.
6. Сформулируйте закон сохранения зарядов.
7. Как называется единица электрического заряда?
8. Чему равно значение элементарного заряда?
9. В чем сущность теорий дальнодействия и близкодействия?
Лекция № 2. Закон Кулона.
Цель: изучить закон взаимодействия двух неподвижных точечных зарядов.
Основные понятия:
Точечный заряд – протяженное заряженное тело, размеры которого малы по сравнению с расстоянием от других зарядов.
Закон Кулона – основной закон электростатического взаимодействия точечных зарядов.
Начало количественного изучения электрических явлений относится к концу XVIII века, когда Кулон установил на опыте закон взаимодействия электрических зарядов.
Для заряженных тел произвольных размеров такой закон в общей форме дать нельзя, так как сила взаимодействия протяженных тел зависит от их формы и взаимного расположения. Однако форма тел и их взаимная ориентировка перестают сказываться, если размеры тел весьма малы по сравнению с расстоянием между ними. Поэтому закон взаимодействия, имеющий общее значение, можно установить только для точечных зарядов.
Так как электрические заряды всегда распределены в объеме, то никаких конечных зарядов в математической точке, разумеется, быть не может. Под точечным зарядом в физике всегда понимают протяженное заряженное тело, размеры которого весьма малы по сравнению с расстоянием от других зарядов.
Ш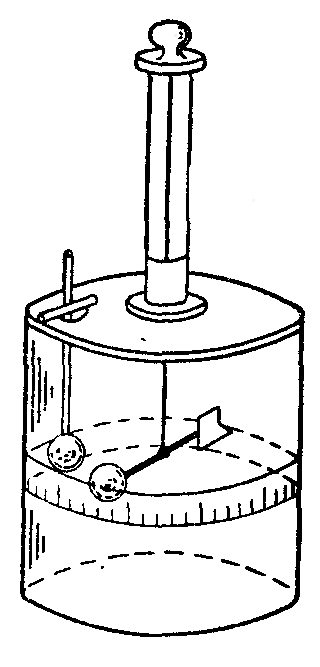 . Кулон проводил эксперименты с помощью крутильных весов. По углу закручивания упругой нити он измерял силу отталкивания одноименно заряженных шариков, а по шкале прибора – расстояние между ними. В результате этих опытов Кулон заключил, что сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, и обратно пропорциональна квадрату расстояния между зарядами: . Кулон проводил эксперименты с помощью крутильных весов. По углу закручивания упругой нити он измерял силу отталкивания одноименно заряженных шариков, а по шкале прибора – расстояние между ними. В результате этих опытов Кулон заключил, что сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, и обратно пропорциональна квадрату расстояния между зарядами:
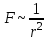 . .
Никаких способов измерения величины электрических зарядов в то время еще не было. Однако это не помешало Кулону найти вид зависимости силы F от q1 и q2. Он использовал следующий факт: если заряженный проводящий шарик привести в соприкосновение с точно таким же незаряженным шариком, то заряд первого равномерно распределится между обоими шариками. Иными словами, заряд каждого из них будет вдвое меньше исходного. Точно так же можно уменьшить заряд шарика в четыре, восемь раз и т. д. Таким образом, не зная абсолютных значений зарядов q1 и q2, их можно уменьшать в известное число раз.
Опыты, поставленные Кулоном, показали, что при постоянных r и q1 сила взаимодействия F между заряженными шариками изменяется пропорционально величине заряда q2 второго шарика, а при постоянных r и q2 – пропорционально величине заряда q1 первого шарика. Этим было доказано, что сила F пропорциональна произведению q1 q2.
Т. о., сила взаимодействия двух точечных зарядов в вакууме равна
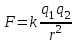
Здесь k — коэффициент пропорциональности, зависящий от выбора единиц заряда, расстояния и силы.
Закон Кулона в системе единиц СИ записывают в виде
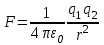 , ,
где вместо коэффициента пропорциональности k, написано 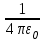 , где , где 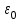 = 8,85·10-12 Кл2/(Н·м2) – электрическая постоянная. = 8,85·10-12 Кл2/(Н·м2) – электрическая постоянная.
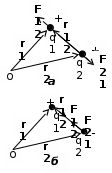 Для того чтобы выразить не только модуль силы, но и ее направление, закон Кулона можно представить в векторной форме: Для того чтобы выразить не только модуль силы, но и ее направление, закон Кулона можно представить в векторной форме:
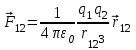 , ,
где 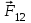 — вектор силы, действующей на заряд 1 со стороны заряда 2, а — вектор силы, действующей на заряд 1 со стороны заряда 2, а 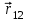 — радиус-вектор, направленный от заряда 2 к заряду 1 (рис. а и б). — радиус-вектор, направленный от заряда 2 к заряду 1 (рис. а и б).
Соответственно сила 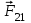 , действующая на заряд 2 со стороны заряда 1, равна , действующая на заряд 2 со стороны заряда 1, равна
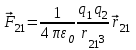 , ,
где 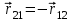 - радиус-вектор, направленный от заряда 1 к заряду 2. - радиус-вектор, направленный от заряда 1 к заряду 2.
Если взаимодействие происходит не в вакууме, то закон Кулона имеет вид:
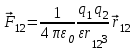 , ,
где 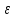 - относительная диэлектрическая проницаемость среды. - относительная диэлектрическая проницаемость среды.
Еще раз отметим, что закон Кулона справедлив только для взаимодействия точечных электрических зарядов, т.е. таких заряженных тел, линейными размерами которых можно пренебречь по сравнению с расстоянием между ними. Кроме того, он выражает силу взаимодействия между неподвижными зарядами, т.е. это закон электростатический. Закон Кулона можно сформулировать следующим образом: сила электростатического взаимодействия между двумя точечными электрическими зарядами пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды притягиваются, а разноименные отталкиваются.
Всякое заряженное тело можно рассматривать как совокупность точечных зарядов аналогично тому, как в механике всякое тело можно считать совокупностью материальных точек. Поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равна векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.
Расчеты показывают, что закон Кулона справедлив также и для взаимодействия заряженных тел шарообразной формы, если заряды q1 и q2 распределены равномерно по всему объему или по всей поверхности этих тел. При этом радиусы тел могут быть соизмеримы с расстоянием r между их центрами.
Кулон изучал взаимодействие между зарядами, находящимися в воздухе. Дальнейшие экспериментальные исследования показали, что при прочих равных условиях сила электростатического взаимодействия между двумя точечными зарядами зависит от свойств среды, в которой эти заряды находятся, и имеет вид:
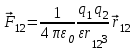 , ,
где 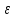 - относительная диэлектрическая проницаемость среды. - относительная диэлектрическая проницаемость среды.
Опыты Кулона не являются единственным доказательством справедливости закона обратных квадратов. В настоящее время имеется большое количество других экспериментальных данных, показывающих, что закон Кулона выполняется очень точно и притом как для очень больших, так и для очень малых расстояний. В частности, исследования атомных явлений позволяют заключить, что он справедлив, по крайней мере, вплоть до расстояний порядка 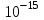 м. м.
Вопросы для самоконтроля:
1. Опишите модель точечного заряда.
2. Сформулируйте и напишите закон Кулона в системе СИ.
3. Что такое электрическая постоянная и чему она равна в СИ?
4. Как влияет диэлектрическая среда на взаимодействие помещенных в нее двух точечных зарядов?
Тема 2. Напряженность электростатического поля
Лекция № 3. Напряженность электростатического поля точечного заряда.
Цель: ввести силовую характеристику электростатического поля, изучить ее свойства и рассчитать ее для поля точечного заряда.
Основные понятия:
Напряженность – силовая характеристика электростатического поля.
Силовые линии – линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности.
Фарадей впервые высказал идею о том, что электрические заряды всегда связаны с электрическим полем, непрерывно распределенным по всему пространству, окружающему заряженные частицы или тела. Электростатическое (не зависящее от времени) поле одного заряда проявляется в его силовом действии на другой заряд, помещенный в какую-либо точку поля. Следует подчеркнуть, что поле – особый вид материи, отличный от вещества, – существует независимо от присутствия другого заряда. В свою очередь второй заряд своим полем действует на первый. Представление о полях, связанных с зарядами, лежит в основе теории близкодействия. При этом весьма важно следующее: если один из зарядов изменится (или сместится), то изменение силы, испытываемой вторым зарядом, наступит не мгновенно, а с некоторым запаздыванием, так как взаимодействие передается с конечной скоростью. В законе Кулона конечная скорость передачи взаимодействий явно не отражена.
Перейдем теперь к установлению свойств и характеристик электростатического поля.
Разделив силу, испытываемую зарядом q2, помещенным в точке А, на его значение (с учетом знака заряда), мы получим векторную характеристику поля, связанного с зарядом q1 в точке А:
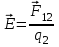 . .
Эта величина называется напряженностью электростатического поля в вакууме.
Напряженность электрического поля точечного заряда q1 в вакууме можно найти из закона Кулона:
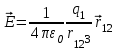 . .
Введя, для упрощения записей, обозначения 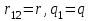 , получим , получим
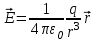 , ,
или в скалярном виде
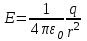 . .
Н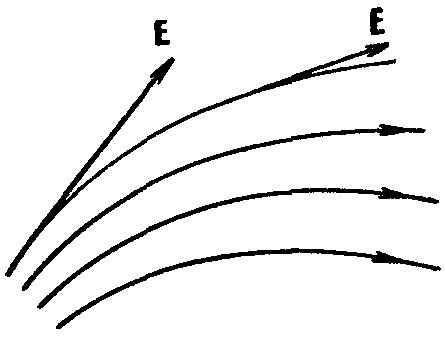 аправление вектора напряженности аправление вектора напряженности  совпадает (по определению) с направлением силы, действующей на положительный заряд. Графически электростатическое поле можно изобразить при помощи силовых линий (линий вектора напряженности). Силовыми линиями называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля. Силовые линии считаются направленными так же, как и вектор напряженности. Они нигде не пересекаются, поскольку в каждой точке поля вектор совпадает (по определению) с направлением силы, действующей на положительный заряд. Графически электростатическое поле можно изобразить при помощи силовых линий (линий вектора напряженности). Силовыми линиями называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля. Силовые линии считаются направленными так же, как и вектор напряженности. Они нигде не пересекаются, поскольку в каждой точке поля вектор  имеет лишь одно направление. Принято считать, что количество силовых линий, проведенных в некоторой области пространства, должно быть пропорционально напряженности электрического поля в этой области. имеет лишь одно направление. Принято считать, что количество силовых линий, проведенных в некоторой области пространства, должно быть пропорционально напряженности электрического поля в этой области.
И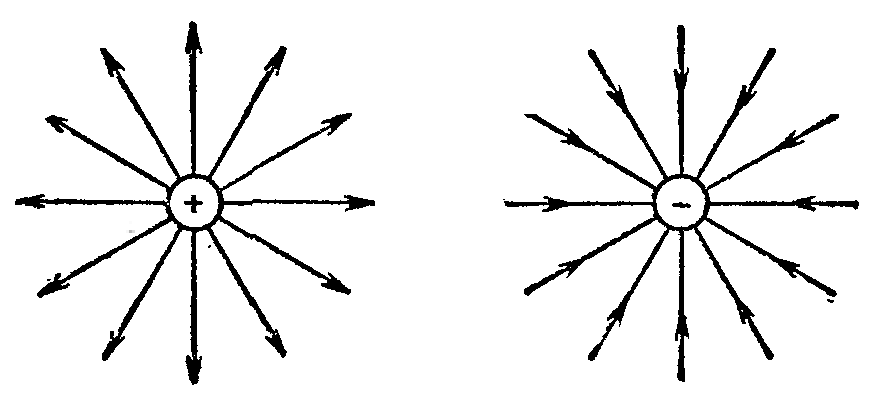 сходя из закона Кулона, силовые линии поля, создаваемого точечным зарядом, радиально направлены либо к заряду, либо от него. сходя из закона Кулона, силовые линии поля, создаваемого точечным зарядом, радиально направлены либо к заряду, либо от него.
Вопросы для самоконтроля:
1. Какие поля называются электростатическими?
2. Что такое напряженность электрического поля?
3. Чему равна напряженность поля точечного заряда?
4. Что называют электрической силовой линией?
Лекция № 4. Принцип суперпозиции полей. Напряженность поля заряженной нити, плоскости, шара.
Цель: познакомить обучающихся с двумя методами нахождения напряженности поля по известному распределению зарядов, применить их для расчета заданных распределений зарядов.
Основные понятия:
Суперпозиция полей геометрическое сложение напряженностей полей, создаваемых отдельными зарядами.
Поток вектора напряженности – величина, равная скалярному произведению вектора напряженности и ориентируемой поверхности.
Теорема Остроградского – Гаусса – интегральная формулировка закона Кулона; устанавливает связь между потоком вектора напряженности сквозь замкнутую поверхность и зарядом в объеме, ограниченном этой поверхностью.
4.1. Суперпозиция (наложение) полей.
Основной задачей электростатики является нахождение напряженности  электрического поля по известному распределению в пространстве электрических зарядов. Эта задача может быть решена на основе принципа суперпозиции электрических полей (принципа независимости действия электрических полей). электрического поля по известному распределению в пространстве электрических зарядов. Эта задача может быть решена на основе принципа суперпозиции электрических полей (принципа независимости действия электрических полей).
Р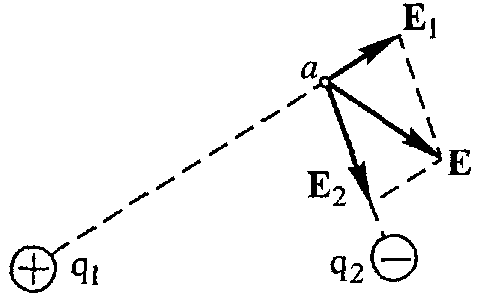 ассмотрим электрическое поле двух точечных зарядов q1 и q2. Пусть ассмотрим электрическое поле двух точечных зарядов q1 и q2. Пусть 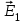 – напряженность поля в точке а, создаваемая зарядом q1 (когда заряда q2 нет вовсе), а – напряженность поля в точке а, создаваемая зарядом q1 (когда заряда q2 нет вовсе), а 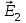 – напряженность поля заряда q2 (когда нет заряда q1). Опыт показывает, что напряженность – напряженность поля заряда q2 (когда нет заряда q1). Опыт показывает, что напряженность  результирующего поля (при наличии обоих зарядов) может быть найдена по правилу сложения векторов (по правилу параллелограмма). Или, иначе, напряженность результирующего электрического поля есть векторная сумма напряженностей полей, создаваемых отдельными зарядами. результирующего поля (при наличии обоих зарядов) может быть найдена по правилу сложения векторов (по правилу параллелограмма). Или, иначе, напряженность результирующего электрического поля есть векторная сумма напряженностей полей, создаваемых отдельными зарядами.
Правило векторного сложения электрических полей справедливо не только для двух, но и для какого угодно числа зарядов. Согласно принципу суперпозиции напряженность  электрического поля, создаваемого системой зарядов, равна геометрической сумме напряженностей электрического поля, создаваемого системой зарядов, равна геометрической сумме напряженностей 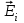 полей, создаваемых в данной точке пространства каждым из зарядов в отдельности. полей, создаваемых в данной точке пространства каждым из зарядов в отдельности.
Принцип суперпозиции электрических полей для дискретного распределения зарядов в пространстве:
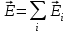 ; ;
для непрерывного распределения зарядов:
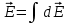 . .
Для зарядов, непрерывно распределенных в пространстве, вводят понятие плотности заряда. Если заряд q непрерывно и равномерно распределен вдоль линии длиной l, то распределение зарядов характеризуется линейной плотностью τ, которая равна заряду, приходящемуся на единицу длины
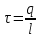 . .
Т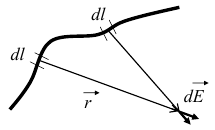 огда элементарной длине dl соответствует элементарный заряд dq = τ⋅dl, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором огда элементарной длине dl соответствует элементарный заряд dq = τ⋅dl, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 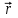 , электростатическое поле с напряженностью , электростатическое поле с напряженностью
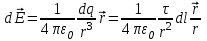 . .
Чтобы найти напряженность поля, создаваемого всеми линейно распределенными элементарными зарядами, необходимо выполнить интегрирование 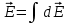 вдоль линии l распределения зарядов, учитывая направление векторов вдоль линии l распределения зарядов, учитывая направление векторов 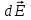 . .
Если заряд q непрерывно и равномерно распределен по поверхности площадью S, то распределение зарядов характеризуется поверхностной плотностью σ, которая равна заряду, приходящемуся на единицу площади 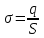 . Тогда элементарной площади ds соответствует элементарный заряд dq = σ⋅ds, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором . Тогда элементарной площади ds соответствует элементарный заряд dq = σ⋅ds, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 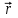 , электростатическое поле с напряженностью , электростатическое поле с напряженностью
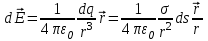 . .
Чтобы найти напряженность поля, создаваемого всеми поверхностно распределенными элементарными зарядами, необходимо выполнить интегрирование 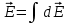 по поверхности S, вдоль которой распределены заряды, учитывая направление векторов по поверхности S, вдоль которой распределены заряды, учитывая направление векторов 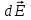 . .
Аналогично, если заряд q непрерывно и равномерно распределен в некотором объеме V, то распределение зарядов характеризуется объемной плотностью , которая равна заряду, приходящемуся на единицу объема 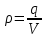 . Тогда элементарному объему dV соответствует элементарный заряд dq = ⋅dV, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором . Тогда элементарному объему dV соответствует элементарный заряд dq = ⋅dV, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 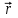 , электростатическое поле с напряженностью , электростатическое поле с напряженностью
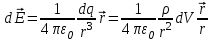 . .
Т. о., напряженность электростатического поля зависит не только от величины зарядов, создающих его, но и от их распределения в пространстве (непрерывного или дискретного).
Отметим, что справедливость этого принципа суперпозиции заранее не очевидна и в его правильности нас убеждает только опыт. А именно, вычисляя электрические поля при помощи принципа суперпозиции, мы всегда получаем результаты, согласующиеся с опытом. Однако при очень малых расстояниях ( 10-15 м) и экстремально сильных электрических полях принцип суперпозиции электрических полей, возможно, и не выполняется.
Воспользуемся принципом суперпозиции для вычисления напряженности электрического поля бесконечной заряженной с линейной плотностью τ нити.
Напряженность поля, создаваемого элементом длины нити dl, равна
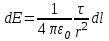 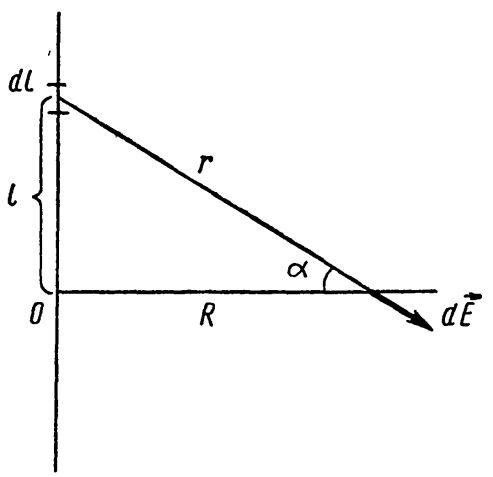 . .
Тогда, напряженность поля, создаваемая всеми линейно распределенными элементарными зарядами, найдется интегрированием вдоль бесконечной нити:
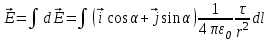 . .
Откуда
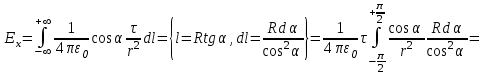
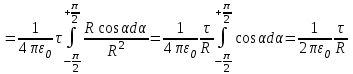 , ,
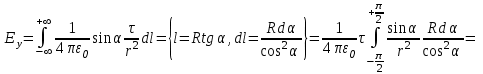
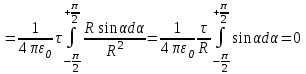 . .
Т. о., результирующая напряженность поля направлена перпендикулярно к нити и по величине равна
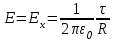 . .
4.2. Теорема Остроградского – Гаусса.
Используя принцип суперпозиции электростатических полей и закон Кулона, можно рассчитать напряженность поля любой системы зарядов в произвольной точке пространства, производя суммирование векторов напряженности полей, созданных отдельными зарядами в этой точке, но в общем случае расчет может быть достаточно сложным.
Поэтому в случае, если задача обладает пространственной симметрией, пользуются более простым методом – теоремой Остроградского – Гаусса для потока вектора напряженности.
С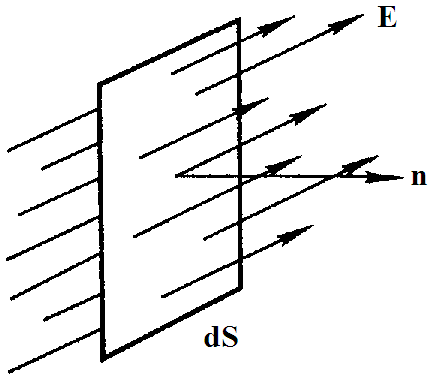 начала определим понятие потока вектора напряженности через поверхность. Рассмотрим область пространства, в которой существует электрическое поле. Поместим в некоторое место этого пространства площадку начала определим понятие потока вектора напряженности через поверхность. Рассмотрим область пространства, в которой существует электрическое поле. Поместим в некоторое место этого пространства площадку 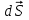 (это вектор, модуль которого равен площади dS, а направление определяется единичным вектором внешней нормали (это вектор, модуль которого равен площади dS, а направление определяется единичным вектором внешней нормали 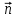 к этой поверхности). Тогда эту площадку будут пересекать силовые линии, густота которых говорит о величине поля в данной точке. Считая такую площадку практически плоской и поле в ее пределах практически постоянным, можно вычислить некоторую величину к этой поверхности). Тогда эту площадку будут пересекать силовые линии, густота которых говорит о величине поля в данной точке. Считая такую площадку практически плоской и поле в ее пределах практически постоянным, можно вычислить некоторую величину 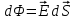 , которая называется потоком вектора напряженности электрического поля через площадку dS. , которая называется потоком вектора напряженности электрического поля через площадку dS.
Поток можно записать в виде 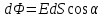 ( - угол между ( - угол между  и и 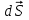 ). ).
Чтобы найти полный поток через некоторую замкнутую поверхность S, необходимо вычислить интеграл по этой поверхности:
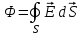 . .
Теперь сформулируем теорему Остроградского – Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на ε0:
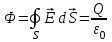 , ,
где Q – суммарный заряд, находящийся внутри замкнутой поверхности S. Если же заряд лежит во внешнем пространстве по отношению к замкнутой поверхности S, то его поток равен нулю.
4.3. Применения теоремы Остроградского – Гаусса.
Определим с помощью теоремы Остроградского – Гаусса напряженность электрического поля бесконечной заряженной с поверхностной плотностью плоскости; для определенности будем считать заряд положительным. По соображениям симметрии можно считать, что линии напряженности перпендикулярны к плоскости и направлены от нее. Рассмотрим точку А, лежащую справа от плоскости. Напряженность в этой точке направлена вправо. Если мы возьмем точку В, расположенную симметрично с точкой А влево от плоскости, то убедимся, что в ней напряженность  направлена в противоположную сторону по сравнению с направлением напряженности в точке А. Следовательно, линии напряженности будут прямыми, выходящими из плоскости и перпендикулярными к ней. направлена в противоположную сторону по сравнению с направлением напряженности в точке А. Следовательно, линии напряженности будут прямыми, выходящими из плоскости и перпендикулярными к ней.
О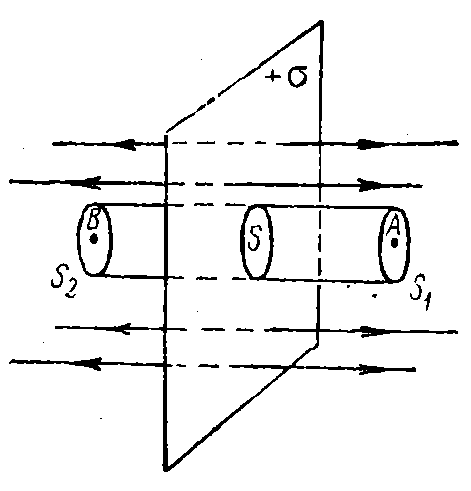 пределим величину напряженности в точке А, применяя теорему Остроградского – Гаусса. В качестве замкнутой поверхности выберем цилиндрическую поверхность, построенную следующим образом: берем произвольный участок S заряженной плоскости за среднее сечение цилиндра; боковую поверхность цилиндра проводим параллельно линиям напряженности. Оба основания цилиндра S1 и S2 проводим соответственно через точки А и В, параллельно плоскости. Тогда по соображениям симметрии можно считать, что напряженности постоянны во всех точках каждого из оснований S1 и S2, по численному значению равны друг другу и равны искомой напряженности пределим величину напряженности в точке А, применяя теорему Остроградского – Гаусса. В качестве замкнутой поверхности выберем цилиндрическую поверхность, построенную следующим образом: берем произвольный участок S заряженной плоскости за среднее сечение цилиндра; боковую поверхность цилиндра проводим параллельно линиям напряженности. Оба основания цилиндра S1 и S2 проводим соответственно через точки А и В, параллельно плоскости. Тогда по соображениям симметрии можно считать, что напряженности постоянны во всех точках каждого из оснований S1 и S2, по численному значению равны друг другу и равны искомой напряженности  в точке А. Рассчитаем поток напряженности через рассматриваемую цилиндрическую поверхность. Поток через боковую поверхность равен нулю, так как линии напряженности параллельны боковой поверхности. Следовательно, полный поток в точке А. Рассчитаем поток напряженности через рассматриваемую цилиндрическую поверхность. Поток через боковую поверхность равен нулю, так как линии напряженности параллельны боковой поверхности. Следовательно, полный поток 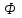 складывается из потоков 1 и 2 через основания цилиндра S1 и S2. Оба эти потока положительны. Так как поверхности S1 и S2 перпендикулярны к линиям напряженности, то потоки через них получаются умножением величины напряженности на площадь основания. Т. о., имеем: складывается из потоков 1 и 2 через основания цилиндра S1 и S2. Оба эти потока положительны. Так как поверхности S1 и S2 перпендикулярны к линиям напряженности, то потоки через них получаются умножением величины напряженности на площадь основания. Т. о., имеем:
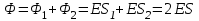 . .
По теореме Остроградского – Гаусса полный поток должен равняться полному заряду внутри этой поверхности, деленному на ε0; этот заряд равен S. Следовательно,
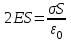
откуда искомая напряженность E получается равной
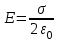 . .
Значение Е не зависит от расстояния точки А от плоскости. То же относится и к точке В. Таким образом, мы получаем справа и слева от плоскости однородные поля. Если плоскость заряжена отрицательно, то направление напряженности противоположно разобранному: линии будут входить в плоскость. Полученный результат верен только для бесконечной плоскости, так как только в таком случае могут быть использованы приведенные соображения симметрии; однако приближенно он справедлив для пространства, прилегающего к средней части конечной плоскости, вдали от ее краев.
О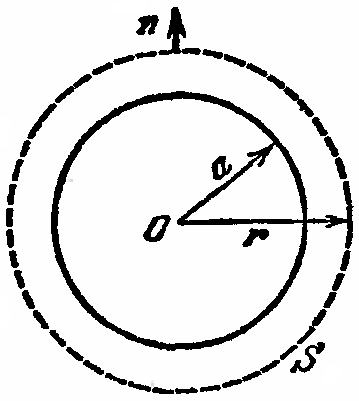 пределим, также, с помощью теоремы Остроградского – Гаусса напряженность электрического поля шара, равномерно заряженного с объемной плотностью . Ввиду шаровой симметрии вектор пределим, также, с помощью теоремы Остроградского – Гаусса напряженность электрического поля шара, равномерно заряженного с объемной плотностью . Ввиду шаровой симметрии вектор  параллелен или антипараллелен радиусу-вектору параллелен или антипараллелен радиусу-вектору 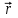 , проведенному из центра шара в точку наблюдения, а его длина Eможет зависеть только от расстояния r. Заметив это, проведем вне шара концентрическую с ним сферу S радиуса r. Поток вектора , проведенному из центра шара в точку наблюдения, а его длина Eможет зависеть только от расстояния r. Заметив это, проведем вне шара концентрическую с ним сферу S радиуса r. Поток вектора  через эту сферу через эту сферу 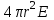 по теореме Остроградского – Гаусса равен по теореме Остроградского – Гаусса равен 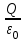 , а потому для напряженности электрического поля вне шара получаем , а потому для напряженности электрического поля вне шара получаем
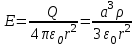 , ,
где 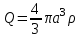 – полный заряд шара радиуса a. – полный заряд шара радиуса a.
Т. о., равномерно заряженный шар создает во внешнем пространстве такое поле, как если бы весь заряд был сосредоточен в его центре. Этот результат остается справедливым при любом сферически симметричном распределении заряда по объему шара.
Когда радиус шара пренебрежимо мал по сравнению с расстоянием r, мы получаем кулоново поле точечного заряда. Нельзя, однако, сказать, что закон Кулона является следствием теоремы Гаусса. Он получается из нее при дополнительном предположении, что поле неподвижного точечного заряда радиально и обладает шаровой симметрией.
С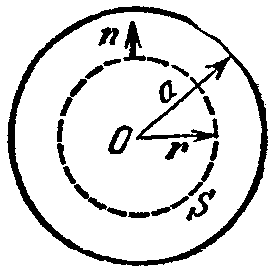 овершенно так же вычисляется поле внутри шара. Оно определяется выражением овершенно так же вычисляется поле внутри шара. Оно определяется выражением
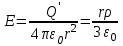 , ,
где 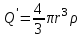 – заряд, ограниченный сферой радиуса r. – заряд, ограниченный сферой радиуса r.
Если шар равномерно заряжен с поверхностной плотностью , то напряженность электрического поля вне шара равна
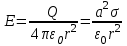 , ,
где 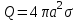 – полный заряд шара радиуса a. – полный заряд шара радиуса a.
При вычислении поля внутри шара, с учетом того, что заряд 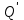 , ограниченный сферой радиуса r<aравен нулю, получим , ограниченный сферой радиуса r<aравен нулю, получим 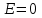 . Т. о., электрическое поле внутри шара, равномерно заряженного по поверхности, равно нулю. Данный результат остается верным и для полости произвольной формы, окруженной поверхностно заряженной оболочкой также произвольной формы. . Т. о., электрическое поле внутри шара, равномерно заряженного по поверхности, равно нулю. Данный результат остается верным и для полости произвольной формы, окруженной поверхностно заряженной оболочкой также произвольной формы.
Вопросы для самоконтроля:
1. В чем состоит принцип суперпозиции электрических полей?
2. Что называют потоком вектора напряженности через поверхность?
3. Сформулируйте теорему Остроградского – Гаусса.
4. Чему равна напряженность поля равномерно заряженных нити, плоскости и шара?
|
|
|
 Скачать 0.66 Mb.
Скачать 0.66 Mb.
 . Кулон проводил эксперименты с помощью крутильных весов. По углу закручивания упругой нити он измерял силу отталкивания одноименно заряженных шариков, а по шкале прибора – расстояние между ними. В результате этих опытов Кулон заключил, что сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, и обратно пропорциональна квадрату расстояния между зарядами:
. Кулон проводил эксперименты с помощью крутильных весов. По углу закручивания упругой нити он измерял силу отталкивания одноименно заряженных шариков, а по шкале прибора – расстояние между ними. В результате этих опытов Кулон заключил, что сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, и обратно пропорциональна квадрату расстояния между зарядами: 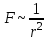 .
.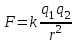
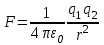 ,
,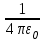 , где
, где 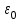 = 8,85·10-12 Кл2/(Н·м2) – электрическая постоянная.
= 8,85·10-12 Кл2/(Н·м2) – электрическая постоянная. Для того чтобы выразить не только модуль силы, но и ее направление, закон Кулона можно представить в векторной форме:
Для того чтобы выразить не только модуль силы, но и ее направление, закон Кулона можно представить в векторной форме: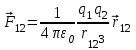 ,
,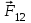 — вектор силы, действующей на заряд 1 со стороны заряда 2, а
— вектор силы, действующей на заряд 1 со стороны заряда 2, а 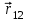 — радиус-вектор, направленный от заряда 2 к заряду 1 (рис. а и б).
— радиус-вектор, направленный от заряда 2 к заряду 1 (рис. а и б). 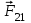 , действующая на заряд 2 со стороны заряда 1, равна
, действующая на заряд 2 со стороны заряда 1, равна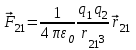 ,
,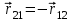 - радиус-вектор, направленный от заряда 1 к заряду 2.
- радиус-вектор, направленный от заряда 1 к заряду 2.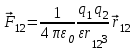 ,
,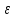 - относительная диэлектрическая проницаемость среды.
- относительная диэлектрическая проницаемость среды.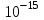 м.
м.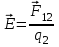 .
.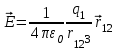 .
.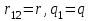 , получим
, получим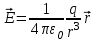 ,
, 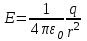 .
. аправление вектора напряженности
аправление вектора напряженности  совпадает (по определению) с направлением силы, действующей на положительный заряд. Графически электростатическое поле можно изобразить при помощи силовых линий (линий вектора напряженности). Силовыми линиями называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля. Силовые линии считаются направленными так же, как и вектор напряженности. Они нигде не пересекаются, поскольку в каждой точке поля вектор
совпадает (по определению) с направлением силы, действующей на положительный заряд. Графически электростатическое поле можно изобразить при помощи силовых линий (линий вектора напряженности). Силовыми линиями называют линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля. Силовые линии считаются направленными так же, как и вектор напряженности. Они нигде не пересекаются, поскольку в каждой точке поля вектор  сходя из закона Кулона, силовые линии поля, создаваемого точечным зарядом, радиально направлены либо к заряду, либо от него.
сходя из закона Кулона, силовые линии поля, создаваемого точечным зарядом, радиально направлены либо к заряду, либо от него. ассмотрим электрическое поле двух точечных зарядов q1 и q2. Пусть
ассмотрим электрическое поле двух точечных зарядов q1 и q2. Пусть 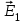 – напряженность поля в точке а, создаваемая зарядом q1 (когда заряда q2 нет вовсе), а
– напряженность поля в точке а, создаваемая зарядом q1 (когда заряда q2 нет вовсе), а 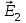 – напряженность поля заряда q2 (когда нет заряда q1). Опыт показывает, что напряженность
– напряженность поля заряда q2 (когда нет заряда q1). Опыт показывает, что напряженность 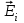 полей, создаваемых в данной точке пространства каждым из зарядов в отдельности.
полей, создаваемых в данной точке пространства каждым из зарядов в отдельности.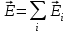 ;
;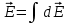 .
.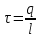 .
. огда элементарной длине dl соответствует элементарный заряд dq = τ⋅dl, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором
огда элементарной длине dl соответствует элементарный заряд dq = τ⋅dl, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 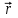 , электростатическое поле с напряженностью
, электростатическое поле с напряженностью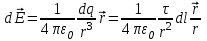 .
.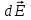 .
.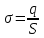 . Тогда элементарной площади ds соответствует элементарный заряд dq = σ⋅ds, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором
. Тогда элементарной площади ds соответствует элементарный заряд dq = σ⋅ds, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 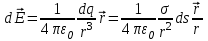 .
.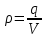 . Тогда элементарному объему dV соответствует элементарный заряд dq = ⋅dV, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором
. Тогда элементарному объему dV соответствует элементарный заряд dq = ⋅dV, который считается точечным. Этот элементарный заряд dq создает в некоторой точке пространства, описываемой радиус-вектором 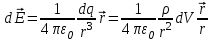 .
.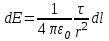
 .
.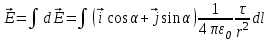 .
.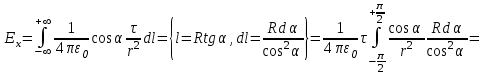
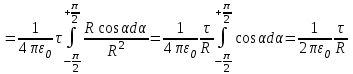 ,
,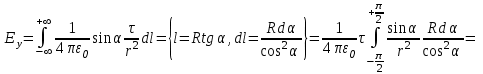
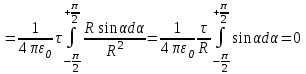 .
.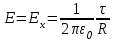 .
. начала определим понятие потока вектора напряженности через поверхность. Рассмотрим область пространства, в которой существует электрическое поле. Поместим в некоторое место этого пространства площадку
начала определим понятие потока вектора напряженности через поверхность. Рассмотрим область пространства, в которой существует электрическое поле. Поместим в некоторое место этого пространства площадку 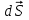 (это вектор, модуль которого равен площади dS, а направление определяется единичным вектором внешней нормали
(это вектор, модуль которого равен площади dS, а направление определяется единичным вектором внешней нормали 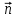 к этой поверхности). Тогда эту площадку будут пересекать силовые линии, густота которых говорит о величине поля в данной точке. Считая такую площадку практически плоской и поле в ее пределах практически постоянным, можно вычислить некоторую величину
к этой поверхности). Тогда эту площадку будут пересекать силовые линии, густота которых говорит о величине поля в данной точке. Считая такую площадку практически плоской и поле в ее пределах практически постоянным, можно вычислить некоторую величину 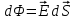 , которая называется потоком вектора напряженности электрического поля через площадку dS.
, которая называется потоком вектора напряженности электрического поля через площадку dS. 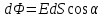 ( - угол между
( - угол между 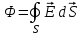 .
.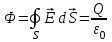 ,
, пределим величину напряженности в точке А, применяя теорему Остроградского – Гаусса. В качестве замкнутой поверхности выберем цилиндрическую поверхность, построенную следующим образом: берем произвольный участок S заряженной плоскости за среднее сечение цилиндра; боковую поверхность цилиндра проводим параллельно линиям напряженности. Оба основания цилиндра S1 и S2 проводим соответственно через точки А и В, параллельно плоскости. Тогда по соображениям симметрии можно считать, что напряженности постоянны во всех точках каждого из оснований S1 и S2, по численному значению равны друг другу и равны искомой напряженности
пределим величину напряженности в точке А, применяя теорему Остроградского – Гаусса. В качестве замкнутой поверхности выберем цилиндрическую поверхность, построенную следующим образом: берем произвольный участок S заряженной плоскости за среднее сечение цилиндра; боковую поверхность цилиндра проводим параллельно линиям напряженности. Оба основания цилиндра S1 и S2 проводим соответственно через точки А и В, параллельно плоскости. Тогда по соображениям симметрии можно считать, что напряженности постоянны во всех точках каждого из оснований S1 и S2, по численному значению равны друг другу и равны искомой напряженности 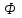 складывается из потоков 1 и 2 через основания цилиндра S1 и S2. Оба эти потока положительны. Так как поверхности S1 и S2 перпендикулярны к линиям напряженности, то потоки через них получаются умножением величины напряженности на площадь основания. Т. о., имеем:
складывается из потоков 1 и 2 через основания цилиндра S1 и S2. Оба эти потока положительны. Так как поверхности S1 и S2 перпендикулярны к линиям напряженности, то потоки через них получаются умножением величины напряженности на площадь основания. Т. о., имеем: 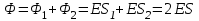 .
. 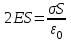
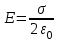 .
.  пределим, также, с помощью теоремы Остроградского – Гаусса напряженность электрического поля шара, равномерно заряженного с объемной плотностью . Ввиду шаровой симметрии вектор
пределим, также, с помощью теоремы Остроградского – Гаусса напряженность электрического поля шара, равномерно заряженного с объемной плотностью . Ввиду шаровой симметрии вектор 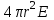 по теореме Остроградского – Гаусса равен
по теореме Остроградского – Гаусса равен 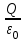 , а потому для напряженности электрического поля вне шара получаем
, а потому для напряженности электрического поля вне шара получаем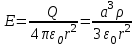 ,
,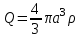 – полный заряд шара радиуса a.
– полный заряд шара радиуса a. овершенно так же вычисляется поле внутри шара. Оно определяется выражением
овершенно так же вычисляется поле внутри шара. Оно определяется выражением 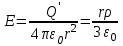 ,
,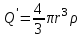 – заряд, ограниченный сферой радиуса r.
– заряд, ограниченный сферой радиуса r.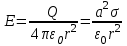 ,
,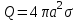 – полный заряд шара радиуса a.
– полный заряд шара радиуса a.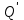 , ограниченный сферой радиуса r<aравен нулю, получим
, ограниченный сферой радиуса r<aравен нулю, получим 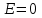 . Т. о., электрическое поле внутри шара, равномерно заряженного по поверхности, равно нулю. Данный результат остается верным и для полости произвольной формы, окруженной поверхностно заряженной оболочкой также произвольной формы.
. Т. о., электрическое поле внутри шара, равномерно заряженного по поверхности, равно нулю. Данный результат остается верным и для полости произвольной формы, окруженной поверхностно заряженной оболочкой также произвольной формы.