конспект. КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальносте. Конспект лекций по физике для студентов 12 курсов специальностей технического профиля спо раздел Электростатика Ейск, 2017
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Тема 3. Потенциальность электростатического поля Лекция № 5. Работа сил электростатического поля. Цель: сформулировать критерии потенциальности поля, доказать потенциальность электростатического поля. Основные понятия: Потенциальное поле силовое поле, в котором работа сил поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек. Циркуляция вектора напряженности – интеграл по замкнутому контуру 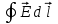 . .5.1. Потенциальность электростатического поля. Н 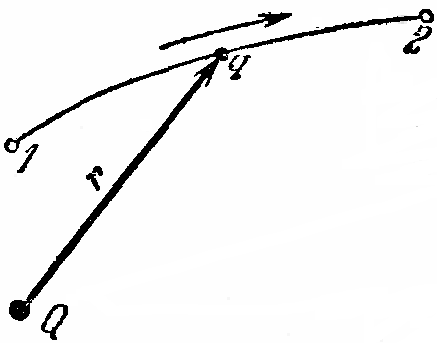 еподвижный точечный заряд Q возбуждает в вакууме электрическое поле еподвижный точечный заряд Q возбуждает в вакууме электрическое поле 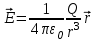 . Пусть в этом поле перемещается другой точечный заряд q, переходя из начального положения 1 в конечное положение 2 вдоль произвольной кривой 12. Работа, совершаемая силами поля при таком перемещении, выражается интегралом . Пусть в этом поле перемещается другой точечный заряд q, переходя из начального положения 1 в конечное положение 2 вдоль произвольной кривой 12. Работа, совершаемая силами поля при таком перемещении, выражается интегралом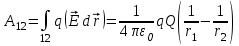 . .Т. о., при любом выборе начальной и конечной точек 1 и 2 работа 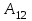 не зависит от формы пути, а определяется только положениями этих точек. Силовые поля, удовлетворяющие такому условию, называются потенциальными или консервативными. Следовательно, электростатическое поле точечного заряда есть поле потенциальное. не зависит от формы пути, а определяется только положениями этих точек. Силовые поля, удовлетворяющие такому условию, называются потенциальными или консервативными. Следовательно, электростатическое поле точечного заряда есть поле потенциальное.Доказанное справедливо для электрического поля любой системы неподвижных точечных зарядов. В общем случае любую систему зарядов можно мысленно разделить на достаточно малые части, каждая из которых может рассматриваться как точечный заряд. В число таких зарядов должны быть включены и индукционные заряды на проводниках и диэлектриках. Поэтому всякое электростатическое поле, независимо от того, создается оно в вакууме или в веществе, является полем потенциальным. Допустим, что в электростатическом поле заряд переносится из точки 1 в точку 2 сначала по пути 132, а затем по пути 142. В обоих случаях работы сил поля одинаковы: 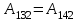 . Если заряд переносится по замкнутому пути 13241, то на участке 241 работа изменит знак: . Если заряд переносится по замкнутому пути 13241, то на участке 241 работа изменит знак: 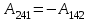 , а потому , а потому 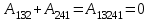 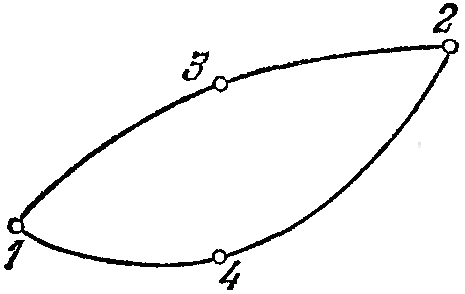 . Значит, при перемещении заряда по любому замкнутому пути работа в электростатическом поле равна нулю. Если перемещаемый заряд единичный, то работа сводится к криволинейному интегралу . Значит, при перемещении заряда по любому замкнутому пути работа в электростатическом поле равна нулю. Если перемещаемый заряд единичный, то работа сводится к криволинейному интегралу 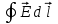 . Такой интеграл называется циркуляцией вектора . Такой интеграл называется циркуляцией вектора  по соответствующему замкнутому контуру. Т. о., для любого замкнутого контура по соответствующему замкнутому контуру. Т. о., для любого замкнутого контура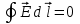 . .Это приводит к другому определению потенциальности поля, эквивалентному данному выше. Векторное поле  называется потенциальным, если циркуляция вектора называется потенциальным, если циркуляция вектора  по любому замкнутому контуру равна нулю. по любому замкнутому контуру равна нулю.Из последнего уравнения следует, что силовые линии электростатического поля не могут быть замкнутыми. Для доказательства допустим противное. Пусть силовая линия замкнута. Возьмем ее в качестве контура интегрирования С. При обходе этого контура в положительном направлении силовой линии подынтегральное выражение в интеграле 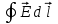 , а с ним и самый интеграл существенно положительны. Это противоречит последнему уравнению, что и доказывает наше утверждение. , а с ним и самый интеграл существенно положительны. Это противоречит последнему уравнению, что и доказывает наше утверждение.Вопросы для самоконтроля. 1. Каково условие потенциальности силового поля. Докажите, что электростатическое поле является потенциальным. 2. Что называют циркуляцией вектора напряженности по замкнутому контуру? 3. Приведите критерий потенциальности поля в терминах циркуляции вектора напряженности? 4. Каково свойство силовых линий электростатического поля? Лекция № 6. Потенциал электростатического поля. Цель: дать понятие потенциала электростатического поля, рассмотреть его свойства и методы вычисления. Основные понятия: Потенциал – энергетическая характеристика электростатического поля; равен работе, которую необходимо затратить для перемещения положительного заряда из бесконечности в данную точку. Градиент скалярной функции – это вектор, направленный в сторону максимального возрастания этой функции. Эквипотенциальная поверхность – это поверхность, на которой потенциал остается постоянным. Нормировка потенциала – выбор точки с нулевым потенциалом. 6.1. Понятие потенциала электростатического поля. Для потенциальных полей (полей, созданных исключительно зарядами, но не вихрями) можно ввести понятие потенциала или, точнее, разности потенциалов. Разностью потенциалов 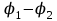 между точками 1 и 2 называется работа, совершаемая силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2. Такое определение имеет смысл потому, что эта работа не зависит от формы пути, а определяется только положениями начальной и конечной точек его. Потенциалу какой-либо произвольной точки поля О можно условно приписать любое значение между точками 1 и 2 называется работа, совершаемая силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2. Такое определение имеет смысл потому, что эта работа не зависит от формы пути, а определяется только положениями начальной и конечной точек его. Потенциалу какой-либо произвольной точки поля О можно условно приписать любое значение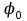 . Тогда потенциалы всех прочих точек поля определятся однозначно. Если изменить значение . Тогда потенциалы всех прочих точек поля определятся однозначно. Если изменить значение 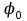 , то потенциалы в точке О и во всех других точках изменятся на одну и ту же постоянную. Т. о., потенциал определен с точностью до аддитивной постоянной. Значение этой постоянной не играет роли, так как физические явления зависят только от напряженностей электрических полей. Электрические же поля связаны не с абсолютными значениями потенциалов, а с их разностями между различными точками пространства. От значения аддитивной постоянной эти поля не зависят. В теоретической физике за нулевой потенциал удобно принимать потенциал бесконечно удаленной точки пространства. Тогда потенциал можно определить как работу, которую необходимо затратить для перемещения единичного положительного заряда из бесконечности в данную точку. На практике за нулевой потенциал обычно принимают потенциал Земли. В этом случае потенциалом любой точки электростатического поля называется величина, численно равная работе, которую необходимо затратить, чтобы перенести единичный положительный заряд с поверхности Земли в данную точку поля. , то потенциалы в точке О и во всех других точках изменятся на одну и ту же постоянную. Т. о., потенциал определен с точностью до аддитивной постоянной. Значение этой постоянной не играет роли, так как физические явления зависят только от напряженностей электрических полей. Электрические же поля связаны не с абсолютными значениями потенциалов, а с их разностями между различными точками пространства. От значения аддитивной постоянной эти поля не зависят. В теоретической физике за нулевой потенциал удобно принимать потенциал бесконечно удаленной точки пространства. Тогда потенциал можно определить как работу, которую необходимо затратить для перемещения единичного положительного заряда из бесконечности в данную точку. На практике за нулевой потенциал обычно принимают потенциал Земли. В этом случае потенциалом любой точки электростатического поля называется величина, численно равная работе, которую необходимо затратить, чтобы перенести единичный положительный заряд с поверхности Земли в данную точку поля.Работа сил поля при перемещении заряда q0 по произвольному пути из начальной точки 1 в конечную точку 2 определятся выражением 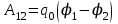 . .Практической единицей потенциала является вольт. Вольт есть разность потенциалов между такими точками, когда при перемещении одного кулона электричества из одной точки в другую электрическое поле совершает работу в один джоуль: 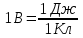 . .Найдем связь потенциала с напряженностью электрического поля. Пусть 1 и 2 – бесконечно близкие точки, расположенные на оси X, так что 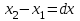 . Работа при перемещении единицы заряда из точки 1 в точку 2 будет . Работа при перемещении единицы заряда из точки 1 в точку 2 будет 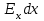 . Та же работа равна . Та же работа равна 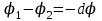 . Приравнивая оба выражения, получим . Приравнивая оба выражения, получим 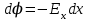 . . Аналогичное рассуждение применимо для осей Y и Z. В результате получаются три соотношения: 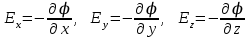 . .Их можно объединить в одну векторную формулу: 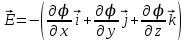 . .Так как  есть вектор, то и выражение, стоящее в скобках, есть также вектор. Он называется градиентом скаляра есть вектор, то и выражение, стоящее в скобках, есть также вектор. Он называется градиентом скаляра 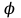 и обозначается и обозначается 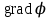 . Таким образом, по определению . Таким образом, по определению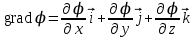 . .Теперь можно записать: 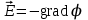 . .Из данной формулы следует, что одной величиной (потенциал – величина скалярная и в каждой точке имеет одно определенное значение) мы определяем три величины (напряженность – величина векторная и в каждой точке задается тремя проекциями на оси координат Ex, Ey, Ez). Но, все дело в том, что в потенциальном поле проекции Ex, Ey, Ez не являются независимыми величинами, а связаны между собой. Эта связь следует из условия потенциальности, согласно которому работа поля на замкнутом пути равна нулю. Д 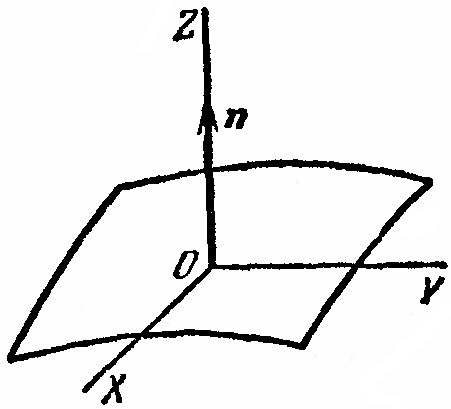 ля выяснения геометрического смысла градиента введем понятие эквипотенциальных поверхностей, или поверхностей равного потенциала. Как показывает само название, эквипотенциальная поверхность есть такая поверхность, на которой потенциал остается постоянным. Он может меняться только при переходе от одной эквипотенциальной поверхности к другой. Возьмем на эквипотенциальной поверхности произвольную точку О и введем локальную систему координат с началом в этой точке. Ось Z направим по нормали ля выяснения геометрического смысла градиента введем понятие эквипотенциальных поверхностей, или поверхностей равного потенциала. Как показывает само название, эквипотенциальная поверхность есть такая поверхность, на которой потенциал остается постоянным. Он может меняться только при переходе от одной эквипотенциальной поверхности к другой. Возьмем на эквипотенциальной поверхности произвольную точку О и введем локальную систему координат с началом в этой точке. Ось Z направим по нормали 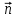 к эквипотенциальной поверхности в сторону возрастания потенциала к эквипотенциальной поверхности в сторону возрастания потенциала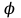 . Можно показать, что тогда . Можно показать, что тогда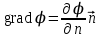 . .То есть, функция 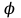 возрастает наиболее быстро в направлении нормали возрастает наиболее быстро в направлении нормали 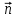 . Поэтому можно дать следующее определение. Градиент функции . Поэтому можно дать следующее определение. Градиент функции 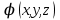 есть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функции есть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функции 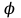 в том же направлении. Преимущество этого определения состоит в том, что оно носит инвариантный характер, т. е. никак не связано с выбором какой бы то ни было системы координат. в том же направлении. Преимущество этого определения состоит в том, что оно носит инвариантный характер, т. е. никак не связано с выбором какой бы то ни было системы координат.Вектор  направлен противоположно вектору градиента потенциала направлен противоположно вектору градиента потенциала 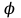 . Электрические силовые линии являются, таким образом, линиями, вдоль которых потенциал . Электрические силовые линии являются, таким образом, линиями, вдоль которых потенциал 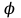 изменяется наиболее быстро. Они нормальны к эквипотенциальным поверхностям. Эквипотенциальные поверхности могут служить поэтому для наглядного изображения картины поля. Обычно их чертят так, что при переходе от одной эквипотенциальной поверхности к соседней потенциал получает одно и то же приращение изменяется наиболее быстро. Они нормальны к эквипотенциальным поверхностям. Эквипотенциальные поверхности могут служить поэтому для наглядного изображения картины поля. Обычно их чертят так, что при переходе от одной эквипотенциальной поверхности к соседней потенциал получает одно и то же приращение 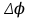 . Чем меньше выбрано . Чем меньше выбрано 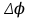 , тем детальнее будет представлено распределение потенциала в пространстве, а с ним и картина электростатического поля. Для большей наглядности чертят также силовые линии, ортогональные к семейству поверхностей равного потенциала. Там, где (при постоянном , тем детальнее будет представлено распределение потенциала в пространстве, а с ним и картина электростатического поля. Для большей наглядности чертят также силовые линии, ортогональные к семейству поверхностей равного потенциала. Там, где (при постоянном 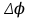 ) соседние эквипотенциальные поверхности наиболее близко подходят друг к другу, напряженность электрического поля максимальна. Наоборот, в местах, где расстояния между ними велики, будет мала и напряженность поля ) соседние эквипотенциальные поверхности наиболее близко подходят друг к другу, напряженность электрического поля максимальна. Наоборот, в местах, где расстояния между ними велики, будет мала и напряженность поля  . Поверхность проводника есть одна из эквипотенциальных поверхностей, и силовые линии должны подходить к ней нормально. Внутри проводника . Поверхность проводника есть одна из эквипотенциальных поверхностей, и силовые линии должны подходить к ней нормально. Внутри проводника 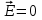 , а потому потенциал , а потому потенциал 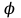 должен иметь одно и то же значение во всех точках проводника. Здесь эквипотенциальная поверхность вырождается в эквипотенциальный объем. должен иметь одно и то же значение во всех точках проводника. Здесь эквипотенциальная поверхность вырождается в эквипотенциальный объем.6.2. Вычисление потенциала по напряженности поля. Если известен потенциал 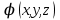 , то напряженность электрического поля можно вычислить его дифференцированием по координатам , то напряженность электрического поля можно вычислить его дифференцированием по координатам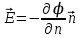 . . Обратная задача вычисления потенциала по напряженности поля решается интегрированием 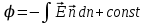 . . Рассмотрим простейшие примеры на вычисление потенциала. Вычислим потенциал электрического поля точечного заряда q. Напряженность электрического поля точечного заряда 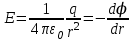 . .Откуда 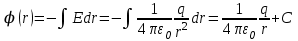 . .Для нахождения значения постоянной Cвоспользуемся условием нормировки потенциала на бесконечности: 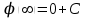 , , откуда C=0. Окончательно получаем 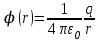 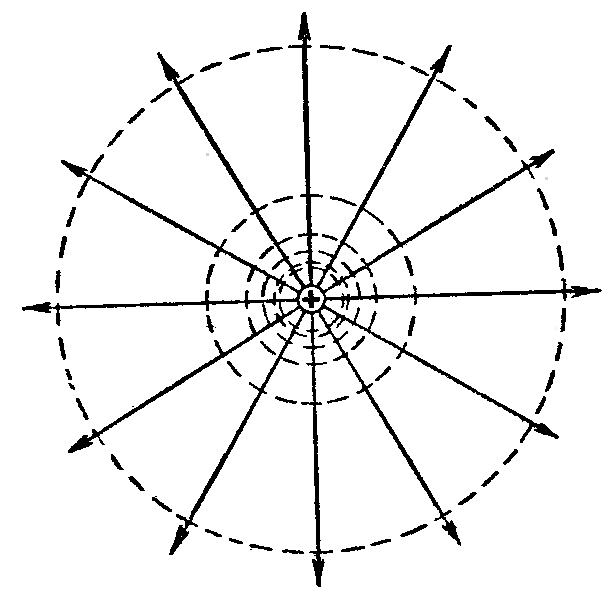 . .Потенциал может быть положительным или отрицательным, в зависимости от знака заряда, который его создает. На рисунке показаны эквипотенциальные поверхности и линии напряженности для поля точечного заряда. В соответствии с характером изменения  эквипотенциальные поверхности при приближении к заряду становятся гуще. эквипотенциальные поверхности при приближении к заряду становятся гуще.Если нас интересует потенциал, созданный системой точечных зарядов, то нужно просто сложить потенциалы, создаваемые в данной точке отдельными зарядами 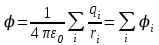 , ,где i – номер заряда, ri – его расстояние до заданной точки. Данная формула является следствием суперпозиции полей. Но напряженности, создаваемые отдельными зарядами, складываются как векторы, а потенциалы – величины скалярные, поэтому сложение их выполняется более просто. Потенциал, созданный системой непрерывно распределенных зарядов, находится интегрированием (по длине, поверхности или объему, в зависимости от вида распределения зарядов) 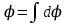 , ,где 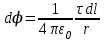 (для линейно распределенного с плотностью τ вдоль длины l заряда), (для линейно распределенного с плотностью τ вдоль длины l заряда), 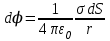 (для поверхностно распределенного с плотностью вдоль площади S заряда), (для поверхностно распределенного с плотностью вдоль площади S заряда), 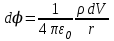 (для объемно распределенного с плотностью вдоль объема V заряда). (для объемно распределенного с плотностью вдоль объема V заряда).В 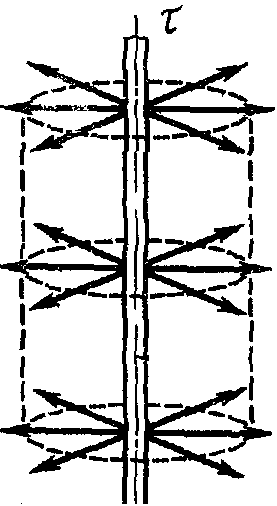 ычислим потенциал электрического поля бесконечной заряженной с линейной плотностью τ нити. Напряженность электрического поля такой нити ычислим потенциал электрического поля бесконечной заряженной с линейной плотностью τ нити. Напряженность электрического поля такой нити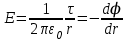 . . Откуда 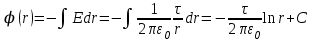 . .Здесь нельзя считать потенциал бесконечно удаленных точек равным нулю, так как сама нить считается бесконечно длинной. Поэтому постоянная остается C неопределенной; но это не создает практических неудобств, потому что важно знать лишь разность потенциалов. На рисунке показаны эквипотенциальные поверхности и линии напряженности для поля бесконечной заряженной нити. В 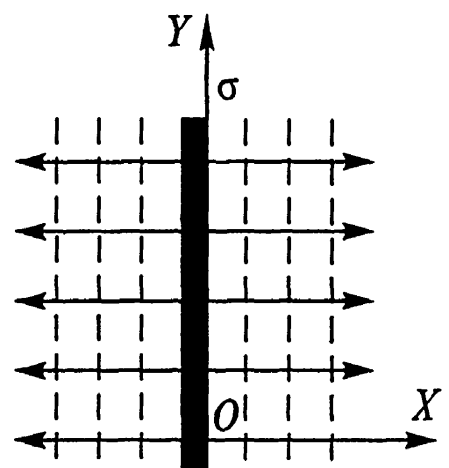 ычислим потенциал электрического поля бесконечной заряженной с поверхностной плотностью плоскости. Начало координат поместим на заряженной плоскости, ось X направим перпендикулярно к ней. Напряженность электрического поля такой плоскости ычислим потенциал электрического поля бесконечной заряженной с поверхностной плотностью плоскости. Начало координат поместим на заряженной плоскости, ось X направим перпендикулярно к ней. Напряженность электрического поля такой плоскости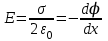 . .Откуда 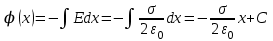 . .С учетом того, что потенциал должен уменьшаться при росте  , получим , получим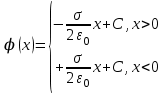 . .Постоянная С одна и та же в обоих выражениях, так как при переходе через заряженную плоскость потенциал должен изменяться непрерывно. Никаким выбором постоянной С нельзя добиться обращения потенциала в нуль в бесконечности. Это связано с тем, что в рассматриваемом случае в бесконечности имеются не только поля, но и сами заряды. Для плоскости конечных размеров полученными выражениями можно пользоваться только при таких х, которые малы по сравнению с размерами плоскости. При х порядка размеров плоскости выражение для становится очень сложным. На очень больших расстояниях плоскость ведет себя как точечный заряд. Разумеется, для конечной плоскости постоянную С в полученных формулах всегда можно выбрать так, чтобы в бесконечности потенциал обратился в нуль. Однако для вычисления С надо знать выражение для потенциала не только вблизи плоскости, но и на любых расстояниях от нее. На рисунке показаны эквипотенциальные поверхности и линии напряженности для поля бесконечной заряженной плоскости. В заключение еще раз отметим, что условию нормировки нельзя удовлетворить лишь в тех случаях, когда рассматривается абстрактное поле, создаваемое бесконечно протяженными заряженными телами (бесконечная нить, бесконечные плоскости и пр.). Вопросы для самоконтроля. 1. Дайте определение потенциала электростатического поля. 2. Что принимают за нулевой потенциал в теоретической физике и на практике? 3. Как связана работа перемещения заряда в электростатическом поле с напряженностью и потенциалом поля. 4. Как называется единица измерения потенциала? 5. Что называют эквипотенциальной поверхностью? 6. Какова связь между потенциалом и напряженностью электростатического поля? |
