3.Конспекты лекций Н. Конспекты лекций по дисциплине Теория и методика формирования элементарных математических представлений у детей дошкольного возраста
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
Методика знакомства со свойствами геометрических фигур
- Как называется? - Провокационный (показываем новую фигуру (овал) и спрашиваем: «Это круг?») - Чем похожи? - Чем отличаются?
- фигуры отличаются только по форме, - фигуры разного цвета, размеров, пропорций.
- Нахождение фигуры по образцу («Найди свой домик», «Чей домик быстрее соберется», «Автомобили и гаражи»). - Нахождение фигуры по названию («Чудесный мешочек», «Дай мне названную фигуру»). - Нахождение фигуры по описанию (перечисление характерных свойств), «Отгадай». - Составление фигур из частей (игры-головоломки: «Пифагор», «Танграмм», «Калумбово яйцо», активно используются в программе «Детство»).
Виды заданий 1. Построить треугольник, квадрат, прямоугольник. После формулировки задания анализируем фигуры и выясняем, сколько сторон, углов, равны ли стороны, сколько надо взять палочек. Если у детей возникают сложности, то дается индивидуальный образец. 2. Провокационное задание: выложить круг из палочек (нельзя - у круга нет сторон). 3. Задание занимательного характера на смекалку: выложить два треугольника из 5-ти палочек. На 2-ом этапе (старшая группа). Кроме палочек одинаковой длины предлагаем палочки разной длины: - построй фигуры разные по величине; - построй треугольники с разными по длине сторонами; - построй трапецию, ромб. Предварительно детям задаются вопросы (как на первом этапе). Задания на смекалку. - как получить из прямоугольника трапецию. Предложить одну палочку, чтобы получилась другая фигура. - можно предложить выложить домик, кораблик и т.д.
- Накрываем прямой ладошкой фигуру на столе. Если ладошка касается стола – фигура плоская, если нет - объемная. Или: если фигура прячется в ладошках, то она плоская, если нет - объемная. Плоские фигуры – это «письма», а объемные «посылки», не помещающиеся в почтовую прорезь. - Применяется подсчет углов (например, у квадрата – 4, а у куба – 8). - Плоские фигуры можно изобразить на листе бумаги в процессе рисования или аппликации, а объемные – в процессе лепки или конструирования из бумаги или строительных деталей. Если надо нарисовать объемный предмет, то его изображаем в виде соответствующей плоской фигуры. Замечания о прямоугольнике. 1. Вначале отличие прямоугольника и квадрата показывается путем наложения. У квадрата выступают кусочки, значит фигуры разные. 2. У квадрата все стороны равны, а у простого прямоугольника соседние стороны не равны. Проверяем это одним из следующих приёмов: - сгибание листа до совмещения соседних сторон; - использование условной мерки. Важно, чтобы дети понимали, что квадрат является прямоугольником. Можно сказать, что квадрат - волшебный прямоугольник (все стороны равны). В старшей группе проводится обобщение понятия «прямоугольник», предварительно поясняется понятие «прямой угол». Сначала уточнятся, что такое угол.   Показываем и называем, что этот кусочек плоскости – угол (часть плоскости между сторонами, имеющими общую точу). Для того чтобы дать представление о прямом угле, рассматривается 2 картинки:  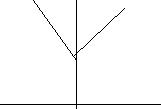  1  . Дерево растет ровно, прямо, значит между деревом и землей прямой угол. . Дерево растет ровно, прямо, значит между деревом и землей прямой угол.2. Подул ветер, и дерево наклонилось. Дерево стоит не прямо, значит угол не прямой. Далее рассматриваются различные фигуры, сравниваются и измеряются у них углы с помощью условной мерки. равной по величине прямому углу. Чтобы дети не путали угол с треугольником, край условной мерки должен быть не прямой линией.  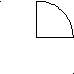 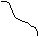  Проводятся упражнения по прикладыванию мерки к углам разных фигур. Поясняется происхождение слова «прямоугольник»: «прямой» + «угол». Упражнение: измерить углы у предметов в групповой комнате с помощью условной мерки. Замечания об овале. Более точный способ показа отличия овала от круга - это измерение осей. Пояснение понятия «ось»: «У круга и овала сторон нет, мы нарисуем линию внутри фигур через середину фигуры от одного края к другому. Эти линии называются «оси». Приводятся примеры округлых предметов, в которых имеется ось, подводя к выводу: у круга – все оси равны между собой, а у овала – нет. Два способа измерение осей: - с помощью условной мерки. - сгибание по оси. Замечания о ромбе. В старш.возр. показывается сначала сходство между ромбом и квадратом (4 угла; 4 стороны, все стороны равны). Отличие заключается в том, что у ромба не все углы равны. Это показывается при помощи условной мерки, равной прямому углу. Знакомство с ромбом происходит в процессе аппликации и рисования. Замечания о трапеции. В старш.возр. при сравнении трапеции с прямоугольником выделяются следующие отличия: 1) у трапеции не все углы прямые. 2) параллельные противоположные стороны у трапеции не равны (проверяется путем сгибания до совмещения противоположных сторон, либо путем измерения условной меркой). 3) У трапеции 2 стороны наклонные (не параллельные). Детям поясняется параллельность через показ того, что расстояние между сторонами прямоугольника одинаково, а между сторонами трапеции нет. Приводим примеры параллельности: электропровода, рельсы, предметы мебели. Затем трапеция сравнивается с треугольником (крыша бывает разной формы). Отличия: у треугольника 3 угла и 3 стороны, а у трапеции 4 угла и 4 стороны. На занятиях по аппликации показываются способы получения трапеции сначала из прямоугольника, а затем из треугольника. Замечания о цилиндре. В среднем возр. цилиндр сравнивается с шаром и кубом. Сначала показывается, чем похож и чем отличается цилиндр от шара, а затем - от куба. Цилиндр для сравнения с шаром кладется на бок и выделяются сходства фигур: 1) боковая поверхность обеих фигур не имеет препятствий. 2) шар и цилиндр катятся. 3) если положить шар на шар и цилиндр на цилиндр, то башенка не получается. Затем цилиндр переворачивается на основание, так он на шар не похож (есть препятствие, не катится, башенку из цилиндров можно построить). Обращается внимание, что в таком положении он похож на куб. Делается вывод: цилиндр – хитрая фигура, если лежит на боку - похожа на шар, если стоит на основании, то - на куб. В старшем возрасте цилиндр сравнивается с овалоидом в процессе лепки. Сначала выясняется, чем похожи эти фигуры. Затем показывается единственное отличие: если цилиндр стоит на основании, то он устойчив, а овалоид неустойчив в любом положении. Существуют также отличия в приемах лепки. Замечания о конусе. Отличия конуса от цилиндра: 1) из цилиндров можно построить башенку; а из конусов – нельзя; 2) цилиндр катится вперед – назад, конус – по кругу; 3) у цилиндра и пол, и потолок имеют форму круга; 4) толщина цилиндра внизу и вверху одинаковая, конус внизу толстый, а вверху тоненький. В старш. возр. с конусом сравниваем пирамиду и треугольную призму. Отличие пирамиды от конуса: 1) у пирамиды ребристая боковая поверхность. 2) основание у конуса – круг, у пирамиды – многоугольник. Отличие конуса и треугольной призмы: 1) поверхность у призмы негладкая, ребристая, 2) призма не катится, 3) у треугольной призмы 2 острые вершины, когда лежит на боку. 4) у треугольной призмы основание другой формы, 5) разное количество вершин. Схожесть: обе фигуры используются как крыша. Замечания о призме. Знакомство с призмой происходит в старшем возрасте на основе сравнения с кубом (аналогично как сравнивались прямоугольник с квадратом). Отличия: все стороны куба (ребра) равны, а у призмы общего вида соседние стороны не равны (измеряются условной меркой). К концу ст. возраста показываются отличия 4-угольной и 3-угольной призм. 1) основания у 4-угольной призмы имеет форму четырехугольника, а у треугольной призмы – треугольника. Поэтому они по-разному называются. 2) 4-угольная призма устойчива (можно построить башенку), если лежит на боковой грани, а 3-угольная – нет. Эта фигура используется как крыша в конструировании. Замечания об овалоиде. Отличия овалоида и шара – отличительные приемы в лепке фигур: шар – раскатывание круговыми движениями, овалоид только вперед - назад. Показывается, что у них разная толщина (обычно на лепке). 2 способа: 1. Условная мерка – палочка. Если проткнуть шар по вертикали и горизонтали, то толщина – одинаковая. Если проткнуть овалоид, толщина – разная. 2. С помощью ниточки – условной мерки можно обмотать шар сначала по вертикали, а затем по горизонтали, длина ниточки – одинаковая. Для овалоида понадобиться ниточка разной длины. Пример ознакомления с кругом. 1 этап (1-3 года). Предлагаются игры с геометрической мозаикой (содержащей круги) по составлению из фигур различных предметов (тележка, машинка и т.д.). Обращается внимание на то, что колеса должны быть круглыми, чтобы машинка могла ехать. Можно предложить просто покатать круги. Ведется работа по введению в словарь термина «круг». 2 этап (3-6 лет). Для сравнения круга и квадрата используется осязательно-двигательное обследование пальчиком их контуров (у круга дорожка гладенькая, а у квадрата есть препятствия, они острые). Просим детей проследить зрением за движением пальчика по контуру. Затем предлагаем положить круг на квадрат, обращаем внимание на лишние кусочки у квадрата. Просим покатать круг и квадрат: круг катится, квадрат – нет. Упражнения на группировку. Из квадратов и кругов строим поезд: что выбрать для колес, а что для окошечек? Затем в 3-4 года с кругом сравнивается треугольник, аналогично как с квадратом. В 4-5 лет с кругом сравнивается овал. Сначала круг накладывается на овал, указываются лишние кусочки. Затем демонстрируется более точный способ показа отличия этих фигур. Вводится понятие «оси» и путем измерения осей показывается, что у круга все оси равны. Затем демонстрируется, что при сгибе круга по оси границы совпадают. В 5-6 лет круг сравнивается с шаром. Показывается, что круг прячется в ладошки, значит он - плоский, а шар – не прячется, значит он - объемный. Затем демонстрируется, что шар легко катится в разные стороны, а круг лишь в две (его нужно придерживать). Обращается внимание, что шар – пространственный аналог круга. Для того, чтобы нарисовать предметы, имеющие форму шара, надо нарисовать круг. 3 этап (5-6 лет) 1. Обобщение понятия «круг». Детям предлагаются круги разного цвета и размера, необходимо назвать их одним словом. Упражнения на группировку: - выбрать круги из всех фигур; - выбрать круги из фигур без углов; - сгруппировать круги по цвету или размеру. 2. Определение формы окружающих предметов. Детей учат находить круглые предметы в определенной обстановке. Используются предметы, приближенные к плоским (колесо, блюдечко, поднос, салфетка, настенное панно, циферблат часов, зеркальце). Выясняется, что у этих предметов общее. Предлагается назвать предметы, имеющие форму круга. |
