3.Конспекты лекций Н. Конспекты лекций по дисциплине Теория и методика формирования элементарных математических представлений у детей дошкольного возраста

• Название: Конспекты лекций по дисциплине Теория и методика формирования элементарных математических представлений у детей дошкольного возраста
• Анкор: 3.Конспекты лекций Н.doc
• Дата: 13.12.2017
• Размер: 0.85 Mb.
• Имя файла: 3.Конспекты лекций Н.doc
• Тип: Конспект; #11208
• страница: 2 из 21

1.1.1. Этапы исторического развития числа

1 этап. Сравнение групп предметов по количеству с помощью установления взаимнооднозначного соответствия между элементами множеств (1 шкура - 1 горшок).

2 этап. Использование множеств-посредников для сравнения по количеству (зарубки на палке о количестве в прошлом году).

3 этап. Использование универсальных множеств для обозначения кол-ва (1 луна; 5 пальцев на руке: луна оленей; рука оленей).

4 этап. Возникновение числительных и нумерации, абстрагирование числа от конкретного множества.

5 этап. Становление теорий числа: количественной и порядковой.

1.1.2. Основные идеи количественной и порядковой теорий натурального числа

Количественная теория.

Г. Кантор, XIX в. Основные понятия – множество, взаимнооднозначное соответствие.

В том случае, если каждому элементу множества Х соответствует единственный элемент из множества У, то говорят, что между этими множествами установлено взаимнооднозначное соответствие.



Х У





Рассмотрим 2 бесконечных множества:

(1) множество натуральных чисел 1, 2, 3, 4, 5,…n, …

(2) множество четных натур. чисел 2, 4, 6,…2n, …( подмножество (1));

Так как ряд четных чисел можно пронумеровать с помощью натуральных чисел, то между этими двумя множествами можно установить взаимнооднозначное соответствие. Если между множеством и его некоторым подмножеством нельзя установить взаимнооднозначное соответствие, то множество является конечным.

Если между двумя конечными множествами можно установить взаимнооднозначное соответствие, то эти множества называются равночисленными.

Отношение «быть равночисленными» на множестве всех множеств является рефлексивным, симметричным, транзитивным, а значит, является отношением эквивалентности. Поэтому отношение «быть равночисленным» разбивает множество всех множеств на классы. В эти классы попадут самые различные множества. Общее между ними – одинаковое количество элементов (в класс «5» - 5 цветов, 5 пальцев).

Натуральным числом называют общее свойство класса не пустых, конечных, равночисленных множеств.

Покажем, как операции над числами определяются через операции над множествами.

Обозначим через n(А) количество элементов в множестве А.

Введем операцию сложения над числами через операцию объединения над множествами.

Суммой чисел a и b называется количество элементов в объединении множеств А и В, которое равно

а + b = n(АВ) = n(А) + n(В), при условии, что АВ = .

Порядковая теория натурального числа.

Джузеппе Пеано, XIX в. Основные понятия: единица (е), операции: непосредственно следовать за, сложение, умножение.

В основе теории – аксиомы Пеано, которые являются свойствами натурального ряда чисел.

1 аксиома. Единица непосредственно не идет ни за каким натуральным числом.

2 аксиома. Любое натуральное число непосредственно следует не более, чем за одним натуральным числом.

3 аксиома. Если к натуральному числу х добавить 1, то получим непосредственно следующее натуральное число х`, т.е. х + 1= х`.

4 аксиома. С помощью добавления единицы к натуральному числу можно получить весь ряд натуральных чисел.

5 аксиома. Если натуральное число х умножить на 1, то получим само натур. число, т.е. х∙1 = х.

х + у` = х + (у + 1) = (х + у) + 1 = (х + у)`

Мы видим, что в количественной теории понятие числа определяется через множество, а операции над числами - через операции над множествами. В порядковой теории дан принцип образования каждого числа, понятие числа определяется через систему аксиом.

Познание ребенком понятия числа происходит одновременно в рамках количественной и порядковой теорий.

1.1.3. Нумерации

Нумерация - графическое изображение числа.

Существуют разные способы изображения числа. У разных народов в разное время существовали разные способы изображения чисел:

1. 
   Иероглифическая нумерация (Др. Египет) – числа изображались с помощью рисунков.
   
2. 
   Клинопись (Вавилон) – использовались горизонтальные и вертикальные клинышки.
   
3. 
   Буквенная нумерация – числа изображались в виде букв, первая буква числительного (penta - p).
   
4. 
   Алфавитная нумерация: а) греческая; б) славянская.
   

Первые 9 чисел – обозначаются первыми 9 буквами алфавита; следующие 9 букв обозначают десятки; следующие – сотни. Чтобы запись числа отличалась от записи букв, ставилась титла – волнистая черточка над буквой.

5. 
   Римская нумерация. Для записи числа использовались 7 знаков:
   

I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000. Все остальные числа записывались с помощью этих знаков на основе следующих правил:

Если низшее число написано справа, то его прибавляют: VI; если низшее число написано слева, то его отнимают: IV .

Прибавлять можно не более 3-х знаков, а отнимать не более одного: VIII – восемь, IX – девять.

Отнимать можно непосредственно предыдущий знак, от сотни – только 10, от 500 – только 10. Например, 99 – XCIX.

Если надо записать число более 3-х тысяч, мы записываем его низшими знаками, берем в скобки и обозначаем индексом m. 214698 – (CCXIV)_m DCXCVIII.

6. Арабская нумерация (пользуемся и теперь). Придумали в Индии, европейцы переняли у арабов. Используется 10 знаков – цифры: 0, 1, …., 9.

1.1.4. Системы счисления

Система счисления – это совокупность способов записи чисел и выполнения действий над числами.

Различают позиционные и непозиционные системы счисления. В позиционных – значение каждого знака в записи числа зависит от занимаемой им позиции (222), а в непозиционной – не зависит (CCXXII).

К позиционным системам счисления относятся: десятичная (используется 10 знаков для записи чисел – 0, 1, 2, …, 8, 9), двоичная (используется 2 знака – 0, 1) и т.п.

Правила перевода чисел из одной системы счисления в другую.

А) Чтобы перевести число из любой позиционной системы счисления в десятичную, надо представить это число в стандартном виде (например,

в десятичной системе счисления, 2134 = 2∙10³+1∙10²+3∙10¹+4∙10⁰,

в двоичной системе счисления, 1101₂ = 1∙2³ + 1∙2² + 0∙2¹ +1∙2⁰,

затем выполнить все действия: 1101₂ = 1∙2³ + 1∙2² + 0∙2¹ +1∙2⁰ = 8+4+0+1= 13.

Полученный результат и будет искомой записью числа в десятичной системе счисления, т.е. 1101₂ = 13.

Б) Чтобы перевести число из десятичной системы счисления в любую позиционную, надо делить это число на основание системы до тех пор, пока делимое не станет меньше делителя. Затем надо записать все остатки снизу вверх (или справа налево).

13│2

Полученный результат и будет искомой записью числа, 1 6│2

т.е. 13 = 1101₂. 0 3│2

1 1│2

1

Арифметические действия с многозначными числами в любой позиционной системе счисления выполняются также как и в десятичной, т.е. числа записываются в столбик разряд под разрядом. А для выполнения действий с однозначными числами

а\в	0	1
0	0	1
1	1	10

составляются таблицы. Например, в двоичной системе счисления:

₊111₂

101₂

1100₂
Из истории происхождения систем счисления

Одними из первых появились пятеричная и десятичная системы счисления (по количеству пальцев на одной или двух руках). Существовала также двенадцатеричная и шестидесятеричная системы счисления. В первой из них считали большим пальцем фаланги остальных четырех пальцев. Отголоски этой системы дошли до наших дней: посуда группируется по 12 приборов (в дюжины). Гипотеза появления шестидесятеричной системы счисления такова: объединились два народа, у одного из которых была пятеричная, а у другого двенадцатеричная системы счисления. В наше время свидетельством существования этой системы служит состав часа из 60 минут и т.п.

1.2. Теория множеств

1.2.1. Множество. Отношения между множествами

Множество – одно из основных математических понятий. Множество ассоциируется с понятием группа. Множества могут быть конечными, бесконечными, пустыми.

Пустым называется множество, которое не содержит ни одного элемента ().

Множества обозначаются большими буквами латинского алфавита А, В, С,…, а элементы - маленькими буквами а, в, с, ….х, у.

«Элемент а принадлежит множеству А» записывают так: а  А, если не принадлежит – то в  А.

Способы задания множества:

1) путем перечисления всех элементов А = {а, с},

2) путем задания характеристического свойства.

Характеристическое – такое свойство, которым обладает каждый элемент данного множества, и не обладают элементы, не принадлежащие данному множеству.

Например, «натуральные числа больше 3» можно задать так: А = {n N, n >3}.

Отношения между множествами

Множества изображаются на плоскости с помощью кругов Эйлера.

1. Отношение равенства

Говорят, что А=В, если все элементы множества А принадлежат множеству В и наоборот, все элементы множества В принадлежат множеству А.

Ни количество элементов, ни порядок их следования не имеет значения для равенства множества.

Пример: А={1; 2} и В={1, 2, 2, 1}, А=В.

2. Отношение включения

Г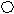оворят, что множество А включено ( ) в В, если все элементы множества А принадлежат В.
В этом случае множество А будем называть подмножеством В.

Если А={1, 2}, В={1, 2, 3}, то АВ.

Если А - студенты дошфака, В - студенты университета, то АВ.

3. Отношение пересечения

Говорят, что множества А и В пересекаются, если имеют хотя бы один общий элемент.

Например, А={1, 2, 3} и В={2, 4, 6} , А и В - пересекаются.

А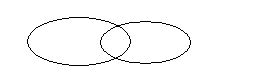В

4. Если АВ=, то множества А и В не пересекаются. Например, студенты 1 и 5 курсов – не пересекающиеся множества.

А В

1.2.2. Операции над множествами

Результатом операций над множествами всегда является множество.

1. Пересечением множеств А и В называется такое множество, которое состоит из элементов, принадлежащих множеству А и принадлежащих множеству В (т.е. их общих элементов). Например:

а) А={1, 2, 3}, В={2, 4, 6},

А  В ={2}.

б) А={1, 2}, В={3, 4}, А  В= .

в) А={1, 2}, В={1, 2, 3},

А  В ={1, 2}=А.

г) если А = В, то А  В=А=В.

2. Объединением множеств А и В называют такое множество, в которое входят элементы множества А или множества В ( т.е. все элементы А и все элементы В). Например:

а) А={1, 2, 3}, В={2, 4, 6},

А  В={1, 2, 3, 4, 6}

б) А={1, 2}, В={3, 4},

А  В={1, 2, 3, 4}.

в) А={1, 2}, В={1, 2, 3},

А  В={1, 2, 3}.

г) если А = В, то А  В=А=В.

3. Разностью множеств В и А называют множество, которому принадлежат все те элементы множества В, которые не принадлежат А. Например:

а) А={1, 2, 3}, В={2, 4, 6},

В\ А={4, 6}.

б) А={1, 2}, В={3, 4};

В\ А={3, 4}.

в) А={1, 2, 3}, В={1, 2};

В \ А= Ǿ.

с) если А=В, то В\ А= Ǿ.

4. В случае, когда А  В, можно рассмотреть частный случай разности множества В и А. Дополнением множества А до множества В называется такое множество, которому принадлежат все те элементы множества В, которые не принадлежат А.

5. Декартовым произведением множества А на множество В называется множество всевозможных пар, первый элемент которых принадлежит множеству А, а второй - множеству В.

А х В = {(а, в), а  А, в  В}.

Пара – упорядоченное множество, состоящее из двух элементов.

А={1, 2}, В={3, 4}, А х В= {(1, 3), (1, 4), (2, 3), (2, 4)}.

Свойство переместительности.

Для операций пересечения и объединения выполняется свойство переместительности, т.е.

А  В = В  А; АВ = В  А. (На картинке заштрихованные разными цветами области совпадают).

Для операций разности и декартового произведения свойство переместительности не выполняется.

А\ В  В\ А. Пусть А={1, 2, 3}, В={2, 4, 6},

тогда В\ А={4, 6}, а А\ В={1, 3}.

А х В  В х А. Пусть А={а, о}, В={н, м},

тогда АхВ={ан, ам, он, ом}, а ВхА={но, на, мо, ма}.

1.2.3. Отношения между элементами множества. Свойства отношений

Примеры отношений:

– между числами: =, , 

– между прямыми в пространстве: ||, .

– пространственные отношения между предметами: слева, справа, далеко, близко;

– родственные отношения между людьми: быть братом.

Рассмотрим определение отношения на примере. Зададим отношение «Город а стоит на реке в». Для этого зададим следующие множества: А – множество городов, А= {Б, К, Г}; В – множество рек, В = {М, Д, С}.

Найдем декартово произведение множества А на В.

А  В = {(Б,М); (Б,Д); (Б,С); (К, М); (К, Д); (К,С); (Г, М); (Г,Д); (Г,С)}.

Теперь найдем такое подмножество декартового произведения, где на первом месте в паре стоит горд, а на втором – река, на которой этот город расположен.

Р = { (Б; М); (К; Д); (Г,С) }, Р  А  В.

Для того, чтобы задать отношение между городами и реками «Город а стоит на реке в» необходимо задать 3 множества: множество городов, множество рек и подмножество декартового произведения А на В.

Другие примеры: сетка занятий в д/с; график дежурств.

Определение: Говорят, что между элементами множеств А и В задано отношение , если заданы 3 множества А, В, Р  А  В.

Способы задания отношений

1) Путем перечисления всех элементов отношения (т.е. всех пар).

Рассмотрим множество А = {1, 2, 3, 4}. Зададим отношение «». Первый элемент в парах должен быть меньше второго. Р = {(1;2), (1;3), (1;4), (2;3), (2;4), (3;4) }.

2) Путем задания характеристического свойства. Характеристическое свойство имеет вид предложения с 2-мя неизвестными. «Число х меньше числа у»

3)С помощью графа. Граф – это изображение элементов множества на плоскости с помощью точек и изображение отношений между элементами множеств с помощью стрелок.

4) С помощью графика в декартовой системе координат, где 1-ый элемент - абсциссы, 2-ой – ординаты.

Свойства отношений.

Свойство рефлексивности. Отношение  на множестве Х называется рефлексивным, если каждый элемент х из множества Х находится в отношении  с самим собой, т.е. х  х.

Например: В качестве Х рассмотрим множество фигур. В качестве отношения  рассмотрим отношение «быть одинаковым по форме». Каждая фигура одинакова по форме сама с собой - это утверждение истинно. Значит отношение «быть одинаковым по форме» на множестве всех фигур является рефлексивным.

1. 
   Свойство антирефлексивности. Отношение  на множестве Х называется антирефлексивным, если каждый элемент х из множества Х не находятся в отношении  с самим собой, х  х.
   

«Каждое число не меньше самого себя». Утверждение истинное. Следовательно, отношение «меньше» на множестве чисел является антирефлексивным.

2. 
   Свойство симметричности. Отношение  на множестве х называется симметричным, если для любых элементов х, у из множества Х справедливо: если х находится в отношении  с у, то у находится в отношении  с х т.е. если х  у, то у  х.
   

Например: Если фигура а одинакова по форме с фигурой в, то фигура в одинакова по форме с фигурой а. Вывод: утверждение справедливо. Значит, отношение «быть одинаковым по форме» является симметричным на множестве фигур.

4) Свойство антисимметричности. Отношение  на множестве Х называется антисимметричным, если для  не равных друг другу элементов из множества Х справедливо утверждение: Если х  у, то у  х.

Например: отношение «меньше» на множестве чисел, ав.

«Если ав, то ва» - истинно, значит, отношение «меньше» является антисимметричным на множестве чисел.

5)Свойство транзитивности. Отношение  на множестве Х называется транзитивным, если для  элементов х, у, z множества Х справедливо утверждение: если х  у, у  z, то х  z.

Например, «если фигура а одинакова по форме с фигурой в, и фигура в одинакова по форме с фигурой с, то фигура а одинакова по форме с фигурой с» - справедливо. Значит, отношение «быть одинаковым по форме» является транзитивным

1.2.4. Отношения эквивалентности и порядка

Любое отношение не может быть одновременно симметричным и антисимметричным, рефлексивным и антирефлексивным, но существуют отношения, которые могут быть одновременно рефлексивными, симметричными, транзитивными.

Определение. Отношение  называется отношением эквивалентности, если оно одновременно является рефлексивным, симметричным, транзитивным.

Отношения, которые близки по смыслу слову «равный» являются эквивалентными. Например, отношение равенства между числами или «быть одинаковой формы» между фигурами.

Определение. Отношение  называется отношением порядка, если оно одновременно является антирефлексивным, антисимметричным, транзитивным.

Множество, на котором задано отношение порядка, называется упорядоченным.

Все отношения, близкие по смыслу отношению «следовать за» являются отношениями порядка. Например, отношение «» на множестве чисел («выше» на множестве людей).

1.2.5. Разбиение множества на классы

Пример: рассмотрим множество М– множество разноцветных фигур; подмножество А – множество красных фигур, В – не красные фигуры. А  М, В = М \ А, В  М М


Подмножества А и В не являются пустыми. Они не пересекаются, и объединение их есть М.

При выполнении этих условий мы говорим, что множество М разбито на 2 класса: красных фигур и не красных

Общее определение. Говорят, что множество М разбито на классы (попарно не пересекающиеся подмножества) если выполнены 3 условия: все подмножества множества М не пусты, все подмножества множества М не пересекаются, объединение всех подмножеств множества М есть само множество М.

Разбиение множества на классы лежит в основе операции классификации.

Всякое отношение эквивалентности разбивает множества на классы и наоборот, разбиение множества на классы определяет отношение эквивалентности.

Если отношение не является отношением эквивалентности, то оно не разбивает множество на классы.

1.3. Возрастные особенности развития количественных представлений у детей

Возрастные особенности развития математических представлений у детей дошкольного возраста будем рассматривать в соответствии с исследованиями А.М. Леушиной.

1. 
   Представления о множестве объектов
   

Множество предметов и явлений ребенком воспринимается различными анализаторами.

1-2 года. К 1-2 годам у детей накапливаются представления о множестве однородных предметов, которые отражаются в пассивной речи детей (построить домик и домики – единственное и множественное число).

Затем в активной речи дети начинают использовать множественное и единственное число. На этом этапе множество еще не имеет четких границ для ребенка и не воспринимается элемент за элементом, не осознается количественная сторона множества.

Дети понимают смысл слова «много» и «мало», но эти слова не имеют четкой количественной характеристики, ассоциируются со словами «большой», «маленький».

2-3 года. Дети воспринимают множество в его границах, умеют сосредотачивать свое внимание на границах множества, а четкое понимание внутренних элементов еще отсутствует. При наложении предметов на рисунки дети заполняют всю часть карточки между крайними элементами, но не воспринимают количество. Легче воспринимают множество, если оно расположено линейно, в ряд.

3-4 года. Ребенок становится более требовательным к однородному составу множества, т.е. он считает, что множество всегда состоит из однородных элементов и что оно конечно. На восприятие множества еще оказывают влияние качественно-пространственные признаки (форма, величина, расстояние между элементами, расположение по-разному в пространстве).

При наложении ведущим для детей является изображение, пространственное отношение не играет существенной роли. Прием наложения способствует формированию представлений о множестве как структурно-замкнутом целом, состоящим из отдельных элементов. Общее количество элементов при использовании этого приема не определяется. Более трудным является прием приложения. Здесь ребенок должен точно воспроизвести то количество элементов, которое образует данное множество. Для этого ребенку надо воспринять не только изображения, но и простые отношения между ними, а это для ребенка трудно.

Уже в дочисловой период ребенок может опознать группу без счета, если она стандартна, постоянна. Вероятно, другие предметы в том же количестве ребенок сосчитать еще не сможет.

4-5 лет. На этом этапе восприятие только однородных множеств играет отрицательную роль, поэтому необходимо предлагать детям производить различные операции с множествами: составлять единое множество из 2-х групп, каждая из которых обладает своими качественными особенностями, несущественными для всего множества в целом.

2. 
   Развитие у детей деятельности счета
   

Счет – математическое понятие, это операция, имеющая целью установить, сколько элементов содержит данное конечное множество.

1,5-2 года. Дети сопровождают свои операции с множеством такими словами как «вот», «еще» или числительными в любом порядке. Каждое повторение ребенок соотносит с одним предметом и одним движением, тем самым он устанавливает взаимнооднозначное соответствие между количеством предметов и количеством слов, движений.

2-4 года. Появляется интерес к сравнению групп множеств путем установления взаимнооднозначного соответствия. Последовательное называние числительных еще не означает овладение процессом счета, т.к. ребенок не понимает итога счета, т.е. не умеет отвечать на вопрос «сколько?» Счет еще не служит средством определения количества. Чаще всего названное числительное служит сигналом к остановке называния числительных.

4-5 лет. Дети начинают употреблять числительные в определенном порядке и отличать итог счета от процесса счета. Начинают понимать, что равночисленные множества всегда именуются одним числом.

5-6 лет. Усваивают последовательность называния числительных, понимают, что количество не зависит от направления счета, что число является показателем количества, осознают отношения между числами, т.е. осваивают обратный счет.

6-7 лет. Овладевают счетом группами, т.е. понимают, что единицей счета может быть не только отдельный предмет, а целая группа.

7-8 лет. Овладевают счетом десятками и новой деятельностью – вычислением. Счет связан с конкретным множеством, с определением количества в определенном множестве, а вычисление – абстрактная операция, здесь участвую только числа (без называния предмета).

3. 
   Развитие понятия числа
   

3-4 года. Дети используют слова-числительные, но не понимают, что такое число. На этом этапе дети способны лишь сравнивать различные множества путем установления взаимнооднозначного соответствия.

4-5 лет. Дети могут сравнивать числа на основе сравнения множеств, но не воспринимают число абстрактно, без множества.

5-6 лет. Способны сравнивать любые числа на основе свойства транзитивности. При измерении понимают число как результат измерения, т.е. как отношение всей величины (целого) к условной мерке (части). Понимают, что число служит лишь показателем количества. Происходит абстрагирование числа от конкретных множеств.

1.3.4. Развитие представлений о натуральном ряде чисел

Натуральный ряд – последовательность целых положительных чисел, расположенных в порядке их возрастания.

2-4 года. На основе речи взрослых дети начинают рано употреблять слова-числительные: сначала хаотично, затем упорядочено. Осознание порядка следования чисел происходит сразу в 2-х направлениях:

- увеличиваются последовательности чисел, которые дети запоминают,

- начинают осознавать, что каждое числительное всегда занимает свое определенное место, но на этом этапе не понимают, почему это происходит.

У детей образуются рече-слухо-двигательные связи между называемыми числительными. Ребенок называет ряд натуральных чисел подобно бессмысленной считалке и не может продолжить ряд чисел с середины, т.к. дети не понимают отношений между числами.

4-5 лет. Дети не всегда могут ответить на вопрос, какое число идет до этого, а какое после. Не могут назвать предыдущие числа. Для них ряд движется как бы вперед (понимают только последние числа). Такое представление о натуральном ряде называется «пространственным образом натурального ряда чисел». Чтобы найти число на единицу больше дети мысленно или вслух начинают называть слова-числительные от начала ряда. Таким образом, разностные отношения между предыдущими и последующими числами еще не усвоены.

5-6 лет. Эмпирические представления о натуральном ряде как пространственном образе перестраиваются в понятие о натуральном ряде чисел. Дети начинают осознавать основной принцип построения натурального ряда

(п` = п + 1).
1.4. Методика формирования количественных представлений

1. Формирование умения группировать предметы (2- 6 лет)

1 этап. Выделение, нахождение и называние признаков предметов.

Сначала учат группировать по одному признаку, при этом все остальные признаки должны отсутствовать или быть несущественными для детей. Признак, по которому предлагается группировка предметов, усложняется с возрастом (цвет–название–величина–форма–количество–характерные функции). Например:

- все машинки поставьте на нижнюю полку, а куклы - на верхнюю (по названию).

- у детей геометрические фигуры одного цвета, но разной формы, надо построить башенки из кубиков (или цилиндров).

2 этап. Группировка по двум - трём и более признакам.

При этом предметы должны отличаться только по этим признакам или другие признаки должны быть несущественны. Например:

- взять для постройки красные большие кубики (а фигуры отличаются по форме, цвету, величине),

- построить цепочку так, чтобы фигура отличалась по величине и форме.

3 этап. Группировка предметов по образцу.

Признаки словесно не указываются, предметы должны отличаться по нескольким признакам, дети должны сами найти общие признаки и провести группировку.

Например: принести на стол вот такие игрушки.

4 этап. Группировка по заданному признаку.

Предметы отличаются по нескольким признакам, но указывается лишь один.

Наиболее легкие признаки – цвет и название. Наиболее сложные – функции предмета. Например:

- Назвать предметы формы круга.

- Собрать и положить в тазик игрушки, которые можно мыть.

2. Формирование представлений о множественности и единичности предметов (с 3 до 5 лет)

С детьми проводятся упражнения или игры, в которых показывается, что множество состоит из отдельных элементов. Детям показывают, как образуется множество и как множество разбивается на отдельные элементы.

Для начала берется множество однородных предметов. Акцентируется внимание на словах: «Сколько?», «Много», «Один», «Ни одного».

Например: дети собирают листья, воспитатель отбирает однородные листья по количеству детей и говорит:

- У меня много листьев. – Сколько у меня листьев? (Много.)

- Я раздаю по одному. Тебе один, тебе один, тебе один. Листьев становиться все меньше и меньше. У меня не осталось ни одного. Сколько у тебя листьев? (Один.) Сколько у меня? (Ни одного.)

- Я собираю листья: один у тебя, один у тебя, один у тебя. У меня становится листьев все больше и больше. Снова у меня много листьев. Сколько у меня листьев? А сколько осталось у тебя?

Такое упражнение проводится с разными видами предметов несколько раз.

Позже эта задача решается с неоднородными множествами. В 5 – 6 лет детям показывается, что группировать предметы можно по разным признакам, не принимая во внимание несущественные признаки.

Например: предметы разного цвета и разной формы. Дети должны сосчитать предметы названной формы. Обычно дети сосчитывают отдельно предметы каждого цвета. Воспитатель учит принимать во внимание лишь заданный признак, не обращая внимание на другие. Например: посчитать, сколько синих фигур (надо посчитать и круги, и квадраты).

3. Формирование умения выделять 1 и много предметов в окружающей обстановке (с 3 до 4 лет)

1 этап. Один и много предметов расположены на различных плоскостях (2 разных стола, 2 обруча). Вопросы и задания:

- покажи, где один, а где много,

- сколько предметов на красной полоске, а сколько на синей?

2 этап. Один и много предметов расположены вперемешку на одной плоскости (зайчики и 1 белочка). Вопросы: каких предметов много, а какой один, сколько зайчиков, сколько белочек?

3 этап. Предлагается упражнение, где в одном объекте заключено много предметов (одно дерево, а на нем много листьев; один аквариум – много рыбок).

4 этап. Один и много предметов не ограничены ни плоскостями, ни одним объектом. Дети должны мысленно объединить их в группу. Например: по одной кукле на стуле, ковре, шкафу, а всего - много кукол.

Игры на всех 4-х этапах (отличие лишь в расположении наглядного материала):

- «Путешествие» или «Поезд с остановками» (Воспитатель выясняет, сколько предметов на станции. Если на все вопросы дети ответили, то едут к следующей станции).

- «Магазин игрушек» (Разных игрушек должно быть разное количество. Дети должны сами сказать, сколько хотят купить игрушек).

- «Зоопарк» (разное количество животных в клетках).

4. Формирование умения сравнивать 2 группы предметов по количеству, путем установления взаимнооднозначного соответствия (c 3 до 6 лет)

Существуют 6 приемовустановления взаимнооднозначного соответствия:

- наложение ( мл.возр.)

- приложение (мл.возр.)

- составление пар (мл. – ср.возр.)

- соединение стрелками (ср.возр.)

- использование множества-посредника (ст.возр.)

- счет (ср.- ст.возр.)

Наложение. Наглядный материал: карточки с изображенными предметами (3 -5 шт.), расстояние между предметами должно равняться самим предметам, для наложения даются мелкие предметы, которые должны быть связаны с рисунками по смыслу.



Начинать нужно с проблемной ситуации. «Хватит ли всем бабочкам по цветочку, т.е. поровну ли у нас бабочек и цветочков».

Методика: Воспитатель раскладывает бабочки правой рукой слева направо точно одну бабочку на один цветочек. Останавливаясь на каждой паре, обращает внимание, что на каждом цветочке сидит одна бабочка, что между цветочками бабочку не кладем, оставляем пустое место. «У нас бабочек столько же, сколько цветочков, каждой бабочке хватило по цветочку, бабочек и цветочков поровну, одинаковое количество. Поровну ли бабочек и цветочков?» После демонстрации приема наложения детям даем упражнения, в которых они учатся сравнивать 2 группы предметов по количеству с помощью этого приема.

Приложение. Используются карточки с двумя полосками. На верхней – предметы, а нижняя – пустая. Для приложения подбираются предметы, которые подходят по смыслу.




Методика обучения приему приложения основывается на знании детьми приема наложения. Например, на верхней полоске раскладываем грибочки. Затем создаем ситуацию: на грибочки упали листики. Листики накладываем на грибочки и выясняем: поровну ли их. Затем перетягиваем последовательно каждый листик на нижнюю полоску: «подул ветер». Под каждым грибочком лежит только один листик. Между листиками - пустые места. «Поровну ли теперь листиков и грибочков? Если под одним грибочком лежит один листик, то грибочков и листиков поровну».

Упражнение: положить листиков на нижнюю полоску столько, сколько на верхней грибочков. Если дети затрудняются, то делим вертикальными линиями карточку на клетки или можно провести стрелки от предметов верхней полоски на нижнюю.

Составление пар. Этот прием аналогичен приложению, но не применяются карточки. Используются предметы, связанные между собой по смыслу. Вначале предметы расставляем в ряд. Например, конфетами угощаем кукол. В дальнейшем не обязательно в ряд (можно по кругу). Воспитатель выясняет, поровну ли, например, белочек и зайчиков. Для проверки ответа необходимо одну белочку поставить около одного зайчика.

Соединение стрелками. Детям предлагается такая ситуация, в которой нельзя воспользоваться известными им приемами (Нарисован торт и дети. «Хватит ли всем детям по кусочку торта?»). На рисунке соединяем одного ребенка с одним кусочком торта. Если лишних детей не осталось, то всем хватило.

Использование множества-посредника. Создаем ситуацию, когда нельзя использовать известные детям приемы. Например: с одной стороны детского сада растут деревья, с другой – тоже. Где растет больше деревьев? Используем множество-посредник - камешки. Раскладываем один камешек под одним деревом. Сначала под предметами одного множества, затем под предметами второго множества. Делаем вывод о равенстве или неравенстве предметов по количеству.

Каждый из этих приемов даем в два этапа. Сначала формируем у детей представление об отношении равенства («поровну»), для этого берем равночисленные множества. А на втором этапе формируем представление об отношениях «больше» и «меньше». Понятие «больше» поясняем через слово «лишний», а «меньше» - через «не хватает».

5. Методика обучения счету (4 - 6 лет)

Единого мнения по обучению детей счёту не существует. Леушина А.М. считала: не надо спешить, надо начинать учить считать после обучения операциям над множествами.

Перед тем, как обучать детей счету, необходимо создавать ситуации, в которых дети сталкиваются с необходимостью умения считать.

Обучение счету происходит на основе сравнения двух групп предметов по количеству.

1 этап. Воспитатель сам ведет процесс счета, а дети повторяют за ним итоговое число. Показывается независимость числа предметов от других признаков предметов.

2 этап. Воспитатель учит детей процессу счета и знакомит с образованием каждого числа, учит сравнивать смежные числа. Сначала детей учат считать в пределах 3, а потом в пределах 5, затем - 10 (по пр. «Пралеска»), по программе «Радуга» - до 20 (на седьмом году жизни). М. Монтессори разработала методику и материал для обучения счету в пределах 1000.

Рассмотрим пример обучения счету до трёх.

На 1 этапе воспитатель предлагает детям две группы предметов, расставленные в два параллельных ряда, расположенные один под одним (зайчики и белочки). Вопросы:

- Сколько зайчиков (белочек)?

- Поровну ли зайчиков и белочек?

Далее добавляется один предмет к одному из этих

множеств (прискакал зайчик).

- Поровну ли сейчас белочек и зайчиков?

- Сколько было, сколько стало зайчиков?

Воспитатель сам ведет процесс счета («Один, два, три». Обводит рукой все множество. «Всего три зайчика»). Дети следят за процессом счета и повторяют итоговое число – «три».

Добавляем еще одну белочку.

- Поровну ли теперь зайчиков и белочек?

- Сколько стало белочек?

Воспитатель считает белочек (одна, две, три; всего три белочки). Согласовывает существительные и числительные в роде и числе. Дети видят, что числительное «три» является общим показателем количества для зайчиков и белочек.

На 2 этапе, обучая детей процессу счета, воспитатель побуждает их придерживаться следующих правил:

1. 
   Согласовывать каждое числительное с одним предметом и одним движением.
   
2. 
   Согласовывать числительное и существительное в роде, числе, падеже.
   
3. 
   После каждого числительного существительное не повторяем (чтобы процесс счета шел абстрактно).
   
4. 
   После называния последнего числительного необходимо обвести всю группу предметов круговым жестом и назвать итоговое число.
   
5. 
   Называя итоговое число, произносим соответствующее существительное.
   
6. 
   Счет необходимо вести правой рукой слева направо (чтобы у детей сложился стереотип).
   
7. 
   Нельзя вместо числительного «один» говорить слово «раз» для ответа на вопрос «сколько?».
   

Рассмотрим, как показать образование числа (например, числа 3).

Необходимо опираться на сравнение двух множеств по количеству. Вопросы:

- Сколько белочек? (две)

- Сколько зайчиков? (два)

Добавляем одного зайчика.

- Сколько стало зайчиков?

- Сколько было?

- Сколько добавили, чтобы стало 3?

- Как получить число 3? (Надо к двум добавить единицу, получим 3).

В дальнейшем (после того, как дети научатся считать до четырех) необходимо показать образование числа 3 путем уменьшения множества на единицу. Т.о., образование каждого числа показывается двумя способами, путем увеличения и уменьшения множества на 1.

6. Методика обучения отсчитыванию предметов (4 – 6 лет)

С помощью проблемной ситуации необходимо показать отличие процесса счета от процесса отсчитывания.

Сосчитать – это значит определить, сколько всего элементов в множестве.

Отсчитать – выделить указанное количество элементов из множества.

Правила счета и отсчитывания совпадают, однако при обучении отсчитыванию особое внимание следует уделить следующему правилу: числительное надо называть лишь на 1 момент движения.

Виды упражнений по отсчитыванию:

• 
  Отсчитывание по образцу (столько-сколько); сначала образец дается в непосредственной близости, а затем на расстоянии;
  
• 
  Отсчитывание по названному числу (или показанной цифре);
  
• 
  Детям старшего возраста предлагается запомнить 2 смежных числа и отсчитать 2 группы предметов (из корзины отсчитать 2 яблока и 3 груши); обращается внимание на то, чтобы дети запомнили какое количество предметов надо отсчитать (просим детей повторить названные числа).
  

7 . Методика обучения порядковому счету (4 – 6 лет)

1 этап. Сначала детям предлагаются подготовительные упражнения (с несколькими видами наглядного материала), в которых показывается, что для ответа на вопрос «сколько?» необходимо использовать числительные «один, два, три», т.е. количественные. При этом не важно, в каком направлении ведется счет и как предметы расположены в пространстве.

Затем знакомство с порядковым счетом проводится в процессе драматизации сказки («Теремок», «Репка», «Колобок»).

Воспитатель показывает детям, что для ответа на вопрос «Какой по счету?» используются порядковые числительные: первый, второй, третий и т.д.. Важно, чтобы предметы располагались линейно и указывалось направление счета.

Пример: сказка «Теремок».

Воспитатель выкладывает героев сказки. Выясняет сколько всего, предлагает детям сосчитать. Затем сам рассказывает, кто какой по счету пришел: первая – мышка, вторая - лягушка…. После этого задаются 2 вида вопросов:

- Кто пришел первым, вторым, третьим…?

- Каким по счету стоит мышка, ежик…? (указывается, что считать следует слева направо).

Затем предлагается ответить на те же вопросы, но счет вести справа налево.

После этого воспитатель подводит детей к тому, что определить место предмета среди других можно лишь, если герои стоят в ряд.

Для закрепления проводятся упражнения, в которых определяется: какой предмет каким по счету расположен. Например: в процессе ознакомления с геометрическими фигурами: «Как называется фигура, которая стоит на третьем месте?».

2 этап. Показывается детям, в каких случаях используются количественные, а в каких порядковые числительные. Предлагаются упражнения, в которых задаем 2 вопроса: «Сколько всего?» и «Какой по счету?». Следим, какие числительные используют дети. Поясняем, в каком случае, какие числительные надо произносить. Детей подводят к выводу, что для того, чтобы определить, сколько предметов, используют количественный счет, а чтобы определить место предмета среди других, используется порядковый счет.

Кроме таких упражнений важно создавать ситуации в повседневной жизни и играх, в которых дети видели бы отличия в использовании количественного и порядкового счета. Например, в игре «Театр» уточняем, что обозначает цифра на билете: сколько всего мест или какое по счёту указанное место.

Виды упражнений:

- определить номер указанного предмета;

- назвать предмет по указанному номеру.

Игра «Что изменилось?» (Выясняется, на каком месте расположена игрушка. Дается команда «Глазки спят». Затем воспитатель меняет место расположения игрушки. После слов «глазки открыли» предлагается тем, кто заметил изменения, поднять руку и ответить: какой по порядку эта игрушка стояла раньше, а какой стоит сейчас).

8. Методика ознакомления с цифрами (3 – 5 лет)

Ознакомление с названием и внешним видом цифры идет в возрасте до четырёх лет, а после обучения счету детей знакомят с сущностью цифр.

1 этап.

• 
  Воспитатель в различных ситуациях знакомит детей с именем и внешним видом цифры (в процессе прогулки обращает внимание на номера домов, машин; на номера страниц).
  

• 
  Воспитатель читает стишки, в которых описывается внешний вид цифр . (С.Маршак «Веселый счет», Г. Виеру «Считалочка»).
  

2 этап: (ср.возр.)

Как только дети научились считать в соответствующих пределах, их необходимо познакомить с сущностью каждой цифры последовательно. Предлагается обозначить в группе количество предметов разными способами: соответствующим количеством счетных палочек, соответствующей числовой карточкой, и, наконец, с помощью цифр.

Можно предложить детям рассмотреть таблицу, где нарисовано одно и то же количество разных предметов и все они обозначены одной цифрой.

Подводим детей к тому, что одинаковое количество предметов всегда обозначается одной и той же цифрой. Отличие понятия «число» и «цифра» (лiк – число, лiчба - цифра): цифра - значок или рисунок, с помощью которого можно написать число или указать количество предметов. Надо понимать, что число изображается не только с помощью цифры. Можно познакомить детей с римской нумерацией – изображением числа с помощью рисунков. Или предложить цветные числа – палочки Кьюизенера.

Упражнения на закрепление сущности цифр:

- Подобрать цифру для соответствующего множества.

- Создать (найти) группу предметов, соответствующую по количеству показанной цифре.

И
.

.
гры:

«Найди пару» (лото).

«Найди свой домик».

Знакомство с цифрой 0.

Детям предлагается 3 блюдца: на одном - 3 предмета, на другом - 5, на третьем - ни одного. Просим обозначить с помощью цифр количество предметов в каждом блюдце. Дети могут сообразить, что на пустое блюдце надо положить «0». Если дети затрудняются, то воспитатель читает стихотворение про «0»: Цифра вроде буквы «О» - это «ноль» иль «ничего».

А затем поясняем, что отсутствие предметов также обозначаем цифрой, это – цифра «0».

Знакомство с изображением числа 10.

Надо показать детям, что число 10 изображается с помощью двух цифр «1» и «0». Воспитатель читает соответствующий стих.

Круглый ноль такой хорошенький, но не значит ничегошеньки.

Ну, а если рядом с ним единицу примостим –

Он побольше станет весить, потому что это - десять. (С.Я.Маршак)

Для закрепления подходят те же игры, что и для других цифр. В игры и упражнения включаем 0 и 10.

9. Формирование представлений о составе числа из отдельных единиц в пределах 5 (5 – 6 лет)

Эта задача является подготовительной для обучения операциям над числами.

Наглядный материал должен отличаться хотя бы по 1-му признаку (видовому) и быть однородным.

Методика: детям предлагается 3 (4, 5) предметов (например, флажки разного цвета) и задаются следующие вопросы:

- Сколько всего предметов?

- Сколько предметов одного вида? (Сколько красных флажков? Сколько синих флажков? Сколько зеленых флажков?)

Вывод: у нас всего 3 флажка: 1 красный, 1 зеленый, 1 синий.

Аналогичная работа проводится еще с двумя видами наглядного материала, а затем делается обобщающий вывод: 3 это 1, 1 и 1. Для закрепления предлагается назвать разные предметы (например, овощи), чтобы их всего было 3.

Аналогичным образом рассматривается состав чисел 4 и 5.

Для закрепления предлагаются игры: «Я знаю 5 имен девочек», «Назови 5 разных предметов мебели (овощей)», «Кто быстрее назовет».

На первых порах детям разрешается загибать пальчики или называть слова-числительные, но к 6 годам дети должны научиться в уме удерживать состав числа.

10. Формирование представлений о составе целого множества из частей (5 – 6 лет)

Эта задача решается с целью подготовки детей к пониманию состава числа из меньших чисел. Воспитатель берет два равночисленных множества однородных предметов, в одном из них предметы отличаются по одному признаку (цвету, форме и т.д.). Например, кружочки – с одной стороны красного цвета, а с другой – синего. Педагог выясняет, сколько элементов в каждом множестве (например, по 5), а затем выкладывает из элементов второго множества разные по численности части, отличающиеся по цвету. Всего получится 4 варианта: 1 синий и 4 красных, 2 синих и 3 красных, 3 синих и 2 красных, 4 синих и 1 красный. Затем детям предлагается следующие виды упражнений:

- Выложить (или нарисовать) столько кружочков, сколько не хватает до целого множества.

- Положить в ряд пять квадратов. Под ними положить 2 (3, 4) круга и столько треугольников, чтобы вместе получилось 5 фигур.

- Взять 5 квадратов двух цветов и рассказать, сколько всего квадратов и сколько каждого цвета.

- Разложить 5 пуговиц на 2 тарелочки разными способами, каждый раз проговаривая, сколько пуговиц на каждой тарелочке.

11. Формирование представлений об отношениях между числами (сравнение чисел) (4 – 6 лет)

1 этап (ср.возр.). Детей учат сравнивать смежные числа на основе сравнения 2-х множеств по количеству.

Выясняется, каких предметов больше, сколько каждого вида.

Воспитатель подводит детей к выводу: «Раз мишек больше и мишек 4, то число 4 больше чем 3».

2 этап (ср.возр). Показывается постоянство отношений «больше» и «меньше» между двумя числами, т.е. что 4 всегда больше 3. Для этого в упражнениях меняются качественные признаки предметов и их пространственное расположение.

3 этап (ст.возр.). Показывается, что отношения «больше» и «меньше» относительны, т.е. что число 3<4, но 3>2. Для этого предлагается сравнивать сразу 3 последовательных числа и побуждать детей при ответе обязательно уточнять: данное число «больше» (или «меньше») какого числа.

4 этап (ст.возр). Детей учат сравнивать несмежные числа. Рассуждение проводится на основе свойства транзитивности. Если 3<4<5<6, значит 3<6. При рассуждении следует опираться на наглядно-практический прием «числовая лесенка» (раскладывание предметов в убывающем или возрастающем порядке в параллельные ряды строго один под одним).






Лишние предметы должны быть другого цвета (формы).

Детям показывается, что каждое число больше всех предыдущих, но меньше всех последующих.

Игры и упражнения:

«Живые числа» (построение в правильном порядке), «Что изменилось» (какое число пропущено или поменялось местами и почему), «Продолжай» (с мячом), «Считай наоборот», «Лото», «Назови соседей».


. .

. . . .

. .

.

Во всех этих играх – дети должны дать словесный отсчет.