3.Конспекты лекций Н. Конспекты лекций по дисциплине Теория и методика формирования элементарных математических представлений у детей дошкольного возраста
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
6.2. Предлогическая подготовкаВ программах до 1993 года не ставилась задача предлогической подготовки дошкольников. За рубежом Грин, Лаксон и др. в своих программах ставили задачу развития элементов логического мышления (обучение выполнению операций классификация, систематизация, обобщение и др.). В Беларуси в программе до 1993 года эта задача решалась частично, параллельно при решении других задач. После 1993 г. в новых программах задачи по развитию логического мышления были сформулированы, но в разном объеме в разных программах. Больше всего - в программе «Радуга» (за основу была принята программа Грина и Лаксона). На 2-м месте «Детство», на 3-м «Пралеска». Психологи определили, что элементы логического мышления можно начинать развивать с 4-х лет. Причем сенситивный период для этого заканчивается к 11 годам. Издано множество сборников игр по развитию логического мышления. Инициатор – белорусский ученый А. Столяр. Разработкой содержания и методики предлогической подготовки детей занимались Е.Носова, А.Маркушевич, Соболевский, Скобелев, Фредерик Паппи (бельгиец, книга «Дети и графы»). Педагогами и математиками предложены серии логико-математических или обучающих игр. С помощью их предлагается формировать элементы мышления, учить выполнять логические операции, а также формировать абстрактные математические представления. Разделы:
Задачи на выявление разнообразных способов комбинирования элементов групп.
Построение правильных рассуждений с помощью логических связок и, или, не (отрицания).
Изображение отношений между элементами множеств с помощью стрелок.
Представления о множестве, элементах множества, операциях над множествами.
Задачи на выявление возможности и вероятности наступления того или иного события.
Составление алгоритмов, кодирование информации. Давайте поиграем /Под ред. А.Столяра. 6.3. Докомпьютерная подготовкаПредлагается использовать докомпьютерный (безмашинный, подготовительный) этап в старшем дошкольном возрасте, который включает в себя:
7. Формы организации обучения детей математикеЛитература: /2/, /3/, /4/, /6/, /8/, /9/, /10/, /11/, /17/, /19/, /23/, /26/, /27/, /29/, /30/, /35/, /36, с. 135-142/. В 40-е годы 20 века Леушина А.М. впервые предложила занятия как форму обучения математике в детском саду. Метлина Л.С. в 80-е годы разработала конспекты занятий по математике для всех возрастных групп детей дошкольного возраста. До 90-х годов считалось, что основной формой обучения математике дошкольников является занятие. Для обучения детей математике проводились занятия 1 раз в неделю. Однако надо учитывать, что те математические представления, которые формируются в дошкольном возрасте, носят для детей прикладной характер. Математика нужна детям для ежедневной ориентировки в окружающем мире. Поэтому математика должна быть «растворена» в разнообразных видах деятельности. Под формой обучения математике детей дошкольного возраста будем понимать такую взаимную деятельность педагога и детей, которая способствует процессу познания и направлена на получение новых и использование имеющихся знаний, умений, навыков. В современных программах занятия не являются основной формой обучения, упор делается на различные формы обучения, используемые комплексно. В программе «Пралеска» кроме занятий, которые как правило, называются игровыми комплексами, для обучения математике предлагается использовать ситуации в повседневной жизни, в продуктивных видах деятельности. На занятиях предлагается активно использовать музыку, картины, художественные произведения. Формы обучения математике в Программе «Радуга»:
В программе «Детство» занятия называют учебно-игровой деятельностью. Занятия не считают основным средством работы с дошкольниками. Их количество и продолжительность строго не регламентируется. Воспитатель сам определяет их необходимость, содержание, способ организации, место в режиме дня, исходя из общих дидактических требований. Занятия необходимы для: систематизации, углубления, обобщения личного опыта ребенка в усвоении новых способов действий, в осознании связей и зависимостей, которые скрыты от детей в повседневной жизни и требуют специальных условий и руководства со стороны взрослых. Обучение детей осуществляется в основном в повседневной жизни путем интеграции естественных для дошкольников видов деятельности, главная из которых является игра (общение со взрослыми и сверстниками, экспериментирование, предметная деятельность, изобразительная, художественная, театральная деятельность, труд). Занятия представляют собой комплекс игр-упражнений, объединенных общим героем или темой. В узком смысле слова «занятие» понимается как урок. «Занятие» в широком смысле - есть производное от слова «заниматься». Мы будем использовать термин «занятие» в широком смысле слова. Занятия проводятся в разных формах, ежедневно, во всех возрастных группах. Рассмотрим следующие формы обучения:
-игры с дидактическим материалом, -работа с книжкой (раскрашивание, вырезание, сравнение по величине): книжки типа раскрасок, книжки типа математических тетрадей – «Геометрия для малышей» (авторы Житомирский, Шеврин), «Приключения Кубарика и Томатика или веселая математика» (авторы Левина и Сапгир); -выполнение занимательных упражнений (головоломки, игры с палочками) З.А.Михайлова «Игровые занимательные задачи для дошкольников».
А) планируемые Б) стихийно возникающие ситуации. Задача педагога состоит в том, чтобы увидеть ситуацию и использовать ее.
Авторы: Новикова, Павлова, Ерофеева, Непомнящая Р., Житко И.В., Житомирский (Занимательная математика), Шеврин (Геометрия для малышей, Математическая азбука), Левина, Сапгир (Приключения Кубарика и Томатика, или веселая математика), Моро и др. (Математика в картинках). Индивидуальные тетради используются не на всех, а лишь на некоторых занятиях. Для дошкольников впервые такие теради были разработаны в конце 60-х годов 20 века. Они предназначались в основном для родителей с целью подготовки детей к школе. В 90-х годах такие тетради были разработаны для массовых дошкольных учреждений. Все эти тетради предназначены на один год, их количество должно равняться количеству детей в группе. Все разработанные тетради отличаются друг от друга по яркости, красочности и художественности оформления. В одних тетрадях прямо на странице имеются 2-3 вопроса или задания, в других – предложено большее количество заданий для одной картинки, но записаны они в отдельной части тетради. Для того, чтобы провести занятие по индивидуальной тетради, необходимо составить конспект по одной страничке (картинке). Схема конспекта занятия по индивидуальным тетрадям:
Вводная часть: сюрпризный момент. Основная часть: 1. Объяснение. 2. Вопросы и задания, предполагаемые ответы и действия детей. Все вопросы и задания должны быть сформулированы так, чтобы дети их выполняли в тетрадях, следует исключить хоровые ответы. Формы контроля: воспитатель может пройти по рядам; дети могут поднять цифру или фишку; может быть нашептывание ответа на ушко. Заключительная часть. Преимущества занятий по индивидуальным тетрадям: -способствуют индивидуальному подходу в обучении, -обеспечивают индивидуальный контроль выполнения заданий, -дети могут реализовать желание рисовать в книгах и тетрадях, -сокращается время на подготовку к занятиям, -индивидуальные тетради - яркие, красочные - способствуют привитию интереса к процессу обучения.
Преимущество этой формы: -возможность индивидуального подхода в обучении. -компьютер представляет собой для ребенка интересную игрушку – у детей развивается внимание и интерес к учебе и т.д. Если нарушать правила пользования компьютером, то работа может принести отрицательный эффект. Ребенку 4-6 лет за компьютером можно находиться не более 10 мин., 1-2 раза в неделю (иначе у ребенка нарушается осанка, зрение, психика). Поэтому с помощью компьютера надо решать только те программные задачи, которые в других формах решаются менее эффективно.
- сюжетные: занятия-сказки, занятия-путешествия, игры с элементами драматизаций, сюжетно-ролевые игры с математическим содержанием, праздники на определенную тему. Могут проходить в музыкальном зале, включается музыка, песни, танцы, подбираются костюмы. Путешествовать можно по нескольким сказкам, в экзотические страны, на Северный полюс, в Африку ( в «Д.в.» Шамесова , Непомнящая). Целесообразно придерживаться сюжета сказки, меняя задания в сказках на задания математического характера. Сценарий праздника должен быть написан так, чтобы он не предусматривал репетиций для детей. - бессюжетные ( КВНы, викторины, спортландии), авторы: Ерофеева, Михайлова. Две группы (или группа) детей разделена на подгруппы, задания состоит из нескольких эстафет, должны быть и математические задания. Придумывается система оценок. Существует 2 мнения об организации таких занятий: 1)следует заранее репетировать содержание и ход таких занятий (Непомнящая, Шамесова), 2)такие занятия должны быть для детей сюрпризом. Дети могут использовать песни, стихи, загадки, которые уже знают (Ерофеева, Будько Т.С.)
Тематический комплекс – это совокупность организованных, заранее продуманных разных видов деятельности, взаимосвязанных между собой и объединенных общей темой для совместного решения нескольких дидактических задач из разных разделов программы. Тематический комплекс может длиться как традиционное занятие 15-25 мин., но, как правило, это спаренные 3-4 комплексные занятия, объединенные общей темой. Иногда тематический комплекс может длиться целый день, включать в себя различные режимные моменты. Тематический комплекс разбивается на блоки, в каждом блоке решаются программные задачи из разных разделов, в том числе и по математике, блоки связаны между собой по смыслу. Между блоками необходимо делать перерывы для самостоятельной деятельности детей. Преимущества этой формы обучения: дети познают математические отношения в естественных условиях, процесс обучения идет незаметно для детей, все математические представления запоминаются легче и эффективнее, через определенный промежуток времени у детей легче вызвать воспоминания и ассоциации, т.к. эти представления связаны с определенной темой. Требования к составлению конспекта: следует чередовать физическую и умственную нагрузку, не должно решаться слишком много дидактических задач, целесообразно использовать художественное слово, музыкальные произведения, сюрпризные и игровые моменты, необходимо следить за постоянной сменой расположения детей. Схема конспекта тематического комплекса.
Для всего тематического комплекса должны быть единые вводная и заключительная части. Все блоки должны быть связаны друг с другом по смыслу и объединены темой. В каждом блоке: должна быть своя вводная и заключительная части, должны решаться задачи по математике в комплексе с другими, должны быть четко сформулированы вопросы и задания детям (указаны предполагаемые ответы и действия детей), могут быть дидактические игры, занимательный материал. 8. Содержание и методы работы по математике с детьми 6-летнего возрастаЛитература: /11/, /14/, /15/, /16/, /21/, /22/, /32/, /36, с. 180-196, 221-223/. В программе для 6-тилеток первого класса содержатся те же 5 разделов, что и в программе для детей дошкольного возраста: 1) число и вычисление, 2) знакомство с величиной, 3) геометрические фигуры, 4) ориентировка в пространстве, 5) ориентировка во времени. Центральное место занимает раздел «Число и вычисление» (по значимости и объему). 1) Число и вычисление.Рассмотрим лишь новые программные задачи. 1. Формирование понимания состава числа из 2-х меньших. Рассмотрим состав числа 4. Для этого возьмем красные и синие кружочки. Возможны следующие варианты:     4 синих.     3 синих и 1 красный. Вопросы: Сколько синих? Сколько красных? Сколько вместе? Вывод: 4 это 3 и 1.     2 синих и 2 красных. Вывод: 4 это 2 и 2.     1 синий и 3 красных. Вывод: 4 это 1 и 3.   4 1 2 3    Вставить число так, чтобы дополнить до 4. Вставить число так, чтобы дополнить до 4. 2. Счет группами.Детям показывается, что в качестве единицы счета может быть не только 1, а любое число, можно считать десятками. «Сколько всего цветов в трех букетах по 5 цветочков?», «Сколько купили десятков яиц?» 3. Обучение сложению и вычитанию. Знакомство со знаками « + » и « - ». Сначала проводятся практические действия по объединению и удалению части множества. А затем эти умения используются при решении задач. С действием сложения детей знакомят на основе решения нескольких задач на увеличение множества на один элемент по следующему алгоритму: 1. Выясняется: когда добавили, стало больше или меньше? 2. Вывод: если стало больше, будем говорить «прибавить». 3. Что нужно сделать, чтобы узнать, сколько станет? (прибавить). 4. Действие, когда к одному числу прибавляем другое, называется сложением. 5. Предлагается детям придумать задачу на сложение. Аналогично вводится действие вычитание. Сначала знаки « + »и« - »не используется. Условные знаки вводятся на втором этапе. Показывается, что в математике для записи решения задачи используются специальные знаки. Вместо слова «прибавить» используется знак «+»; вместо «отнять» - знак « - »; вместо «получится» - «=». Предлагаются упражнения для закрепления краткой записи решения задач. 1) Имеются карточки со знаками «+» и «-» , необходимо разложить их в соответствующие примеры: 3 1 = 4, 3 1 = 2. 2) Предлагается соединить стрелкой условие-иллюстрацию с цифровым примером. Нельзя использовать знаки «+» и «-» при чтении условия и при устном решении задачи (можно только при записи). Приемы вычислений. 1. Прием присчитывания (или отсчитывания) по единице. (Основывается на знании состава числа из отдельных единиц). Используя этот прием необходимо второе слагаемое (или вычитаемое) разбить на единицы и последовательно прибавить его к первому слагаемому (или отнять). 5+3=5+(1+1+1)= 6+1+1=7+1=8, 5-3=5-(1+1+1)=4-1-1=3-1=2. 2. Прием основывается на знании состава числа из двух меньших чисел. Состав числа в пределах 10 дети учат наизусть. Например, 4+3=7, т.к. 7 – это 3 и 4. 3. Свойство переместительности (коммутативности): а+b=b+а. 4. Обучение решению арифметических задач. Структура задачи: условие, вопрос, решение, ответ. Виды задач:
Типы задач (в зависимости от выполняемых действий и вопросов):
Этапы и методы обучения решению задач. 1 этап. Детям предлагаются задачи-драматизации с опорой на реальные действия. На этом этапе ведется обучение составлению задач, в которых второе слагаемое или вычитаемое равно 1. Сначала учат детей составлять задачи на сложение, затем на вычитание. Обучение начинается с пояснения структуры задачи, для этого можно использовать провокационные неправильные условия (от имени Незнайки). Дети часто допускают следующие ошибки: а) пропускают вопрос, оставляя условие в виде рассказа, б) в условие не включают числовые данные, в) заменяют задачи загадками с числовыми данными. 2 этап. Детям предлагаются задачи-иллюстрации, в которых нет возможности сводить решение задачи к счёту по представлению. На этом этапе детей учат пояснять выбор арифметических действий. Детям предлагаются задачи с одинаковыми числовыми данными, но на разные действия. Выясняется, почему здесь надо выполнять то или иное действие (добавили, увеличили или отняли, уменьшили). Детей подводят к выводу: если стало больше, то будем прибавлять, а если меньше – будем отнимать. 3 этап. Детей обучают составлению и решению задач, в которых второе слагаемое или вычитаемое больше 1, т.е. обучают приемам присчитывания и отсчитывания. Например, предлагается задача: на озере плавало 4 утки, прилетело еще 3. Дети допускают ошибку - пересчитывают всех уток. Необходимо пояснить: нам известно, сколько было уток, их пересчитывать не надо, надо к тому количеству, что было, прибавить 3, последовательно присчитывая по 1 утке. На 2-м и 3-ем этапах следует добиваться абстрагирования решения от конкретных множеств, т.е. дети подводятся к решению примера. 4 этап. Проводится обучение решению устных задач без наглядного материала. Используются вышеупомянутые приемы вычисления. Педагог должен следить, чтобы дети не заменяли операцию вычисления операцией счета при решении арифметических задач. После получения ответа – необходимо задать вопрос детям «Как ты узнал?» Неправильным будет ответ «Посчитал», правильный ответ «К 5 прибавил 2». 5. Знакомство со знаками «<», «<», «=». Вначале рекомендуется показывать отношения «больше» и «меньше» с помощью направленных стрелок: 1 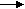 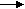 2 3. Затем вводятся общепринятые знаки «>» и «<» . 2 3. Затем вводятся общепринятые знаки «>» и «<» .Детям эти знаки можно пояснить следующим образом: > узенький конец направлен к меньшему числу, а широкий конец к большему числу. < раскрытый клювик направлен к большему числу. Задание: расставить между цифрами знаки «>» и «<». 3 2 1 2 Знаки « >», «<» предназначены для письменной записи отношений «больше» и «меньше». Когда дети устно сравнивают какие-либо числа, слова «больше» и «меньше» не надо заменять знаками. 6. Запись цифр и знаков. До школы учителя не рекомендуют обучать написанию цифр, т.к. могут меняться прописи. В дошкольных учреждениях и в начале 1-го класса рекомендуется записывать примеры с помощью готовых карточек с печатными цифрами и знаками. На первом этапе детей учат писать отдельные элементы цифр и знаков. Затем учат рисовать цифры по пунктирной линии, при этом на рисунке показывается начало движения руки, направление движения, смена направления, конец движения. *  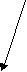 * * * * * начало движения, смена направления, * конец движения. 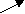 ** - направление движения. ** - направление движения.* Затем детям предлагается прописать цифры по пунктирным линиям, потом просто – в клеточках. Этот алгоритм применяется и к обучению записи других знаков (+, -, <, >, =). 7. Знакомство со 2-м десятком. В качестве наглядности используются счетные палочки по одной и десяток в связке. Сначала детям рассказываем об образовании слов-числительных 2-го десятка. 11 – один-на- дцать – один на 10 (10 сокращенно как «дцать») 12 – это 2 на 10 После этого поясняется значение каждого знака в записи числа. Например, в числе 12 первая цифра обозначает 1 десяток, а вторая – 2 единицы.    1 2 12 1 2 12 2 0 20 Затем детей учат решать примеры. 1-й тип: в качестве слагаемого используется целый десяток, например, 10+3 или 13-10. 2-ой тип: действия происходят в пределах 2-го десятка, нет перехода через границу десятка, например, 15+2 или 17-3. 15+2= (10+5)+2 = 10+(5+2)=10 + 7 = 17. 3-й тип: осуществляется переход через границу 1-го десятка, например 6+7 или 13-8. Для решения этих примеров 2-е слагаемое или вычитаемое надо разбить на 2 удобных числа: одно – чтобы дойти до границы первого десятка, а второе – остаток от числа. 13-8=13-(3+5)= (13-3)-5= 10-5=5. 2) Знакомство с величинойСначала идёт повторение того программного материала, который изучается в старшей группе детского сада: представление о величине, измерение величины с помощью условных мерок. Рассмотрим лишь новые программные задачи. 1. Знакомство с общепринятыми единицами измерения величин (метр, сантиметр, дециметр, литр, килограмм). Алгоритм ознакомления:
2. Формирование понимания функциональной зависимости между единицей измерения и результатом. Необходимо подвести детей к выводу, что чем меньше мерка, тем большее количество раз она поместится в объекте и наоборот. Для этого предлагаются упражнения по измерению одного и того же объекта разными по величине мерками. 3) Геометрические фигурыВ программе 1 класса не предусмотрено повторение имеющихся у детей знаний об объемных геометрических фигурах, а также таких плоских фигурах, как ромб и трапеция. Новые задачи: 1. Рисование плоских геометрических фигур по клеточкам. 2.Знакомство с понятиями «пятиугольник», « многоугольник». Методика ознакомления с обобщающим понятием «многоугольник» аналогична методике обучения обобщению фигур по форме, используемой в дошкольном возрасте. 3.Ознакомление с понятиями: отрезок, ломаная (звенья ломаной), треугольник, квадрат, периметр. 4) Ориентировка в пространствеНовых задач в программе нет. Закрепляются умения ориентироваться в двухмерном пространстве. 5) Ориентировка во времени1. Ознакомление с циферблатом часов, формирование умения определять время по часам. Задача решается в процессе повторения цифр. Детей учат ориентироваться сначала с точностью до 1 часа, затем - до ½ часа, и, наконец, до ¼ часа. Час рассматривается как целый круг. Если стрелка прошла четверть круга, то прошло четверть часа. Если у детей имеется интерес, то, начиная со старшего дошкольного возраста, можно их учить определять время более точно (например, используя развивающую игру «Часы» Б. Никитина). К этому времени дети должны уметь считать в пределах 60. На модели Никитина имеется 2 циферблата, по 1 шкале определяется, сколько часов, а по второй - сколько минут. 2. Ознакомление с календарем, как системой мер времени. Детей знакомят с разными видами и моделями календаря, учат запоминать последовательность месяцев. Предлагаются задачи, в которых единицей счета являются час, сутки, неделя, месяц, год. 3. Развитие чувства времени Детей необходимо учить определять время без часов. Для этого их знакомят с длительностью интервалов 1, 3, 5, 10 минут. Детям предлагается за определенное время выполнить какие-либо действия (выложить из палочек узор, нарисовать орнамент, одеться и т.д.). При выполнении деятельности детям предоставляется право следить за течением времени по нескольким видам часов (механическим, песочным, электронным). Чтобы показать относительность восприятия времени, надо предложить детям за один и тот же промежуток времени выполнить интересную и неинтересную работу. 6) Кроме формирования математических представлений, программой 1 класса предусмотрена предлогическая подготовка детей, которая включает в себя формирование представлений о множестве, элементах множества, операциях над множествами, о свойствах предметов, формирование умений называть и отрицать свойства объектов. 9. Преемственность в обучении математике в начальной школе и дошкольных учрежденияхЛитература: /14/, /16/, /26/, /36/. Преемственность заключается в установлении взаимосвязи задач, содержания, форм и методов обучения детей в детском саду и школе. С одной стороны необходим учет в дошкольном учреждении всех требований школы, а с другой – опора на достигнутый уровень развития, знания и умения детей. Преемственность в содержании обучения заключается в следующем: - в основе обеих программ лежит теория множеств, - еще в детском саду дети овладевают математическим языком, что является опорой для будущего обучения, - в детском саду у детей формируются представления о некоторых математических понятиях, в 1 классе вводятся отдельные понятия, содержание знаний поднимается на новую ступень, осмысливается с теоретических позиций, - в программе 1 класса продолжается изучение материала в рамках тех же 5 разделов, что и в детском саду. Однако, в содержании программ имеет место факт нарушения преемственности. Так, например, в разделе «Геометрические фигуры» полученные детьми в старшем дошкольном возрасте представления о некоторых плоских (ромб, трапеция) и объемных фигурах даже не повторяются. В разделе «Ориентировка в пространстве» нет продолжения решения такой сложной программной задачи, как трансформация 3-хмерного пространства в 2-хмерное. Преемственность детского сада и школы проявляется также и в методах обучения. По-прежнему основное место занимают практические методы, ведущим из которых является игра. Первоклассникам дается больше самостоятельности при выполнении упражнений, все чаще используются продуктивные методы. В качестве наглядного материала педагог уже использует не игрушки, не картинки, а более абстрактную наглядность (счетные палочки, фигуры). Больше требований предъявляется к словесным методам, детей учат рассуждать. В первом классе, как и в дошкольном возрасте, детей учат рассуждать по индукции (у синего квадрата 4 равных угла и 4 равных стороны, и у красного квадрата 4 равных угла и 4 равных стороны, значит у всех квадратов 4 равных угла и 4 равных стороны). Методы дедукции также используются в элементарной форме для доказательства некоторых умозаключений, необходимо детям чаще задавать вопросы: почему? Как ты узнал? Объясни? Использование этих методов позволяет развивать мышление детей и обеспечивает преемственность между математической подготовкой детей в детском саду и 1 классе. Преемственность детского сада и школы существует также и в формах обучения: В 1-м классе уроки по математике проводятся в игровой форме по 30 минут 4 раза в неделю, домашних заданий нет. Чтобы обеспечить преемственность в формах обучения, воспитатель обязан провести в старшей группе несколько занятий, аналогичных школьным урокам (длительность до 25 минут, когда дети сидят за столами по 2, учатся поднимать руку, если желают ответить, учатся удерживать внимание, выполняя задание воспитателя). 10. Из истории развития методики формирования математических представлений у детей дошкольного возрастаЛитература: /14, с. 29-53/, /36, с. 13-27/. Тихеева Е., Морозова М. Счет в жизни маленьких детей. - Л., Изд. музея «Дошк. жизнь ребенка», Современный детский сад /Сост. Тихеева Е. и др. – Л., Государственное издательство. – 1920. Формированию математических представлений у детей способствовали: народные игры, наблюдения за трудом взрослых, помощь взрослым, устное народное творчество. В 16-19 веках педагоги под влиянием практики пришли к выводу о необходимости специальной подготовки детей 4-7 лет к усвоению математики. Ими высказаны предложения о содержании и методах обучения детей в семье. Специальных пособий по математической подготовке они не разрабатывали, а включали свои идеи в книги по воспитанию и обучению. В 16 веке И.Федоров опубликовал «Букварь», в котором был раздел посвященный началам математики. Впервые была выдвинута мысль об обучении счету в процессе специальных упражнений. Я.А.Каменский – чешский педагог (17в.) - в произведении «Материнская школа» предлагал обучать детей 4-6 лет считать в пределах 20, сравнивать числа, применять меры измерения и знакомить детей с геометрическими фигурами. И.Г.Песталоцци – швейцарский педагог (18в.) - в произведении «Как Гертруда учит своих детей» предлагал учить счету конкретных предметов, учить осознавать арифметические действия и определять время. Большое внимание уделял наглядности. Разработал систему обучения счету, в основе которой лежали число, форма и слово. В России в 18 в. Л.Ф.Магницкий издал первую печатную русскую книгу «Арифметика». Предлагал обучать детей нумерации, выполнять арифметические действия, решать примеры и задачи без пояснения. К.Д.Ушинский (19в.) предлагал обучать детей-дошкольников счёту отдельных предметов и групп, счёту десятками; выполнять арифметические действия. Л.Толстой (в 19 веке) выпустил «Азбуку», в которой в разделе «Счет» рекомендовал учить детей считать вперед и назад в пределах 100 и знакомить с цифрами. Обучение предлагал осуществлять через игру. Ф.Фребель в нач. 19 века создал пособие «Дары», в котором предлагал обучение счету через усвоение ряда чисел, ознакомление с геометрическими формами, величиной, ориентировкой в пространстве с помощью специальных дидактических пособий «Дары» (строительные детали). М. Монтессори (конец 19 - нач.20 вв.) в книге «Дом ребенка» предложила специальный дидактический материал, с помощью которого формировалось представление о числах в пределах 1000, о цифрах, геометрических фигурах, величинах. Монографический метод Идея монографического метода принадлежит немецкому педагогу А.В.Грубе (19в., «Руководство к счислению в элементарной школе…»). Его последователи: - немецкий педагог В.А. Лай (к. 19 – н. 20в.) в «Руководстве к первоначальному обучению арифметике…», - В.А. Евтушевский (к. 19в.) «Методика арифметики», - Д.Л. Волковский (в 1914 г.) этот метод перенес в детский сад, издав книгу «Детский мир в числах». В переводе монографический метод означает «описание числа». Суть метода состоит в следующем: т.к. дети способны воспроизвести группу предметов в пределах 100, то каждое число изучается путём рассматривания соответствующего количества точек (или чёрточек), сравнивается с другими числами (из каких чисел оно состоит, сколько раз в него вмещается то или иное число, на сколько оно больше или меньше других чисел). Арифметическим действиям детей не обучают, т.к. считается, что они сами вытекают из знания детьми состава чисел. Весь изучаемый материал располагался по числам и изучались все действия для каждого числа. По сравнению с Грубе, Лай использовал специальные числовые фигуры, т.е. каждое число он изображал в удобной для восприятия форме, и считал, это если дети легко воспроизводят эти числовые фигуры, то они запомнили соответствующее число. Евтушевский этот метод упростил, предлагая вести обучение в пределах 20 , а не 100. Волковский рекомендовал этот метод для детей до школы, предлагая вести обучение в пределах 10. В современной методике ознакомления с числами использованы положительные стороны монографического метода: воспроизведение групп предметов, применение числовых фигур и счётных карточек, изучение состав числа. Вычислительный метод Вычислительный метод по-другому называется «метод изучения действий», который предполагает научить детей не только вычислять, но и понимать смысл этих действий. Детей обучали считать конкретные множества, усваивать нумерацию, а затем переводили к изучению арифметических действий и вычислительных приёмов. Т. е. обучение шло от практических действий с множествами к усвоению операции счёта и пониманию числа, а затем - усвоению понятия натурального ряда чисел и пониманию построения десятичной системы счисления. Обучение и пояснение велось по десятичным концентрам (сначала в пределах первого десятка, затем по аналогии – в пределах 20 и т.д.). Этот метод предложили в конце 19 в.: П.С. Гурьев в России, А. Дистервег в Германии («Руководство к преподаванию арифметики малолетним детям»). Их последователи в России: А.И. Гольденберг, С.И. Шохор-Троцкий, Ф.И. Егоров. В современной методике ознакомления с числами использованы положительные стороны вычислительного метода: число как результат счёта, образование чисел на основе сравнения двух совокупностей и установления между ними взаимно однозначного соответствия, увеличение или уменьшение одного из них на 1, освоение действий сложения и вычитания. Обучение математике в первых дошкольных учреждениях в начале 20 века В.А.Кемниц («Математика в детском саду», 1912 г.) изложила содержание и методы математического материала в форме бесед, игр, упражнений. В книге присутствуют все разделы современной программы. Л.К.Шлегер («Особенности работы с детьми-семилетками», 1925 г.) предлагала давать детям не готовые знания, а развивать у них способность черпать эти знания из окружающей жизни самостоятельно. Считала, что воспитатель должен организовать жизнь детей, вызывать желание расширять свой опыт, углублять имеющиеся знания, что обучение должно осуществляться в процессе повседневной жизни игр детей. Она отрицала необходимость программы и специально-организованного обучения. Ф.Н.Блехер создала первую в СССР программу и методическое пособие для воспитателей по дошкольной математике («Математика в детском саду и нулевой группе», 1934 г.). Считала, что дети должны воспринимать количество в пределах 10 без счета («схватывать числа»). Не подчеркивала отличие между конкретным множеством и отвлечённым понятием числа. Л.В.Глаголева – в основе ее методики лежал монографический метод. До 40-х годов детей обучали счёту по методике Глаголевой. В её пособиях раскрыты содержание, методы и приёмы формирования у детей первоначальных представлений о числах, величинах и их измерении, делении целого на равные части. Е.И. Тихеева об обучении математике дошкольников По мнению Е.И.Тихеевой развитие математических представлений у ребенка должно происходить из его практических потребностей в нормальной, естественной жизни. Однако, роль воспитателя при таком развитии очень велика и ответственна (вопреки утверждениям критиков Тихеевой). Действительно, - «взрослые должны обставить жизнь детей так, чтобы каждая способность каждого из них развивалась интенсивно и беспрепятственно, чтобы все их духовные запросы находили удовлетворение», - «взрослые должны быть незаметными пособниками и руководителями детей», - взрослые должны вводить в жизнь ребенка развивающий материал, - взрослые должны следить за тем, на какой ступени развития находится каждый из детей, каков его запас сведений и представлений. - взрослые должны использовать все возможности выдвигаемые жизнью для ФЭМП и в порядке простого непринужденного разговора использовать каждый из них соответственно той или иной цели, - в играх-занятиях на первоначальном этапе взрослые должны сами принимать участие. При этом, чем больше взрослые вложат в игры жизни, подвижности, разнообразия, тем с большим интересом дети будут к ним относиться, тем интенсивнее будут развиваться. Однако взрослый должен предлагать ребенку задачу-игру «лишь тогда, когда убедится, что соответствующее представление уже усвоено ребенком путем наблюдения и действенного участия в жизни. Воспитателю (да и всем взрослым) отводится очень сложная роль и при этом очень необходимая: без воспитателя ребенок не сможет развиваться. Тихеева утверждала: «Ребенок, играя, трудясь, живя и пользуясь самостоятельно каждым удобным случаем жизни, нами взрослыми, надлежащим образом обставленной, научится сам всему, чему ему надлежит в первые годы научиться. Усвоит то или другое познание именно тогда, когда его духовные интересы этого потребуют, и усвоит в том именно виде, в котором сама жизнь это знание перед ним представит. Воспитателю надо быть осторожным и последовательным в своем методическом отношении к каждому из малышей, надо считаться с той ступенью развития, на которой каждый из них находится, спрашивать с каждого по силе его, но развитие этих детей будет шириться и углубляться помимо вас, не считаясь лишь с вашим личным воздействием. Младшие дети наблюдают игры, занятия своих старших товарищей и усваивают невольно и незаметно так много, что принуждают вас перескакивать сразу через несколько ступеней той лестницы методических приемов, по которой вы имеете твердое намерение шествовать последовательно и планомерно. При таких условиях развитие каждого ребенка совершается строго индивидуально, соответственно интересам и духовным запросам каждого из них. Коллективные уроки стремятся к тому, чтобы все дети сразу и в одно и то же время усвоили то, что им на этих уроках преподносят: сегодня все познакомились с 1, через неделю узнают, как записать число 2 и т.п. В детском саду этого не должно быть. Познания детей будут различны, степень их развития не одинакова, но это должно не пугать, а радовать сознательного воспитателя. «К душе навязываемое знание не пристанет», сказал Платон уже 4 века до н.э. Коллективные же уроки в применении с маленьким детям неизбежно навязывают знание большинству из них. Единственно правильный путь тот, когда душа ребенка сама воспринимает то, до чего она доросла и чего она сама просит. Вклад А.М.Леушиной в разработку содержания, форм и методов формирования математических представлений у детей дошкольного возраста Начиная с 40-х годов 20 века благодаря исследованиям А.М.Леушиной методика формирования математических представлений у детей дошкольного возраста получила научное и теоретическое обоснование. Ею были раскрыты психолого-педагогические особенности восприятия математических представлений у детей раннего и дошкольного возраста. А.М.Леушиной были введены занятия как основная форма обучения детей математике в детском саду. Ею были разработаны программа, содержание и методы работы с детьми 3-,4-,5- и 6-летнего возраста. Методическая концепция формирования математических представлений у детей дошкольного возраста А.М.Леушиной заключается в следующем: Сначала следует дочисловой период обучения, детей учат выполнять различные операции над множествами. От нерасчленённого восприятия множеств предметов детей необходимо переводить к выявлению его отдельных элементов путём их попарного сопоставления. Затем следует обучение детей счёту, которое базируется на сравнении двух групп предметов. Дети знакомятся с числом как результатом счёта, затем как характеристикой численности конкретной группы предметов. Затем усваивается последовательность чисел и отношения между ними. Представление о числе обобщается на основе сравнения нескольких групп предметов по признаку количества независимо от других признаков. В 60-70 годы А.М.Леушиной и её последователями были разработаны содержание и методы формирования у детей пространственных и временных представлений, обучения измерению величины объектов. Результаты научных исследований А.М.Леушиной отражены в её докторской диссертации «Подготовка детей к усвоению арифметического материала в школе» (1956), многочисленных учебных и методических пособиях, например: «Занятия по счету в детском саду» (1963), «Формирование элементарных математических представлений у детей дошкольного возраста» (1974). |
