Лекции по прочности двигателей. Лек_Проч_РД!. Конструкционная прочность элементов ла

• Название: Конструкционная прочность элементов ла
• Анкор: Лекции по прочности двигателей
• Дата: 28.06.2022
• Размер: 1.21 Mb.
• Имя файла: Лек_Проч_РД!.doc
• Тип: Анализ; #618558
• страница: 6 из 7

2.5 Частные случаи напряжённого состояния. Инварианты тензора напряжений.

Если около данной точки мысленно вырезать несколько элементарных параллелепипедов, грани которых различным образом ориентированы в пространстве, то, очевидно, компоненты напряжений на их гранях будут различны. Однако, также очевидно, что независимо от ориентации параллелепипедов в пространстве подстановка значений их компонент напряжений в уравнение (5.8) должна дать в итоге одни и те же значения главных напряжений, т. к. главные напряжения в данной точке всегда объективно существуют и их величины не зависят от метода их определения, то есть они инвариантны по отношению к преобразованию координатной системы.

Следовательно, корни кубического уравнения (5.8) не должны зависеть от системы координат, а значит и коэффициенты этого уравнения также не зависят от выбора координатной системы. Другими словами, коэффициенты уравнения (2.15) - инварианты преобразования координат.

Перепишем уравнение (2.15) в виде:



где I₁, I₂ и I₃ - соответственно первый, второй и третий инварианты тензора напряжений: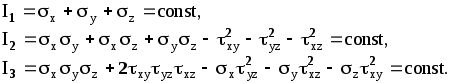



Заметим, что второй (или квадратичный) инвариант представляет формально сумму миноров тензора напряжений как определителя, если произвести его разложение по главной диагонали:



а третий инвариант (кубический) - не что иное, как развёрнутый в строку определитель, составленный из компонент тензора напряжений: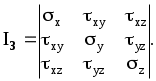



В теории напряжений данные инварианты рассматриваются как основные характеристики напряжённого состояния в точке, а компоненты тензора напряжений - вспомогательные характеристики.

Заметим, что в общем случае уравнение (2.15) имеет громоздкое аналитическое решение (формула Кардано) и его следует решать численно, например, методом касательных.

В частных случаях плоского и одномерного напряжённых состояний аналитическое решение имеется.

Рассмотрим плоское пространство, исключив, например, ось Z и, как следствие, обнулив в тензоре напряжений компоненты, содержащие индексы z: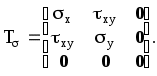



В этом случае инварианты тензора запишутся так:







а основное уравнение имеет вид:

откуда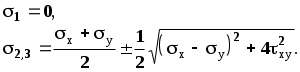

Полученные формулы совпадают с соответствующими формулами для плоского напряжённого состояния в курсе «Сопротивление материалов».

ЛЕКЦИЯ_5

3. Основы теории деформаций.

3.1 Основная задача теории деформаций. Фундаментальное соотношение теории деформаций.
Изменение формы тела (его деформация) связана с перемещением точек этого тела.

Рассмотрим два состояния тела - начальное (до деформации) и деформированное.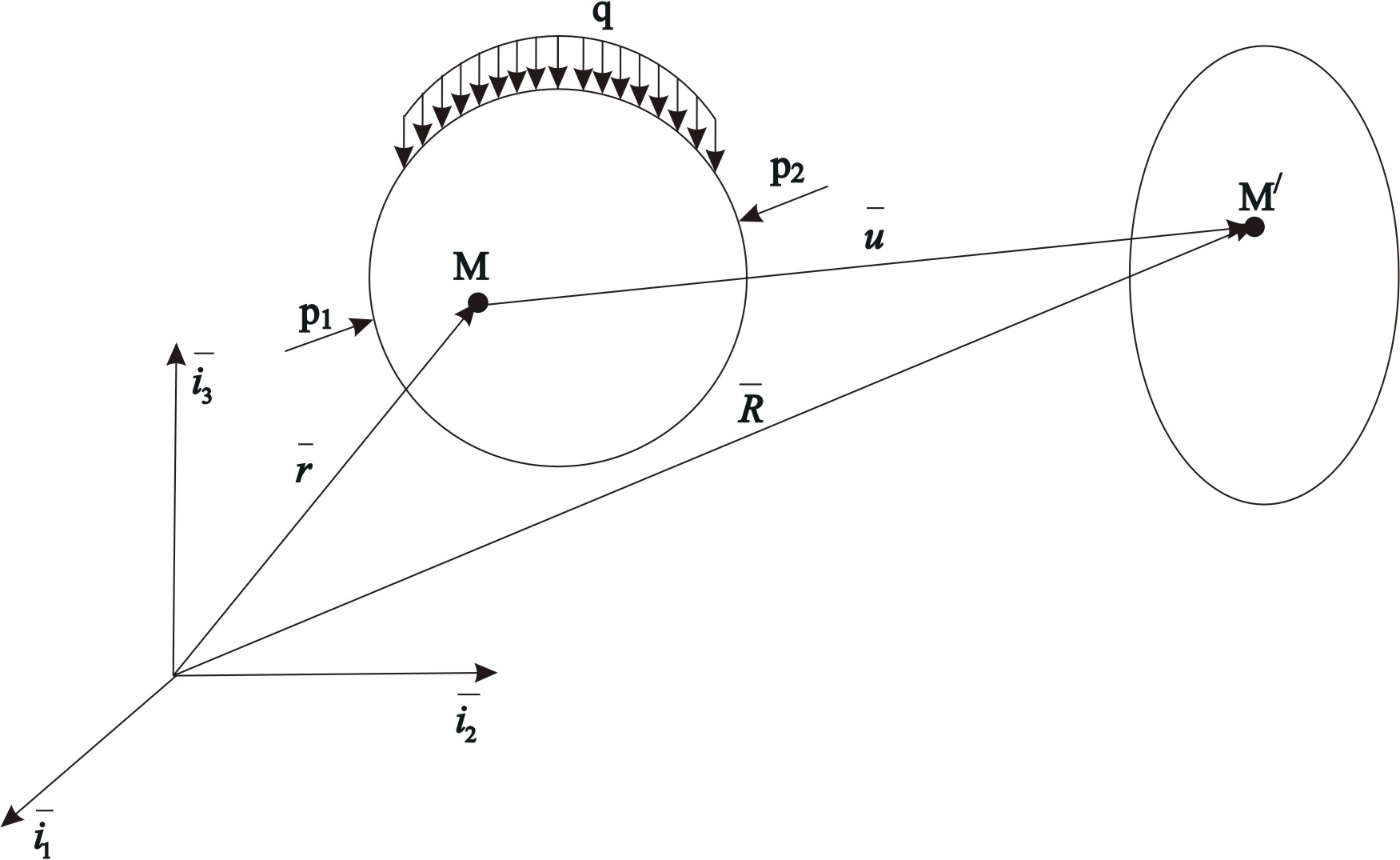



Рис.1.

Введем некоторую систему координат (декартовую) с единичными векторами .

Положение произвольной точки М определяется радиус – вектором .

В механике деформируемого твердого тела (МДТТ) принято обозначать оси координат не , а , или просто цифрами .

Это связано с правилом суммирования по повторяющемуся индексу.

В дальнейшем будем считать, что если в одном и том же выражении один и тот же индекс повторяется дважды, то по этому индексу предполагается суммирование.

Пояснение:

.

Положение той же произвольной точки после деформации тела определяется радиус – вектором . Все параметры, характеризующие состояние тела после деформации будем помечать со знаком «штрих».



Перемещение точки М можно определить по формуле:

.

Перемещение произвольной точки ( ) является функцией трех координат: перемещения, температуры и времени:

.

Перемещение произвольной точки можно представить в следующем виде:

.

Функции это основные неизвестные, которые необходимо вычислить для определения деформированного состояния тела.

;

;

.

Замечание: в МДТТ принята точка зрения Лагранжа, в соответствии с которой основными аргументами являются координаты точек в начальном состоянии. В газовой динамике, аэродинамике принята точка зрения Эйлера, в соответствии с которой основными аргументами являются пространственные координаты.

Основная задача теории деформаций

Основная задача теории деформаций – это научиться вычислять удлинение волокон и сдвиг между ними через функции перемещений или .

Первая подзадача – указать формулу или способ для вычисления длины волокна в деформированном состоянии.

Рассмотрим два состояния тела: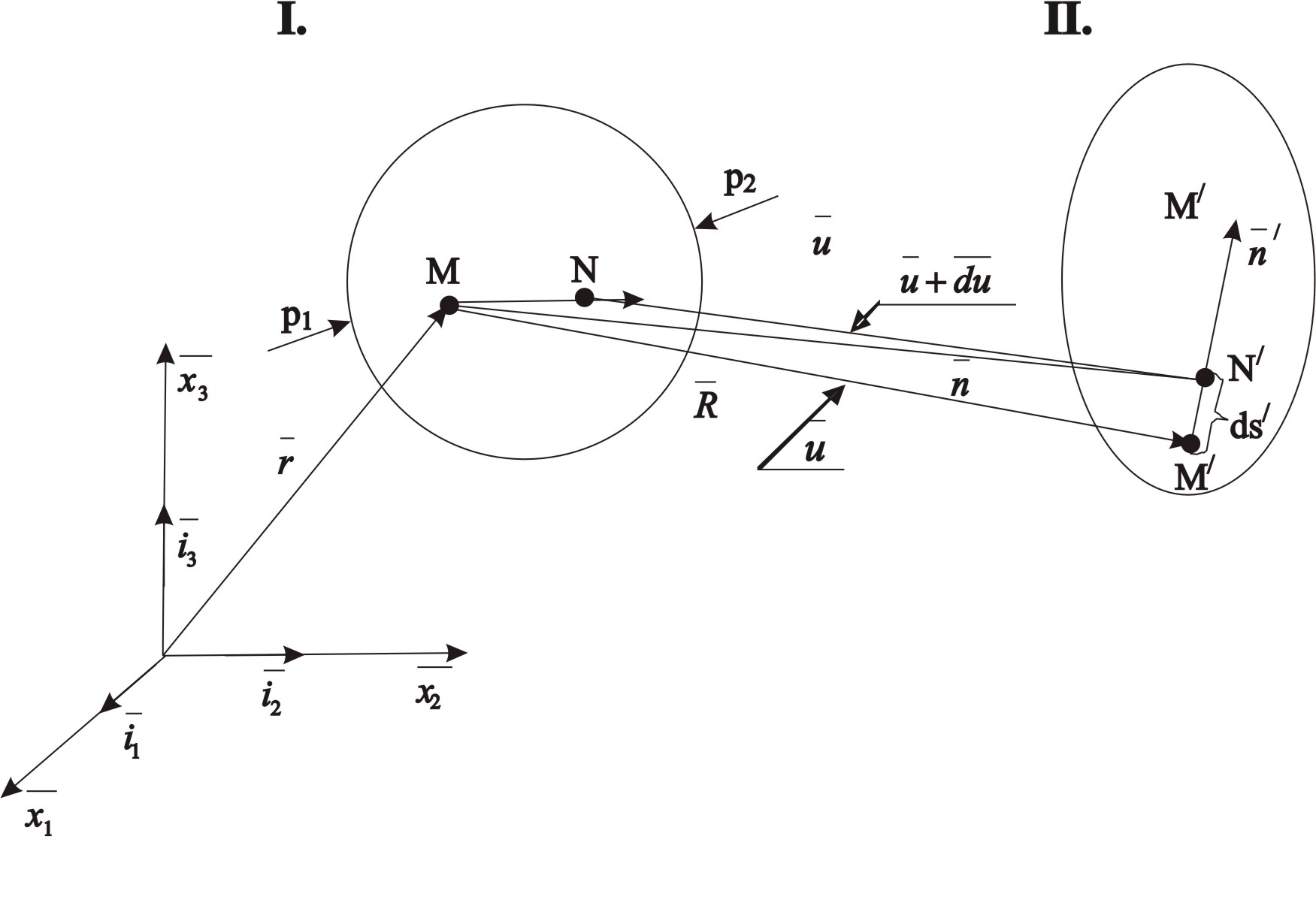


Рис.2.

Единичные векторы образуют правую тройку векторов. Из произвольной точки М направим бесконечно малое волокно в произвольном направлении. Обозначим N конечную точку волокна. Длину бесконечно малого волокна MN обозначим ds. Направление волокна будем всегда характеризовать единичным вектором, который равен:

;

.

Рассмотрим векторный четырехугольник . На основании векторного равенства можно записать:

;

;

.

Разделим все на ds:

.

Из курса сопротивления материалов известно, что отношение конечной длины деформированного волокна к начальной его длине называется абсолютным удлинением волокна. Абсолютное удлинение волокна можно найти по формуле:



где n – показывает направление волокна.

Относительное удлинение волокна можно вычислить по следующей зависимости:

.

В случае одномерного растяжения, относительное удлинение совпадает с деформацией волокна с направлением :

.

Полученное соотношение можно трактовать как одну из форм записи фундаментального соотношения теории деформации.

Проведем ряд вычислений:

;

;

;

.

Правило: в механике принято обозначать производную по направлению с помощью символа « , ».

Например:

;

;

.

В соответствии с этим правилом перепишем выше рассмотренные зависимости в следующем виде:

;

;

;

;

;

. (Ф)

Это еще одна запись фундаментального соотношения теории деформации:

.

В последнем выражении правило суммирования индексов совпадает с предыдущим.

Если полярно перемножить два последних вектора можно определить модуль (квадрат модуля) данного вектора (длину).



Вывод: используя фундаментальное соотношение теории деформации (Ф) можно найти удлинение произвольного волокна, задаваясь его направлением ( 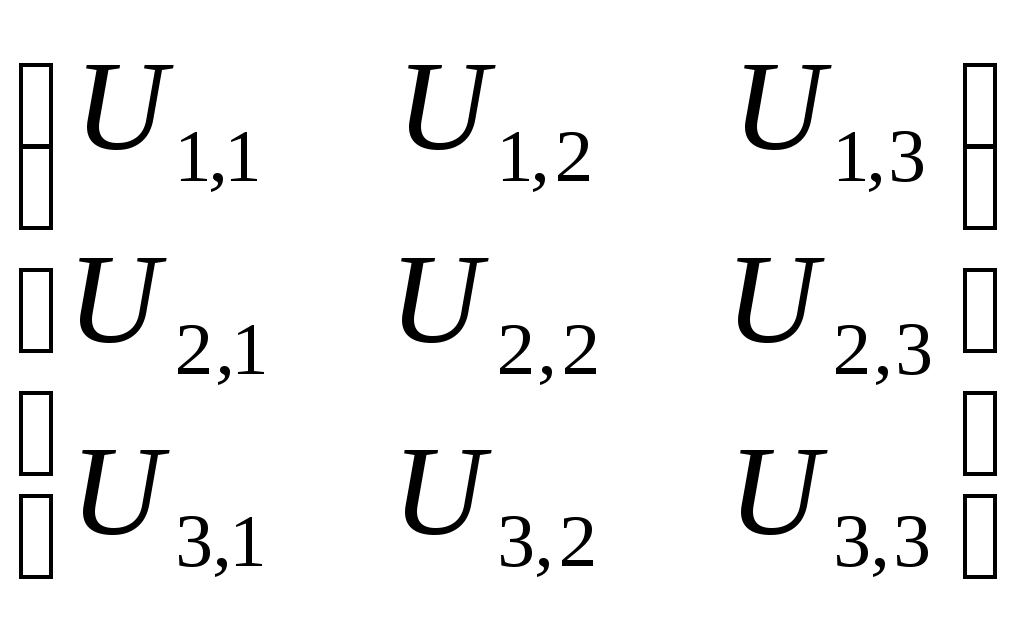) и зная девять производных . Данные производные от функции перемещения удобно записывать в виде матрицы:

.

ЛЕКЦИЯ_6

3.2. Тензор деформаций. Компоненты деформаций и их физический смысл.
На прошлой лекции было показано, что для решения основной задачи МДТТ необходимо научиться вычислять компоненты матрицы производных от перемещений, размерностью 3×3. Данная матрица содержит не девять, а только шесть неизвестных функций, т.к. некоторые компоненты одинаковы.

Докажем это:

;

;



.

При преобразовании данного выражения мы заменяем индекс s на q,p, т.к. происходит суммирование, в результат чего индекс можно заменить на любую букву.

;

,

где – компоненты деформаций Грина.

В случае если деформации тела малы, используются соотношения Коши для вычисления деформаций:

.

Здесь и в дальнейшем при рассмотрении малых величин будем пренебрегать величинами высшего порядка малости, а именно произведением двух малых величин по сравнению с самой малой величиной. Таким образом, для вычисления нового удлинения и нового направления произвольного волокна необходимо знать 6 чисел, представляющих собой определенные комбинации от функций производных перемещений по координатам. Эти шесть чисел удобно представить в виде матрицы: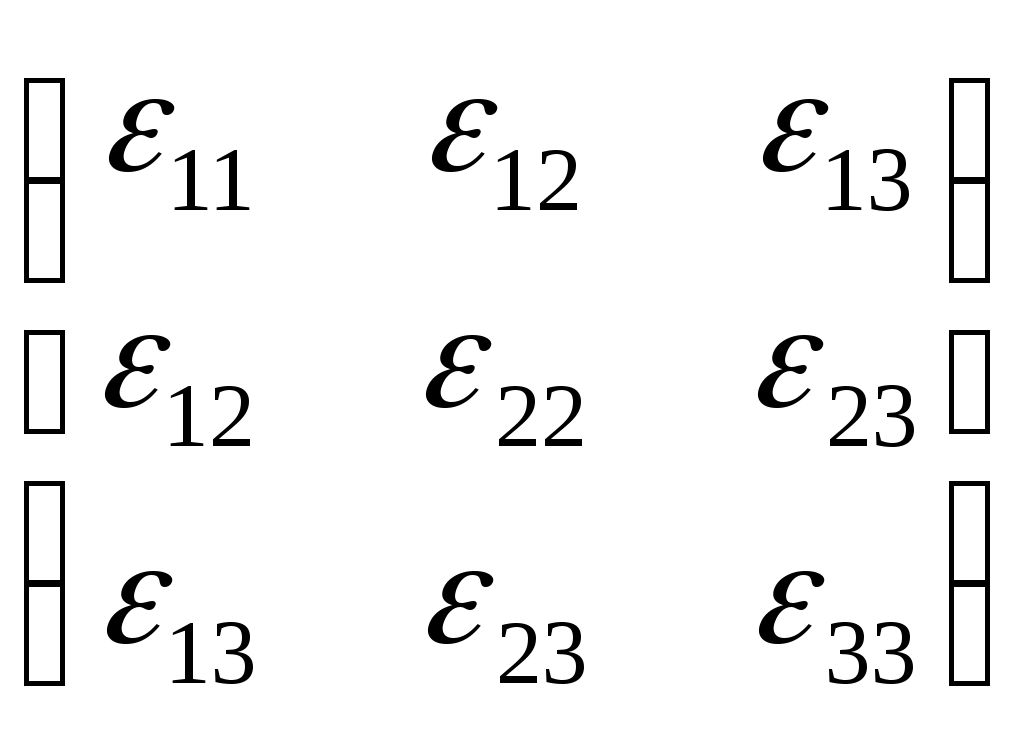

.

Так как 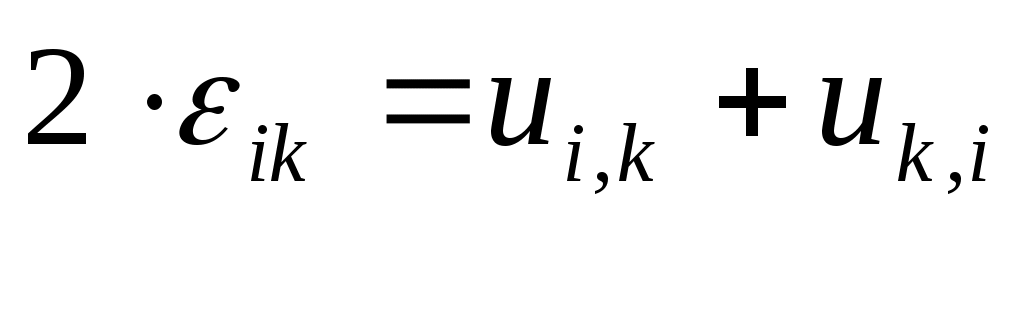– компоненты данной матрицы, имеющие одинаковые индексы, равны.

Компоненты данной матрицы имеют явный физический смысл и связаны друг с другом. При переходе от одной системы координат к другой определенная комбинация компонентов этой матрицы, называется инвариантами тензора деформаций, не меняет своего значения. А саму эту матрицу принято называть тензором деформаций. Зная все шесть компонентов тензора деформаций можно однозначно описать деформацию окрестности произвольной точки тела.

Диагональные элементы представляют собой относительное удлинение соответствующих координатных волокон (почти!). Элементы со смешанными индексами – это сдвиг (изменение угла) между координатами волокон.

Рассмотрим пример: рассмотрим волокно, направленное вдоль координатного направления 1.

т.к. ;

;

;

;

.

Мы не учитываем величину , т. к. малыми величинами пренебрегаем.

.

Для доказательства второй половины утверждения достаточно выписать фундаментальное соотношение для этих волокон и перемножить их.

Т.о., компоненты тензора деформаций имеют явный физический смысл. Более полное и строгое обоснование тензорности полученных величин можно найти в литературе.
3.3 Главные оси и главные деформации.

В каждой точке деформируемого тела существуют три особенных направления, называемых главными. Если систему координат совместить с данными направлениями, то в процессе деформации тела координатные волокна изменят свою длину, но углы между ними останутся прямыми. Тензор деформаций будет иметь такой вид: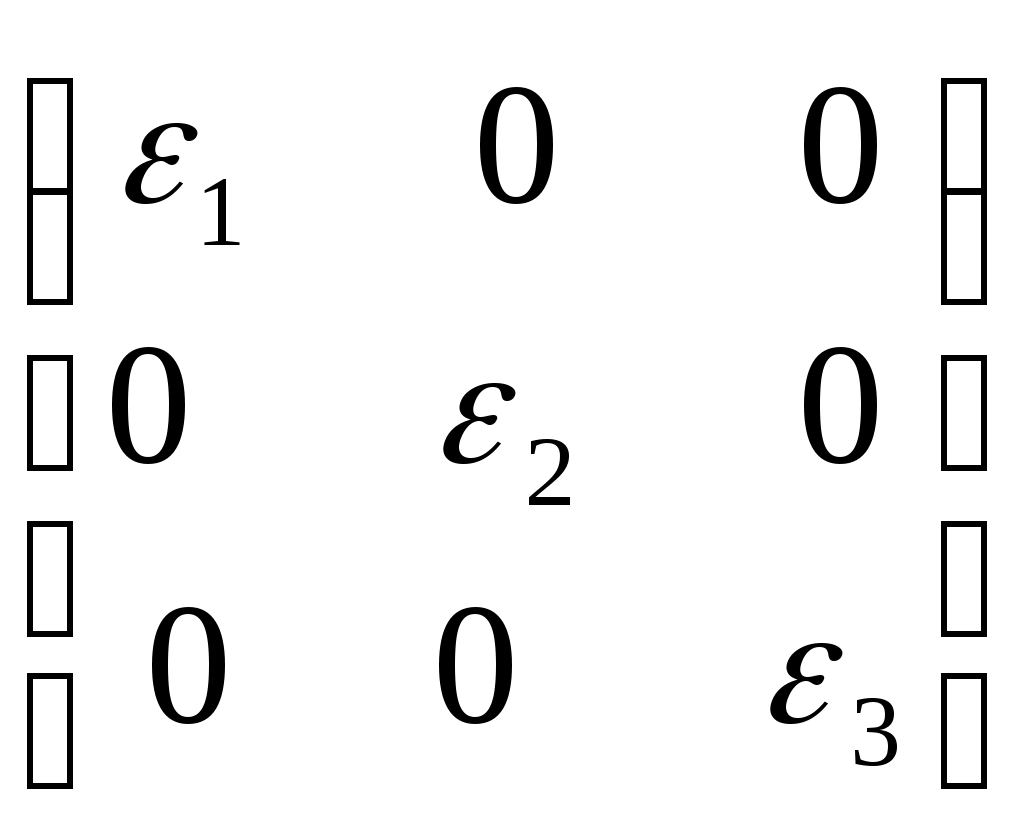

.

Инварианты тензора деформаций вводятся по аналогии с теорией напряжений.

ЛЕКЦИЯ_7
4. Постановка задачи МДТТ в перемещениях
Основная задача МДТТ сводится к следующему – зная систему внешних сил, действующих на деформированное твердое тело, необходимо определить пятнадцать неизвестных пока величин, характеризуя напряженно деформированное состояние (НДС) этого тела:

;

;

.

Решение данной задачи осуществляется по средствам использования трех блоков: геометрического, физического, механического.

Геометрический блок:

.

Физический блок:

.

Механический блок: законы движения

4.1Обобщенный закон Гука

Для большинства материалов компоненты тензора напряжений и тензора деформаций связаны между собой линейной связью:

;

;

;

;

;

,

где G – модуль сдвига.

Относительно деформаций это зависимости можно переписать в виде:

;

;

;

;

;

.

Данные соотношения принято называть обобщенным законом Гука.
4.2 Уравнения движения (механический блок)
Необходимо в реальном теле найти такие объекты, моделируя состояние которых можно использовать законы классической механики Ньютона. Это бесконечно малые элементы объема. Необходимо выделить в реальном теле объем, ограниченный поверхностями, параллельными координатным, т.о. чтобы грани этого объема были бесконечно малыми величинами. Тогда напряжения на каждой грани можно считать постоянными. Применительно к декартовой системе координат будем иметь: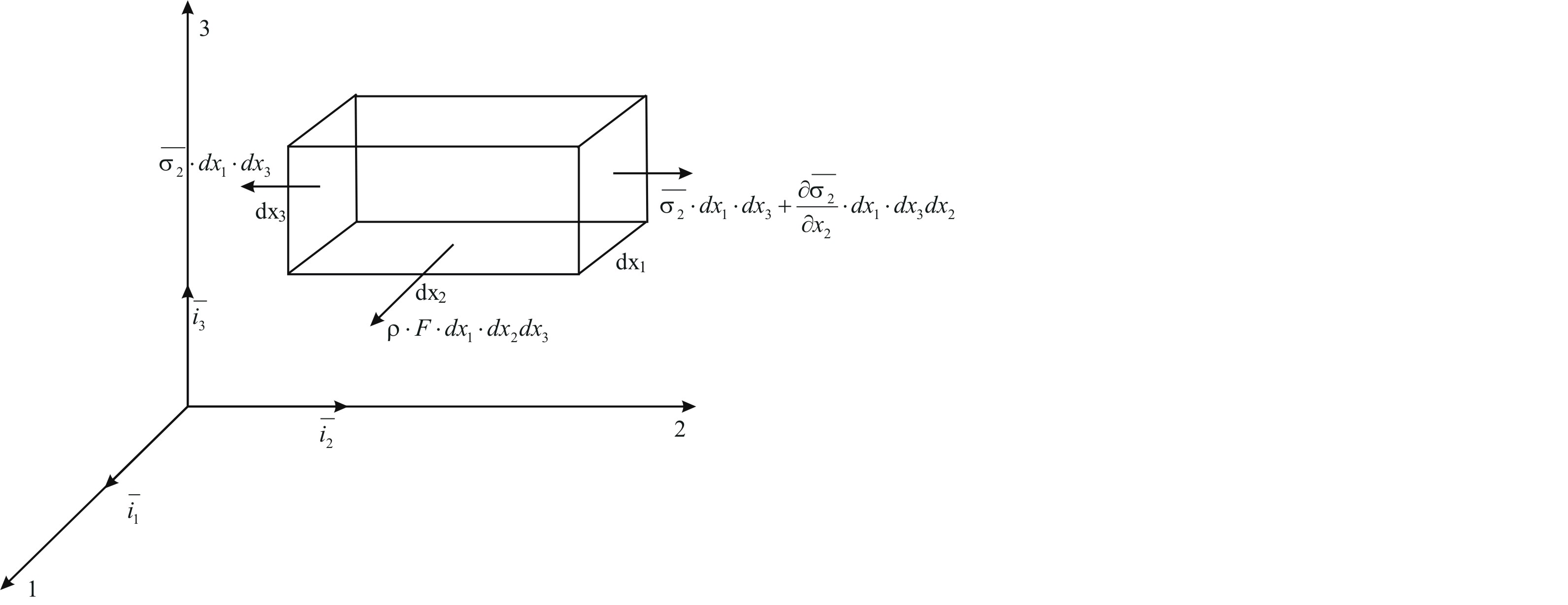



Рис.6.

т.к. нормаль совпадает с осью 2.

;

.

Аналогично можно поступить с остальными гранями.

По аналогии с силами, действующими на грани, нормаль к которым направлена вдоль оси 2, можно определить силы на оставшихся гранях.

В общем виде эти силы будут выглядеть так:

Суммируя силы на противоположенных гранях и, учитывая, что они направлены в противоположенные стороны, получим:

.

Поделив на величину, запишем уравнение движения в более компактном виде:

;

.

Т.о. получено уравнение движения малого бесконечного объема в векторной форме.
Определение запасов прочности. Предельное состояние конструкций.
ЛЕКЦИЯ_8

5. Предельное состояние конструкций
5.1. ПОНЯТИЕ О ПРЕДЕЛЬНОМ СОСТОЯНИИ
В практике эксплуатации и испытания прочности конструкций (или элементов конструкций) часто приходится выяснять, какова величина нагрузки, которую способна выдержать конструкция до полного исчерпания ее несущей способности.

Опыт показывает, что для конструкции из пластичного материала при неравномерном распределении напряжений по сечению, достижение в одной точке разрушающего напряжения s_разр еще не вызывает разрушения конструкции в целом. Хотя после начала тянучести конструкция получает небольшие остаточные деформации, ее несущая способность не исчерпана и она может служить целям передачи все увеличивающейся нагрузки до тех пор, пока тянучесть не охватит всего опасного сечения. Одним из важных примеров является случай, когда наибольшие напряжения относятся к категории местных напряжений, быстро убывающих по мере удаления от места концентрации напряжений. В этом случае дело ограничивается появлением местных пластических деформаций, не оказывающих влияния на прочность и жесткость конструкции в целом.

Можно привести другие примеры, когда общие напряжения, достигающие в отдельных точках величины разрушающих, так же не вызывают разрушения конструкции.

Проследим за изменением эпюры нормальных напряжений s в поперечном сечении стальной двухопорной балки при постепенном увеличении нагрузки.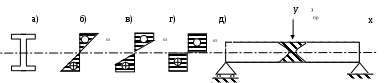





При некотором значении нагрузки напряжения в крайних волокнах сечения достигнут предела текучести s_т . ( M - изгибающий момент, I - момент инерции сечения, y - расстояние от нейтральной оси до произвольного волокна сечения). Но достижение напряжениями в крайних волокнах изгибаемой балки величины s_разр = s_т (s_т - предел текучести) не вызовет разрушения балки; так как во всех промежуточных точках сечения напряжения еще не достигли предела текучести. Дальнейшее увеличение нагрузки будет сопровождаться удлинением одних и укорочением других крайних волокон без увеличения напряжения, а зона текучести будет распространяться внутрь балки.

Нагрузку балки можно увеличить до тех пор, пока напряжения по всей высоте сечения не достигнут предела текучести. Это состояние балки называют предельным: эпюра напряжений s, соответствующая этому состоянию имеет вид двух прямоугольников, разделенных бесконечно узкой полоской (нейтральным слоем). Дальнейшая деформация балки будет происходить уже без увеличения нагрузки. За счет интенсивной пластической деформации части балки, слева и справа от опасного сечения, будут взаимно поворачиваться вокруг нейтральной линии так, как будто бы в этом месте появился шарнир, превративший балку в механизм - пластический шарнир, который в отличие от действительного шарнира, может воспринимать постоянный по величине момент, равный предельному изгибающему моменту.

Таким образом, возникает понятие о нагрузке, соответствующей предельному состоянию, иначе предельной нагрузке, при которой конструкция теряет способность сопротивляться дальнейшему увеличению внешних сил (полностью теряет несущую способность) или получает такие деформации, что последующая ее эксплуатация становится невозможной.

Вспомним, что для всякой конструкции необходимо некоторое минимальное число внешних и внутренних связей, этим обеспечивается равновесие конструкций и ее геометрическая неизменяемость.

При возрастании нагрузок сверх предельных, текучесть распространяется на все больший объем материала и, наконец, при предельном значении нагрузок одна из необходимых связей вследствие распространения пластических деформаций выключается из работы, и равновесие системы нарушается (связь, оказавшаяся в зоне пластичности, деформируется без увеличения усилий в ней, чем и определяется ее выключение из работы). Таким образом, предельная нагрузка - максимальное значение внешней нагрузки, при которой еще возможно равновесие системы, т. е. нагрузка которую в состоянии выдержать данная конструкция в целом.
5.2 СРАВНЕНИЕ МЕТОДОВ РАСЧЕТА НА ПРОЧНОСТЬ ПО ДОПУСКАЕМЫМ НАПРЯЖЕНИЯМ И ПО ПРЕДЕЛЬНЫМ НАГРУЗКАМ.

Определение несущей способности конструкций или назначение размеров поперечных сечений ее элементов может производится по разному.

Можно исходить из условия прочности

(5-1)

где: s_экв - эквивалентное напряжение по той или иной теории прочности,

[s] - допускаемое напряжение материала конструкции.

Согласно этому условию, напряжения ни в одной точке конструкции не должны превосходить величину допускаемого напряжения. Появление пластической деформации хотя бы в одной (опасной) точке конструкции



где: s_т - предел текучести материала конструкции,
означает, что состояние конструкции стало опасным. Обозначая нагрузки, соответствующие этому моменту, символически P_s , получим допускаемое значение нагрузок из условия прочности

(5-2)

где: n - запас прочности.

При этом методе расчета рассматривают конструкцию (или ее элемент) только в упругой стадии деформации, и следовательно, только в условиях линейной зависимости между нагрузками и напряжениями. Поэтому можно заменить понятие «допускаемые нагрузки» понятием «допускаемое напряжение» и в место выражения для P_доп писать

(5-3)

В связи с этим расчет по «опасной» точке часто называют расчетом по допускаемым напряжениям.

Но можно исходить из другого условия, а именно, из условия, чтобы наибольшая действительная (эксплуатационная) нагрузка P_max всей конструкции, умноженная на коэффициент запаса прочности n не превосходила величины предельной нагрузки P_пр ,

(5-4)

Определение грузоподъемности и подбор сечений по этому условию называется расчетом по предельным нагрузкам (или по предельному состоянию).

В статически определимых системах при равномерном распределении напряжений, когда материал по всему сечению используется полностью, расчет по любому из условий (5-1) и (5-4) приводит к одним и тем же результатам.

5.3. Статически определимая система и

равномерное распределение напряжений

В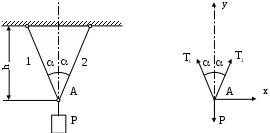
озьмем, например, систему из двух стальных стержней с подвешенным к ним грузом.
Вырезая узел A и рассматривая его равновесие, получаем: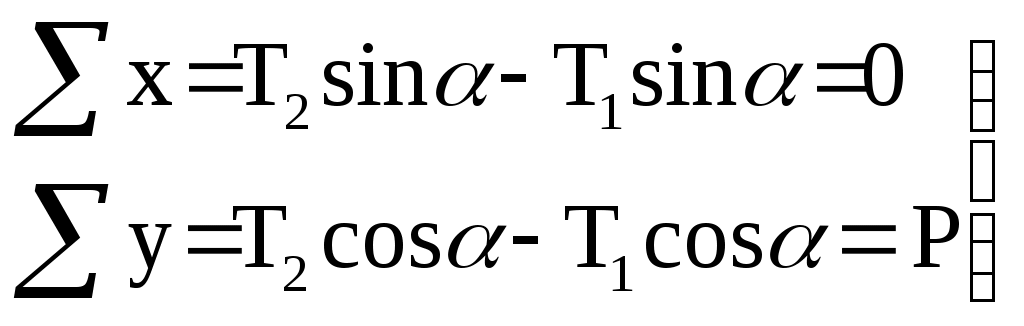

(5-5)

Отсюда находим:

(5-6)


Из расчета по допускаемым напряжениям находим необходимую площадь сечений стержней.

(5-7)

При этом допускаемое напряжение для пластичного материала, выбирается как некоторая часть предела текучести:

(5-8)

Когда напряжения в каком - либо стержне достигнут предела текучести s_T в статически определенной конструкции появится недопустимо большие деформации. Следовательно, предельной нагрузкой следует считать силу P_пр , при которой наибольшее напряжение будет равно пределу текучести, т. е.:



откуда:



Из расчета по предельным нагрузкам (5-9) следует, что:

(5-10)
Отсюда получаем необходимую площадь поперечных сечений стержней:

(5-11)