Лекции по прочности двигателей. Лек_Проч_РД!. Конструкционная прочность элементов ла
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
Подставляя сюданаходим и сравнивая с площадью Fg, найденной при расчете по допускаемым напряжениям, убеждаемся, что при одинаковом запасе прочности n в обоих расчетах получаются одинаковые результаты. Иное наблюдается при расчете статически неопределенных систем, у которых распределение усилий между отдельными элементами всегда зависит от длины и жесткости стержней, входящих в данную систему, то есть, когда имеют место «лишние» связи и неравномерное распределение напряжений. ЛЕКЦИЯ_9 5.4 Статически неопределимая система и неравномерное распределение напряжений Р 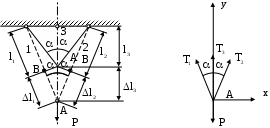 ассмотрим, например, систему трех стержней, нагруженных силой Р. Рассматривая равновесие узла А, находим: 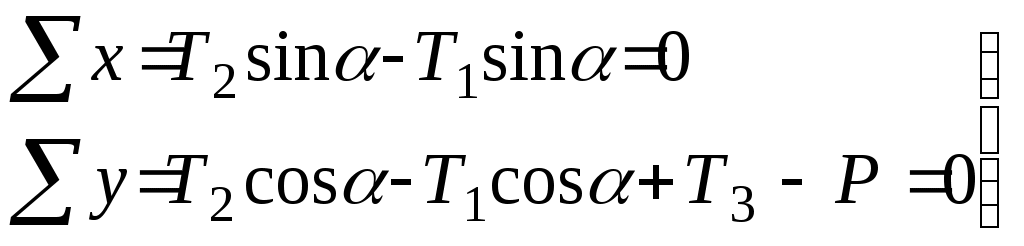 (5-13) Для решения статически неопределимых задач, помимо уравнений равновесия, необходимо составлять дополнительные уравнения, исходя из деформаций системы, так как, например, в данном случае число неизвестных три – (Т1 , Т2 , Т3), а число уравнений статики лишь два. Дополнительное уравнение деформации составляем, рассматривая перемещение узла А. В результате удлинения стержней узел А опустился в положение А1. Так как удлинения малы, то можно принять, что: 1) новый угол между стержнями равен первоначальному , 2) удлинения стержней 1и 2 l1 = l2 =l, равны отрезкам А1В, отсекаемым перпендикулярами, опущенными из точки А на новые положения стержней. Крайние стержни симметричны. Из треугольника АА1В находим Подставляя их в уравнение деформаций и учитывая, что: находим: Вводя условие: то есть, что жесткость стержней одинакова, находим: 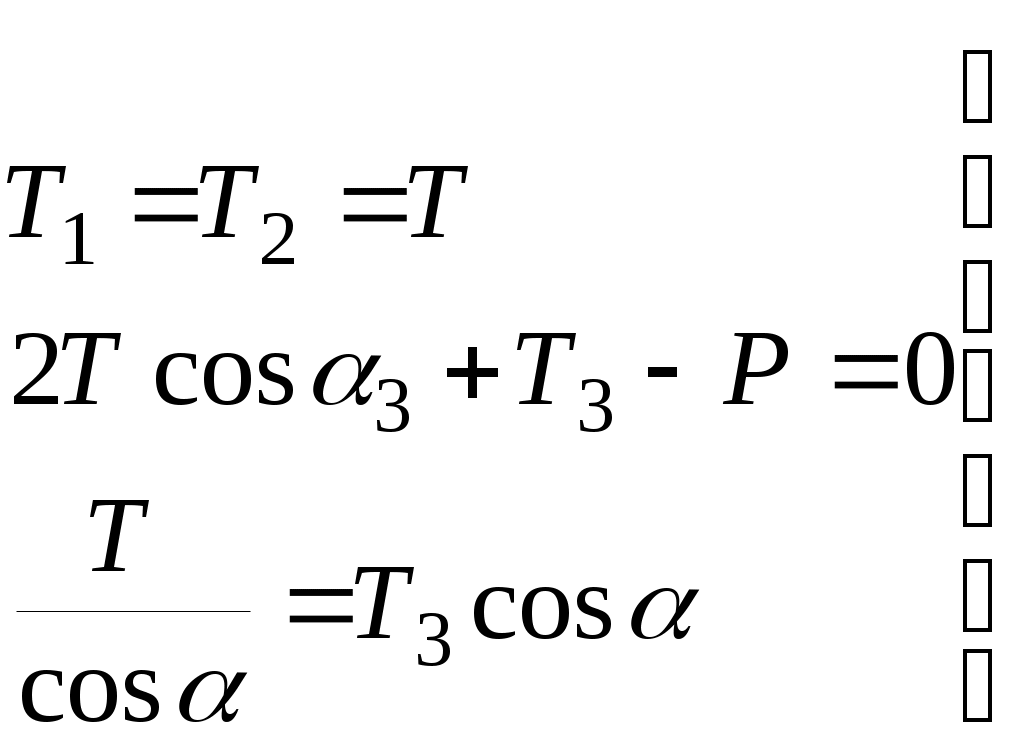 (5-19) (5-19)Решая полученную систему уравнений, находим усилия в среднем и крайних стержнях: Так как cos2<1, то Т3>Т, по допускаемым напряжениям необходимая площадь стержней определяется из условия прочности (3-1) по наибольшему усилию, возникающему в данном случае в среднем стержне, и вычисляется: (5-21) В крайних стержнях такая же площадь поперечного сечения, поэтому напряжения в них меньше и материал этих стержней использован не полностью. Если уменьшить площадь сечений крайних стержней, то усилия изменяться, в частности, усилие в среднем стержне возрастет. Для определения усилий необходимо снова решать уравнения равновесия совместно с удлинением деформации. При расчете по допускаемым напряжениям наибольшая нагрузка Рдоп, которую безопасно может выдержать конструкция, получается, когда наибольшие напряжения достигнут величины [] и усилие в среднем стержне станет равным: (5-22) Из этого условия находим: Умножая допускаемую нагрузку на коэффициент запаса n, получаем предельную нагрузку по допускаемым напряжениям: 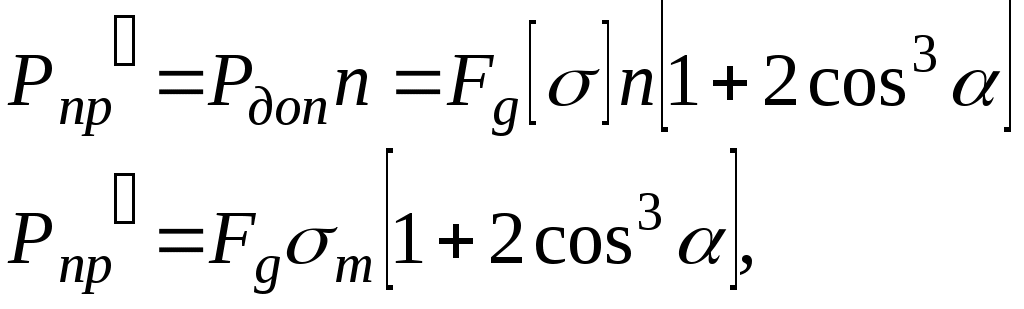 (5-24) (5-24)так как []n=т. Но при этой нагрузке напряжения, равные пределу текучести, возникают только в среднем стержне, а в крайних они меньше т. При дальнейшем увеличении нагрузки средний стержень, изготовленный из пластического материала, легко деформируется, в нем появляются большие остаточные удлинения, а напряжения не растут; он больше не может воспринять возрастания нагрузки и участвует в работе системы, сохраняя постоянное усилие, соответствующее т. Если выходит из работы хотя бы один элемент в статически определимой системе (имеется два стержня 1 и 2), вся конструкция перестает выполнять свое назначение. Этого нельзя сказать про статически неопределимую систему. Так, выход из работы среднего стержня в рассматриваемом примере вовсе не означает нарушения равновесия всей конструкции. В оставшихся двух стержнях напряжения еще не достигли предела текучести, и, следовательно, нагрузку Рпр` можно увеличить на некоторую добавочную величину Р, которая будет восприниматься только двумя стержнями. Вместо трехстержневой системы на добавочную нагрузку работает двухстержневая система. Полный отказ конструкции от работы наступит, когда равные между собой напряжения крайних стержней почти достигнут предела текучести, то есть усилие каждого стержня достигнет предельного значения. и наступит текучесть всей конструкции в целом. Нагрузка Рпр, соответствующая этому состоянию, действительно является разрушающей нагрузкой: к ней уже нельзя ничего добавлять: она вычисляется по уравнению 2Tcos+T3-P=0, в которое нужно подставить предельные усилия стержней Рпр Окончательно: При расчете по предельным нагрузкам, исходя из условий (5-4) находим необходимую площадь поперечных сечений стержней: Сравнивая Fg и Fn видим, что Fg > Fn На самом деле, если 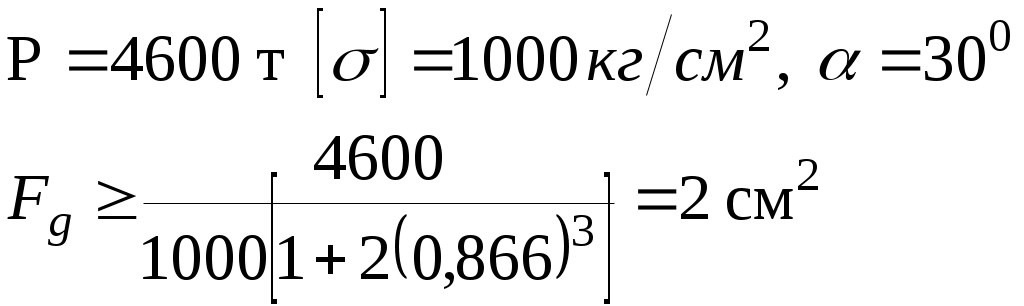 Сравнивая результаты обоих способов расчета, заключаем, что расчет по предельным нагрузкам позволяет проектировать статически неопределенные системы из пластических материалов более экономичными, чем получаемые на основании расчета по допускаемым напряжениям. При расчете по допускаемым напряжениям за предельную нагрузку принимается величина Рпр1, при которой предела текучести достигают напряжения только наиболее нагруженного элемента, а возможности менее нагруженных элементов полностью не используются. При расчете по предельным нагрузкам предельная несущая способность определяется разрушающей силой Рпр, при которой полностью используются материал всех элементов системы. Второй способ расчета позволяет реализовать скрытые запасы прочности статически неопределенных систем, которые первый способ не в состоянии обнаружить благодаря второму способу удается повысить расчетную грузоподъемность и добиться действительной равнопрочности всех частей статически неопределимой конструкции. Кроме того, как видно из приведенного расчета при вычислении предельной нагрузки статически неопределимых частей дополнительных уравнений деформаций составлять не нужно, способ может быть применим лишь в случаях статического нагружения. Можно показать так же, что расчет по предельным нагрузкам, по сравнению с расчетом по допускаемым напряжениям, оказывается более эффективным и при расчете статически определимых систем с неравномерным распределением напряжений при нагружении . Такой случай представляет, например, брус без «лишних» связей, работающий на изгиб. Нагрузка Р=Рs характеризует тот момент нагружения, когда при изгибе напряжения в наиболее удаленный от нейтральной оси точках опасного сечения достигнут предела текучести т. Нагрузка Р=Рпр имеет место тогда, когда в опасном сечении бруса вся площадь сечения охвачена пластическим течением, то есть по всему сечению при изгибе =т. Значит в этом случае Рпр>Рs Таким образом, расчет по предельным нагрузкам может дать эффект по сравнению с расчетом по допускаемым напряжениям при наличии одного из следующих условий: Неравномерное распределение напряжений по опасному сечению. Наличие в конструкции «лишних» связей (при расчете статически неопределимых систем). Как видно из неравенства (5-4), запас прочности при расчете по предельным нагрузкам определяется как отношение Такой подход позволяет отличить запас прочности конструкции от запаса прочности наиболее нагруженного элемента, так как выход последнего из работы еще не обязательно означает наступление предельного состояния для всей конструкции в случае, если она статически неопределима. Значение допускаемых нагрузок получаем из условий прочности: При использовании метода предельных нагрузок, кроме точности определения величин напряжений, существенную роль играет выбор теории прочности. Исследованием установлено, что для пластических материалов хорошо согласуется с опытом данные теории энергии формоизменения (предельное состояние наступает тогда, когда в единице объема материала накопиться определенная энергия формоизменения). Метод расчета на прочность применяемый в авиации и судостроении по существу близок к расчету по предельным нагрузкам. Он связан с использованием так называемых редукционных коэффициентов, учитывающих возможность потери устойчивости отдельными элементами конструкции наличием начальных несовершенств формы элементов (например, прогибы) и другие факторы, которые условно можно характеризовать как изменение модуля упругости данного элемента. По форме он является методом расчета по разгружающим нагрузкам. |
