Лекции по прочности двигателей. Лек_Проч_РД!. Конструкционная прочность элементов ла
 Скачать 1.21 Mb.
|
Упругость.Диаграммы зависимости напряжения от деформации показывают, как ведет себя материал при нагружении. Когда образец материала разгружается, то есть когда нагрузка постепенно уменьшается до нуля, удлинение, которое возникло при нагружении, будет частично, или полностью исчезать. Это свойство материала, который при разгрузке стремиться вернуться к своей первоначальной форме, называется упругостью. Если стержень полностью восстанавливает свою первоначальную форму, то его называют идеально упругим, если же частично – то частично упругим. В последнем случае удлинение, которое остается в стержне после того, как снята внешняя нагрузка, называется остаточной деформацией. Максимальное напряжение, которое характеризует верхнюю границу упругой области на диаграмме, называется пределом упругости. Для большинства материалов, в том числе и для стали, предел упругости и предел пропорциональности практически совпадают. Однако, например, у резины свойство упругости сохраняется далеко за пределом пропорциональности. Практика расчётов деталей машин и конструкций часто требует аналитического представления данных испытаний образцов. В частности, в области упругого деформирования наиболее распространенным и достаточно точно отражающим свойство многих реальных материалов, оказывается линейное соотношение между напряжениями и деформация:  (2.5)После определения числа Е на основании обработки экспериментальных данных соотношение (2.5) получает статус физического закона и называется законом Гука по имени Роберта Гука, который сформулировал его более чем 300 лет назад. Коэффициент пропорциональности Е в (2.5) называется модулем Юнга и представляет собой важнейшую характеристику упругости материала. Второй важнейшей характеристикой поведения материала в упругом состоянии является коэффициент Пуассона (2.4). В таблице 2.1 приведены значения этих величин для некоторых материалов. Таблица 2.1
Упруго - пластические состояния.Установив упругие свойства материала, располагаем пределом упругости и соотношением между напряжением и деформацией, представленным аналитически в форме закона Гука (2.5). Дальнейшие исследования поведения материалов связаны с внешним нагружением, выводящим возникающие в нём напряжения за пределы упругости. При этом после разгрузки в металле возникают остаточные деформации. На рисунке 2.4 показан примерный вид кривой «напряжение- деформация» для стального образца. Выведя образец за предел упругости, разгрузим его – при этом обнаруживается остаточная или пластическая деформация п. Процесс разгрузки стали следует примерно линейному закону, причем участок разгрузки, практически параллелен линейному участку первоначального нагружения. Состояние материала, при котором напряжение превышает предел упругости, называют упруго - пластическим. Общую деформацию в любом упруго - пластическом состоянии принято представлять формально суммой упругой у и пластической п деформаций уп . (2.6) Таким образом, физическим признаком упруго- пластического состояния является наличие остаточной деформации. Отличительной чертой аналитического описания упруго-пластического состояния является неоднозначная зависимость между напряжениями и деформациями. При этом различают процесс активного нагружения, разгрузку, повторную нагрузку, многократные нагрузки и разгрузки. Аналитическое представление процесса активного нагружения за пределом упругости всегда опирается на определенный предел упругости у(у). Располагая этой точкой и участком кривой упруго-пластических состояний, полученных из опытов с монотонным возрастанием нагрузок и деформаций, можно по разному аналитически описать экспериментальные данные. Например, для деталей типа дюралюминиевых сплавов удовлетворительной является степенная зависимость вида Ап, (2.7) где А и n – константы материала, определяемые обработкой экспериментальных данных. Рисунок 2.4, кроме прочего, иллюстрирует эффект повышения предела упругости материала в результате его предварительного пластического деформирования. Это свойство конструкционных материалов называют деформационным упрочнением, нагартовкой или наклепом. В заключение остановимся на описании ещё одного интересного факта. Допустим, что имеется возможность испытания одного и того же образца не только на растяжение, но и на сжатие. Другими словами, испытания проводятся с переменой знаков напряжений и деформаций. Предположим, симметричный в отношении растяжения и сжатия материал вывели растяжением в упруго-пластическое состояние и разгрузили. Как было сказано, при повторном растяжении образца обнаруживается расширение области упругих деформаций – деформационное упрочнение. Если теперь материал сжимать (рисунок 2.5) – наблюдается сужение области упругих деформаций – разупрочнение. Описанное явление в литературе называют эффектом Баушингера. 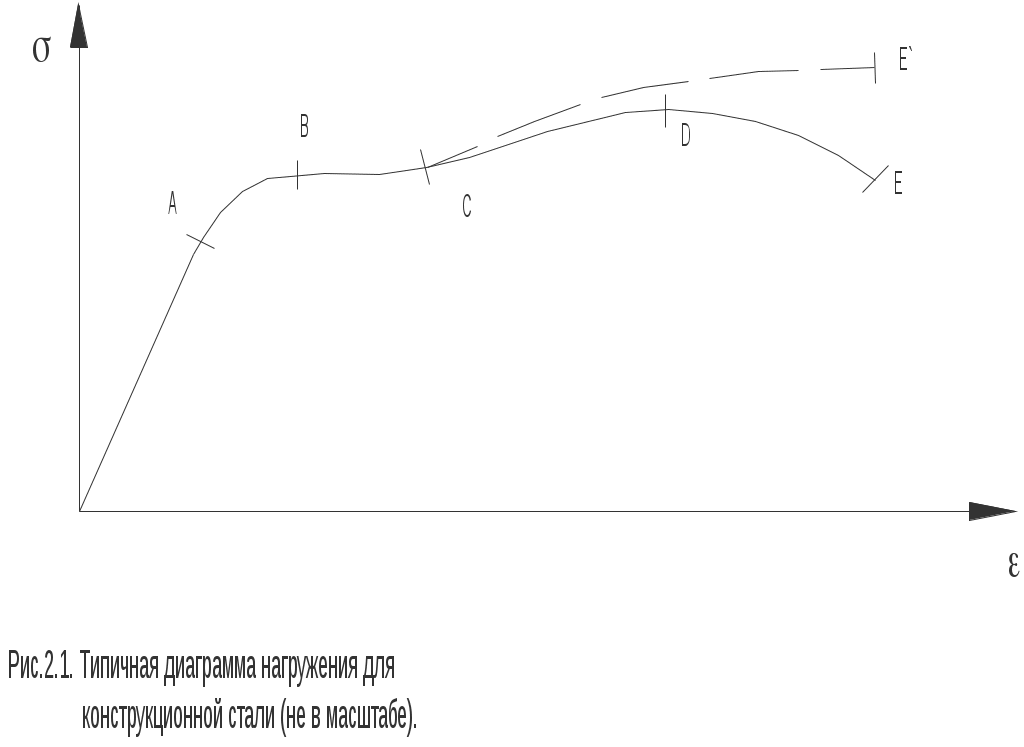 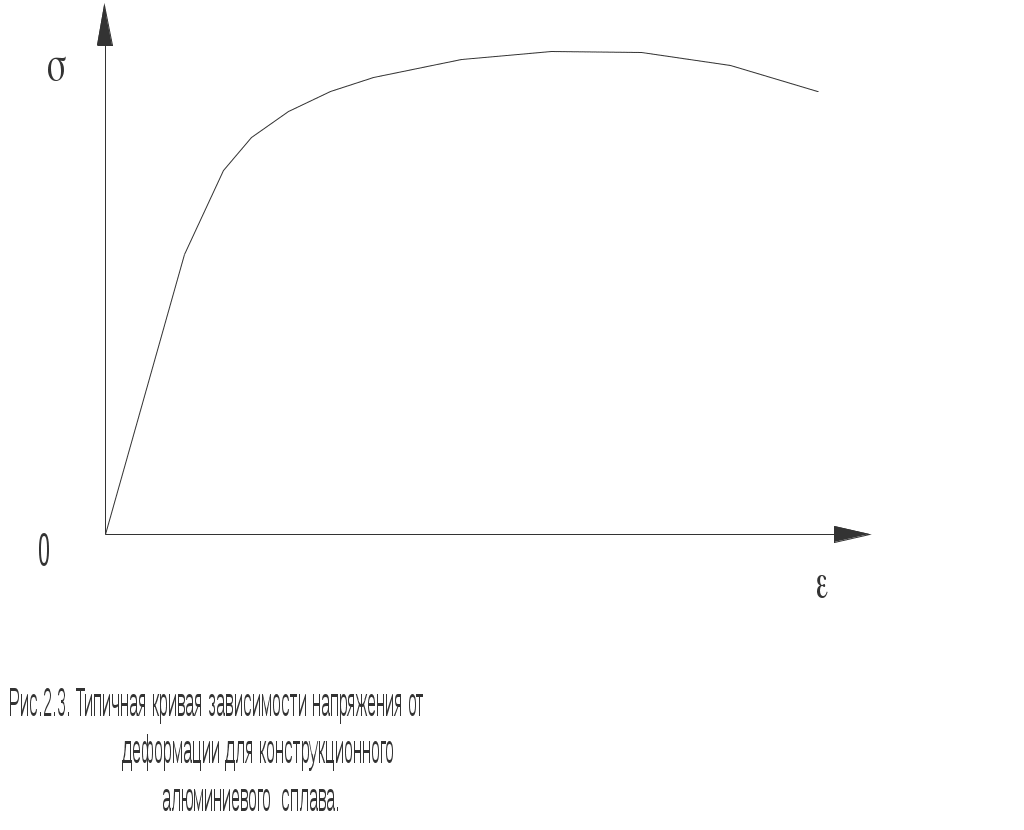  ЛЕКЦИЯ_3 2. Основы теории напряжений 2.1. Обозначение составляющих напряжений.Тензор напряжений.Величины всяких усилий (как внешних, так и внутренних) характеризуются интенсивностью, то есть величиной усилия, приходящегося на единицу площади поверхности, на которую они действуют. При рассмотрении внутренних усилий эту интенсивность называют напряжением. В дальнейшем условимся называть «волокном тела» совокупность его точек, расположенных вдоль какой–либо геометрической линии, а «линейным элементом тела» - бесконечно малый (дифференциальный) отрезок какого–либо волокна. «Слой тела» - совокупность его точек, расположенных на некоторой поверхности, а «элементарная площадка тела» - бесконечно малый элемент какого–либо слоя. Для обозначения интенсивности сил удобно применять следующую систему. Если в заданном теле, некоторым образом ориентированном в прямоугольной системе координат (x, y, z), рассматриваемая точка лежит на какой–либо элементарной площадке, внешняя нормаль к которой,  , и она не параллельна в общем случае ни одной из координатных осей, то интенсивность усилия или, другими словами, полное напряжение для данной точки на данной площадке будем обозначать  . Очевидно, что направление вектора полного напряжения совпадает с направлением усилия  , приходящегося на рассматриваемую элементарную площадку F, так как по определению справедливо равенство: . (2.1)Заметим, что формулировка напряжения в виде (2.1) предполагает тело сплошным, непрерывным. Проекции полного напряжения  на координатные оси x, y, z будем обозначать соответственно  ,  ,  . Очевидно выполнение равенства . (2.2)Таким образом, если обозначение напряжения имеет два индекса, то первый характеризует нормаль к площадке, на которой развивается напряжение, а второй индекс - ту координатную (или характерную) ось, которой параллелен вектор напряжения. В свете сказанного составляющие напряжений, параллельные координатным осям и действующие по трём взаимно перпендикулярным площадкам, параллельным трём координатным плоскостям, теперь будут обозначаться так: на площадке, нормаль к которой параллельна оси ОХ: Pxx, Pxy, Pxz; на площадке, нормаль к которой параллельна оси ОУ: Pyy, Pyx, Pyz; на площадке, нормаль к которой параллельна оси OZ: Pzz, Pzx, Pzy. Заметим, что составляющие Рxx, Рyy, Рzz, как нормальные к соответствующим площадкам, представляют нормальные напряжения, а остальные компоненты - касательные напряжения. Будем сохранять систему обозначений, принятую в сопротивлении материалов, и нормальные напряжения будем обозначать , а касательные - . Причём, так как у нормальных напряжений первый и второй индекс всегда совпадают, то их не принято писать дважды. Поэтому компоненты напряжений на трёх координатных площадках обозначают так: x; y; z; xy; xz; yx; yz; zx; zy. Правила знаков.Нормальное напряжение принято считать положительным, если оно является растягивающим, и отрицательным, если оно сжимающее. За положительное направление касательных напряжений принимаются положительные направления соответствующих координатных осей, если растягивающее нормальное напряжение на той же площадке имеет направление, совпадающее с положительным направлением той оси координат, параллельно которой действует упомянутое нормальное напряжение. На рисунке 2.1 указаны обозначения всех составляющих (компонент) напряжений, действующих по граням бесконечно малого параллелепипеда, причём на рисунке все направления напряжений показаны положительными. При этом в случае малости граней параллелепипеда одноимённые и параллельные напряжения для каждой пары параллельных граней будут практически совпадать по величине - это следует из уравнений равновесия. Кроме того, в курсе сопротивления материалов доказывался (на примере плоского напряжённого состояния) закон парности касательных напряжений: если на какой–либо площадке действует касательное напряжение, то на ортогональной ей площадке всегда возникает равное ему по величине и создающее момент противоположного знака касательное напряжение, то есть применительно к рисунку 2.1 имеем: xy=yx; xz=zx; yz=zy. (2.3) Таким образом, всего с учётом (2.3) неизвестных компонент напряжений будет не девять, а шесть. Расположим эти напряжения в виде следующей наглядной таблицы: 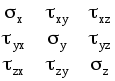 . (2.4)В строках расположены компоненты, возникающие на одной и той же площадке, в столбцах - компоненты, имеющие направление, параллельное какой–либо оси. В связи с этим у напряжений, расположенных в строке, общим является первый, в столбце - второй индекс. При таком способе построения таблицы нормальные напряжения всегда располагаются вдоль главной диагонали, а одинаковые по величине касательные напряжения - симметрично главной диагонали. К 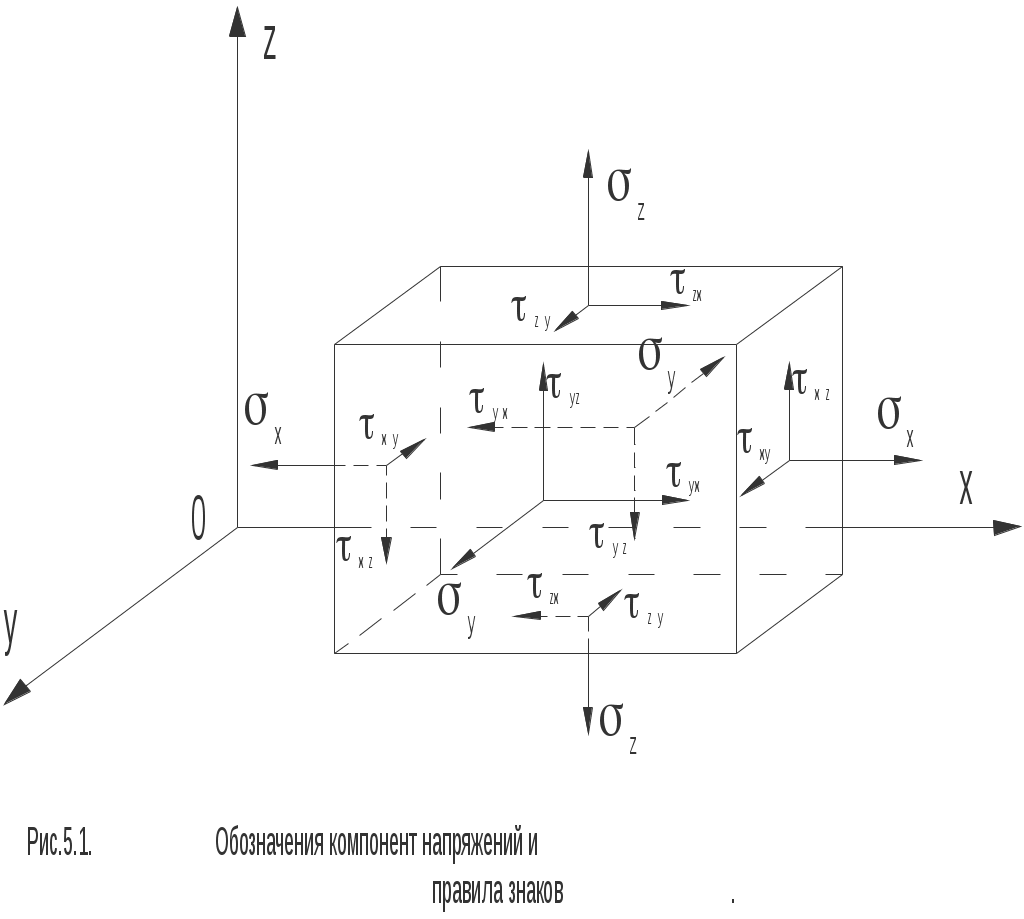 вадратную симметричную матрицу (2.4) называют тензором напряжений. Таким образом, в отличие от вектора, который определяется тремя скалярными величинами (компонентами), тензор напряжений определяется тремя векторами. |