Лекции по прочности двигателей. Лек_Проч_РД!. Конструкционная прочность элементов ла

• Название: Конструкционная прочность элементов ла
• Анкор: Лекции по прочности двигателей
• Дата: 28.06.2022
• Размер: 1.21 Mb.
• Имя файла: Лек_Проч_РД!.doc
• Тип: Анализ; #618558
• страница: 5 из 7

2.2 Понятие тензора и закон преобразования его компонент.

В курсах физики, теоретической механики и сопротивления материалов многократно использовались понятия скаляра и вектора.

Известно, что физические величины для определения которых достаточно знать одно число, называют скалярами. Например, это температура, плотность, масса, работа силы. Сравниваться между собой могут только скаляры одной размерности. Два скаляра одной размерности равны, если их знаки и численные значения, получающиеся при измерении одной и той же единицей измерения, одинаковы.

Часто приходится иметь дело с величинами, для определения которых кроме численного значения необходимо указать их направление в пространстве. Это может быть перемещение, скорость, ускорение, сила, момент силы, напряжение электрического поля и др. Такие величины называются векторами. Для их определения нужны три числа - например, проекции вектора на координатные оси.

Действие над скалярами и векторами изучались в соответствующих разделах курса высшей математики.

Но, как показывает практика, скаляр и вектор вовсе не исчерпывают классы физических величин. Многие из них имеют гораздо более сложную структуру, и для их определения недостаточно знать только числовые значения и направление. Если, как было сказано, скаляру для его однозначного определения достаточна одна численная компонента, для определения вектора - три компоненты, то более сложные объекты требуют для своего описания большего числа компонент.

Так, рассмотрение совокупности векторов напряжений на всевозможных площадках, которые можно провести через некоторую материальную точку, требует уже девяти чисел, а для описания деформации упругого тела в точке необходимо уже 3³=27 чисел. Упругие свойства анизотропного тела требуют для полной характеристики 3⁴=81 число.

Числа (или функции), которые полностью определяют величину в какой–то системе координат, называются компонентами этой величины.

С этой точки зрения оказалось удобно рассматривать такие величины, как тензоры различных рангов:

скаляр (3⁰=1 компонента) - тензор нулевого ранга;

вектор (3¹=3 компоненты) - тензор первого ранга;

величина, имеющая 3^п компонент - тензор ранга п.

Компоненты тензора могут быть как числами, так и функциями, например, времени или пространственных координат.

Физические величины можно рассматривать и определять в различных системах координат - например, в декартовых координатах с различным началом и различным образом ориентированных. При этом компоненты одной и той же величины (тензора) могут иметь различные значения в различных системах координат. Однако, в связи с тем, что эти компоненты определяют одну и ту же физическую величину, закон преобразования их компонент при переходе из одной системы координат в другую не может быть произвольным. Этот закон должен вытекать как из природы рассматриваемой величины (для скаляра - один закон, для вектора - другой и т. д.), так и из свойств пространства, в котором выбираются системы координат.

Произвольность выбора начала (перенос) координатных систем отражает однородность пространства. Равноправность любой ориентации (поворот) координатных систем означает изотропность пространства.

В однородном и изотропном пространстве все координатные системы равноправны в том смысле, что описание физических величин или явлений в них (физических законов) не зависят от конкретного выбора системы координат.

Это означает следующее. Пусть в однородном и изотропном пространстве выбраны две произвольные системы координат К и К, которые могут иметь различное начало и различную ориентацию. Тогда закон, сформулированный в системе К через компоненты величин, относящихся к этой системе, должен иметь тот же вид, что и тот же закон, сформулированный в системе координат К через компоненты, относящиеся к системе К.

Это требование к правильно сформулированным законам носит название требования инвариантности.

Например. Если длина какого–то отрезка, вычисленная в системе координат К, равна S, то и в другой системе координат К она должна быть такой же. Математически этот факт может быть выражен тем, что величина s²=x_i²+y_i²+z_i², имеет одинаковое численное значение независимо от того, в какой из прямоугольных декартовых систем x_i, y_i, z_i находятся x_i ,y_i ,z_i - разности координат конца и начала отрезка.

Примечание. Независимость описания от выбора системы координат является не единственным требованием, предъявляемым к величинам и законам. В качестве другого такого требования укажем на условие независимости формулировки законов от выбора системы единиц измерения. На этом факте построена теория размерностей.

Тензоры второго ранга.

Как уже отмечалось, некоторые геометрические объекты, а также целый ряд физических свойств, требуют для своей характеристики более трёх чисел (или функций).

Это приводит к понятию величин, комплекс свойств которых сложнее, чем у векторов и скаляров. Они не могут быть составлены в виде простого набора векторов или скаляров. Это - качественно новые величины, отвечающие физическому или геометрическому смыслу описываемых объектов.

Рассмотрим сказанное на примере тензора напряжений.

Напряжённое состояние в точке считается известным, если известно напряжение на любой произвольной площадке, проходящей через данную точку.

Таким образом, вектор напряжения Р в среде является функцией точки и ориентации в пространстве площадки, на которой рассматривается напряжение:

, (2.6)

где r - радиус–вектор точки;

n - орт нормали к площадке.

Вектор напряжения принципиально не годится для характеристики напряжённого состояния среды в точке, так как при этом необходимо рассматривать бесконечную совокупность Р на всевозможных площадках, проходящих через точку (рисунок 2.2).

Оказалось возможным определить такую величину, которая является однозначной функцией точки, то есть не зависит от ориентации площадки в пространстве и в то же время позволяет вычислить напряжение на любой площадке с заданной нормалью.

Рассмотрим вырезанный в окрестностях точки М элементарный материальный тетраэдр, оси которого совпадают с осями декартовой системы координат (рисунок 2.3).

Обозначим площадки граней, перпендикулярных к осям ох₁, ох₂, ох₃ системы координат (К), соответственно через dS₁, dS₂, dS₃,а площадь наклонной грани с нормалью n - через dS_n. Действие внешней по отношению к тетраэдру на эти грани выражается соответственно в напряжениях Р₁, Р₂, Р₃.

Учитывая, что инерционные силы, возникающие при движении тетраэдра, пропорциональны его массе ,

где - плотность материала, являются малыми более высокого порядка по сравнению с членами, содержащими элементарные площади ,где ,

уравнение равновесия тетраэдра в векторной форме записывается так:

. (2.7)

Но поскольку,

,

где n_i - направляющий косинус орта в рассматриваемой системе координат, то

. (2.8)

При записи (2.8) использовано известное правило суммирования А. Эйнштейна по индексам.

Проекции вектора напряжения на площадке с нормалью на оси координат системы (К) равны:

p_nk=p_ikn_i , (2.9)

где p_ik - совокупность девяти напряжений, нормальных при i=k и касательных при , на трёх взаимно перпендикулярных площадках в окрестностях точки М (рисунок 2.4).

Эти девять величин, очевидно, никак не связаны с ориентацией площадки, на которой определяется напряжение , а связаны лишь с координатой точки М. В то же время знание р_ik позволяет вычислить на любой площадке, если известна её ориентация в пространстве. В каждой точке среды однозначно определена одна физическая величина, т. е. девять чисел P_ik, которая является исчерпывающей характеристикой напряженного состояния среды в точке.

Совокупность этих величин P_ik определяет тензор второго ранга, который носит название тензора напряжений.

Кстати, неизвестно, на уровне автора, техническое приложение тензора второго ранга, кроме тензора напряжений (деформированное состояние считается эквивалентным напряжённому в рамках соотношений теории упругости).

Рассмотрим закон преобразования девяти величин P_ik при изменении системы координат.

Не ограничивая общности, можно считать, что i-я ось новой системы координат (К) направлена по нормали (ибо при определении P_ik никаких ограничений на n не накладывалось).

Если i₁, i₂, i₃ - орты системы (К), а (i₁, i₂, i₃) - орты системы (К), то ,

Проекция n на l - ю ось системы (К) равна ,

где - косинус угла между i- й осью системы (К) и l - й осью системы (К).

Таким образом :

.

Спроектируем последнее равенство на к - ю ось системы (К):

,

или окончательно:

. (2.10)

Выражение (2.10) является искомым законом преобразования девяти величин P_ik при изменении декартовой системы координат.

Примечание: при выводе (2.10) использовалось правило суммирования А. Эйнштейна (то же правило использовалось при записи выражения (2.8)).

Правило суммирования по индексам (правило А. Эйнштейна).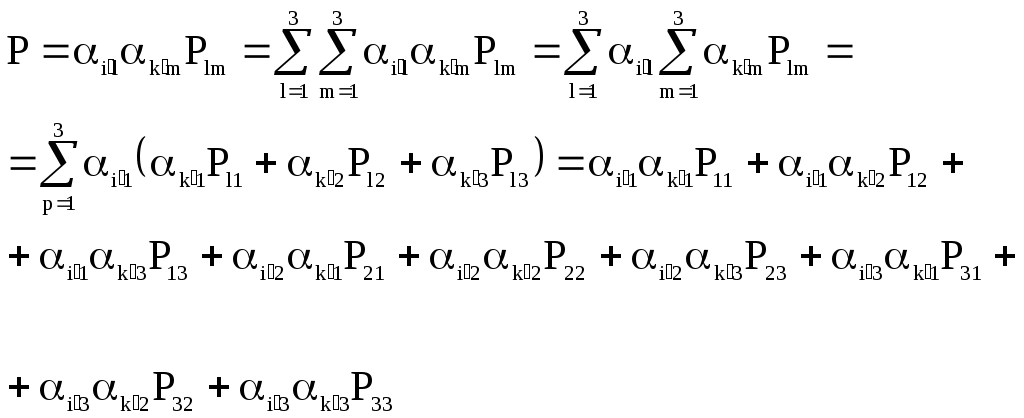

Если во входящем в структуру какого–либо выражения одночлене имеются дважды повторяющиеся индексы (неважно, где они расположены - вверху или внизу - но не путать с показателем степени!), то по этим индексам подразумевается суммирование от 1 до 3.

Таким образом, например, выражения А_ii, A_iBⁱ, A_iB^kCⁱ означают соответственно:

,

,

.
Несомненным достоинством правила суммирования по индексам является компактность записи громоздких выражений. Недостаток - сложность восприятия формул без привычки.

Таким образом, тензор 2-го ранга - это величина определяемая в любой системе координат девятью числами (или функциями) А_ik, которые при изменении системы координат преобразуются в другие девять чисел А_ik по закону (4.5):

, (2.10)

где - косинус угла между i-й осью новой системы и l-й осью исходной системы координат.

Заметим, что если все компоненты тензора обращаются в нуль в какой–либо системе координат, то они равны нулю в любой другой системе вследствие однородности закона преобразования (2.10).

Тензор второго ранга удобно и принято записывать в виде таблицы (матрицы):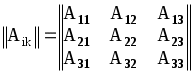



В заключение ещё одно замечание. В механике деформируемого твёрдого тела при работе с выражениями с индексами часто используется символ (дельта) Кронекера: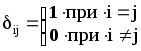

(2.11)

Н
апример, выражение m_ij-_ij означает матрицу m_ij, из компонент которой, расположенных вдоль главной диагонали вычитается некоторое число .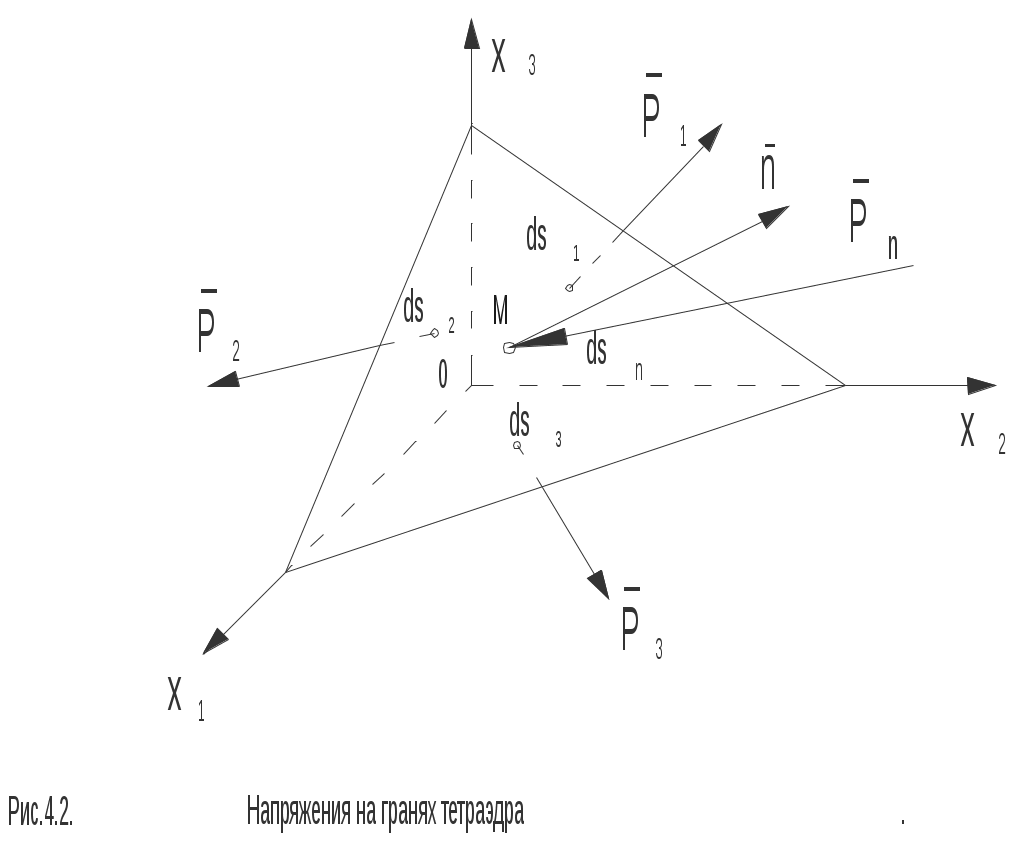






ЛЕКЦИЯ_4

2. 3 Исследование напряжённого состояния в данной точке тела.

Если считать, что компоненты тензора напряжений в некоторой координатной системе (x, y, z) известны, то в соответствии с (2.9) проекции полного напряжения, действующего на косой площадке с нормалью , характеризуемой направляющими косинусами l, m, n относительно координатных осей x, y, z соответственно, записываются так: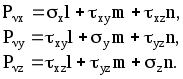

(2.12)

Формулами (5.5) можно воспользоваться для исследования напряжённого состояния в любой точке тела и на любой площадке.

Для того, чтобы найти величину нормального напряжения на той же наклонной площадке, необходимо спроектировать компоненты (2.12) на нормаль  и провести алгебраическое суммирование проекций:

_=Р_хl+P_ym+P_zn=_xl²+_ym²+_zn²+2(_xylm+_xzln+_yzmn). (2.13)

Заметим, что в частном случае плоского напряжённого состояния, например, при n=0 из (5.6) вытекает:

_=_xl²+_ym²+ 2_xylm ,

или, с учётом того, что в плоском случае arccosm и arccosl - дополнительные углы, т. е. l=cos; m=sin, из (2.13) вытекает известное соотношение сопротивления материалов:

_=_xcos²+_ysin²+_xysin2.

С учётом (2.12) и (2.13) касательное напряжение на косой площадке определяется так:

. (2.14)

2.4. Главные напряжения и главные площадки при объёмном напряжённом состоянии.

Напряжённое состояние в точке - физическое состояние, определяемое свойствами материала и внешними воздействиями. А, между тем, характеризовали его компонентами тензора напряжений в системе координат, совершенно случайно ориентированной в пространстве. Естественно попытаться найти такую систему координат, которая связана с физическим состоянием и в котором напряжённое состояние реализуется наиболее просто. Например, пусть на координатных площадках в такой системе координат полностью отсутствуют касательные напряжения. Такие три оси, и соответствующие им площадки, называются главными осями и главными площадками - они существуют в каждой точке тела.

Пусть наклонная площадка является главной. Тогда полное напряжение на ней совпадает с нормальным, так как касательное напряжение на ней отсутствует по определению. Из этого условия определяем главные напряжения и положение главных площадок. Обозначим искомое главное напряжение временно  и, проектируя его на координатные оси, получаем:

; ; .

Теперь уравнения (5.5) записываются так: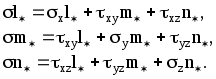



Кроме того, имеется, известное из аналитической геометрии, условие нормировки для направляющих косинусов:

. (2.15)

Последние четыре уравнения содержат четыре неизвестных (главное напряжение  и три направляющих косинуса l_*, m_*, n_*). Перепишем первые три уравнения так: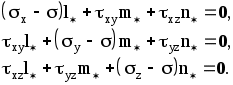

(2.16)

Последние три уравнения - линейные и однородные относительно направляющих косинусов. Кроме того, в силу нормировки направляющие косинусы не могут быть одновременно равны нулю. Следовательно, чтобы существовало ненулевое решение системы (2.16), её главный определитель должен быть тождественно равен нулю: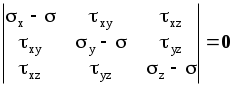

.

Р 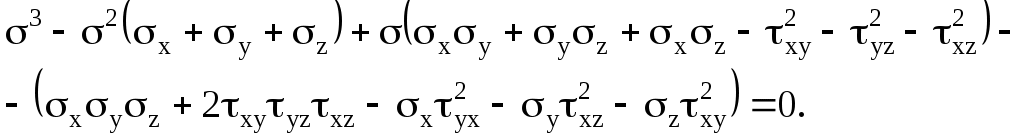аскрывая определитель, получаем полное кубическое уравнение: (2.15)

Структура уравнения (2.17) такова, что оно всегда имеет три действительных корня:

₁>₂>₃ ,

где ₁,₂,₃ - искомые главные напряжения.

Заметим, что каждому из них соответствует своя главная площадка и все они - ортогональны друг другу.

Заметим, что формулу (2.13) для определения нормального напряжения на наклонной площадке с нормалью  можно записать в виде:

. (*)

Сформулируем и решим такую задачу: найдём площадки ( ), содержащую данную точку, нормальные напряжения на которых достигают экстремального значения. Так как направляющие косинусы связаны между собой условием нормировки:

, (**)

то необходимо найти экстремум функции (*), при наличии неявной связи (**) между переменными. Такого класса задачи позволяет изящно решать метод неопределённых множителей Лагранжа. Известно, что задача сводится к отысканию безусловного экстремума функции вида:

,

где  - неопределённый множитель Лагранжа, в данном случае искомое экстремальное напряжение.

Для этого достаточно вычислить её первые частные производные по l_*, m_*, n_* и приравнять полученные уравнения нулю: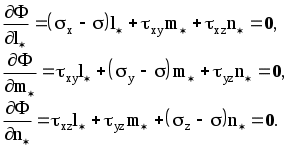



Полученные уравнения в совокупности с (*) позволяют определить величины , l_*, m_*, n_*. Заметим, что задача эквивалентна полученным ранее уравнениям (2.15) и (2.16).

Таким образом, пришли к важному выводу: главные напряжения на главных площадках являются экстремальными нормальными напряжениями в данной материальной точке.