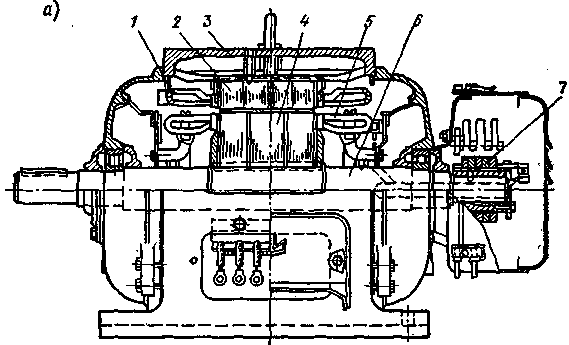
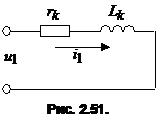Конструкция трансформаторов Трансформатор представляет собой линейный электромагнитный аппарат
 Скачать 1.16 Mb.
|
|
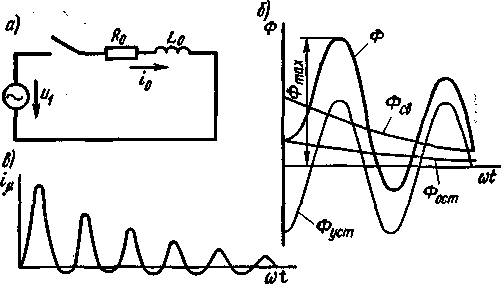
13. Автотрансформаторы.В обычных трансформаторах первичные и вторичные обмотки имеют только магнитную связь. В автотрансформаторах первичные и вторичные обмотки имеют магнитную и электрическую связь, что экономически выгодно. При этом первичная обмотка w1 включена в сеть параллельно, а вторичная w2 – последовательно. 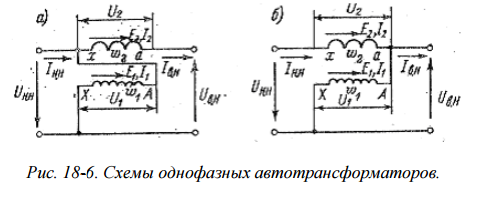 Ввиду электрической связи обмоток изоляция каждой из них относительно корпуса должна выдерживать напряжение сети Uвн. На рисунке 18-6 (а) первичная обмотка включена в сеть низшего напряжения, а на рис. (б) – в сеть высшего напряжения. В обоих случаях напряжение вторичной обмотки U2 складывается с напряжением Uнн и, пренебрегая падением напряжения, Uвн = Uнн + U2. Автотрансформатор может служить как для повышения, так и для понижения напряжения. Применение автотрансформаторов тем выгоднее, чем коэффициент трансформации kтр ближе к единице 1. Обычно они используются при kтр ≤ 2,5. Они находят широкое применение для соединения высоковольтных сетей разных напряжений (110, 154, 220, 330, 500, кВ) энергетических систем. Внутренняя, или расчетная, мощность автотрансформатора, передаваемая посредством магнитного поля из первичной обмотки во вторичную, как и в обычных трансформаторах, равна Sp = E1I1 = E2I2. Внешняя, или проходная, мощность автотрансформатора, передаваемая из одной сети в другую и равная Sпр = UннIнн = UвнIвн, больше Sp, так как часть мощности передается из одной сети в другую непосредственно электрическим путем. 14. Регулирование напряжения транформаторов. Принципы регулирования. При эксплуатации трансформаторов довольно часто возникает необходимость регулирования вторичного напряжения. При этом различают два основных случая: 1) стабилизация вторичного напряжения при незначительном (на 5 — 10%) изменении первичного напряжения, что происходит обычно из-за падения напряжения в линии; 2) регулирование вторичного напряжения (из-за особенностей технологического процесса) в широких пределах при неизменном (или мало изменяющемся) первичном напряжении. В обоих случаях вторичное напряжение регулируется путемизменения коэффициента трансформации, т. е. соотношения между числами витков первичной и вторичной обмоток. В первом случае при небольших изменениях первичного напряжения можно изменять число витков либо первичной, либо вторичной обмотки. Например, при снижении первичного напряжения соответственно уменьшают число витков первичной обмотки так, чтобы ЭДС витка осталась неизменной. Поскольку число витков вторичной обмотки не изменяется, неизменной останется и ЭДС вторичной обмотки. При возрастании первичного напряжения соответственно увеличивают число витков первичной обмотки. Во втором случае, когда требуется регулировать вторичное напряжение при неизменном первичном, изменяют число витков вторичной обмотки. Изменять число витков первичной обмотки в этом случае нельзя, так как это приведет к изменению магнитного потока трансформатора и, как следствие, к его перегреву илиплохому использованию. Кроме того, очевидно, что получить малое выходное напряжение U2 = U1w2/w1при неизменном числе витков вторичной обмотки практически невозможно, так какпри этом необходимо иметь большое число регулировочных витков*. Переключение ответвлений обмоток w1 и w2 может осуществляться при отключении трансформатора от первичной и вторичной сетей (переключение без возбуждения) или под нагрузкой (регулирование под нагрузкой). Существуют также трансформаторы с плавным регулированием напряжения, в которых плавно изменяют число витков w2 или магнитный поток Ф2, охватываемый этой обмоткой. 15. Переходный процесс при включении трансформатора без нагрузки. Рассмотрим случай включения однофазного трансформатора при разомкнутой вторичной обмотке. Исходя из схемы замещения трансформатора при холостом ходе (рис. 2.64, а), можно составить уравнение L0di0/dt + R0i0 = U1msin (ωt + α0). (2.94) Это уравнение по структуре подобно уравнению (2.85) и отличается от него только коэффициентами L0и R0 (вместо Lк и Rк). Однако пользоваться им нельзя, так как L0 определяется потоком, замыкающимся по стали, и, следовательно, является переменной величиной.
В уравнении (2.94) вместо переменной i0 целесообразно ввести переменную Ф, которую можно определить из уравнения L0i0 — w1Ф. При этом получим w1dФ/dt + w1(R0/L0)Ф = U1msin (ωt + α0). (2.95) Приближенное решение уравнения (2.95) можно получить, полагая L0 ≈ const; погрешность в данном случае небольшая, так как R0<< ωL0. По аналогии с уравнением (2.85), имеющим ту же структуру, имеем Ф = Фуст + Фсв = Фт sin (ωt + α0 - φ0) + Се -(Ro/Lo)t. (2.96) Так как ωL0 >> R0, то φ0 ≈ π/2 и, следовательно, Ф = - Фm cos(ωt + α0) + Се -(Ro/Lo)t. (2.97) Постоянную интегрирования найдем из начальных условий: при t = 0 поток Ф = ±Фост, где Фост— остаточный магнитный поток, достигающий иногда в трансформаторе значения 0,5Фт. При этом постоянная интегрирования С = Фт cos α0 ± Фост, а выражение (2.97) принимает вид
Наиболее благоприятные условия включения при α0 = π/2 и Фост = 0. В этом случае Ф=Фт sin ωt, (2.99) т. е. с первого же момента в трансформаторе устанавлива¬ется номинальный магнитный поток. Наиболее неблагоприятно включение трансформатора при α0 = 0 и противоположном по знаку потоку Фост. Тогда Ф = - Фтcos ωt + (Фт + Фост) е -(Ro/Lo)t. (2.100) В этом случае через полпериода после включения поток достигает максимума (рис. 2.64,6):
Двукратной амплитуде потока соответствует намагничивающий ток Iμmах, в десятки и сотни раз (рис. 2.64, в) превышающий амплитуду установившегося тока холостого хода, что объясняется насыщением стали. Это следует учитывать при регулировании защитных устройств, чтобы не получалось ложных срабатываний защиты при включении трансформатора. 16. Переходный процесс при внезапном коротком замыкании трансформатора. Ограничимся рассмотрением процесса короткого замыкания однофазного трансформатора, работавшего до этого в режиме холостого хода (рис. 50). Примем допущение, что напряжение сети  не зависит от режима работы трансформатора, а также будем полагать, что магнитопровод трансформатора во время короткого замыкания не насыщен, поскольку поток взаимоиндукции Ф при коротком замыкании снижается почти вдвое из-за сильного размагничивающего действия токов вторичной обмотки (см. п. 5.2). Это допущение позволяет пренебречь током намагничивания и положить в основу расчета тока внезапного короткого замыкания упрощенную схему замещения (рис. 51). Процессы в этой схеме описываются линейным дифференциальным уравнением
 . (31)Решение данного уравнения имеет вид  . (32)Установившаяся составляющая 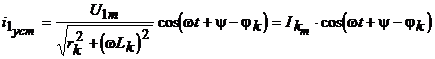 представляет собой частное решение уравнения (31): ,а свободная составляющая 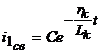 определяется из однородного дифференциального уравнения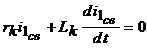 .Для нахождения постоянной интегрирования С зададим начальные условия в момент возникновения короткого замыкания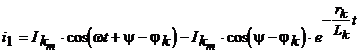:  . Подставляя это условие в (32), получим .Отсюда  . С учетом полученных соотношений выражение для тока короткого замыкания можно представить в виде . (33)Выражение (33) показывает, что свободная составляющая тока короткого замыкания имеет максимальное значение при  и  . При этих условиях ударное значение тока короткого замыкания  почти в два раза превышает его установившееся значение.
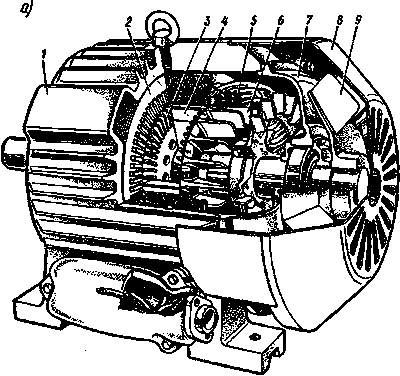
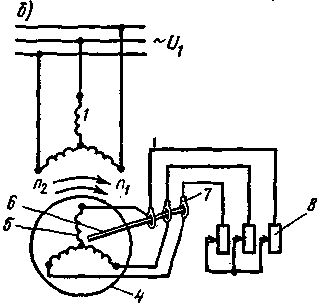
Изменение тока 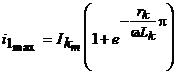 для случая показано на рис. 5 Ток 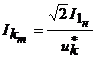короткого замыкания достигает максимального значения через полпериода после начала аварии, .Ток  можно выразить через напряжение короткого замыкания трансформатора, ,а коэффициент затухания 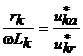 через его составляющие, .Для силовых трансформаторов  ;  . При этих параметрах максимальный ток короткого замыкания может достигать значений  .17.Элементы обмоток машин переменного тока Элементом обмотки является виток, состоящий из двух последовательно соединенных проводников, расположенных в пазах на расстоянии, приблизительно равном полюсному делению т. Группа витков, соединенных менаду собой и имеющих общую изоляцию от сердечника, называется катушкой. Одновитковая катушка обычно выполняется из проводников большого сечения, которые называются стержнями. Независимо от количества витков в катушке она имеет только две активные стороны, уложенные в пазы на расстоянии шага у обмотки. На схеме каждая сторона катушки изображается одной линией. 18.Магнитодвижущая сила обмоток машин переменного тока Магнитодвижущая сила (МДС) всех обмоток переменного тока, расположенных на статоре или роторе электрической машины, должна создавать в ее воздушном зазоре вращающееся магнитное поле. Для этого каждая из обмоток, питающаяся от синусоидально изменяющегося напряжения, должна иметь МДС, синусоидально распределенную в пространстве, т. е. по расточке статора или по окружности ротора. Несоблюдение этих условий, т. е. питание от несинусоидального напряжения или несинусоидальное распределение МДС приводит к появлению высших гармонических в кривой распределения магнитного потока, что ведет к ухудшению энергетических показателей машины. Для установления величины и характера распределения МДС обмотки сначала рассмотрим двухполюсную машину с простейшей сосредоточенной обмоткой (рис. 3.8, а), у которой все витки, включенные в фазу АХ, находятся в пазах, расположенных в диаметральной плоскости. При прохождении тока от начала фазы А к ее концу X возникает двухполюсный магнитный поток, силовые линии которого направлены, как показано на рисунке. Каждая силовая линия этого потока сцеплена со всеми витками w катушки данной фазы, поэтому создаваемая катушкой МДС Fк =∑i = iw. При максимальном значении тока в катушке эта МДС также имеет максимальное значение: Fкm=Imw= = √2Iw. 19.Вращающееся магнитное поле в электрических машинах переменного тока При питании однофазной обмотки переменным током возникает магнитное поле, пульсирующее во времени с частотой изменения тока. В этом случае при синусоидальном распределении МДС (рис. 3.12) в каждой точке воздушного зазора, расположенной на расстоянии х от оси обмотки, действует МДС (3.12) Fx = F0 cos (πx/τ) = Fm sin ωt cos (πx/τ), где F0 = Fm sin ωt - МДС в точке, расположенной на оси обмотки. Выражение (3.14) можно преобразовать к виду (3.13) Fx = 0,5Fm sin (ωt - πx/τ) + 0,5Fm sin (ωt + πx/τ). Каждый из членов правой части (3.13) представляет собой уравнение бегущей (или вращающейся) волны МДС. Следовательно, пульсирующее магнитное поле, синусоидально распределенное в пространстве, можно представить в виде суммы двух магнитных полей, вращающихся в противоположных направлениях (рис. 3.13). При этом бегущие волны МДС, создающие эти магнитные поля, (3.14) F'x = 0,5Fm sin (ωt - πx/τ); F''x = 0,5Fm sin (ωt + πx/τ). 20.Конструкция асинхронных машин с короткозамкнутым и с фазным ротором Двигатели с короткозамкнутым ротором (рис. 4.3, а и б). На статоре расположена трехфазная обмотка (см. § 3.6), которая при подключении к сети трехфазного тока создает вращающееся магнитное поле. Обмотка ротора выполнена в виде беличьей клетки, является короткозамкнутой и никаких выводов не имеет (рис. 4.3, в). Беличья клетка состоит из медных или алюминиевых стержней, замкнутых накоротко с торцов двумя кольцами (рис. 4.4, а). Стержни этой обмотки вставляют в пазы сердечника ротора без какой-либо изоляции. В двигателях малой и средней мощности беличью клетку обычно получают путем заливки расплавленного алюминиевого сплава в пазы сердечника ротора (рис. 4.4,6). Вместе со стержнями беличьей клетки отливают короткозамыкающие кольца и торцовые лопасти, осуществляющие вентиляцию машины.
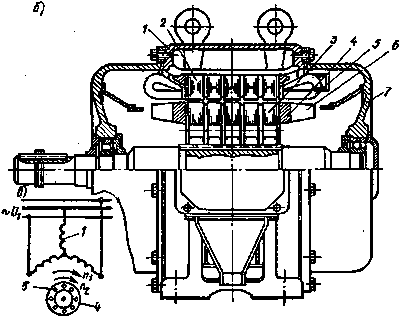
Для этой цели особенно пригоден алюминий, так как он обладает малой плотностью, легкоплавкостью и достаточно высокой электропроводностью. В машинах большой мощности пазы короткозамкнутого ротора выполняют полузакрытыми, в машинах малой мощности - закрытыми. Обе формы паза позволяют хорошо укрепить проводники обмотки ротора, хотя и несколько увеличивают потоки рассеяния и индуктивное сопротивление роторной обмотки. В двигателях большой мощности беличью клетку выполняют из медных стержней, концы которых вваривают в короткозамыкающие кольца (рис. 4.4, в). Различные формы пазов ротора показаны на рис. 4.4, г. В электрическом отношении беличья клетка представляет собой многофазную обмотку, соединенную по схеме Υ и замкнутую накоротко. Число фаз обмотки m2 равно числу пазов ротора z2, причем в каждую «фазу» входят один стержень и прилегающие к нему участки короткозамыкающих колец. Часто асинхронные двигатели с фазным и короткозамкнутым ротором имеют скошенные пазы на статоре или роторе. Скос пазов делают для того, чтобы уменьшить высшие гармонические ЭДС, вызванные пульсациями магнитного потока из-за наличия зубцов, снизить шум, вызываемый магнитными причинами, и устранить явление прилипания ротора к статору, которое иногда наблюдается в микродвигателях. Двигатели с фазным ротором (рис. 4.5, а). Обмотка статора выполнена так же, как и в двигателях с короткозамкнутым ротором. Ротор имеет трехфазную обмотку с тем же числом полюсов. Обмотку ротора обычно соединяют по схеме Υ, три конца которой выводят к трем контактным кольцам (рис. 4.5,6), вращающимся вместе с валом машины. С помощью металлографитных щеток, скользящих по контактным кольцам, в ротор включают пусковой или пускорегулирующий реостат, т. е. в каждую фазу ротора вводят добавочное активное сопротивление.
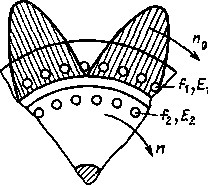
Чтобы уменьшить износ колец и щеток, двигатели с фазным ротором иногда имеют приспособления для подъема щеток и замыкания колец накоротко после выключения реостата. Однако введение этих приспособлений усложняет конструкцию электродвигателя и несколько снижает надежность его работы, поэтому обычно применяют конструкции, в которых щетки постоянно соприкасаются с контактными кольцами. Основные конструктивные элементы двигателя с фазным ротором приведены на рис. 4.6. 21.Частота ЭДС и токов в обмотке статора и ротора асинхронной машины. Скольжение. Из выражения (10.11) следует, что частота тока статора пропорциональна частоте вращения магнитного поля, созданного током статора: (10.20) f1 = n0p/60. Так как ротор вращается в сторону поля (рис. 10.14), частота пересечения его обмотки магнитным полем будет определяться разностью частот вращения магнитного поля и ротора. По аналогии с (10.20) частота тока ротора (10.21) f2 = (n0 - n)р/60. Из отношения (10.20) к (10.21) f1/f2 = n/(n0 - n) получаем выражение частоты тока ротора (10.22) f2 = f1 (n0 - n)/n0 = f1s, где s — скольжение: (10.23) s = (n0 - n)/n0. Скольжение — величина безразмерная, представляющая собой частоту вращения ротора относительно поля статора, выраженную в долях частоты вращения поля статора. Когда ротор неподвижен (n = 0),
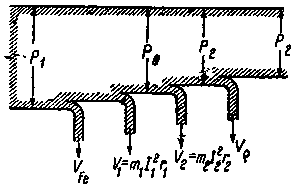
s = (n0 - 0)/n0 = 1; f2 = f1s = f1 • 1 = f1. Если ротор вращается с частотой поля, то s = (n0 - n0)/n0 = 0; f2 = f1s = f2 • 0 = 0. При неподвижном роторе его обмотка относительно поля находится в тех же условиях, что и обмотка статора. Поэтому ЭДС обмотки ротора может быть определена по аналогичной формуле, что и ЭДС обмотки статора: (10.24) E2к = 4,44f1w2Фk02, где w2 — число витков фазы обмотки ротора k02 — обмоточный коэффициент обмотки ротора. Когда ротор вращается, (10.25) Е2 = 4,44f2w2Фk02. Из отношения (10.24) и (10.25) вытекает, что (10.26) E2 = E2к = f2/f1. Подставив в (10.26) вместо f2 его значение из (10.22), получим (10.27) E2 = E2k = f1s/f1 = E2ks. Таким образом, ЭДС обмотки ротора пропорциональна скольжению. При n = 0 s = 1, E2 = E2к; при n = n0 s = 0, E2 = 0. 23. уравнение напряжение статора и ротора АМ Обмотка ротора асинхронного двигателя не имеет электрической связи с обмоткой статора. Между ними существует только магнитная связь и энергия из обмотки статора передается в обмотку ротора магнитным полем. В этом отношении асинхронная машина аналогична двухобмоточному трансформатору: обмотка статора является первичной, а обмотка ротора - вторичной. Так же как и в трансформаторе, в асинхронной машине имеется результирующий магнитный поток Ф, сцепленный как с обмоткой статора, так и с обмоткой ротора, и два потока рассеяния:  - поток рассеяния обмотки статора и  - поток рассеяния обмотки ротора.Амплитуда результирующего магнитного потока  , вращающегося с частотой n1, наводит в фазах неподвижной обмотки статора ЭДС, действующее значение которой равно .Магнитный поток рассеяния наводит в фазах обмотки статора ЭДС рассеяния, значение которой определяется падением напряжения на индуктивном сопротивлении рассеяния фазы обмотки статора ,где  - индуктивное сопротивление рассеяния фазы обмотки статора.Уравнение напряжения фазы обмотки статора, включенной в сеть с напряжением  , запишется: ,где  - падение напряжения на активном сопротивлении фазы обмотки статора  .Окончательная запись уравнения не отличается от уравнения напряжения для первичной обмотки трансформатора .Результирующий магнитный поток Ф, обгоняя вращающийся ротор, индуктирует в фазе обмотки ротора ЭДС  где  - частота ЭДС  в фазе обмотки вращающегося ротора;  - ЭДС, наведенная в фазе обмотки неподвижного ротора.Магнитный поток рассеяния наводит в фазах обмотки ротора ЭДС рассеяния, значение которой определяется падением напряжения на индуктивном сопротивлении фазы этой обмотки: ,где  - индуктивное сопротивление рассеяния фазы обмотки ротора при неподвижном роторе.Уравнение напряжения для фазы обмотки ротора  ,где  - активное сопротивление фазы обмотки ротора.Окончательная запись уравнения:  .24.Схема замещения АМ При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентной схемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора. По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r2'(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Zн. Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания. 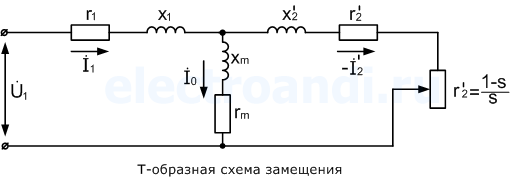 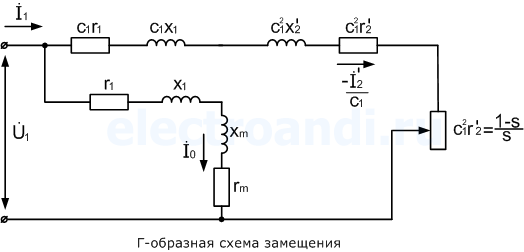 В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c1, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.  Величина c1 приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c1≈1. При этом следует учитывать, что значение коэффициента c1 уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю. Другой источник Для расчета характеристик асинхронного двигателя и исследования различных режимов его работы удобно использовать схемы замещения. При этом реальная асинхронная машина с электромагнитными связями между обмотками заменяется относительно простой электрической цепью, что позволяет существенно упростить расчет характеристик. С учетом того, что основные уравнения асинхронного двигателя (2.25) аналогичны таким же уравнениям трансформатора (1.23), схема замещения двигателя такая же, как и у трансформатора, представлена она на рисунке 2.6. 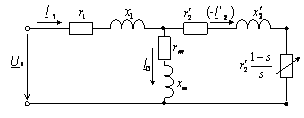  Рисунок 2.6 – T-образная схема замещения асинхронного двигателя Изображенная на рисунке 2.6 схема называется T-образной схемой замещения (сопротивления  ,  и  образуют букву Т), в ней: r1 и x1– активное и индуктивное сопротивления фазной обмотки статора;  и  – при-веденные активное и индуктивное сопротивления фазной обмотки ротора.Сопротивление  определяет параметры намагничивающей ветви схемы. Индуктивная составляющая  является индуктивным сопротивлением взаимной индукции. Посредством сопротивления  учитываются магнитные потери в стали статора  . Как и в трансформаторе, сопротивление зависит от подведенного напряжения U1. С повышением U1 сопротивление уменьшается.При расчете характеристик асинхронного двигателя с использованием схемы замещения ее параметры должны быть известны. Схема рисунка 2.6 полностью отражает физические процессы, происходящие в двигателе, но имеет узловую точку между сопротивлениями 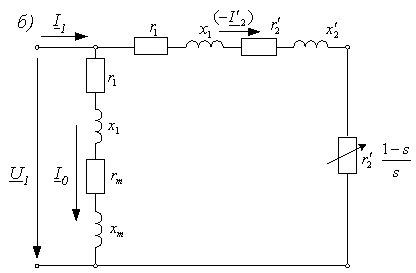и , что усложняет расчет токов при различных значениях скольжения. Поэтому большое практическое применение для анализа режимов работы асинхронных машин находит другая схема замещения, в которой намагничивающая ветвь подключена непосредственно на входе схемы, куда подводится напряжение U1 (рисунок 2.7). Данная схема называется Г-образной схемой замещения.  Рисунок 2.7 – Г-образная схема замещения асинхронного двигателя (а) и ее упрощенный вариант (б) На рисунке 2.7, а комплексный коэффициент  или  .Так как x1 >> xm, то  незначительно больше единицы ( ).Если пренебречь коэффициентом  , то получим упрощенную Г-образную схему замещения (рисунок 2.7, б), которую используют при практических расчетах асинхронных двигателей средних и больших мощностей. При этом погрешность в расчете не превышает 1–5%.Необходимость учета коэффициента возникает главным образом при анализе асинхронных двигателей небольшой мощности.Согласно (2.22) активное сопротивление обмотки ротора двигателя разбито на две части:   . Первое сопротивление не зависит от режима работы, и потери в нем равны электрическим потерям реального ротора. Второе сопротивление зависит от скольжения, и мощность, выделяемая в нем, численно равна механической мощности двигателя Рмех. Следовательно сопротивление  в схеме замещения выполняет роль нагрузки двигателя.Из упрощенной Г-образной схемы замещения можно определить приведенный ток роторной обмотки 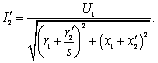 . (2.26)В дальнейшем (2.26) используется при выводе уравнения электромагнитного момента асинхронного двигателя. 25. энергетическая диаграмма асинхронного двигателя Все преобразования энергии и потери, которые происходят в асинхронном двигателе, можно иллюстрировать при посредстве так называемой "энергетической" диаграммы. На фиг. 88 показана такая диаграмма в форме "потока энергии", который течет слева направо. Как видно из фиг. 88, этот "поток" состоит из ряда "рукавов". Притекающая к статору асинхронного двигателя из сети электрическая энергия Р1 изображена на фиг. 88 в виде потока наибольшей ширины. По мере течения направо главное "русло" этого потока делается все уже и уже. "Рукав" потока VFe изображает потери железа в двигателе (токи Фуко и гистерезис). Рукав потока V1 = m1I12• r1 изображает потери меди в статоре. Потери меди в роторе m2 • I22 • r2 изображены рукавом потока V2 и, наконец, рукав потока Vρ изображает механические потери. Таким образом притекающая к статору мощность Р1 оказывается больше тормозной мощности двигателя Р2 на величину суммарных потерь фиг. 88. На диаграмме фиг. 88, кроме того, очень наглядно представлены весьма характерные в теории асинхронных двигателей величины мощности Р'2 и Ps.
а) Мощность Р'2 есть мощность ротора; эта мощность меньше мощности, подведенной к статору, на величину суммы потерь VFe + V1 + V2; если из мощности ротора Р2 вычесть мощность, соответствующую механическим потерям Vρ, то получится мощность на валу двигателя W2. b) Мощность Ps носит обычно название мощности вращающегося потока; Ps равно сетевой мощности Р1 за вычетом суммарных потерь в статоре VFe + V1. Мощность Ps является, как будет видно ниже, весьма характерной величиной в теории асинхронных двигателей. 25.вопрос Энергетическая диаграмма асинхронного двигателя Энергетическая диаграмма позволяет судить о характере распределения мощности, потребляемой двигателем из сети. Ее можно получить с помощью векторной диаграммы (рис.4.9). При работе асинхронный двигатель потребляет из сети активную мощность  .Из векторной диаграммы можно получить следующие соотношения: 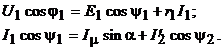 С учетом этих соотношений выражение для мощности  преобразуется к виду .Отсюда следует, что мощность расходуется в статоре на покрытие электрических потерь в обмотке статора, и на покрытие потерь в стали,  .Остальная мощность поступает через воздушный зазор в ротор. Эта мощность определяет электромагнитный момент двигателя, поэтому ее называют электромагнитной мощностью  .Из векторной диаграммы можно получить следующее соотношение:  ,поэтому для электромагнитной мощности справедливо второе выражение:  . | |||||||||||||||||||
