233609 фин. м-ка. Контрольная работа 1 2 Задача 1 2 Задача 2 3 Задача 3 4 Задача 4 4 Задача 5 5 Контрольная работа 2 5 Задача 1 5 Задача 2 6

• Название: Контрольная работа 1 2 Задача 1 2 Задача 2 3 Задача 3 4 Задача 4 4 Задача 5 5 Контрольная работа 2 5 Задача 1 5 Задача 2 6
• Дата: 28.09.2022
• Размер: 98.52 Kb.
• Имя файла: 233609 фин. м-ка.docx
• Тип: Контрольная работа; #703815

Содержание

Контрольная работа 1 2

Задача 1 2

Задача 2 3

Задача 3 4

Задача 4 4

Задача 5 5

Контрольная работа 2 5

Задача 1 5

Задача 2 6

Задача 3 7

Задача 4 7

Задача 5 8

Контрольная работа 3 9

Задача 1 9

Задача 2 10

Задача 3 11

Задача 4 12

Задача 5 13

Контрольная работа 4 14

Задача 1 14

Задача 2 15

Задача 3 16

Задача 4 17

Контрольная работа 5 19

Кейс 3. Определение наращенной суммы на конец срока 19

Список использованных источников 24

Контрольная работа 1

Задача 1

Условие:

Кредит в размере 270 тыс. р. выдан под сложную пpoцентную ставку 2,2% в месяц сроком на один год. Определите полную сумму долга к концу срока.
Решение:

Сумму долга к концу срока определим по формуле.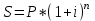

,

где S - наращенная по сложным процентам сумма,

Р - основной капитал,

i - процентная ставка за период,

n — срок (в периодах, соответствующих процентной ставке).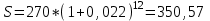

тыс. руб.
Ответ: S=350,57 тыс. руб.

Задача 2

Условие:

Определите сумму сложных процентов, начисленных на долг  в размере 90 тыс, р., выданный на 1 год и 3 месяца, если проценты начисляются ежеквартально по ставке 6,5% в квартал.
Решение:

Наращенную сумму определим по формуле.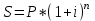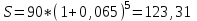



тыс. руб.

Сумма процентов: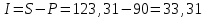

тыс. руб.
Ответ: I=33,31 тыс. руб.

Задача 3

Условие:

Проценты по ссуде размером 5 тыс. р., выданной на два месяца, составили 125 р. Какова процентная ставка?
Решение:

P=5000 руб, I=125 руб, Т=2/12

Зная, что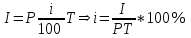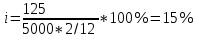


Ответ: годовая процентная ставка – 15%.

Задача 4

Условие:

Банк выплачивает 63,75 долл. каждые полгода по валютному вкладу исходя из простой годовой процентной ставки 6 %. Определите сумму вклада.

Решение:

I=63,75 долл, i=6% годовых, Т=1/2

Зная, что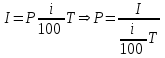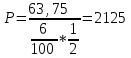

долл.
Ответ: Р=2125 долл

Задача 5

Условие:

Срочный вклад в размере 150 тыс. р. размещен в коммерческом банке на шесть лет. При этом простая годовая процентная ставка в течение первых трех лет составляет 10 %, следующие два года она увеличивается до 15%, а в течение последнего года составляет 20 % годовых. Определите наращенную сумму денег на вкладе.
Решение:

Наращенную сумму по ставке простых процентов найдем по формуле 2.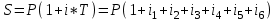



i₁=i₂=i₃=10%=0,1

i₄=i₅=15%=0,15

i₆=20%=0,2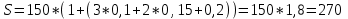

тыс. руб.
Ответ: S=270 тыс. руб.

Контрольная работа 2

Задача 1

Условие:

Определите значение простой годовой процентной ставки, эквивалентной простой годовой учетной ставке 16%, для финансовой операции сроком на 2 месяца.
Решение:

Для нахождения простой годовой процентной ставки воспользуемся формулой.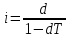



d=16%=0,16

T=2/12=1/6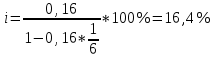


Ответ: i=16,4%

Задача 2

Условие:

Два векселя на сумму 10 тыс. и 20 тыс. р. со сроками погашения 10 июня и 1 августа соответственно заменяют одним векселем с продлением срока до 1 октября. Определите сумму нового векселя, если при объединении применена простая годовая учетная ставка 8 %.
Решение:

Поскольку срок погашения нового векселя позже, чем сроки погашения объединяемых векселей, то на сумму 10 000 руб. в течении 113 дней (с 10 июня по 1 октября) происходит наращение капитала по простой учетной ставке 8%; на сумму 20 000 руб. в течении 61 дней (с 1 августа по 1 октября) также происходит наращение капитала по простой учетной ставке 8% годовых. Тогда сумму нового векселя определим по формуле.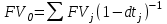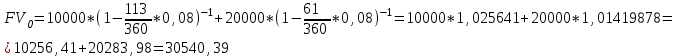




Ответ: FV₀=30540,39 руб.

Задача 3

Условие:

Ссуда в размере 350 тыс. р. выдана под проценты на 3 года с условием возврата в конце срока 470 тыс. р. Определите доходность этой операции в виде сложной годовой процентной ставки.
Решение:

Сложную годовую процентную ставку можно определить по формуле.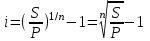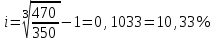




Ответ: i=10,33 %

Задача 4

Условие:

Заемщик получил сроком на 9 месяцев ссуду на следующих условиях: наращение процентных денег проводится по схеме простых процентов, причем за первый квартал годовая процентная ставка равна 18 %, а каждый последующий квартал она повышается на 2 %. Оцените доходность ссудной операции на основе средней процентной ставки.
Решение:

Среднюю процентную ставку рассчитаем по формуле.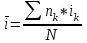



n₁=n₂=n₃=1/4=0,25

i₁=18%=0,18; i₂=20%=0,2; i₃=22%=0,22

N=3*0,25=0,75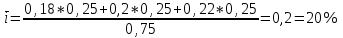


Ответ: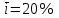

Задача 5

Условие:

Цены ежемесячно увеличиваются на 0,8 %. Определите годовой темп инфляции.
Решение:

Рассчитаем годовой темп инфляции: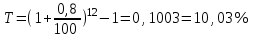


Ответ: Т=10,03 %

Контрольная работа 3

Задача 1

Условие:

Необходимо найти наращенную сумму ренты постнумерандо с годовым платежом 10 тыс. р. при условии, что проценты начисляют поквартально по номинальной ставке 14 % годовых. Срок ренты — 8 лет.
Решение:

Наращенную сумму найдем по формуле: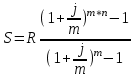



R=10 тыс. руб., j=14%, n=8 лет, m=4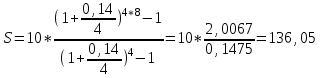

тыс. руб.
Ответ: S=136,05 тыс. руб.

Задача 2

Условие:

Фирма собирается учредить фонд для ежегодной (в конце года) выплаты пособий своим работникам. Определите сумму, которую фирма должна для каждого работника поместить на депозит    в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 30 тыс. р., если банк начисляет сложные проценты по ставке 18 % годовых: а) ежегодно; б) ежеквартально; в) ежемесячно.
Решение:

Денежный поток во всех случаях является бессрочным аннуитетом постнумерандо, причем А=30 тыс. руб. Необходимо найти приведенную стоимость этого аннуитета.

а) при ежегодном начислении процентов: r=18%=0,18, p=m=1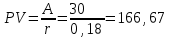

тыс. руб.

б) при ежеквартальном начислении: r=18%=0,18, p=1, m=4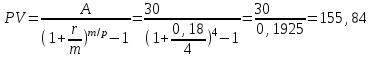

тыс. руб.

в) при ежемесячном начислении: r=18%=0,18, p=1, m=12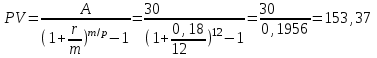

тыс. руб.
Ответ: а) PV=166,67 тыс. руб; б) PV=155,84 тыс. руб; в) PV=153,37 тыс. руб.

Задача 3

Условие:

Для замены оборудования через 5 лет предприятию потребуется 10 млн р. Предприятие создает целевой фонд для накопления этих средств. Определите размер ежемесячного платежа в целевой фонд, если банк ежеквартально начисляет на вложенные средства сложные проценты по ставке 12 % годовых.

Решение:

Из формулы наращенной суммы ренты постнумерандо, выразим ежемесячный платеж: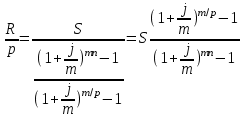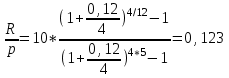



млн. руб.=123 тыс. руб.
Ответ: 123 тыс. руб.

Задача 4

Условие:

Необходимо годовую ренту пренумерандо со сроком 3 года равным платежом, составляющим 1 000 тыс. р., и годовой процентной ставкой 9 % заменить на ренту постнумерандо со сроком 5 лет с той же процентной ставкой.
Решение:

Наращенная стоимость первой ренты пренумерандо определяется по формуле: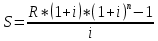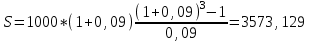



тыс.руб.

Наращенная стоимость ренты постнумерандо определяется по формуле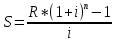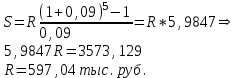




Ответ: R=597,04 тыс. руб.

Задача 5

Условие:

Товар стоимостью 25 тыс. р. продают в кредит на 2 года под простую годовую процентную ставку 16 % с равными ежеквартальными выплатами. Определите сумму долга с процентами и размер ежеквартального платежа. С помощью «правила 78» составьте план погашения кредита.
Решение:

По формуле наращения по простым процентам: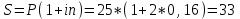

тыс. руб.

Величину выплаченных процентов определим по формуле:

I=S-P=33-25=8 тыс. руб.

Величину разового платежа определим по формуле: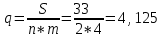

тыс. руб.

Составим план выплат с помощью "правила 78". Так как запланировано к = 2 *4 = 8 платежей, Находим сум­му порядковых номеров всех платежей: 1+2 + 3 +4 + 5 + 6 +7+8= 36. Согласно "правилу 78" часть первого погасительного платежа пойдет на выплату 8/36 от общей начисленной величины процентов, оставшаяся часть погасительного платежа (а- 8/36)пойдет в счет выплаты основного долга. Часть второго погасительного платежа пойдет на выплату 7/36 от общей начисленной величины процентов, а оставшаяся часть платежа (а- 7/36) пойдет в счет выплаты основного долга, и т.д.

В таблице 1 приведены результаты вычислений.
Таблица 1 – Результат вычислений по правилу 78

Номер квартала	Остаток основного долга на начало квартала, тыс. руб.	Дробь	Погашение общей величины начисленных процентов, тыс. руб.	Погашение основного долга, тыс. руб.
1	25	8/36	1,778	4,125-1,778=2,347
2	25-2,347=22,653	7/36	1,556	2,569
3	20,084	6/36	1,333	2,792
4	17,292	5/36	1,111	3,014
5	14,278	4/36	0,889	3,236
6	11,042	3/36	0,667	3,458
7	7,584	2/36	0,444	3,681
8	3,903	1/36	0,222	3,903
Итого		1	8	25

Ответ: S=33 тыс. руб.; I=8 тыс. руб.; q=4,125 тыс. руб.

Контрольная работа 4

Задача 1

Условие:

Ссуда в размере 50 тыс. р. была выдана на 7 месяцев под простую обыкновенную годовую процентную ставку 10%. Сколько должен выплатить должник, если долг погашают в конце периода одним платежом?
Решение:

Погашаемую сумму определим по формуле: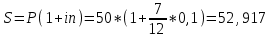

тыс. руб.
Ответ: S=52,917 тыс. руб.

Задача 2

Условие:

Предприниматель получил кредит на 5 лет на сумму 1 000 тыс. р. под сложную годовую процентную ставку 20%, начисляемую ежегодно на непогашенный остаток. В соответствии с финансовым соглашением предприниматель будет погашать основной долг равными суммами. Определите размеры срочных выплат при ежегодном погашении кредита, а также при выплате долга с процентами в конце срока. Какой вариант предпочтительнее для заемщика?

Решение:

Расчет периодического платежа при ежегодном погашении кредита осуществляется по формуле.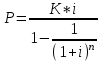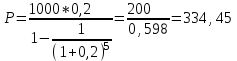



тыс. руб.

Общие расходы заемщика по погашению кредита составят: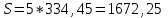

тыс. руб.

При выплате долга с процентами в конце срока сумма составит: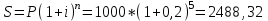

тыс. руб.

Для заемщика предпочтительнее первый вариант, при ежегодном погашении кредита.
Ответ: 1672,25 тыс. руб; 2488,32 тыс. руб.

Задача 3

Условие:

Ссуда в размере 2 500 тыс. р. предоставлена фирме на пятилетний срок. Проценты на долг начисляют по сложной годовой процентной ставке 18%. Для погашения ссуды образован погасительный фонд, поскольку имеется возможность поместить средства под сложную годовую процентную ставку 21 %. Определите размер годового платежа в погасительный фонд.
Решение:

Для того, чтобы погасить долг с процентами, необходимо к концу срока накопить в фонде следующую сумму: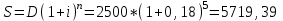

тыс. руб.

Для того, чтобы определить размер ежегодного платежа в накопительный фонд, составим следующее уравнение: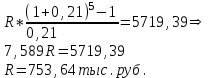


Ответ: R=753,64 тыс. руб.

Задача 4

Условие:

Предприятие рассматривает целесообразность приобретения новой технологической линии по цене 17 000 тыс. р. По прогнозам, сразу после пуска линии ежегодные поступления после вычета налогов составят 5 700 тыс. р. Работа линии рассчитана на 5 лет. Ликвидационная стоимость линии равна затратам на ее демонтаж. Необходимая норма прибыли составляет 12 %. Определите чистый приведенный доход проекта:

а) при отсутствии инфляции;

б) при условии, что на предстоящий период прогнозируется

среднегодовой уровень инфляции 9 %.
Решение:

Чистая текущая стоимость проекта при отсутствии инфляции: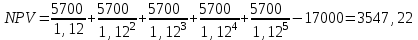

тыс. руб.

Так как чистый приведенный доход положительный, то проект следет принять.

С учетом инфляции требуемая норма доходности должна составить г = (1+0,09)*(1+0,12)-1=22,08%

Чистая текущая стоимость проекта с учетом инфляции: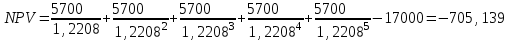

тыс. руб.

В данном случае проект следует отвергнуть, так как чистый приведенный доход отрицательный.
Ответ: а) 3547,22 тыс. руб.; б) -705,139 тыс. руб.

Контрольная работа 5

Кейс 3. Определение наращенной суммы на конец срока

Условие:

1. Ситуация:

В фонд компанией «СМАРТ» ежегодно вносится по 10 000 руб. в течение 20 лет. Платежи производят равными долями в конце каждого квартала. Сложные проценты по ставке 10 % годовых начисляются один раз в конце года.

2. Проблема указанной ситуации состоит в необходимости определения наращенной суммы на конец срока с наименьшими убытками и рисками.

Ключевое задание.

1) Предложите различные способы решения поставленной задачи.

2) Выберите оптимальный способ решения.

3) Выведите формулу нахождения наращенной суммы на конец срока.

3. Детальное исследование ситуации в зависимости от поставленных задач.

1) Какому значению будет равна наращенная сумма на конец срока, если сложные проценты по ставке 10 % годовых будут начисляться ежеквартально?

2) Какие изменения произойдут в формуле подсчета наращенной суммы, если сложные проценты будут начисляться ежеквартально?

3) Какому значению будет равна наращенная сумма на конец срока, если сложные проценты по ставке 10 % годовых будут начисляться в конце каждого месяца?

4) Какие изменения произойдут в формуле подсчета наращенной суммы, если сложные проценты будут начисляться в конце каждого месяца?

 

Решение:

1) Предложите различные способы решения поставленной задачи.

В нашем случае имеем поток одинаковых платежей через одинаковые промежутки времени.

Первый способ – это найти наращенную сумму каждого платежа и сложить их. Т.к. всего будет 4 * 20 = 80 платежей, то процесс чрезвычайно трудоемкий (даже с использованием функций Эксель).

Второй способ – это найти наращенную сумму годовых платежей (их можно суммировать, т.к. проценты начисляются раз в год), но все равно будет 20 расчетов.

Третий способ - применить формулу наращенной суммы р-срочной ренты с годовым начислением процентов.
2) Выберите оптимальный способ решения.

Оптимальным и менее трудоемким является третий способ.
3) Выведите формулу нахождения наращенной суммы на конец срока.

Формулы уже выведены и представлены в учебных пособиях для разных случаев.

Для исходного задания берем формулу наращенной суммы если рентные платежи вносятся m раз в году равными суммами (р-срочная рента), а проценты на них начисляются раз в году равна :

S = R *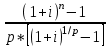

Где S – наращенная сумма,

R – величина ежегодного взноса,

i – процентная ставка,

р – число рентных платежей в году

n – срок ренты.

S = 100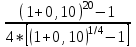00 * = 10000 * 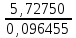= 593801,71 руб.
3. Детальное исследование ситуации в зависимости от поставленных задач.
Так как внутренние параметры уже определены – это четыре квартальных платежа на общую сумму 10000 руб., то возможно улучшение вложения и увеличение наращенной суммы с помощью поиска лучшего внешнего условия фонда. Фонд может заинтересовать клиента частотой начисления процентов, что как мы знаем должно повысить эффективную годовую ставку.

1. 
   Какому значению будет равна наращенная сумма на конец срока, если сложные проценты по ставке 10 % годовых будут начисляться ежеквартально?
   

В данном случае рентные платежи вносятся несколько раз в году (р-срочная рента), начисление процентов производится m раз в году, число периодов начисления процентов в течении года равно числу рентных платежей в течении года, т.е. m = р.

В этом случае наращенная сумма определяется по формуле :

S = R *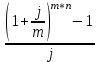

S – наращенная сумма,

R – сумма рентных платежей в год,

j – номинальная ставка процентов,

m – число периодов начисления процентов в течении года,

n – срок ренты в годах

S = 100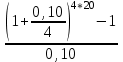00 * = 10000 * 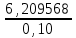= 620956,78 руб.

2. 
   Какие изменения произойдут в формуле подсчета наращенной суммы, если сложные проценты будут начисляться ежеквартально?
   

В числителе дроби ставка стала делиться на 4 квартала, но и число периодов начисления процентов (степень) также увеличилось в 4 раза.

В знаменателе дроби с помощью степени стали (и последующего вычитания единицы) стали выходить на эффективную квартальную ставку и потом умножать ее на 4 (число кварталов).

3. 
   Какому значению будет равна наращенная сумма на конец срока, если сложные проценты по ставке 10 % годовых будут начисляться в конце каждого месяца?
   

В этом случае рентные платежи вносятся несколько раз в году и начисление процентов несколько раз в году, но число рентных платежей в течении года не равно числу периодов начисления процентов, т.е. m≠p.

S = R *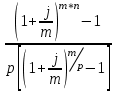

Где S – наращенная сумма,

R – величина ежегодного взноса,

j – годовая процентная ставка,

n – срок ренты в годах.

m – число периодов начисления процентов в течении года.

p – количество выплат в год
S = 10000 * 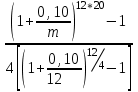= 627563,14 руб.

4. 
   Какие изменения произойдут в формуле подсчета наращенной суммы, если сложные проценты будут начисляться в конце каждого месяца?
   

В числителе дроби ставка стала делиться на 12 месяцев, но и число периодов начисления процентов (степень) также увеличилось в 12 раз.

В знаменателе дроби сначала определяется месячная номинальная ставка путем деления на 12, потом с помощью степени и учета отношения числа месяцев в квартале (и последующего вычитания единицы) стали выходить на эффективную квартальную ставку и потом умножать ее на 4 (число кварталов).
ВЫВОД : Расчеты эффективнее вести по специальным формулам.

Если есть возможность, то выгоднее будет вкладывать в фонд, который чаще начисляет проценты. В этом случае наращенная сумма будет больше.

Список использованных источников

1. 
   Брусов, П.Н. Финансовая математика: Учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова. - М.: КноРус, 2013. - 224 c.
   
2. 
   Касимов, Ю.Ф. Финансовая математика: Учебник и практикум для бакалавриата и магистратуры / Ю.Ф. Касимов. - Люберцы: Юрайт, 2016. - 459 c.
   
3. 
   Малыхин, В.И. Финансовая математика / В.И. Малыхин. - М.: Ленанд, 2015. - 232 c.
   
4. 
   Малько, А.В. Финансовая математика (для бакалавров) / А.В. Малько, В.В. Нырков, К.В Шундиков. - М.: КноРус, 2013. - 224 c.
   
5. 
   Саркисов, А.С. Финансовая математика: ТЕОРИЯ ПРОЦЕНТОВ в задачах и упражнениях. Около 500 примеров и тренировочных задач / А.С. Саркисов. - М.: Ленанд, 2016. - 304 c.