Контрольная Работа Модуль 1 (2). Контрольная работа 1 Написать ответы на вопросы
 Скачать 45.11 Kb. Скачать 45.11 Kb.
|
|
Контрольная работа №1 Написать ответы на вопросы: Искусственные липидные мембраны. Липосомы. Применение липосом в медицине. Модельные мембраны Изучение физических свойств липидного слоя мембран осуществляется преимущественно на двух видах искусственных мембранных структур, образованных синтетическими фосфолипидами или липидами, выделенными из биологических источников: липосомах и бислойных липидных мембранах (БЛМ). Липосомы Липосомы – это липидные везикулы (пузырьки), образующиеся из фосфолипидов в водных растворах. Чтобы получить липосомы, спиртовый раствор фосфолипидов впрыскивают в большой объем водного раствора фосфолипиды, нерастворимые в воде, образуют мелкие пузырьки, стенки которых состоят из одного липидного бислой я (однослойные липосомы). Можно сначала высушить раствор фосфолипидов в органическом растворителе (например, хлороформе) в пробирке, добавить в пробирку водный раствор и хорошенько потрясти пробирку. Липиды переходят в водный раствор, теперь уже в виде многослойных липосом. Суспензию липосом обычно используют для изучения физических свойств липидного бислоя как вязкость, поверхностный заряд или диэлектрическая проницаемость, а также для изучения проницаемости для незаряженных молекул. Бислойные липидные мембраны (БЛМ) Для изучения ионной проницаемости липидного слоя мембран используют БЛМ. Для приготовления БЛМ в стаканчик с раствором электролита помещают второй, тефлоновый стаканчик , в стенке которого сделано отверстие, диаметром около 1 мм. С помощью капилляра в отверстие вводят маленькую каплю раствора фосфолипида в жидком углеводороде, гептане или гексане). Молекулы фосфолипидов собираются на поверхности капли таким образом, что полярные головки молекул обращены в водную среду, а гидрофобные хвосты – внутрь капли. Постепенно растворитель уходит из капли и улетучивается, а капля превращается в липидную пленку (БЛМ). В БЛМ полярные головки фосфолипидов обращены в водную фазу, а неполярные углеводородные цепи жирных кислот сливаются в сплошную вязкую фазу во внутренней части липидной мембраны. По многим свойствам эта пленка сходна с липидным слоем биологических мембран. В настоящее время это, пожалуй, наиболее активно развивающееся направление практического использования липосом. Способность липосом включать в себя самые разные вещества практически без каких-либо ограничений в отношении их химической природы, свойств и размера молекул дает поистине уникальные возможности для решения некоторых медицинских проблем. Так, многие лекарственные препараты имеют низкий терапевтический индекс. Это означает, что концентрация, в которой они оказывают лечебное действие, мало отличается от концентрации, при которой препарат становится токсичным. В других случаях лекарственный препарат при введении в организм может быстро терять активность под действием инактивирующих агентов. Включение таких препаратов в липосомы может значительно повысить их терапевтическую эффективность, поскольку, с одной стороны, препарат, находящийся в липосоме, защищен ее мембраной от действия неблагоприятных факторов, а с другой - та же мембрана не позволяет токсичному препарату превысить допустимую концентрацию в биологических жидкостях организма. Липосома в данном случае выполняет роль хранилища, из которого препарат высвобождается постепенно, в нужных дозах и в течение требуемого промежутка времени. С точки зрения биологической совместимости липосомы идеальны как переносчики лекарственных препаратов. Они делаются из природных липидов и поэтому нетоксичны, не вызывают нежелательных иммунных реакций и биодеградируемы, то есть должны разрушаться под действием обычных ферментов, присутствующих в организме. Однако ситуация с терапевтическим применением липосом не так проста, как хотелось бы. Оказалось, что липосомы недостаточно стабильны в крови и быстро выводятся из кровотока макрофагами, которые находятся в печени, селезенке и костном мозгу. По этой же причине липосомные носители обычно не удается направить именно в те органы и ткани, где происходит патологический процесс. Следует, однако, сказать, что привлекательность идеи липосомной терапии была настолько велика, что перечисленные осложнения стимулировали многочисленные и интенсивные исследования, в результате которых для многих проблем были найдены оригинальные, а порой и остроумные решения. Так, естественная нацеленность макрофагов на липосомы может быть использована для их активации, что очень полезно для борьбы с вирусными, бактериальными и грибковыми инфекциями. Тот факт, что липосомы не задерживаются такими органами, как сердце, почки, мозг, а также клетками нервной системы, позволяет за счет использования липосомных лекарственных форм значительно снизить кардиотоксичность, нефротоксичность и нейротоксичность ценных препаратов, применяемых для противораковой терапии. Кроме того, прикрепление к поверхности липосом молекул, специфичных по отношению к клеткам-мишеням (например, иммуноглобулинов), в некоторых случаях оказывается эффективным для направленной доставки противораковых, противоинфекционных и противовоспалительных препаратов. Проблема доставки лекарства в нужное место может быть также решена путем местного применения липосомных препаратов, как это было сделано в случае противоартритных препаратов, а также препаратов для лечения дыхательного синдрома новорожденных и астмы. Понятие и единицы измерения основных характеристик механической волны: длина волны, скорость волны, амплитуда и частота, период колебаний. Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне. Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне или звуковые волны в газе являются примерами таких волн. Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ. Смещение y (x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:
где k = 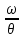 – так называемое волновое число, ω = 2πf – круговая частота. – так называемое волновое число, ω = 2πf – круговая частота.Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны. Для любой выбранной точки на графике волнового процесса с течением времени t изменяется координата x этой точки, а значение выражения ωt – kx не изменяется. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:
Отсюда следует:
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число k= 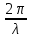 является пространственным аналогом круговой частоты является пространственным аналогом круговой частоты 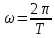 . .Обратим внимание на то, что уравнение
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью 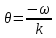 Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени. Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны. В зависимости от формы фронта волны различают волны плоские, сферические и др. В плоской волне волновые поверхности представляют собой плоскости, перпендикулярные к направлению распространения волны. Плоские волны можно получить на поверхности воды в плоской ванночке с помощью колебаний плоского стержня (рис. 1). Рис. 1. 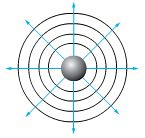 В сферической волне волновые поверхности представляют собой концентрические сферы. Сферическую волну может создать пульсирующий в однородной упругой среде шар. Такая волна распространяется с одинаковой скоростью по всем направлениям. Лучами являются радиусы сфер. Основными характеристиками волны: амплитуда (A) — модуль максимального смещения точек среды из положений равновесия при колебаниях; период (T) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны) T=t/N, где t — промежуток времени, в течение которого совершаются N колебаний; частота (ν) — число полных колебаний, совершаемых в данной точке в единицу времени ν=N/t Частота волны определяется частотой колебаний источника Дать ответы на тесты и занести в таблицу (тесты содержатся в пособии: Рабочая тетрадь по биофизике).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
