Главная страница
Навигация по странице:

  • Контрольная работа №1 «Построение факторной регрессионной модели.

  • ТЕОРИЯ: Методика построения факторной регрессионной модели

  • ЭТАП 1. Представление спецификаций факторной регрессионной модели.

  • ЭТАП 2. Идентификация параметров факторных регрессионных моделей. Цель

  • ЭТАП 3. Проверка значимости параметров регрессионной модели

  • ЭТАП 3. Проверка значимости модели регрессии.

  • ЭТАП 4. Оценка качества модели регрессии.

  • Модель (в явном виде) Информационные характеристики качества однофакторной модели s

  • ЭТАП 5. Анализ остаточной компоненты. Выполнение требований Гаусса-Маркова.

    		•

    Контрольная работа 1 Построение факторной регрессионной модели


    Скачать 119.22 Kb.
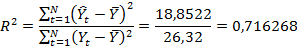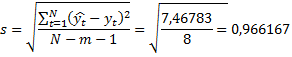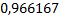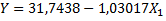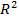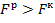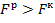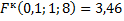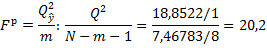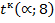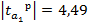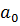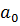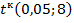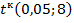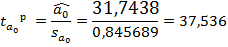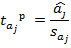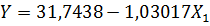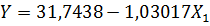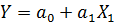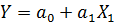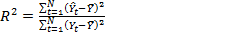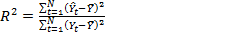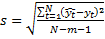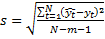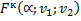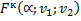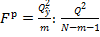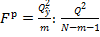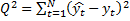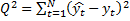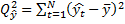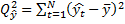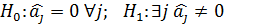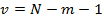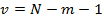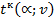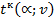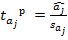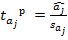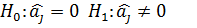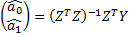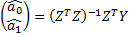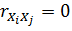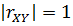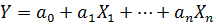    НазваниеКонтрольная работа 1 Построение факторной регрессионной модели
    Дата09.08.2018
    Размер119.22 Kb.
    Формат файлаdocx
    Имя файлаKontrolnaya_rabota__9571_1.docx
    ТипКонтрольная работа
    #49053


    Контрольная работа №1 «Построение факторной регрессионной модели.

    Исходные данные: файл исходные данные для контрольной работы. Вариант из Таблицы 1 берется строка по списку студента в группе. Из таблицы 2 выбираются столбцы данных Y и Х.

    Число наблюдений выборки: 50

    ТЕОРИЯ:

    1. Методика построения факторной регрессионной модели


    Спецификация
    Модель линейной регрессии в общем виде:

      1. Идентификация параметров модели линейной регрессии (метод МНК)


    Верификация
    Идентификация




      1. Проверка параметров модели на значимость.

    t-статистика Стъюдента:

    Табличное значения t-критерия:

      1. Дисперсионный анализ. Проверка существенности модели.



    • Вариация, обусловленная регрессией определяется как:

    • Остаточная вариация определяется как:

    Значение F-критерия Фишера составит:

    Табличное значения F-критерия:


    Проверка качества модели




      1. MSE,

    Коэффициент детерминации:

    1. Методика проверки остаточной компоненты на соответствие условиям Гаусса-Маркова

    2.1Проверка на случайность: критерий серий, основанный на медиане выборки.

    Упорядочивание уровней ряда (t ) в порядке возрастания.

    Определение выборочной медианы x(n)med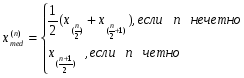



    Определение серии из плюсов и минусов: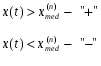



    Определение общего числа серий (последовательности плюсов и минусов) (t) и протяженность самой длинной серии (t).

    Выводы: ряд случаен, если выполняются следующие неравенства при 5 % уровне значимости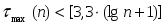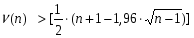





    2.2 Проверка на нормальный закон распределения

    Рассчитываем асимметрию (А) и ее среднеквадратическую ошибку А.

    Значение коэффициента асимметрии берем из распечатки Excel, надстройка «Анализ данных», Описательные статистики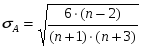



    Рассчитываем эксцесса (Э), и ее среднеквадратическую ошибку Э.

    Значение коэффициента эксцесса берем из распечатки Excel, надстройка «Анализ данных», Описательные статистики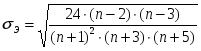



    Вывод: остаточная компонента имеет нормальное распределение, если выполняются следующие условия (для выборочной совокупности):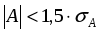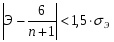

    ,

    Если выполняется хотя бы одно из неравенств: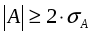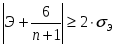

    ,

    то остаточная компонента не является даже приблизительно нормальными

    2.3 Проверка на независимость (Критерий Дарбина-Уотсона)

    Критерий Дарбина-Уотсона. .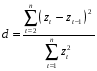

    Возможные значения критерия находятся в интервале [0 – 4].

    Если внутри ряда остатков зависимости не обнаружено, то значение критерия d колеблется вокруг 2.

    Эмпирическое значение d сравнивается с табличным значением.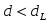

    - ряд содержит автокорреляцию (есть зависимость внутри ряда остатков.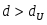

    - автокорреляция отсутствует.

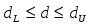    - необходимо дальнейшее исследование автокорреляции.
    ОПИСАНИЕ ЭТАПОВ КОНТРОЛЬНОЙ РАБОТЫ

    ЭТАП 1. Представление спецификаций факторной регрессионной модели.

      1. Логический анализ возможности и характера взаимосвязи объясняемой переменной Y и объясняющих переменных X с точки зрения экономической теории и практики и обоснование характера возможных взаимосвязей между результирующей переменной и переменными факторами.

      2. Исходное тестирование объясняющих переменных, проведение корреляционного анализа данных в Excel надстройка «Пакет анализа», корреляция.

    Результат: Выводы по результатам корреляционного анализа:

    • о степени взаимосвязи между зависимой переменной Y и независимыми переменными X (должна быть сильной)

    • о взаимосвязи между независимыми переменными (должна отсутствовать)

    Для определения силы связи можно воспользоваться шкалой Чеддока.

    ЭТАП 2. Идентификация параметров факторных регрессионных моделей.

    Цель: получение численных значений параметров однофакторной и многофакторной регрессии.

    2.1 Идентификация параметров однофакторной регрессионной модели в Excel. Пакет анализа, «Регрессия». В качестве независимой переменной выбирается наиболее значимая переменная из матрицы X (см. ЭТАП 1).

    2.2 Идентификация параметров многофакторной регрессионной модели в Excel. Пакет анализа, «Регрессия». В качестве независимых переменных рассматриваются все переменные матрицы X из индивидуального задания.

    В результате получаем два отчета в Excel. Записываем полученные уравнения однофакторной и многофакторной линейной регрессии.

    Например, однофакторная линейная регрессия

    общий вид регрессионной модели

    модель в явном виде

    ЭТАП 3. Проверка значимости параметров регрессионной модели

    На основании распечаток Excel делаем выводы с обоснованием о значимости параметров сначала приняв уровень значимости 10%, потом 5%. Если параметр многофакторной регрессии оказался незначимым, то исключаем его из модели и перестраиваем модель.

    Проверка осуществляется по двум моделям:

    • однофакторной линейной регрессии.

    • многофакторной линейной регрессии.

    Например, проверка константы на значимость.

    =2,31

    Вывод: параметр значим с вероятностью не менее 95%.

    Параметр значим с любой вероятностью.

    Вероятность
    80%
    90%
    95%
    98%
    99%




    1,4
    1,86
    2,31
    2,9
    3,36

    ЭТАП 3. Проверка значимости модели регрессии.

    На основании распечаток дисперсионного анализа отчета Excel пакет анализа, «Регрессия» делаем выводы с обоснованием о значимости модели приняв уровень значимости 10%, потом 5%.

    Проверка осуществляется по двум моделям:

    • однофакторной линейной регрессии.

    • многофакторной линейной регрессии.

    Например,

    Вывод: , модель существенна с вероятностью не менее 90%.

    ЭТАП 4. Оценка качества модели регрессии.

    Информационные характеристики качества однофакторной и многофакторной моделей из отчетов Excel, пакет анализа, «Регрессия» сводятся в Таблицу 1.

    Таблица 1.

    Сравнительные информационные характеристики регрессионных моделей

    Вид оцененных моделей регрессии
    Характеристики модели

    MSE (s)
    R2 (R2adj)
    F-статистика (Fкритич)

























    Например,

    Модель (в явном виде)
    Информационные характеристики качества однофакторной модели

    s
    F









    20,20
    71,6268

    В результате делается вывод, какая из двух моделей является лучшей (однофакторная линейная регрессия) или множественная регрессия.

    ЭТАП 5. Анализ остаточной компоненты. Выполнение требований Гаусса-Маркова.

    Остатки определяются по выбранной лучшей модели.

    Результаты сводятся в Таблицу 2.

    Таблица 2.

    Анализ остаточной компоненты

    Модель регрессии
    Характеристики остатков

    DWрасч (0-автокорреляция отсутствует/1- присутствует)
    Тест на случайность
    Mε (математическое ожидание случайной составляющей)
    Тест на нормальное распределение



















    написать администратору сайта