Контрольная работа по теории вероятности. Контрольная работа по математике. Контрольная работа 4 Задача 1

• Название: Контрольная работа 4 Задача 1
• Анкор: Контрольная работа по теории вероятности
• Дата: 13.10.2022
• Размер: 0.67 Mb.
• Имя файла: Контрольная работа по математике.docx
• Тип: Контрольная работа; #732286
• страница: 3 из 6

Задача 17. Результаты независимых измерений некоторой физической величины представлены в таблице. Построить график эмпирической функции распределения.

17.08

	12	17	22	27	32	37	42
	1	2	5	6	4	1	1

Решение:

Составим таблицу относительных частот:

	12	17	22	27	32	37	42
	1	2	5	6	4	1	1
	0,05	0,1	0,25	0,3	0 ,2	0,05	0,05

Тогда функция распределения имеет вид: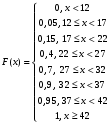


Построим график полученной функции: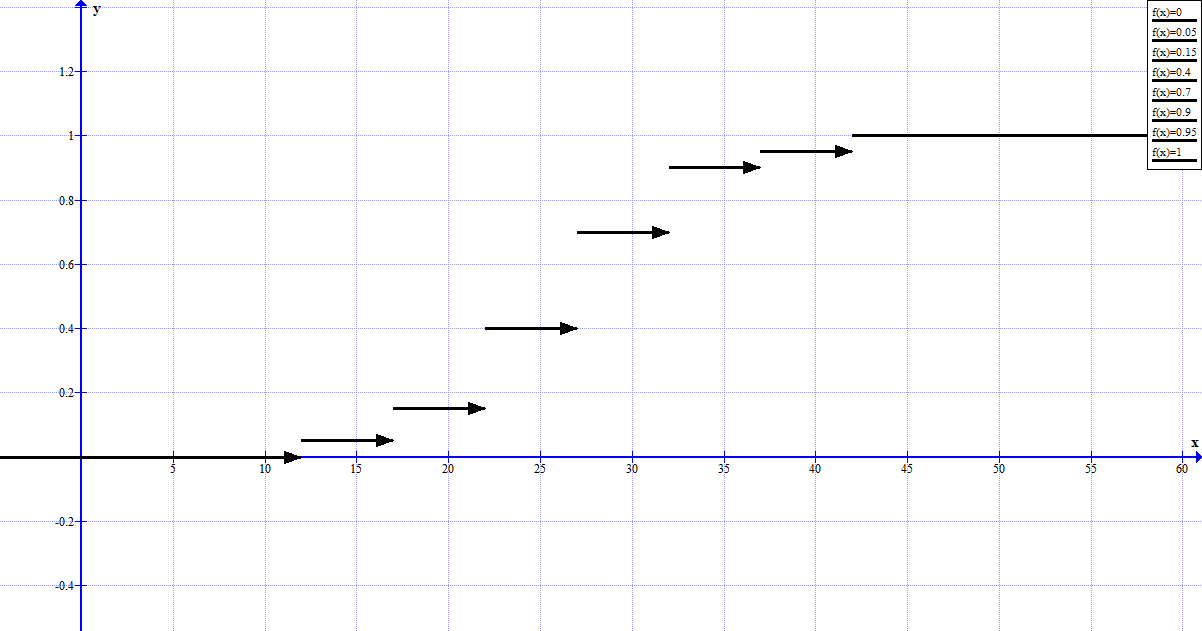


Задача 18.

18.08. Результаты измерений, полученных при испытаниях: 14; 16; 18. Найти исправленную выборочную дисперсию s².

Решение:

Найдем выборочное среднее:



Найдем выборочную дисперсию: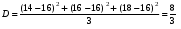



Тогда исправленная дисперсия равна



Ответ:
Задача 19. Результаты независимых измерений некоторой физической величины представлены в таблице. Вычислить выборочное среднее, выборочное среднеквадратическое отклонение, коэффициенты асимметрии и эксцесса.

19.08

Интервал	[12; 22]	(22; 32]	(32; 42]	(42; 52]	(52; 62]	(62; 72]	(72; 82]	(82; 92]
	2	7	16	22	31	13	7	2

Решение:

Вычислим выборочное среднее: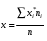

Составим рассчетную таблицу:

Интервал	[12; 22]	(22; 32]	(32; 42]	(42; 52]	(52; 62]	(62; 72]	(72; 82]	(82; 92]
, середина интервала	17	27	37	47	57	67	77	87
	2	7	16	22	31	13	7	2	Сумма
	34	189	592	1034	1767	871	539	174	5200

Тогда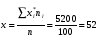



Найдем выборочную дисперсию: .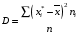

Составим рассчетную таблицу:

Интервал	[12; 22]	(22; 32]	(32; 42]	(42; 52]	(52; 62]	(62; 72]	(72; 82]	(82; 92]
, середина интервала	17	27	37	47	57	67	77	87
	1225	625	225	25	25	225	625	1225
	2	7	16	22	31	13	7	2	Сумма
	2450	4375	3600	550	775	2925	4375	2450	21500

Тогда



Откуда выборочное среднеквадратическое отклонение равно



Найдем центральный момент третьего порядка: 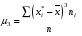. Составим рассчетную таблицу:

Интервал	[12; 22]	(22; 32]	(32; 42]	(42; 52]	(52; 62]	(62; 72]	(72; 82]	(82; 92]
, середина интервала	17	27	37	47	57	67	77	87
	-42875	-15625	-3375	-125	125	3375	15625	42875
	2	7	16	22	31	13	7	2	Сумма
	-85750	-109375	-54000	-2750	3875	43875	109375	85750	-9000

Тогда



Откуда коэффициент ассиметрии равен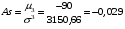



Найдем центральный момент 4 порядка: 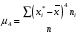. Составим рассчетную таблицу:

Интервал	[12; 22]	(22; 32]	(32; 42]	(42; 52]	(52; 62]	(62; 72]	(72; 82]	(82; 92]
, середина интервала	17	27	37	47	57	67	77	87
	1500625	390625	50625	625	625	50625	390625	1500625
	2	7	16	22	31	13	7	2	Сумма
	3001250	2734375	810000	13750	19375	658125	2734375	3001250	12972500

Тогда



Откуда коэффициент эксцесса равен