Контрольная работа по теории вероятности. Контрольная работа по математике. Контрольная работа 4 Задача 1
 Скачать 0.67 Mb.
|
|
Контрольная работа № 4 Задача 1. 1.08. В колоде 52 карты. Наудачу вытягивают одну карту. Какова вероятность того, что эта карта: а) дама; б) не туз; в) не черной масти? Решение: а) Общее число исходов  . В колоде 4 дамы, поэтому число благоприятных исходов равно  . Тогда искомая вероятность равна  . Ответ:  .б) Аналогично вероятность вытянуть туз равна  . Тогда искомая вероятность, как вероятность противоположного события, равна  .Ответ:  .в) Если карта будет не черной масти, то она будет красной масти, карт красной масти в колоде ровно половина, поэтому  . Тогда искомая вероятность равна  .Ответ:  Задача 2. Найти надежность системы, состоящей из 5 независимых элементов с надежностями: 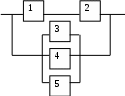 . 2.08. Решение: Найдем вероятность  того, ч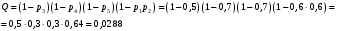то цепь выйдет из строя. Для этого нужно, чтобы одновременно из строя вышли элементы 3, 4, 5 и хотя бы один из элементов 1, 2.Тогда  Тогда надежность цепи равна  Ответ:  Задача 3. В урне m белых шаров и n черных. Случайным образом вынимают 2 шара. Какова вероятность того, что шары: а) оба белые; б) оба черные; в) один белый, а второй – черный?
Решение: а) Всего имеем 11 шаров в урне. 2 шара из 11 можно выбрать  способами – общее число исходов. Число благоприятных исходов равно  .Тогда искомая вероятность равна 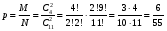 Ответ:  б) Аналогично 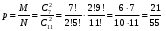. Число благоприятных исходов равно  . Тогда Ответ:  в) Аналогично . Число 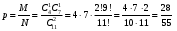благоприятных исходов равно  .Тогда  Ответ:  Задача 4. Студент идет сдавать экзамен, зная m вопросов из n. Чему равна вероятность у студента сдать экзамен, если для этого достаточно: а) ответить на k вопросов из s; б) ответить на все s вопросов; в) ответить не менее чем на один вопрос?
Решение: а) 6 вопросов из 50 можно выбрать  способами – общее число исходов. Число благоприятных исходов равно  (4 вопроса из тех, которые знает студент и 2 из 25 оставшихся). Тогда искомая вероятность равна 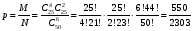 Ответ:  б) Аналогично, общее число исходов равно . Число благоприятных исходов равно  .Тогда 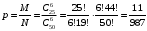 Ответ:  в) Найдем вероятность  проти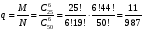воположного события – студент не ответит ни на один вопрос. Тогда , (все вопросы выбираются из тех, которые студент не знает).Тогда  Тогда искомая вероятность, как вероятность противоположного события, равна  Ответ:  Задача 5. Производительность первого конвейера в k раз больше, чем второго. Первый конвейер допускает p% брака, второй q% , брака. Детали с обоих конвейеров поступают на склад. а) Какова вероятность того, что случайно взятая со склада деталь будет стандартна? б) Какова вероятность того, что случайно взятая со склада деталь будет не стандартна? в) Случайно выбранная на складе деталь оказалась стандартной. Какова вероятность того, что деталь изготовлена на первом конвейере, на втором конвейере?
Решение: а) Пусть событие А заключается в том, что случайно взятая деталь стандартная. Обозначим события:  - деталь была выпущена на первом конвейере; - на втором.Тогда, по условию, 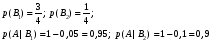 Тогда, по формуле полной вероятности,  Ответ:  б) поскольку событие, заключающееся в том, что случайно взятая со склада деталь будет не стандартна противоположно к событию А, то искомая вероятность равна  Ответ:  в) По формуле Байеса получим: 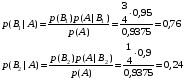 Ответ:  Задача 6. В первом ящике находится N деталей, из которых M – стандартны. Во втором ящике находится n деталей, из которых m стандартны. Без проверки на стандартность перекладывается из первого ящика во второй k деталей. Какова вероятность того, что случайно взятая из второго ящика деталь будет: а) стандартна; б) не стандартна?
Решение: а) Пусть событие А заключается в том, что деталь стандартна. Обозначим события:  – из пер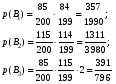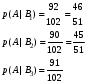вого ящика во второй переложили две стандартные детали; – 2 нестардантные детали; – одну стандартную и одну нестандартную деталь.Тогда   Тогда, по формуле полной вероятности,  Ответ:  б) Поскольку искомая вероятность – вероятность события, противоположного к событию, вероятность которого найдена в пункте а), то  Ответ:  Задача 7. На клумбу посеяно n семян цветов одного сорта со всхожестью P. Полагая, что  – количество взошедших семян, найти вероятности событий: =m; m; m1 m2; m1< 1; а)
Решение: По условию,  Используя формулу Бернулли, найдем:  Аналогично найдем вероятности 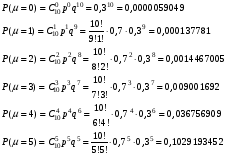 Тогда 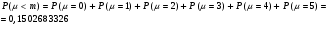 Найдем вероятности 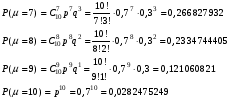 Тогда 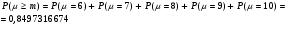 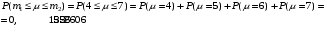  Найдем   б)
Решение: Используя локальную теорему Лапласа, найдем: 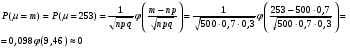 Используя интегральную теорему Лапласа, найдем: 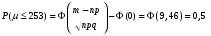 Тогда 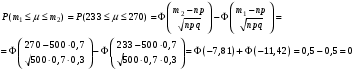 Найдем  Найдем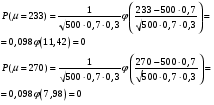 Тогда  Найдем 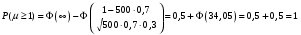 Найдем 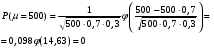 Тогда  |