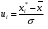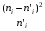Контрольная работа по теории вероятности. Контрольная работа по математике. Контрольная работа 4 Задача 1

• Название: Контрольная работа 4 Задача 1
• Анкор: Контрольная работа по теории вероятности
• Дата: 13.10.2022
• Размер: 0.67 Mb.
• Имя файла: Контрольная работа по математике.docx
• Тип: Контрольная работа; #732286
• страница: 6 из 6

9. 
   
   

2) Разбив выборку на 5 интервалов и посчитав количество вариант, попадающих в каждый интервал, получим сгрупированный статистический ряд:

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
	9	27	36	21	7

3) Построим гистограмму выборки: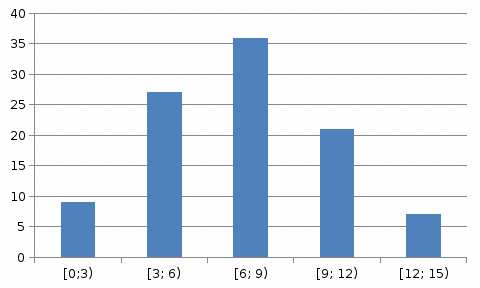



4) Составим таблицу относительных частот:

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
	9	27	36	21	7
	0,09	0,27	0,36	0,21	0,07

Тогда функция распределения имеет вид: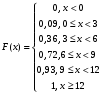



Тогда график функции распределения имеет вид: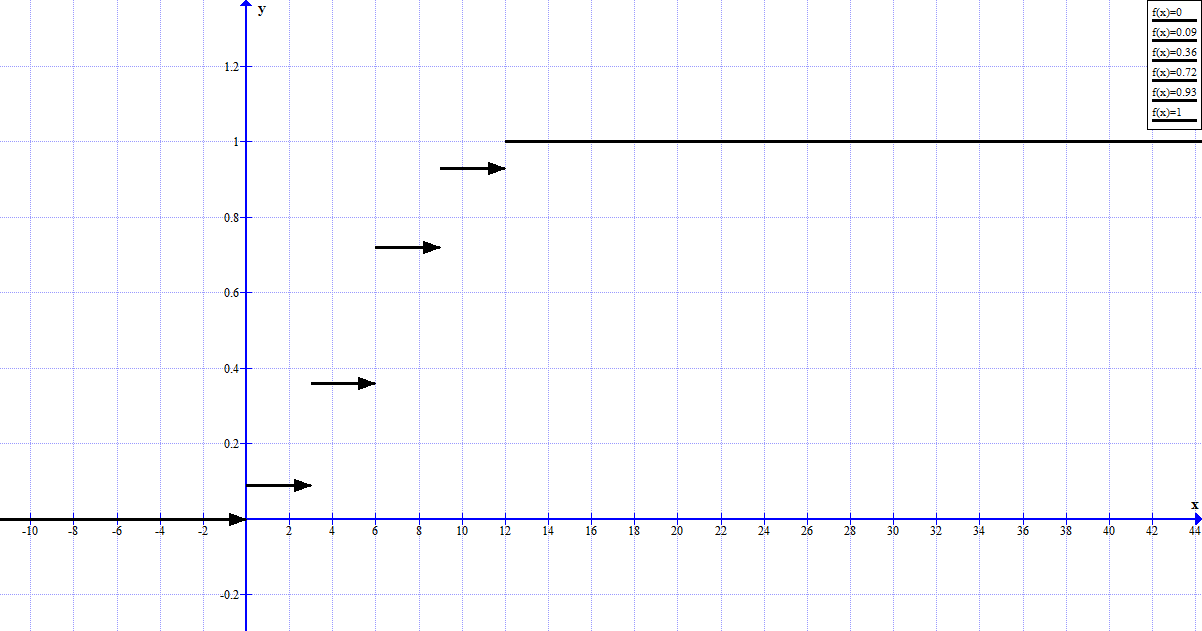



5) Найдем выборочное среднее. Составим рассчетную таблицу

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
, середина интервала	1,5	4,5	7,5	10,5	13,5
	9	27	36	21	7	Сумма
	13,5	121,5	270	220,5	94,5	720

10. 
    
    

Тогда .

Найдем выборочную дисперсию. Составим рассчетную таблицу

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
, середина интервала	1,5	4,5	7,5	10,5	13,5
	9	27	36	21	7
	32,49	7,29	0,09	10,89	39,69	Сумма
	292,41	196,83	3,24	228,69	277,83	999

Тогда выборочная дисперсия равна

– выборочное среднеквадратичное отклонение.

Найдем центральные моменты третьего и четвертого порядка. Составим рассчетную таблицу:

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
, середина интервала	1,5	4,5	7,5	10,5	13,5
	9	27	36	21	7
	-185,193	-19,683	0,027	35,937	250,047	Сумма
	-1666,74	-531,441	0,972	754,677	1750,329	307,8
	1055,6	53,1441	0,0081	118,5921	1575,296
	9500,401	1434,891	0,2916	2490,434	11027,07	24453,09

Тогда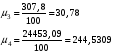



Откуда коэффициент ассиметрии равен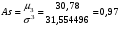



Коэффициент эксцесса: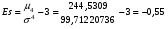



6) Найдем исправленную дисперсию:



Найдем доверительный интервал для математического ожидания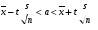



При , получ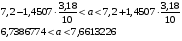им

Тогда



7) Вычислим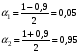





Находим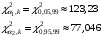



Тогда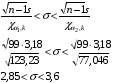


8) Найдем теоретические частоты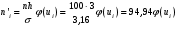



Составим рассчетную таблицу:

Интервал	[0;3)	[3; 6)	[6; 9)	[9; 12)	[12; 15)
, середина интервала	1,5	4,5	7,5	10,5	13,5
	9	27	36	21	7
	-1,8038	-0,85443	0,094937	1,044304	1,993671
	0,078412	0,276937	0,397148	0,231257	0,054678
	7,444414	26,29243	37,70528	21,95558	5,191096

Составим рассчетную таблицу, из которой найдем наблюдаемое значение критерия Стьюдента :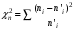

	9	27	36	21	7
	7,444414	26,29243	37,70528	21,95558	5,191096
	2,419848	0,500655	2,90798	0,913133	3,272134	Сумма
	0,325056	0,019042	0,077124	0,04159	0,630336	1,093147

При числу степеней свободы при уровнях значимости .