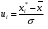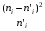Задача 20. Результаты независимых измерений некоторой физической величины представлены в таблице. Найти доверительный интервал для математического ожидания при доверительной вероятности 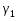 ; доверительный интервал для среднеквадратического отклонения при доверительной вероятности ; доверительный интервал для среднеквадратического отклонения при доверительной вероятности 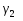 . .
20.08
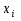
|
5
|
8
|
11
|
14
|
17
|
20
|
23
|
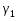
|
= 0,9
|
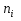
|
1
|
1
|
5
|
6
|
4
|
2
|
1
|
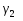
|
= 0,8
|
Решение:
Найдем выборочную среднюю. Составим рассчетную таблицу
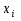
|
5
|
8
|
11
|
14
|
17
|
20
|
23
|
|
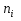
|
1
|
1
|
5
|
6
|
4
|
2
|
1
|
Сумма
|
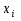 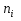
|
5
|
8
|
55
|
84
|
68
|
40
|
23
|
283
|
Тогда
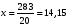
Найдем выборочную дисперсию. Составим рассчетную таблицу:
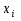
|
5
|
8
|
11
|
14
|
17
|
20
|
23
|
|
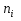
|
1
|
1
|
5
|
6
|
4
|
2
|
1
|
|
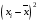
|
83,7225
|
37,8225
|
9,9225
|
0,0225
|
8,1225
|
34,2225
|
78,3225
|
Сумма
|
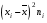
|
83,7225
|
37,8225
|
49,6125
|
0,135
|
32,49
|
68,445
|
78,3225
|
350,55
|
Тогда
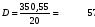
Откуда
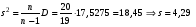
Найдем доверительный интервал для математического ожидания
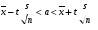
При 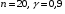 , получим , получим 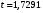
Тогда
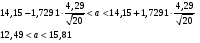
Найдем доверительный интервал для среднеквадратического отклонения
Вычислим
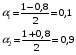
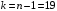
Находим
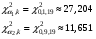
Тогда
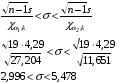
Задача 21. Результаты 100 измерений некоторой физической величины представлены в таблице сгруппированным вариационным рядом. Требуется с помощью критерия Пирсона проверить гипотезу 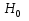 о том, что генеральная совокупность распределена по нормальному закону. о том, что генеральная совокупность распределена по нормальному закону.
21.08
Интервал
|
[37; 47]
|
(47; 57]
|
(57; 67]
|
(67; 77]
|
(77; 87]
|
(87; 97]
|
(97; 107]
|
(107; 117]
|
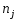
|
2
|
7
|
16
|
22
|
31
|
13
|
7
|
2
|
Решение:
Найдем выборочную среднюю. Составим рассчетную таблицу:
Интервал
|
[37; 47]
|
(47; 57]
|
(57; 67]
|
(67; 77]
|
(77; 87]
|
(87; 97]
|
(97; 107]
|
(107; 117]
|
|
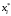 , середина интервала , середина интервала
|
42
|
52
|
62
|
72
|
82
|
92
|
102
|
112
|
|
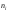
|
2
|
7
|
16
|
22
|
31
|
13
|
7
|
2
|
Сумма
|
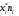
|
84
|
364
|
992
|
1584
|
2542
|
1196
|
714
|
224
|
7700
|
Тогда
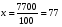
Найдем выборочную дисперсию. Составим рассчетную таблицу
Интервал
|
[37; 47]
|
(47; 57]
|
(57; 67]
|
(67; 77]
|
(77; 87]
|
(87; 97]
|
(97; 107]
|
(107; 117]
|
|
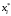 , середина интервала , середина интервала
|
42
|
52
|
62
|
72
|
82
|
92
|
102
|
112
|
|
|
2
|
7
|
16
|
22
|
31
|
13
|
7
|
2
|
|
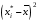
|
1225
|
625
|
225
|
25
|
25
|
225
|
625
|
1225
|
Сумма
|
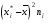
|
2450
|
4375
|
3600
|
550
|
775
|
2925
|
4375
|
2450
|
21500
|
Тогда
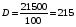
Откуда выборочное среднеквадратическое отклонение равно
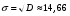
Найдем теоретические частоты
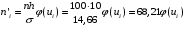
Составим рассчетную таблицу:
Интервал
|
[37; 47]
|
(47; 57]
|
(57; 67]
|
(67; 77]
|
(77; 87]
|
(87; 97]
|
(97; 107]
|
(107; 117]
|
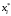 , середина интервала , середина интервала
|
42
|
52
|
62
|
72
|
82
|
92
|
102
|
112
|
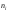
|
2
|
7
|
16
|
22
|
31
|
13
|
7
|
2
|
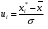
|
-2,38745
|
-1,70532
|
-1,02319
|
-0,34106
|
0,341064
|
1,023192
|
1,705321
|
2,387449
|
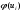
|
0,023078
|
0,093201
|
0,23636
|
0,376401
|
0,376401
|
0,23636
|
0,093201
|
0,023078
|
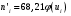
|
1,57412
|
6,357235
|
16,12211
|
25,67429
|
25,67429
|
16,12211
|
6,357235
|
1,57412
|
Составим рассчетную таблицу, из которой найдем наблюдаемое значение критерия Стьюдента 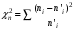 : :
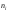
|
2
|
7
|
16
|
22
|
31
|
13
|
7
|
2
|
|
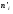
|
1,57412
|
6,357235
|
16,12211
|
25,67429
|
25,67429
|
16,12211
|
6,357235
|
1,57412
|
|
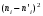
|
0,181374
|
0,413147
|
0,014911
|
13,50041
|
28,36319
|
9,747571
|
0,413147
|
0,181374
|
Сумма
|
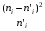
|
0,115222
|
0,064988
|
0,000925
|
0,525834
|
1,104731
|
0,604609
|
0,064988
|
0,115222
|
2,59652
|
Тогда
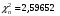
По числу степеней свободы 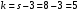 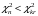 при уровне значимости при уровне значимости 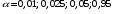 , поэтому при данных уровнях значимости гипотезу о нормальном распределении следует принять. , поэтому при данных уровнях значимости гипотезу о нормальном распределении следует принять.
|
 Скачать 0.67 Mb.
Скачать 0.67 Mb.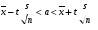
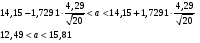
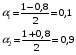
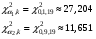
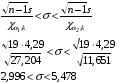
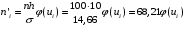
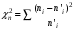 :
: