Контрольная работа по теории вероятности. Контрольная работа по математике. Контрольная работа 4 Задача 1

• Название: Контрольная работа 4 Задача 1
• Анкор: Контрольная работа по теории вероятности
• Дата: 13.10.2022
• Размер: 0.67 Mb.
• Имя файла: Контрольная работа по математике.docx
• Тип: Контрольная работа; #732286
• страница: 2 из 6

Задача 8. Дискретная случайная величина задана таблицей. Найти неизвестную вероятность , математическое ожидание M(X) и вероятность попадания случайной величины в интервал .

8.08.  = 1;  = 4,2
	–2	–1	0	4	7
		0,1	0,2	0,1	0,1

Решение:

найдем из условия . Тогда



Найдем математическое ожидание:



Найдем

.

Ответ: ; ; .
Задача 9. Дискретная случайная величина задана таблицей. Найти неизвестное значение x_i , неизвестную вероятность P_i , дисперсию DX, среднеквадратичное отклонение _x и вероятность событий Х < MХ и Х  MХ.


9.08. MX = 1

xi	x1	0,8	1,2	1,6	2,0
Pi	0,2	P2	0,2	0,1	0,1

Решение: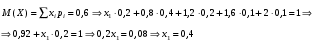

найдем из условия . Тогда





Найдем дисперсию: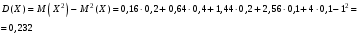

Найдем среднеквадратическое отклонение:



Найдем вероятность



Найдем вероятность



Задача 10. Дана функция распределения F(x) случайной величины X. Найти плотность распределения вероятности f(x), математическое ожидание M(X) и вероятность попадания случайной величины в интервал .
10.08.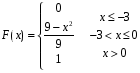



Решение:

Найдем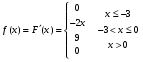



Найдем математическое ожидание: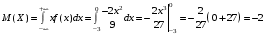



Найдем вероятность


Задача 11. Дана функция распределения F(x) случайной величины Х. Найти плотность распределения вероятности f(x), математическое ожидание MX, дисперсию DX, среднеквадратичное отклонение _x, построить графики функций F(x) и f(x), найти вероятность попадания случайной величины в интервал х₁  X  x₂.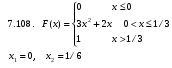



<sub>Решение:

Найдем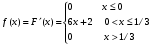</sub>



Найдем математическое ожидание: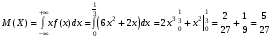



Найдем дисперсию: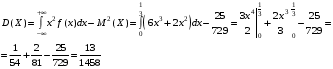



Найдем среднеквадратическое отклонение: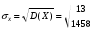



Найдем вероятность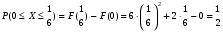



Построим график :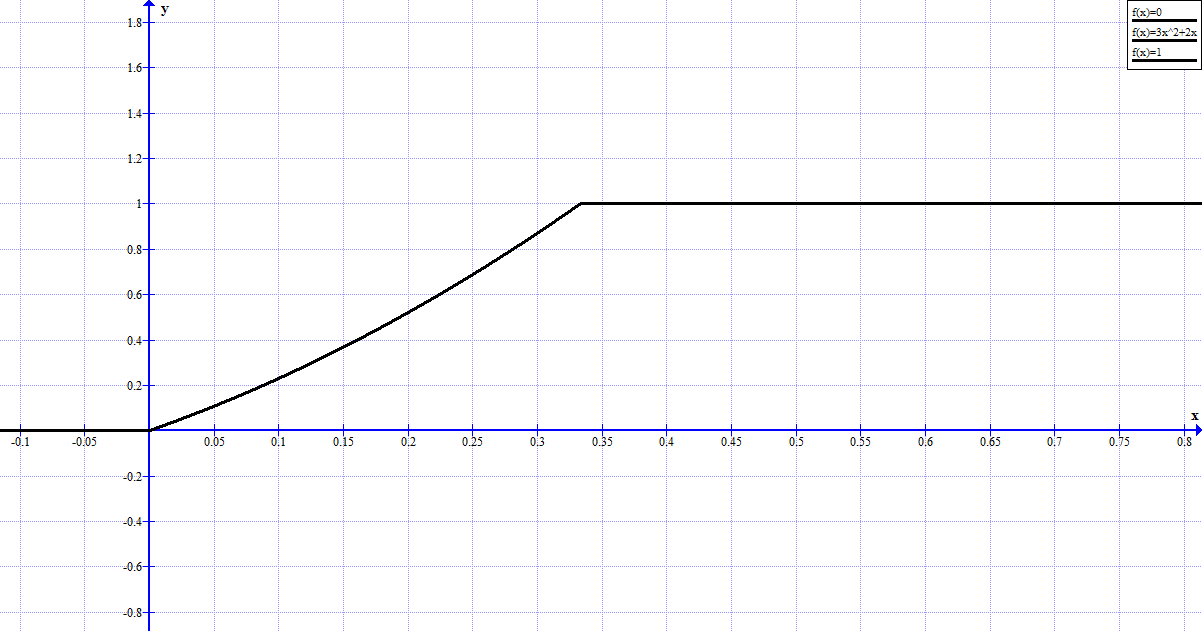



Построим график :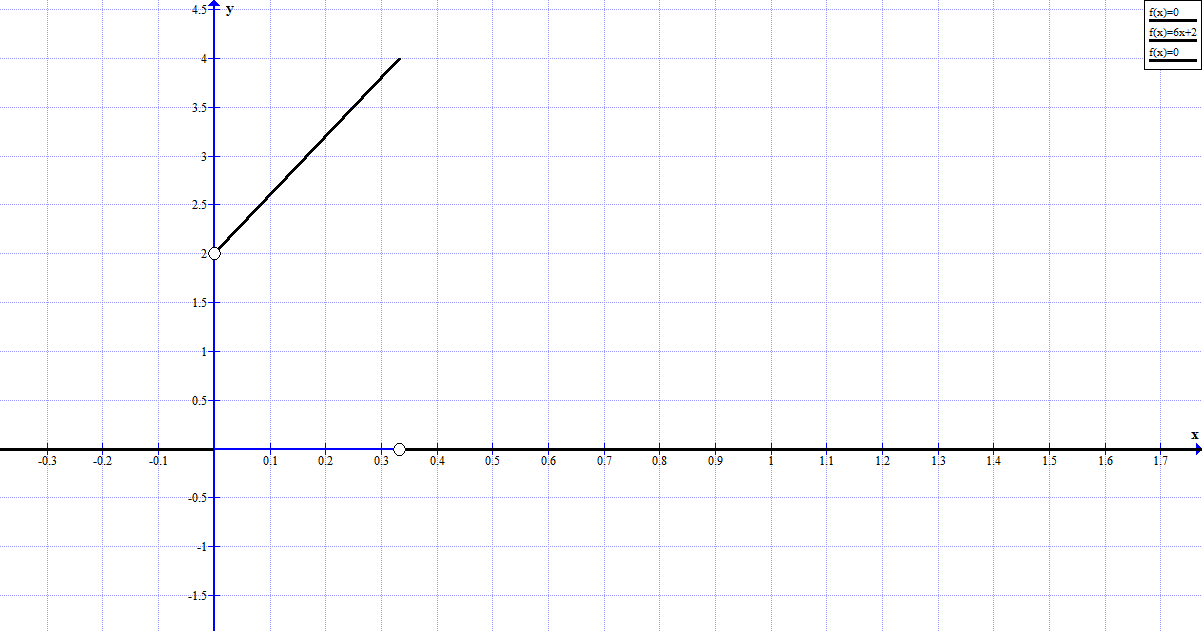


Задача 12. Дана функция плотности распределения f(x) случайной величины Х. Найти параметр A, функцию распределения F(x), построить графики функций F(x) и f(x), вычислить математическое ожидание МX, дисперсию DX, среднеквадратичное отклонение _x, вероятности событий X < x₀, X > x₀, x₁  X  x₂.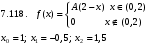


Решение:

Значение А найдем из условия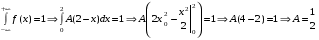



Найдем функцию распределения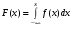

При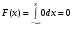



При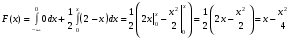



При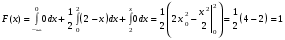



Тогда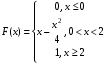



Найдем математическое ожидание: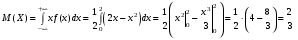



Найдем дисперсию: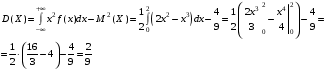



Найдем среднеквадратическое отклонение: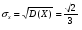


Найдем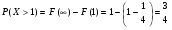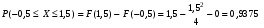







Построим график :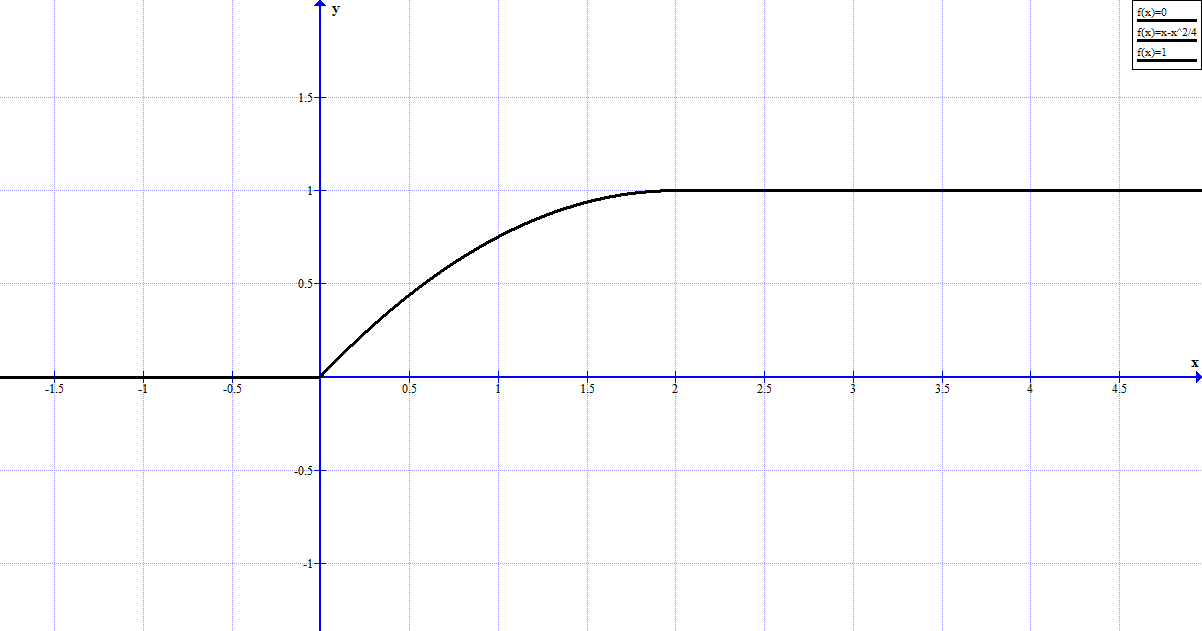



Построим график :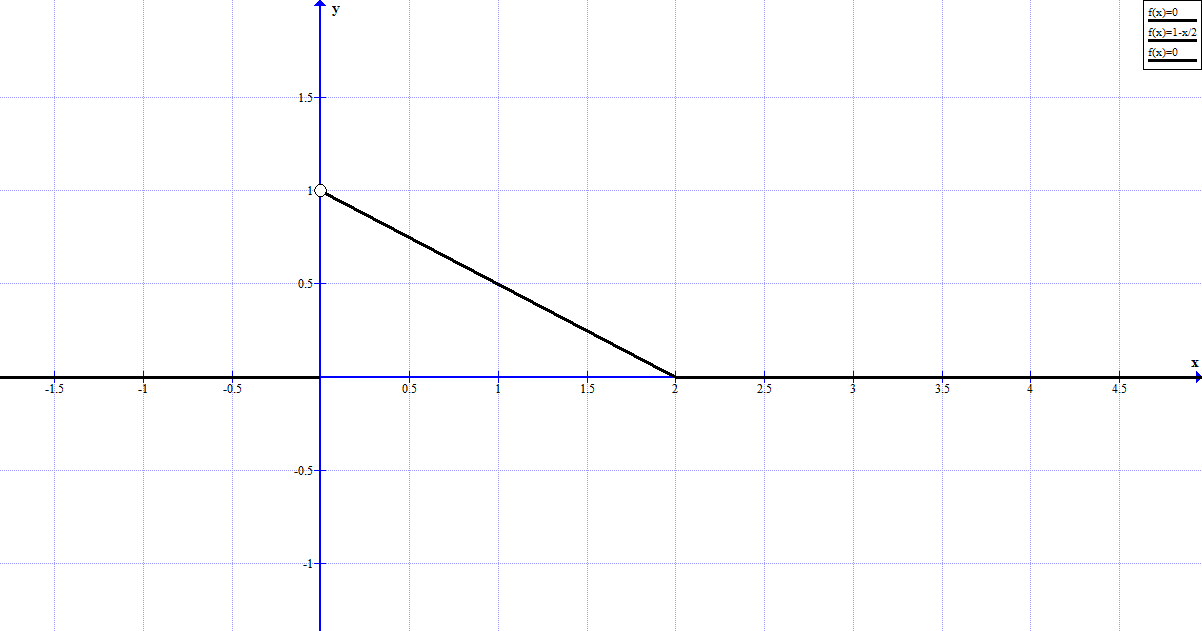


Задача 13. Дискретная случайная величина X может принимать только два значения х₁ и х₂, причем х₁ < х₂. Известны вероятность P₁ возможного значения х₁, математическое ожидание МХ и дисперсия DХ. Найти закон распределения случайной величины Х.

Задачи	13.08
P1	0,9
MX	1,8
DX	5,76

Решение:

Найдем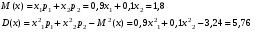



Получим систему: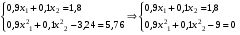



Из первого уравнения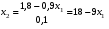



Подставим во второе уравнение: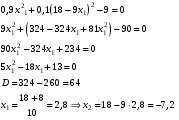



Или



Поскольку по условию х₁ < х₂, то , .

Получим закон распределения:

	1	9
	0,9	0,1

Задача 14. Непрерывная случайная величина распределена по нормальному закону с параметрами аи . Найти вероятности событий Х < А; X > B; А X  B;X – a < t. Найти интервал [а – , а + ], в который случайная величина попадает с вероятностью Р.

Задачи	14.08
а	6
	3
А	2
В	11
t	0,5
Р	0,9

Решение:

Найдем вероятность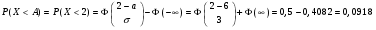

Найдем



Найдем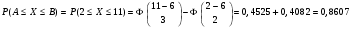



Найдем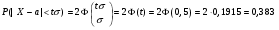



Найдем интервал [а – , а + ], в который случайная величина попадает с вероятностью 0,9: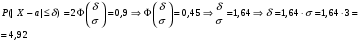

Тогда интервал имеет вид:

[6– 4,92, 6 + 4,92] или [1,08, 10,92].

Задача 15. Результаты независимых измерений некоторой физической величины представлены в таблице. Построить полигон относительных частот.

	17	20	23	26	29	32	35
	1	2	5	6	4	1	1

Решение:

Составим таблицу относительных частот .

Получим:

	17	20	23	26	29	32	35
	1	2	5	6	4	1	1
	0,05	0,1	0,25	0,3	0,2	0,05	0,05

Получим полигон относительных частот: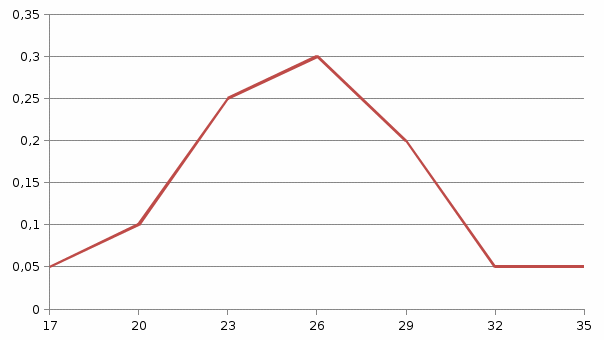


Задача 16. В таблице приведена первичная выборка объема n= 100. Составить вариационный ряд и сгруппированный статистический ряд. Построить гистограмму выборки.
16.08

18,70	21,70	16,55	11,71	18,62	18,34	18,08	9,93	21,36	18,27
14,29	18,79	16,62	19,28	7,95	21,13	20,73	13,82	16,52	12,65
20,51	11,30	20,84	13,80	20,70	21,18	14,54	12,04	20,47	20,73
19,83	20,15	8,88	11,92	14,82	17,08	17,62	12,49	18,13	21,36
18,72	16,02	12,97	18,12	16,00	18,52	8,18	17,11	25,01	12,82
16,14	19,66	19,30	16,08	16,65	12,82	13,99	15,54	10,58	12,84
15,05	21,06	24,22	15,74	19,15	13,62	22,29	10,22	22,93	13,26
11,68	14,44	19,99	11,52	17,71	15,60	10,97	23,25	20,83	20,62
9,74	16,68	17,94	8,97	15,54	19,67	20,50	19,27	23,53	19,71
9,32	23,55	26,21	19,57	25,54	20,62	18,59	26,29	16,35	25,59

Решение:

Проранжировав данные и подсчитав частоты, получим вариационный ряд:

7,95	1
8,18	1
8,88	1
8,97	1
9,32	1
9,74	1
9,93	1
10,22	1
10,58	1
10,97	1
11,3	1
11,52	1
11,68	1
11,71	1
11,92	1
12,04	1
12,49	1
12,65	1
12,82	2
12,84	1
12,97	1
13,26	1
13,62	1
13,8	1
13,82	1
13,99	1
14,29	1
14,44	1
14,54	1
14,82	1
15,05	1
15,54	2
15,6	1
15,74	1
16	1
16,02	1
16,08	1
16,14	1
16,35	1
16,52	1
16,55	1
16,62	1
16,65	1
16,68	1
17,08	1
17,11	1
17,62	1
17,71	1
17,94	1
18,08	1
18,12	1
18,13	1
18,27	1
18,34	1
18,52	1
18,59	1
18,62	1
18,7	1
18,72	1
18,79	1
19,15	1
19,27	1
19,28	1
19,3	1
19,57	1
19,66	1
19,67	1
19,71	1
19,83	1
19,99	1
20,15	1
20,47	2
20,5	1
20,51	1
20,62	2
20,7	1
20,73	2
20,83	1
20,84	1
21,06	1
21,13	1
21,18	1
21,36	2
21,7	1
22,29	1
22,93	1
23,25	1
23,53	1
23,55	1
24,22	1
25,01	1
25,54	1
25,59	1
26,21	1

Разобьем выборку на 5 интервалов. Посчитав количество вариант, попадающих в каждый интервал, получим интервальный ряд:

Интервал	[7; 11)	[11; 15)	[15; 19)	[19; 23)	[23; 27)
	10	21	31	29	9

Построим гистограмму выборки: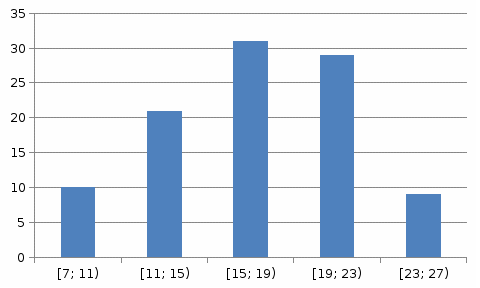