лабораторнаю. Контрольная работа 9 Обыкновенные дифференциальные уравнения тема обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка
 Скачать 0.86 Mb.
|
|
Ответ.  ;  .Задание 6. Решить уравнение  .Решение. Правая часть уравнения представляет собой дифференциальное уравнение с постоянными коэффициентами. Выпишем общее решение однородного дифференциального уравнения второго порядка 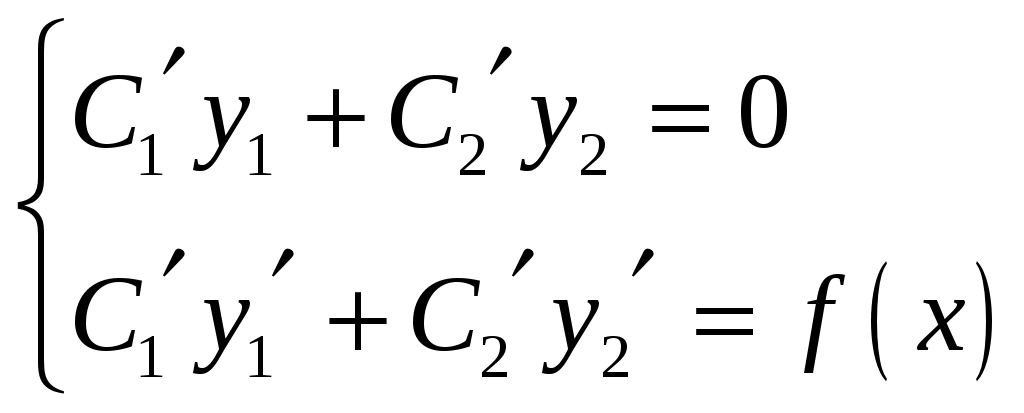 . Так как корнями соответствующего характеристического уравнения  являются числа  , то общее решение данного уравнения, как известно, имеет вид  . Правая часть исходного уравнения  не позволяет найти частное решение  неоднородного уравнения методом подбора (или неопределенных коэффициентов) поэтому воспользуемся для его нахождения методом вариации произвольных постоянных. Поэтому будем искать частное решение в виде:  , предполагая, что здесь  и  (мы воспользовались видом найденной фундаментальной системы решений однородного уравнения), а  и  решения следующей системы дифференциальных уравнений: таким образом 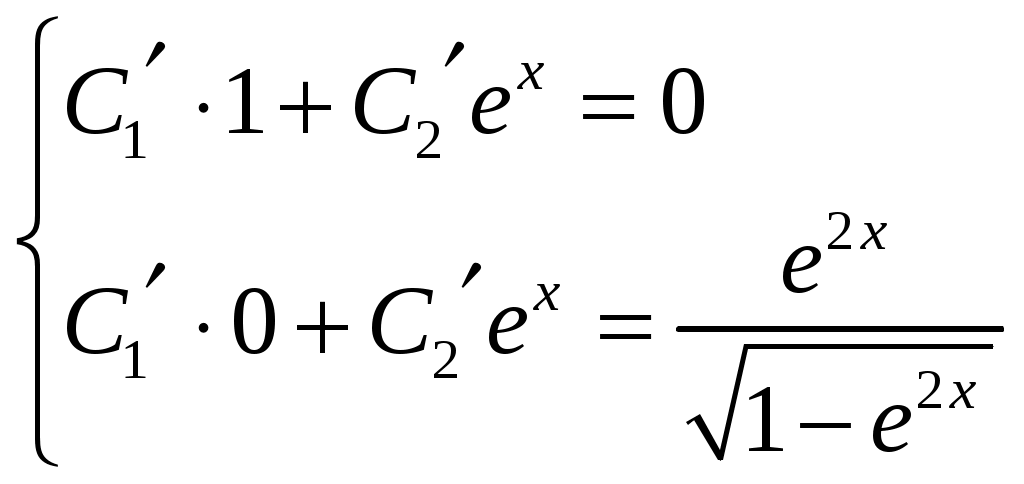 .Из второго уравнения выпишем  . Проинтегрировав, получим  (постоянную интегрирования будем полагать равной нулю). Теперь, подставляя значение  в первое уравнение системы, получим дифференциальное уравнение для функции  :  . Вновь интегрируя, запишем:  .Таким образом, частное решение исходного уравнения имеет вид  , выпишем общее решение неоднородного дифференциального уравнения  Ответ.  .Контрольная работа №9. Вариант 1. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 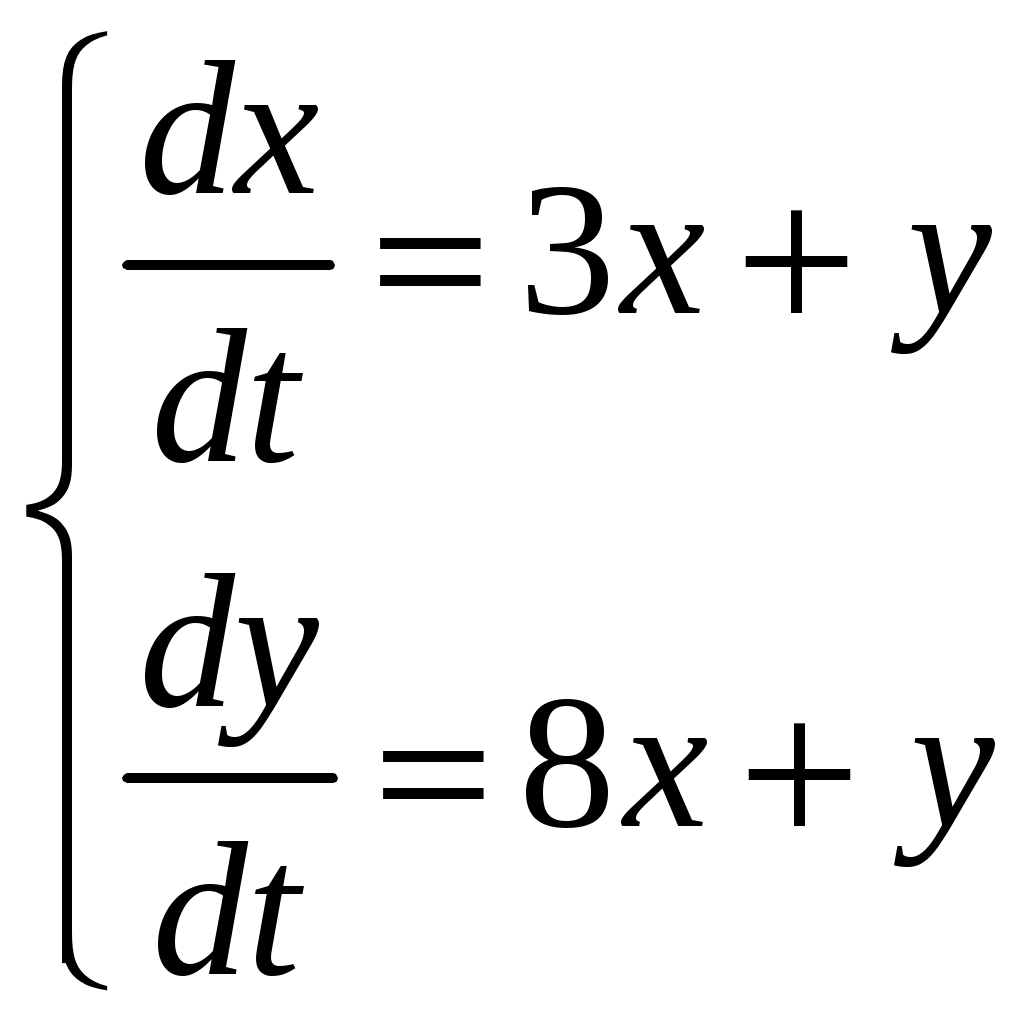 .Записать уравнение кривой, проходящей через точку  , если известно, что угловой коэффициент касательной в любой ее точке в 3 раз больше углового коэффициента прямой, соединяющей точку А с началом координат.Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 2. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 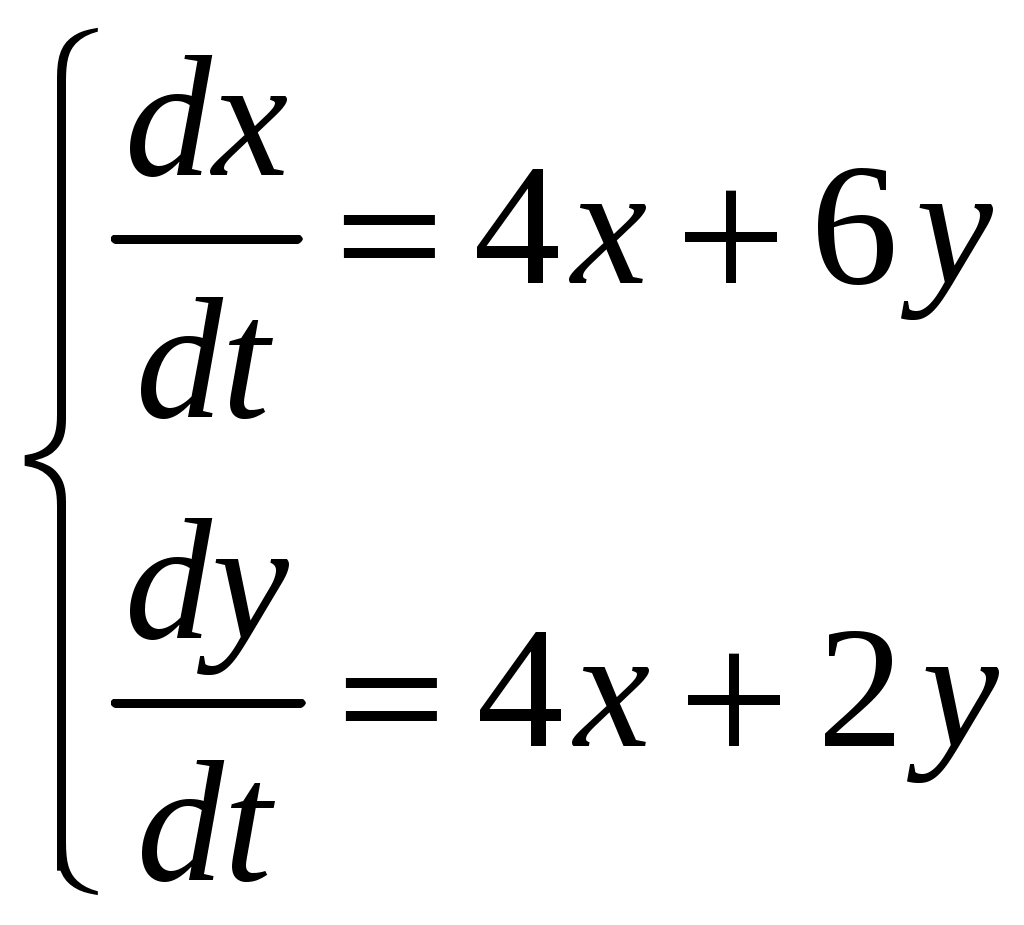 .Найти уравнение кривой, проходящей через точку A(10, 10) и, обладающей тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания. Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 3. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 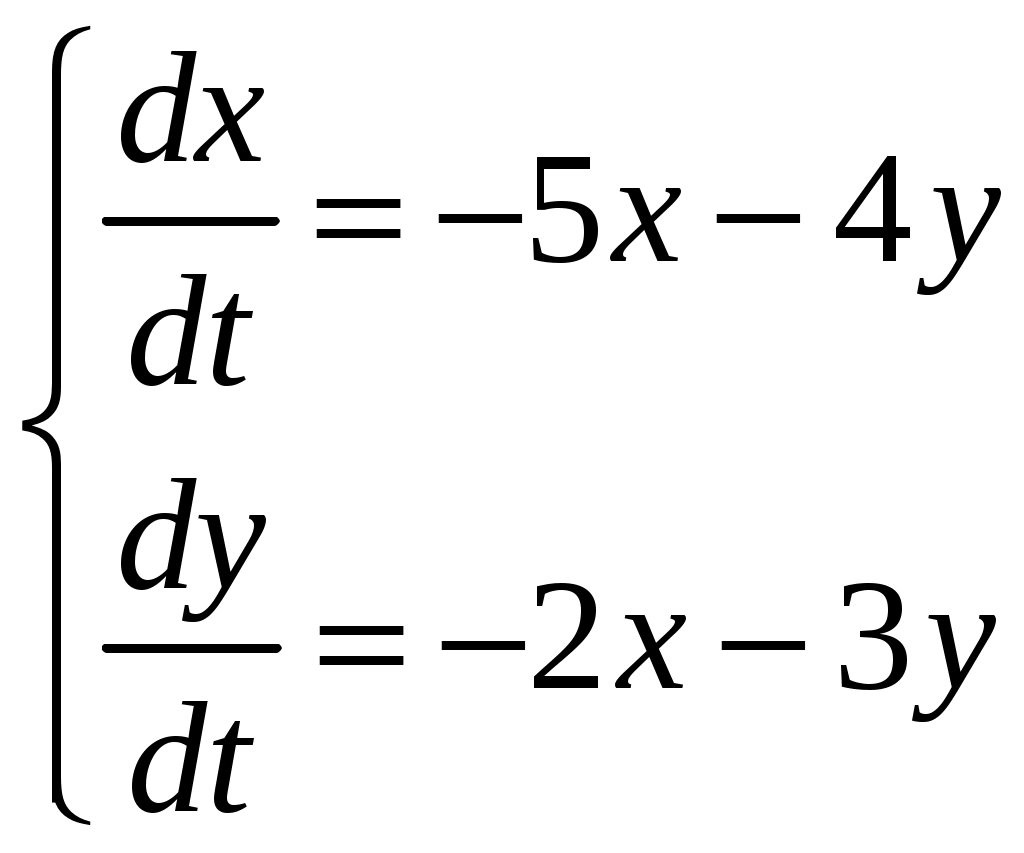 . Найти уравнение кривой, проходящей через точку A(1, 4) и, обладающей тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен удвоенной абсциссе точки касания. Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 4. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 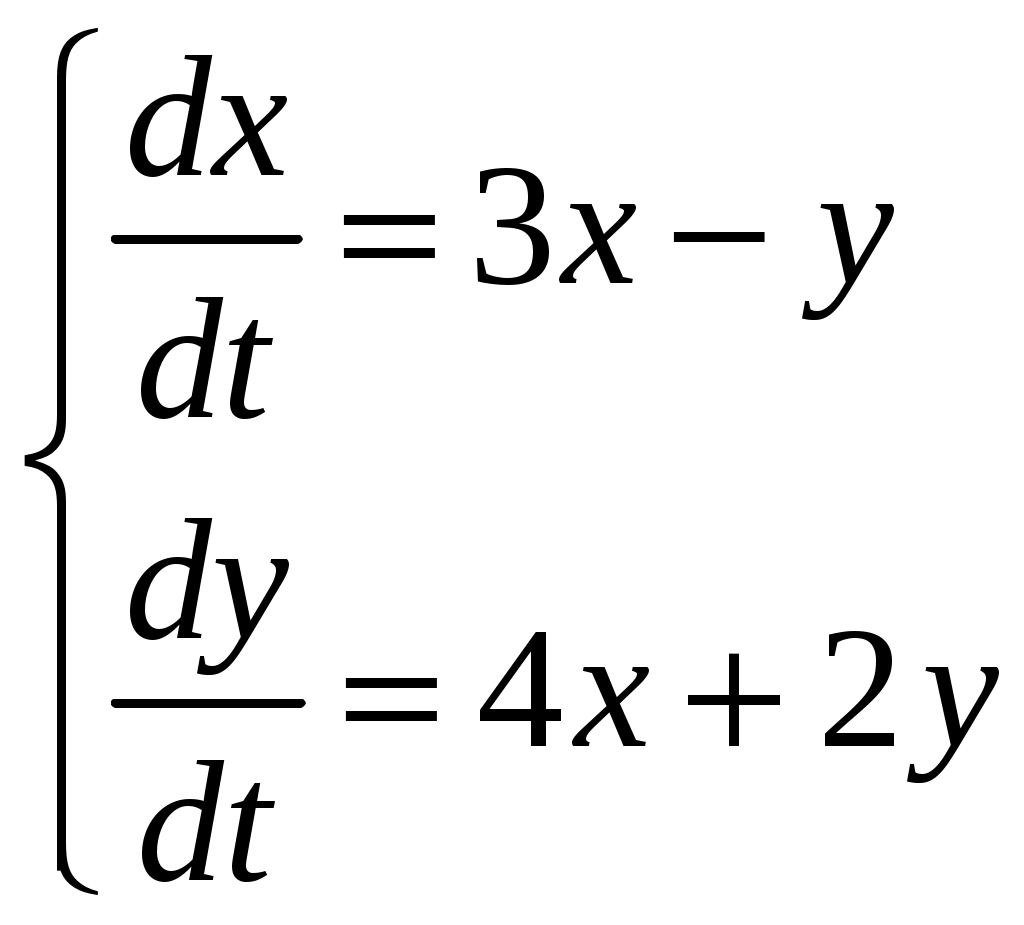 . Найти уравнение кривой, проходящей через точку B(3, 4) и, обладающей тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен удвоенному модулю радиус-вектора точки касания. Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 5. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 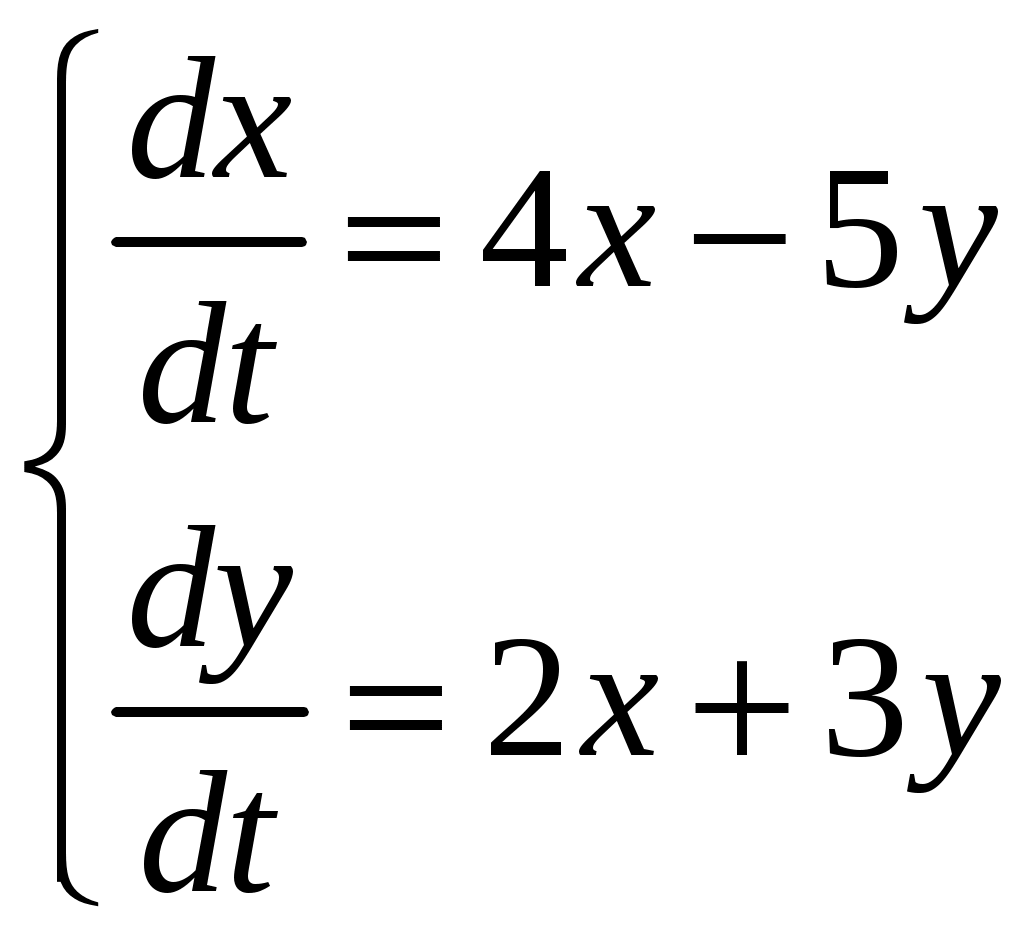 . В силу закона Ньютона скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Если температура воздуха равна  и тело в течение часа охлаждается от  до  , то через сколько минут (с момента начала охлаждения) его температура понизится до  ?Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 6. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 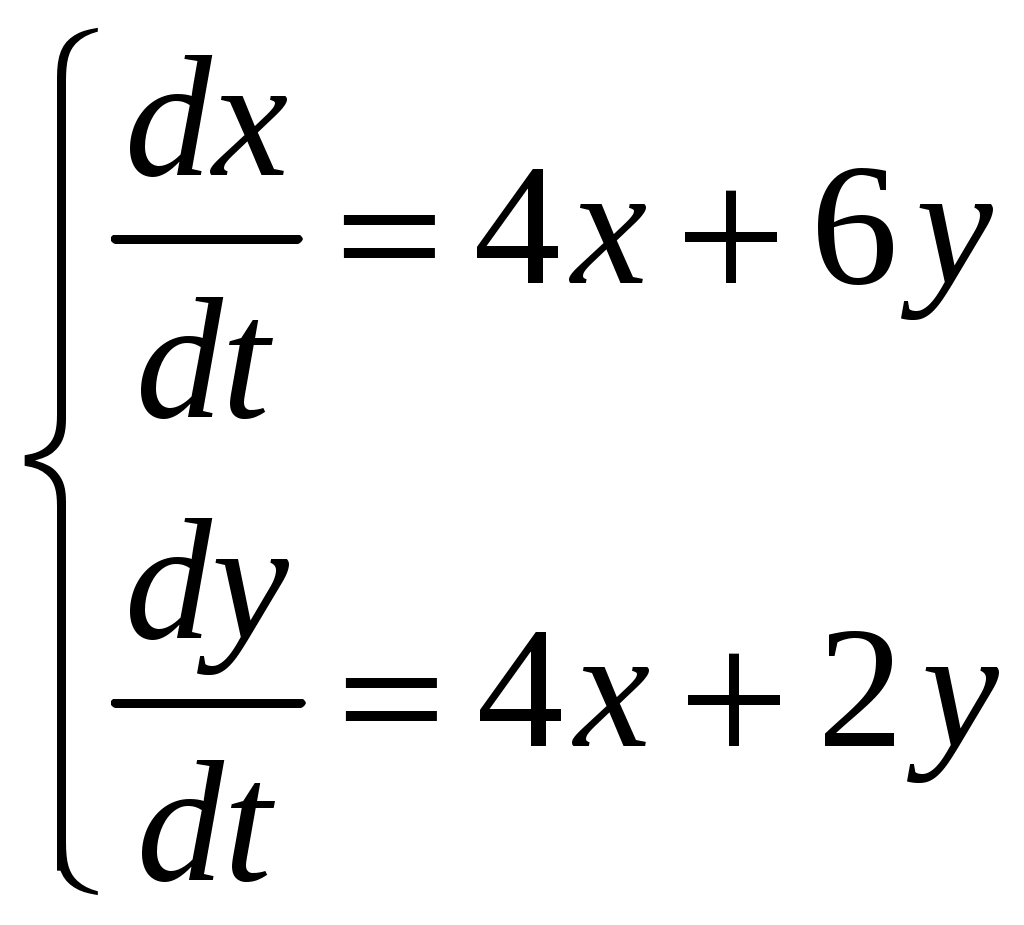. Определить путь, Тело массой  движется прямолинейно. На него действует сила, пропорциональная времени, протекшему от момента, когда  (коэффициент пропорциональности 2). Кроме того, тело испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности 3). Найти скорость в момент  сек.Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  .Контрольная работа №9. Вариант 7. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  Найти общее решение системы дифференциальных уравнений 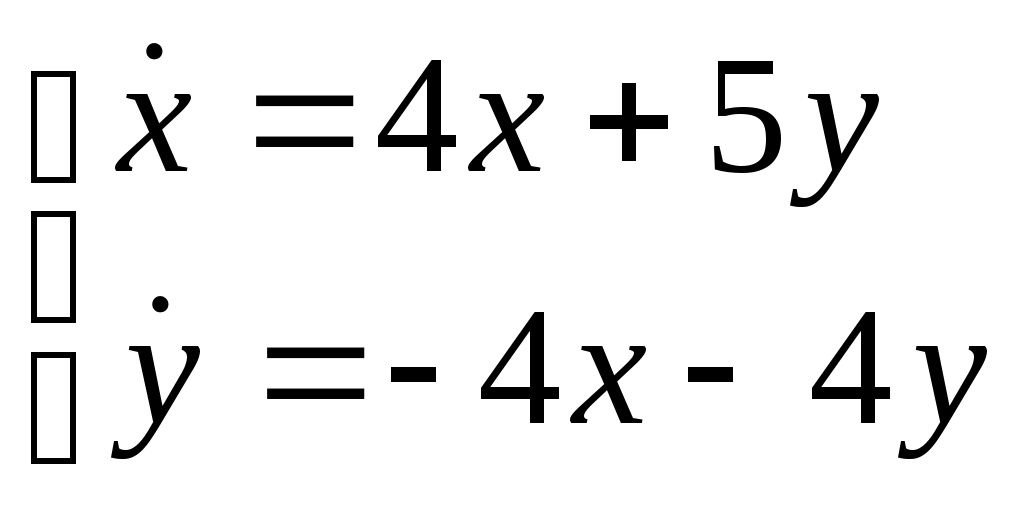 . Найти уравнение кривой, проходящей через т. A(9, 9) и, обладающей тем свойством, что угловой коэффициент любой касательной к ней вдвое меньше углового коэффициента радиус-вектора точки касания. Найти общее решение дифференциального уравнения  Найти общее решение дифференциального уравнения методом вариации произвольных постоянных  . |
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
;
;
.
;
;
.