Статистика Волегов СА. Контрольная работа по дисциплине Статистика в ыполнил Студент Волегов Сергей Андреевич Группа зм111 Екатеринбург
 Скачать 143.88 Kb. Скачать 143.88 Kb.
|
                                                   МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИУРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ контрольная работа по дисциплине «Статистика» Выполнил: Студент Волегов Сергей Андреевич Группа ЗМ-11-1 Екатеринбург 2012 год ОГЛАВЛЕНИЕ
Раздел I. Задания для выполнения контрольной работы по теории статистики Задача 1. Имеются выборочные данные (выборка 5%-ная механическая) по 20 предприятиям за отчетный год:
По исходным данным Вашего варианта:
С вероятностью 0,997 определите ошибку выборки для доли предприятий, находящихся в последней 5-ой группе интервального ряда распределения и границы, в которых будет находиться генеральная доля. Сделайте выводы.
h= xmax - xmin, n где xmax и xmin – максимальные и минимальные значения признака в совокупности n – число групп 1200 1630 - 430 5 = 240 5 = h=
Для построения графиков составим следующую таблицу: Таб.1.1. Распределение числа предприятий по среднегодовой стоимости ОПФ
Рис.1.1. Гистограмма распределения предприятий по среднегодовой стоимости ОПФ 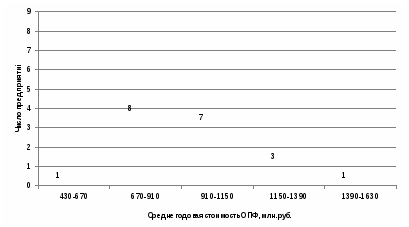 Рис.1.2. Полигон распределения предприятий по среднегодовой стоимости ОПФ 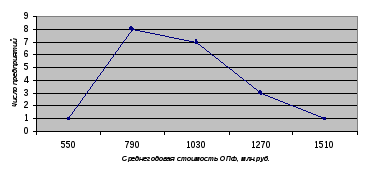 Рис.1.3. Кумулята распределения предприятий по размеру среднегодовой стоимости ОПФ 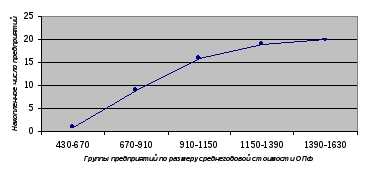 2) Таб. 1.2. Удельный вес предприятий в общем количестве предприятий
3) Определим средний уровень ряда по формуле средней арифметической: f _ x = n где n – число предприятий _ x = 1939 / 20 = 969, 75 Определим средний уровень ряда методом моментов k x - a x - a f f k _ x = f f - момент первого порядка = m1 * k + a, где Таб.1.3.
Из таблицы 1.3. видим, что а – вариант, соответствующий наибольшей частоте – при f=8 равен 790 k=240 Вычисляем момент первого порядка: m1= 15/20 = 0,75 _ x = k m1 + а _ x = 240 * 0,75 + 790 = 180 + 790 = 970 Размах вариации определим по формуле R = xmax - xmin R = 1630 – 430 = 1200 Среднее линейное отклонение найдем по формуле х - хf f đ = Для определения этого и последующих значений составим таблицу Таб. 1.4.
đ = 3720 / 20 = 186 Дисперсию определим по формуле σ2 = k2 (m2 – m12) f x - a k m2 = f m2 = 29 / 20 = 1,45 σ2 = 2402 (1,45 – 0,752) = 57600 * (1,45 – 0,5625) = 57600 * 0,8875 = 51120 Среднее квадратическое отклонение находим по формуле σ = σ2 σ = 51120 = 226,1 Коэффициент вариации Vσ = σ / x * 100 Vσ = 226,1 / 970 * 100 = 23,31 Для определения моды воспользуемся данными таблицы 1.3. f2 – f1 (f2 – f1) + (f2 – f3) Mо = x0 + k где f2 – наибольшая (модальная) частота интервала; f1 – частота интервала, стоящая перед модальным; f3 – частота интервала, последующего за модальным; x0 – начальное значение модального интервала; k – размер модального интервала. 7 8 - 1 Mо = 670 + 240 = 670 + 240 * 0,875 = 880 8 = 670 + 240 (8 - 1) + (8 - 7) Данными той же таблицы воспользуемся для определения медианы Nme – Sm-1 Mе = x0 + k fm Nme = n + 1 2 где fm– частота медианного интервала; Sm-1 – сумма накопленных частот до интервала; xo– начальное значение медианного интервала; k– размер медианного интервала; n – сумма всех частот ряда. Nme= (20 + 1) / 2 = 21 / 2 = 10,5 Медианным является интервал 910-1150 млн.руб., т.к. в этом интервале находятся 10 и 11. Начальное значение медианного интервала 910, его частота – 7, сумма накоплений до него – 9. Ме = 910 + 240 * (10,5 – 9) / 7 = 910 + 240 * 0,214 = 910 + 51,36 = 961,36
(1 – σ2 x = n N ) n σ2 = 51120 n = 20 n/N = 0,05 (из условия что выборка 5%) 51120 x = (1 – 0,05) = 2556 * 0,95 = 2428,2 = 49,277 20 Определим предельную ошибку выборки Δх = tx для P=0,954 t=2 Δх = 2 * 49,277 = 98,554 Определим границы генеральной средней _ _ _ x – Δх ≤ х ≥ x + Δх _ 970 – 98,554 ≤ х ≥ 970 + 98,554 _ 871,446 ≤ х ≥ 1068,554 Количество предприятий в последней группе равняется 1. Соответственно доля этого предприятия в общем количестве предприятий равна W = 1 / 20 = 0,05 Среднюю ошибку выборки для доли определим по формуле n w(1-w) ) N (1 – n w = 0,05(1-0,05) w = (1–0,05) = 0,05(0,95)/20 * 0,95 = 0,002256 = 0,0475 20 Определим предельную ошибку выборки Δw = tw для P=0,997 t=3 Δw = 3 * 0,0475 = 0,1425 Определим границы генеральной средней w – Δw ≤ р≥ w + Δw 0,05 – 0,1425 ≤ р ≥ 0,05 + 0,1425 р ≥ 0,925 Задача 2. Имеется информация о среднедушевых доходах на душу населения по РФ за 2010 год, руб.
Для анализа динамики изучаемого показателя определите: 1) а) в соответствии с классификацией – вид ряда динамики; б) средний уровень ряда; в) цепные и базисные показатели по среднедушевому доходу: абсолютные приросты, темпы (коэффициенты) роста и прироста; г) абсолютное значение 1% прироста. 2) Средние показатели абсолютного прироста, темпов (коэффициентов) роста и прироста. Результаты вычислений представьте в табличной форме (макет таблицы): Макет таблицы Аналитические показатели среднедушевых доходов населения РФ
Сделайте анализ полученных результатов. 3) а) определить линейную форму тренда среднедушевых доходов населения; б) построить график динамики среднедушевых доходов населения за изучаемый период по фактическим и теоретическим данным; в) спрогнозировать среднедушевые доходы населения на 2013 год, используя методы: 1) среднего абсолютного прироста; 2) среднего тема роста; 3) аналитического выравнивания. Сделайте анализ полученных результатов 1) Вид ряда динамики интервальный, т.к. мы рассматриваем среднедушевой доход за определенный период времени. Средний уровень ряда найдем по формуле у = у / n у = 69199 / 5 = 13839,8 Для определения абсолютного прироста, темпов роста и прироста, абсолютного значения % прироста используем следующие формулы - абсолютный прирост цепной Δц = уi – yi-1 где уi – любой уровень ряда, начиная со второго; yi-1 – уровень, непосредственно предшествующий данному - абсолютный прирост базисный Δб= yi – y0 где y0 – уровень первого члена динамического ряда - темп роста цепной Трц = уi / yi-1 * 100 - темп роста базисный Трб = yi / y0 * 100 - темпы прироста Тпр = Тр – 100 - абсолютное значение 1% прироста А = 0,01 yi-1 Результаты представим в таблице Таб. 2.1.
2) Средние показатели _ Δц = Δц / n = 7368 / 5 = 1473,6 _ Δб = Δб / n = 19559 / 5 = 3911,8 _ Трц = Трц / n = 459,95 / 5 = 91,99 _ Трб = Трб / n = 597,007 / 5 = 119,401 _ Тпрц = Тпрц / n = 59,95 / 5 = 11,99 _ Тпрб = Тпрб / n = 97,007 / 5 = 39,401 3) Для определения линейной модели тренда среднедушевых доходов применим аналитическое выравнивание. Для решения составим таблицу. Таб.2.2.
ŷt = a0 + a1t где ŷt – уровни ряда, выравненные по фактору времени; t– период времени; a0 иa1 – параметры прямой. y a0 = n ty a1 = t2 При нечетном числе уровней ряда динамики (у нас их пять) период времени в середине ряда (2008 год) приравниваем к 0, периоды вверх от него (2007 и 2006 г.г.) обозначаем -1 и -2, а вниз (2009 и 2010 г.г.) +1 и +2. Рис. 2.1. Эмпирические и выравненные значения среднедушевого дохода 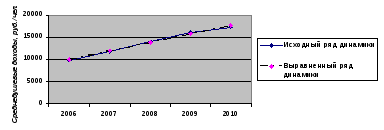 Спрогнозируем среднедушевой доход на 203 год методом аналитического выранивания. ŷt = a0 + a1t ŷt = 13839,8 + 1904,5 * t t = 2 + 3 = 5 (2 – это условная величина 2010 года, 3 – кол-во лет до 2013 года) ŷt = 13839,8 + 1904,5 * 5 = 13839,8 + 95225, = 23362,3 Задача 3. В 2009 г. Среднегодовая численность населения города составляла 1018,3 тыс. чел, в 2010 г. – 1025, 8 тыс. чел, в 2011 г. – 1030, 6 тыс. чел.
а) 102,8 и 101,2; в) 100,7 и 101,2 с) 101,8 и 102,3. 2) Определить в % цепные относительные величины динамики (с точностью до 0,1 %): а) 105,3 и 101, 8; в) 100,7 и 100,5; с) 100,7 и 102,4. 1) Темпы роста базисные определим по следующей формуле Трб = yi / y0 * 100 где уi – любой уровень ряда, начиная со второго; y0 – уровень первого члена динамического ряда Трб = 1025,8 / 1018,3 * 100 = 100,74 Трб = 1030,6 / 1018,3 * 100 = 101,21 Правильный ответ – в. 2) Темпы роста цепные определим по формуле Трц = уi / yi-1 * 100 где yi-1 – уровень, непосредственно предшествующий данному Трц = 1025,8 / 1018,3 * 100 = 100,74 Трц = 1030,6 / 1025,8 * 100 = 100,47 Правильный ответ – в. Задача 4. Дисперсия признака равна (с точностью до 0,1) при условии: средняя величина признака – 22 тыс. руб., коэффициент вариации – 26%: а) 44,5 с) 12,8 в) 32,7 d) 37,2 _ Vσ = σ / x * 100 _ σ = Vσ * x / 100 Vσ = 26% _ х = 22, тыс.руб. σ = 26 * 22 / 100 = 572 / 100 = 5,72 σ2 = 5,722 = 32,7 Правильный ответ – в. Задача 5. Цены на бензин в 4-м квартале текущего года по сравнению с 4-м кварталом предыдущего года возросли на 1 литр с 23 до 27 руб. Каков ежеквартальный темп прироста цен на бензин (в %): а) 8,3 с) 2,9 в) 4,1 d) 10,4 Вычислим коэффициент темпа роста 27/23=1,174 Вычислим средний темп роста 41,174 = 1,041 или 104,1% Ежеквартальный темп прироста равен: 104,1-100=4,1 Правильный ответ – в. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
