контрольная статистика. Контрольная работа по дисциплине Статистика Вариант 2 Выполнила студентка группы
 Скачать 188.35 Kb.
|
|
ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ЖИЛИЩНО-КОМУНАЛЬНОГО ХОЗЯЙСТВА Донецкий институт городского хозяйства Контрольная работа по дисциплине «Статистика» Вариант 2 Выполнила студентка группы ______________ ________________________________________ Руководитель ___________________________ Донецк 2008г. Задача 1 По данным об основных фондах группы промышленных предприятий, за отчетный год, определить: Среднее значение показателя (среднее арифметическое) Показатели вариации (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию, коэффициент вариации) Таблица 1 Исходные данные для задачи 1 Номер предпр Основные фонды, млн.грн Номер предпр Основные фонды, млн.грн Номер предпр Основные фонды, млн.грн Номер предпр Основные фонды, млн.грн Номер предпр Основные фонды, млн.грн 1 2,74 6 2,5 11 0,51 16 2 21 1,78 2 1,47 7 1,26 12 1,18 17 1,04 22 0,89 3 0,76 8 0,64 13 2,18 18 0,44 23 1,66 4 1,35 9 0,58 14 1,1 19 1,87 24 0,82 5 0,68 10 2,32 15 0,35 20 0,96 25 1,56 Решение: Таблица 2. Данные для расчета основных статистических показателей Номер предпр Основные фонды, млн.грн   Номер предпр Основные фонды, млн.грн 1 2,74 1,43 2,06 14 1,1 0,21 0,04 2 1,47 0,16 0,03 15 0,35 0,96 0,91 3 0,76 0,55 0,30 16 2 0,69 0,48 4 1,35 0,04 0,00 17 1,04 0,27 0,07 5 0,68 0,63 0,39 18 0,44 0,87 0,75 6 2,5 1,19 1,43 19 1,87 0,56 0,32 7 1,26 0,05 0,00 20 0,96 0,35 0,12 8 0,64 0,67 0,44 21 1,78 0,47 0,23 9 0,58 0,73 0,53 22 0,89 0,42 0,17 10 2,32 1,01 1,03 23 1,66 0,35 0,13 11 0,51 0,80 0,63 24 0,82 0,49 0,24 12 1,18 0,13 0,02 25 1,56 0,25 0,06 13 2,18 0,87 0,76 сумма 32,64 14,14 11,14 Среднее значение показателя  , где - отдельные значения изучаемого показателя;n – количество значений показателя.  Размах вариации  , где - максимальное и минимальное значение показателя Среднее линейное отклонение   Дисперсия   Среднее квадратическое отклонение  Коэффициент вариации статистического ряда  Т.к. Vx > 15%, то совокупность неоднородная. Задача 2 По статистическим данным об объеме производства важнейших видов продукции в Украине в 1987-1992 гг., выполнить следующее: определить уровни ряда динамики по периодам времени, приняв за базисный период 1987г., а затем: а) поместить значения уровней динамики в таблицу; б) изобразить ряд динамики графически. 2) определить базисные и цепные абсолютные приросты объема продукции; 3) определить базисные и цепные коэффициенты и темпы роста (динамики); 4) определить базисные и цепные темпы прироста; 5) определить абсолютное значение одного процента прироста объема продукции; 6) определить средний уровень ряда динамики; 7) определить средний темп роста и средний темп прироста объема продукции; 8) определить среднюю величину 1% прироста объема продукции. Решение 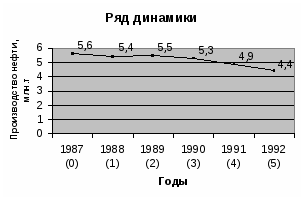 1. Данные по нефтиТаблица 3. Исходные данные для задачи 2. Годы Нефть, млн.т 1987 (0) 5,6 1988 (1) 5,4 1989 (2) 5,5 1990 (3) 5,3 1991 (4) 4,9 1992 (5) 4,4 2. Абсолютный прирост а) базисный   и т.д. б) цепной  и т.д. 3. Коэффициент роста: а) базисный   и т.д. б) цепной  и т.д. 4. Определяем темп роста а) базисный   и т.д. б) цепной  и т.д. 5. Темп прироста: а) базисный   и т.д. б) цепной  и т.д. Абсолютное значение 1% прироста   млн.т млн.ти т.д. Занесем полученные данные в таблицу Таблица 4. Показатели 1987 (0) 1988 (1) 1989 (2) 1990 (3) 1991 (4) 1992 (5) Уровень нефти, млн.т 5,6 5,4 5,5 5,3 4,9 4,4 Абсолютный прирост, млн.т -базисный 0 -0,2 -0,1 -0,3 -0,7 -1,2 -цепной 0 -0,2 0,1 -0,2 -0,4 -0,5 Коэффициент роста -базисный 0 0,964 0,982 0,946 0,875 0,786 -цепной 0 0,964 1,019 0,964 0,925 0,898 Темпы роста, % -базисный 0 96,4% 98,2% 94,6% 87,5% 78,6% -цепной 0 96,4% 101,9% 96,4% 92,5% 89,8% Темпы прироста, % -базисный 0 -3,57% -1,79% -5,36% -12,50% -21,43% -цепной 0 -3,57% 1,85% -3,64% -7,55% -10,20% Абсолютная величина 1% прироста, млн.т. 0 0,056 0,054 0,055 0,053 0,049 Средний уровень ряда динамики  Средний темп роста  Средний темп прироста  Среднюю величину 1% прироста   Задача 3 Распределение рабочих машиностроительного завода по уровню заработной платы по данным 10%-го случайного бесповоротного выборочного обследования Таблица 5 Исходные данные для задачи 3. Зарплата, грн Число рабочих, чел. 100-200 16 200-300 48 300-400 30 400-500 28 500-600 20 600-700 8 Итого 150 Определить: 1) размер средней заработной платы завода (с вероятностью 0,683); 2) долю рабочих завода, имеющих заработную плату на уровне средней и выше (с вероятностью 0,997); 3) необходимую численность выборки при определении средней заработной платы, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5 грн; 4) необходимую численность выборки при определении доли рабочих , имеющих заработную плату на уровне средней и выше, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5%. Решение Составим расчетную таблицу Таблица 6 Расчетная таблица Зарплата, грн Число рабочих (f) Середина интервала (x)     100-200 16 150 2400 -208 43264 692224 200-300 48 250 12000 -108 11664 559872 300-400 30 350 10500 -8 64 1920 400-500 28 450 12600 92 8464 236992 500-600 20 550 11000 192 36864 737280 600-700 8 650 5200 292 85264 682112 Итого 150 53700 2910400 Размер средней заработной платы рабочих завода составит  Предельная ошибка определения средней зарплаты с вероятностью 0,683  , гдеt – коэффициент доверия, при заданной вероятности 0,683; t=1  - средняя ошибка выборочной средней при бесповторном случайном методе отбора единиц в выборочную совокупность , где - дисперсия показателя;n- численность единиц наблюдения в выборочной совокупности измерения; n=150 N-численность единиц в генеральной совокупности; при 10% выборке N=1500 чел. Дисперсия 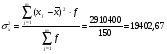 Предельная ошибка  Средняя заработная плата с вероятностью 0,683, ожидается в пределах   Доля рабочих завода, имеющих заработную плату на уровне средней и выше определим  , где - конец интервала, включающего среднее значение х; - величина интервала, включающего среднее значение х; - частота величина интервала, включающего среднее значение х;S – сумма частот, накопленных после интервала, включающего среднее значение х;  Предельная ошибка определения доли рабочих, имеющих заработную плату на уровне средней и выше, с вероятностью 0,997  , гдеt – коэффициент доверия, при заданной вероятности 0,997; t=3  , гдеp- доля единиц выборочной совокупности, обладающих некоторым признаком ( в нашем случае доля рабочих с зарплатой на уровне средней и выше р=0,53)  Доля рабочих с заработной платой на уровне средней и выше с вероятностью 0,997 ожидается в пределах  0,46 - 0,12 = 0,34 = 0,46 + 0,12 = 0,58Необходимая численность выборки при определении средней заработной платы, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5грн.  Коэффициент доверия при вероятности 0,954 составит t=2 Предельная ошибка выборки по условию  Дисперсия   Необходимая численность выборки при определении доли рабочих, имеющих зарплату на уровне средней и выше, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5%  Задача 4 По данным 10%-го выборочного обследования рабочие-многостаночники машиностроительного завода распределены по проценту выполнения норм выработки за месяц. Таблица 7 Исходные данные для задачи 4. Процент выполнения норм выработки Число рабочих цеха №1 Число рабочих цеха №2 80-100 2 3 100-120 4 4 120-140 6 5 140-160 11 6 160-180 4 3 180-200 1 3 200-220 2 1 Итого 30 25 Определить групповые дисперсии; Внутригрупповую дисперсию; Межгрупповую дисперсию средних; Общую дисперсию; Корреляционное отношение. По результатам вычислений оценить силу влияния фактора группировки. Решение Составим таблицу для расчетов Таблица 8 Процент выполнения норм выработки Число рабочих, чел f Середина интервала, x 80-100 2 90 180 -54,667 2988,44 5976,89 100-120 4 110 440 -34,667 1201,78 4807,11 120-140 6 130 780 -14,667 215,111 1290,67 140-160 11 150 1650 5,33333 28,4444 312,889 160-180 4 170 680 25,3333 641,778 2567,11 180-200 1 190 190 45,3333 2055,11 2055,11 200-220 2 210 420 65,3333 4268,44 8536,89 Итого 1 группе (1 цех) 30 4340 25546,7 80-100 3 90 270 -52 2704 8112 100-120 4 110 440 -32 1024 4096 120-140 5 130 650 -12 144 720 140-160 6 150 900 8 64 384 160-180 3 170 510 28 784 2352 180-200 3 190 570 48 2304 6912 200-220 1 210 210 68 4624 4624 Итого 2 группе (2 цех) 25 3550 27200 Средний процент выполнения норм выработки по каждой группе рабочих     Групповые дисперсии 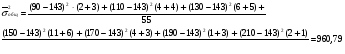    Внутригрупповая дисперсия 959,03Межгрупповая дисперсия   Общая дисперсия  Коэффициент детерминации  Корреляционное отношение  Коэффициент детерминации показывает, что вариация процента выполнения нормы выработки обусловлена вариацией цехов завода лишь на 0,18%. Корреляционное отношение, равное 0,04, показывает что доля данной группы рабочих связь между цехами и процентом выполнения нормы выработки незначительная, т.е. фактор группировки в данном случае оказывает незначительное влияние. Задача 5 Дано данные об использовании времени рабочих за IV квартал (92 календарных дня, в том числе 66 рабочих дней и 26 праздничных и выходных). По данным таблицы 9 определить: Календарный, табельный и максимально возможный фонд рабочего времени. Среднесписочное число рабочих за квартал Среднее явочное число рабочих. Коэффициент использования числа рабочих дней. Коэффициент использования продолжительности рабочего дня с учетом того, что удельный вес рабочих с 36-часовой рабочей неделей составляет 10%, с 40-часовой – 90% Интегральный показатель использования рабочего времени По таблице 10 определить Относительные показатели оборота рабочих по приему и выбытию за предшествующий и отчетный периоды. Показатели текучести рабочей силы за предшествующий и отчетные годы. Сопоставить полученные данные и сделать выводы. Таблица 9 Отчетные данные об использовании рабочего времени на предприятии Показатели Отработано чел.дней 44500 Целодневные простои 11 Очередные отпуска 1900 Отпуска в связи с родами 330 Болезни 1980 Прочие неявки, разрешенные законом 550 Прогулы 11 Праздничные и выходные 19900 Отработано чел.час 336000 В т.ч. сверхурочно 5400 Внутрисменные простои 385 Таблица 10 Отчетные данные о движении рабочей силы Показатели Предшествующий год Отчетный год Принято на предприятие рабочих 187 50 Выбыло с предприятия рабочих 254 70 В т.ч. переведено на другие предприятия 10 - В т.ч. уволено в связи с окончанием работ и срока договора 20 5 В т.ч. уволено в связи с переходом на учебу 50 10 В т.ч. уволено в связи с уходом в армию 15 5 В т.ч. уволено в связи с уходом на пенсию 10 - В т.ч. уволено по собственному желанию 139 42 В т.ч. уволено за прогулы и нарушения труд.дисциплины 10 8 Среднесписочное число рабочих 1280 1250 Решение: Календарный фонд рабочего времени Таблица 11 Отработано чел.дней 44500 Целодневные простои 11 Праздничные и выходные 19900 Число неявок, в т.ч. Очередные отпуска 1900 Отпуска в связи с родами 330 Болезни 1980 Прочие неявки, разрешенные законом 550 Прогулы 11 Итого календарный фонд, чел.дней 69182 Табельный фонд  Максимально возможный  Среднесписочное явочное количество рабочих  Среднее явочное число рабочих  Коэффициент использования числа рабочих дней    Коэффициент использования продолжительности рабочего дня, 36час – 10% ставка, 40 час – 90% ставка  С учетом сверхурочных  7,56час/дни  Урочные   Интегральный коэффициент использования рабочего времени  с учетом сверхурочных  без учета сверхурочных  Относительные показатели оборота рабочих по приему и выбытию за предшествующий и отчетный периоды. Оборот кадров по приему:  Текущий год  Предыдущий год  Оборот кадров по выбытию  Показатели текучести рабочей силы за предшествующий и отчетные годы.  Предшествующий год  или 11,6%Отчетный год  или 4%Вывод: Текучесть рабочей силы за отчетный год меньше, чем за предшествующий на 7,6%. Оба коэффициента текучести указывают на высокую текучесть кадров. |