арх. Контрольная работа по курсу Архитектура Вычислительных Систем

• Название: Контрольная работа по курсу Архитектура Вычислительных Систем
• Дата: 28.05.2022
• Размер: 0.85 Mb.
• Имя файла: арх.doc
• Тип: Контрольная работа; #554537
• страница: 3 из 3

III Раздел – Организация операционных устройств и процессоров

8. 
   Построить схемы и временные диаграммы умножения двух 4-разрядных чисел на процедурном умножителе (косвенное умножение)
   

P = M x K, где M = (N mod 15) + 1, K = (N mod 7) + 1.
Синтезировать схему одной ячейки ОЗУ адресного типа с прямым доступом для устройства типа 3D на RS-триггерах.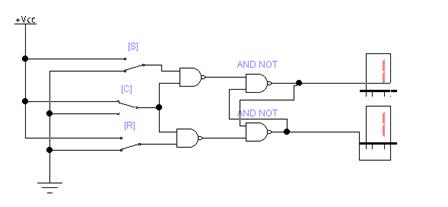



Синхронный RS триггер

Сложность схемы: С=4Слэ, Время задержки: t=2tлэ.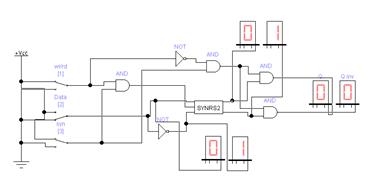



Сложность схемы: С=10Слэ, Время задержки: t=6tлэ.

Синтезировать схему запоминающего устройства на базе ячейки, полученной в п.1, типа 3D на RS-триггерах с организацией 5х2.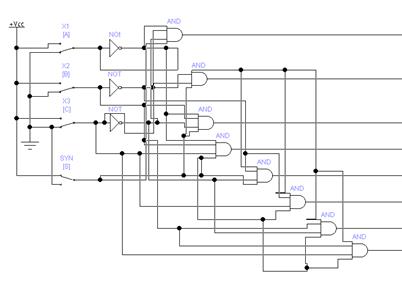



Схема дешифратора DCX

Сложность схемы: С=35Слэ, Время задержки: t=4tлэ.

Таблица 3. Таблица истинности дешифратора DCX

x1	x2	x3	dcx0	dcx1	dcx2	dcx3	dcx4	dcx5	dcx6	dcx7
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

 



Схема дешифратора DCY

Таблица 4. Таблица истинности DCY

x1	x2	dcy0	dcy1
1	0	1	0
0	1	0	1

 

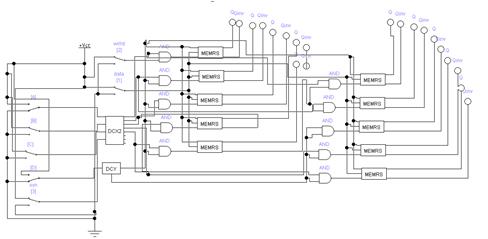Схема массива ячеек памяти типа 3D 5x2

Сложность схемы: С=10Сmem+CDCX+CDCY +10Сand=10*10Слэ+35Cлэ+Cлэ+ 10Cлэ =146Слэ, Время задержки: t=tDCX+tmem + tDCY =11tлэ.

На базе ЗУ, полученного при выполнении предыдущего задания, синтезировать схему ЗУ вдвое большего объема (с удвоенным количеством адресуемых слов). Реализовать 2 варианта:

а) дополнительный бит адреса является старшим;

б) дополнительный бит адреса является младшим (расслоение памяти).

а) дополнительный бит адреса является старшим: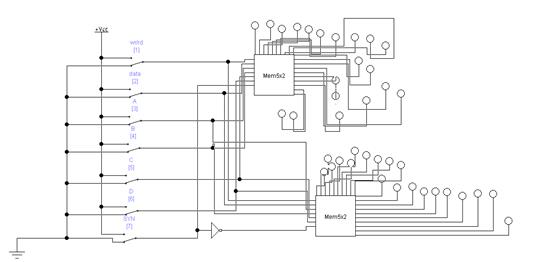



Удвоение массива для варианта а)

Сложность схемы: С=2СMem5x2+Слэ=2*146+1=293Слэ, Время задержки: t=tлэ+tMem5x2=11+1=12tлэ.

б) дополнительный бит адреса является младшим (расслоение памяти):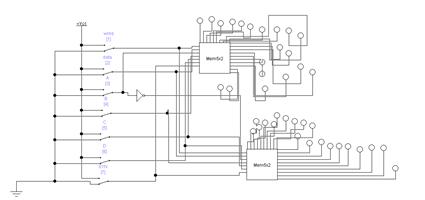



Удвоение массива для варианта б)

Сложность схемы: С=2СMem5x2+Слэ=2*146+1=292Слэ, Время задержки: t=tлэ+tMem5x2=11+1=12tлэ.

9. 
   Построить схемы и временные диаграммы умножения двух 6-разрядных чисел на матричном умножителе Брауна
   

P = M x K, где M = (N mod 15) + 1, K = (N mod 7) + 1.
Синтезировать схему одной ячейки ОЗУ адресного типа с прямым доступом для устройства типа 3D на RS-триггерах.



Синхронный RS триггер

Сложность схемы: С=4Слэ, Время задержки: t=2tлэ.



Сложность схемы: С=10Слэ, Время задержки: t=6tлэ.

Синтезировать схему запоминающего устройства на базе ячейки, полученной в п.1, типа 3D на RS-триггерах с организацией 5х2.



Схема дешифратора DCX

Сложность схемы: С=35Слэ, Время задержки: t=4tлэ.

Таблица 3. Таблица истинности дешифратора DCX

0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

 



Схема дешифратора DCY

Таблица 4. Таблица истинности DCY

x1	x2	dcy0	dcy1
1	0	1	0
0	1	0	1

 

Схема массива ячеек памяти типа 3D 5x2

Сложность схемы: С=10Сmem+CDCX+CDCY +10Сand=10*10Слэ+35Cлэ+Cлэ+ 10Cлэ =146Слэ, Время задержки: t=tDCX+tmem + tDCY =11tлэ.

На базе ЗУ, полученного при выполнении предыдущего задания, синтезировать схему ЗУ вдвое большего объема (с удвоенным количеством адресуемых слов). Реализовать 2 варианта:

а) дополнительный бит адреса является старшим;

б) дополнительный бит адреса является младшим (расслоение памяти).

а) дополнительный бит адреса является старшим:



Удвоение массива для варианта а)

Сложность схемы: С=2СMem5x2+Слэ=2*146+1=293Слэ, Время задержки: t=tлэ+tMem5x2=11+1=12tлэ.

б) дополнительный бит адреса является младшим (расслоение памяти):



Удвоение массива для варианта б)

Сложность схемы: С=2СMem5x2+Слэ=2*146+1=292Слэ, Время задержки: t=tлэ+tMem5x2=11+1=12tлэ.

Лабораторная работа № 3. Исследование операционных устройств для выполнения умножения

Цель работы: В данной работе исследуются операционные устройства для выполнения умножения беззнаковых чисел (модулей). Рассматриваются устройства двух типов: процедурного типа для реализации косвенного умножения (с жесткой логикой управления) и структурного типа (с жесткой структурой) для аппаратной реализации вычислений на примере матричного умножителя Брауна и древовидного умножителя Уоллеса. На примере косвенного умножителя изучаются принципы построения управляющих цифровых автоматов.

Порядок выполнения работы:

Построить схему матричного умножителя Брауна для умножения двух чисел в заданной разрядности.

Матричный умножитель Брауна, для умножения двух двухразрядных чисел.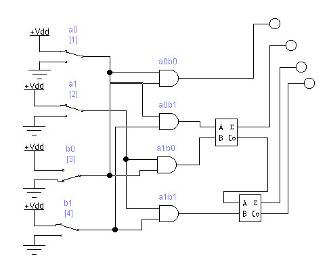



Время задержки: Tумн = t + (n + m - 2)*tsm,

где n - разрядность множимого, m - разрядность множителя.

Для 2-х разрядных чисел: Tумн=3*t.

Сложность схемы: С=4Слэ+2Сsm=8Слэ.

Модифицировать схему из предыдущего задания, добавив необходимое количество фиксаторов для организации конвейера.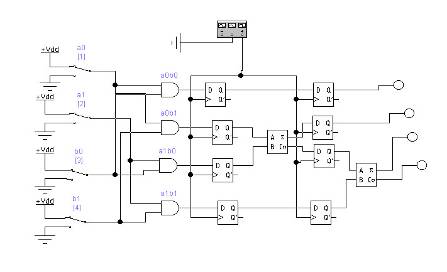



Время задержки: Tумнк = 3*(tsm+ tff) + t=11*t

Сложность схемы: С=40Слэ.

Построить схему сумматора с сохранением переноса для сложения заданного числа слагаемых заданной разрядности.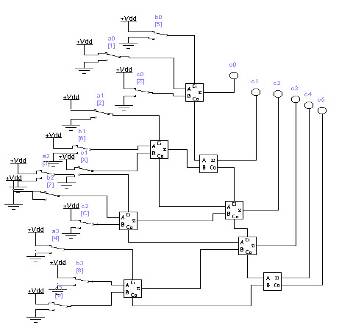



Сложность схемы: С=8СSM=8*5=40Слэ, Время задержки: t=4*tSM=4*3=12tлэ.

Построить схему умножителя Уоллеса на базе ССП из предыдущего пункта.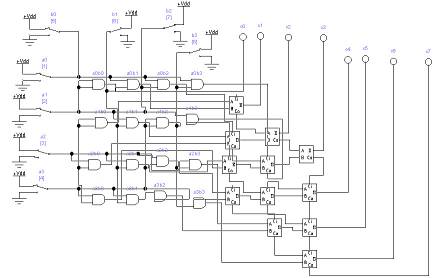



Сложность схемы: С=16Слэ+12Csm=76Cлэ. Время задержки: t=13tлэ.

Построить схему конвейерного умножителя Уоллеса.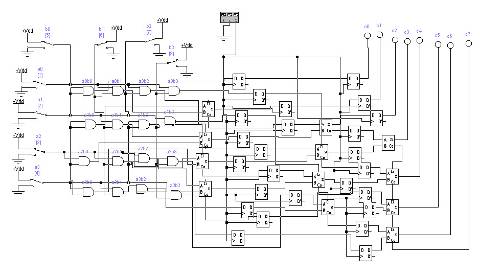



Сложность схемы: С=16Слэ+12Csm+28Стр=188Cлэ. Время задержки: t=21tлэ

10. 
    Построить схемы и временные диаграммы умножения двух 6-разрядных чисел на древовидном умножителе Уоллеса
    

P = M x K, где M = (N mod 15) + 1, K = (N mod 7) + 1.
При аппаратном способе умножение выполняется устройством согласно заложенного в него алгоритма после подачи операндов А и В на его входы. Аппаратные умножители строятся на основе комбинационных устройств. Они обладают наибольшим быстродействием. Ниже рассматриваются матричные умножители двоичных чисел.

Общие принципы построения матричных умножителей. Принцип построения комбинационного умножителя М х N разрядов вытекает из правила умножения двоичных чисел: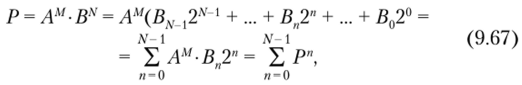



где А^м = А_м_ ,2^м-' + ...+ А_т2 “+ ... + А₀2° - множимое; В^х = В_х ,2^Л' ¹ + + ... + В_п2"+ ... + В₀2° — множитель; Р" = А^м В_п2^п — частичное произведение.

Заметим, что разрядность операндов обозначается верхними индексами, так как нижние индексы используются для нумерации отдельных разрядов, начиная с 0.

Правило умножения иллюстрируется примером для случая М = 4, N=2 на рис. 9.88.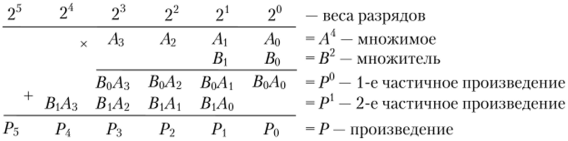



Рис. 9.88. Иллюстрация правила умножения двоичных чисел

Операция арифметического умножения двух одноразрядных двоичных чисел совпадает с операцией логического умножения, т.е.



Поэтому члены В_пА_т, где п = 0,..., ЛГ- 1; т = 0,..., М- 1, вырабатываются одновременно с помощью конъюнкторов (рис. 9.89). Их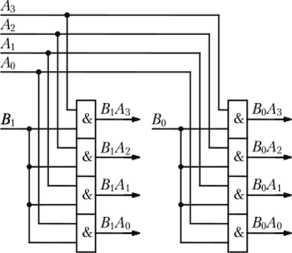



Рис. 9.89. Схема формирования произведений В_пА_т для умножителя 4X2

сложение в столбцах может быть выполнено различными способами. Рассмотрим один из возможных способов. Для этого запишем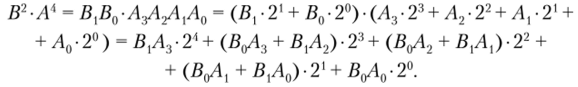



Для суммирования выражений в скобках можно использовать неполные одноразрядные сумматоры, представляя результаты в виде суммы текущего разряда и переноса в следующий разряд:



С помощью неполного сумматора сложим сумму с переносом С₂, вес которых составляет 2²:

(вес суммы 5| — 2², переноса С% — 2³).

Теперь, используя полный одноразрядный сумматор, складываем сумму 5з и два переноса С₃, С², имеющие вес 2³:

(вес суммы 5² — 2³, переноса С — 2⁴).

И наконец, с помощью полного одноразрядного сумматора осуществляем сложение оставшегося члена В,Л₃ и двух переносов С, С с весом 2⁴:

(вес суммы 5₄ — 2⁴, переноса С₅ — 2⁵).

На этом процесс суммирования заканчивается, так как нс осталось ни одного члена вида В,Д„ и ни одного переноса С- (/ < 5) одноразрядных сумматоров младших разрядов. Организация суммирования в умножителе 4 х 2 с использованием одноразрядных сумматоров показана на рис. 9.90. На основании рис. 9.90 нс составляет труда построить схему умножителя 4x2.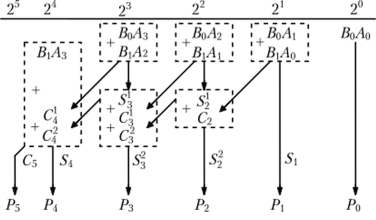



Для большей наглядности вместо общепринятого обозначения одноразрядного сумматора (рис. 9.91, а) будем использовать обозначение, приведенное на рис. 9.91, б. При этом следует учитывать, что неполный сумматор не имеет входа переноса С₀. Схема умножителя 4x2 без набора конъюнкторов изображена на рис. 9.91, в. Как ясно из рис. 9.91, в, схема умножителя имеет матричную структуру. Умножители двоичных чисел такого типа называют множительными блоками.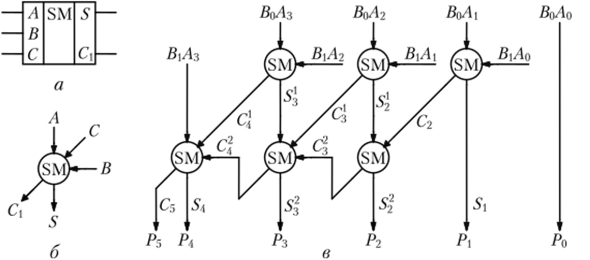



Построение умножителей на большее число разрядов с помощью множительных блоков требует дополнительных схем, называемых деревьями Уоллеса. Такие микросхемы имеются только в зарубежных сериях. От указанного недостатка свободны множительно- суммирующие блоки.