Математические методы в геологии. Контрольная работа по математическим методам в геологии

• Название: Контрольная работа по математическим методам в геологии
• Дата: 24.10.2022
• Размер: 301 Kb.
• Имя файла: Математические методы в геологии.doc
• Тип: Контрольная работа; #751824
• страница: 3 из 3

2. ПАРНАЯ КОРРЕЛЯЦИЯ

Оценка связи между двумя признаками осуществляется с по­мощью корреляционного отношения и коэффициента корре­ляции.

Корреляционным отношением ή называется отношение ме­ры рассеяния условных средних зависимой переменной к ме­ре рассеяния всех значений зависимой переменной, то есть ή =(y_i) : (y), где у—значения, принимаемые зависимой переменной; y_i — условные средние, соответствующие значе­ниям x_i. По выборочным данным вычисляют выборочное кор­реляционное отношение

 =S(y_i) : S(y)

З 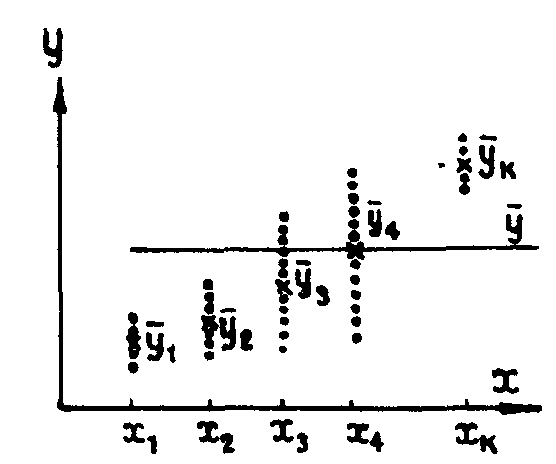начение  изменяется от 0 до 1. Равенство =0—необхо­димое и достаточное условие отсутствия корреляционной за­висимости. При r=1 корреляционная связь переходит в функциональную s(y_i)=s(y), когда все значения перемен­ной, соответствующие определенному x_i, совпадают с y_i, то есть каждому конкретному значению x_i соответствует одно­единственное y_i (рис. 1). Равенство s(y_i)=0 возможно, когда все y_i=y, то есть лежат на одной линии (аргумент из­меняется, функция не реагирует, связи нет).

К
оэффициент корреляции вычисляется по формуле:

и

Рис. 1. Разброс значений зави­симой переменной у и ее ус­ловных средних у

представляет собой правильную дробь, изменяющуюся от —1 до +1. При r > 0 зависимость прямая, при r < 0 — об­ратная, r = 0 свидетельствует об отсутствии линейной связи, но не является показателем независимости Х и Y. При |r|==1 между Х и Y устанавливается линейная функциональная за­висимость вида у=ах+b. Доказано, что всегда  ≥|r|. Ра­венство  = | r | имеет место только в случае, когда зависи­мость между Х и Y линейная, то есть это равенство может служить простейшим критерием линейности зависимости Х и Y. Более строгая оценка линейности связи — критерий t = k : _k, где k=² - r² — мера криволинейности - _k — ошибка k, вычисляемая по формуле :





Если t_эмп < t_ связь может быть признана линейной. Последова­тельность вычислительных операций при определении коэф­фициента корреляции покажем на примере.

Пример. Результаты анализа 15 проб руды на эле­менты Х и Y приведены в табл. 1 (колонки 1, 2). Не­обходимо установить, существует ли линейная связь между изменениями содержания элементов в рудах?

Таблица 1

xi	yi	xi-x	yi-y	(xi-x)2	(yi-y)2	(xi-x)(yi-y)
0.1	1.1	-0.3	-2.0	0.09	4.00	0.60
0.6	4.4	0.2	1.3	0.04	1.69	0.26
0.4	2.3	0	-0.8	0	0.64	0
0.5	3.9	0.1	0.8	0.01	0.64	0.08
0.2	1.5	-0.2	-1.6	0.04	2.56	0.32
0.3	2.2	-0.1	-0.9	0.01	0.81	0.09
0.4	2.6	0	-0.5	0	0.25	0
0.5	4.2	0.1	1.1	0.01	1.21	0.11
0.2	1.9	-0.2	-1.2	0.04	1.44	0.24
0.7	5.5	0.3	2.4	0.09	5.76	0.72
0.4	2.9	0	-0.2	0	0.04	0
0.3	2.4	-0.1	-0.7	0.01	0.49	0.07
0.5	4.2	0.1	1.1	0.01	1.21	0.11
0.3	2.6	-0.1	-0.5	0.01	1.25	0.05
0.6	4.8	0.2	1.7	0.04	2.89	0.34
6.0	46.5			0.40	23.88	2.99

На основе суммарных значений по колонкам 1, 2, 5, 6, 7 имеем: х=6,0: 15==0,4; у=46,5: 15=3,1; s(x)= 10,40: 14=0,17; s (у) =123,88 : 14 = 1,31; r_xy= 2,99: (14 x 0,17 x 1,31) = 0,96.

Д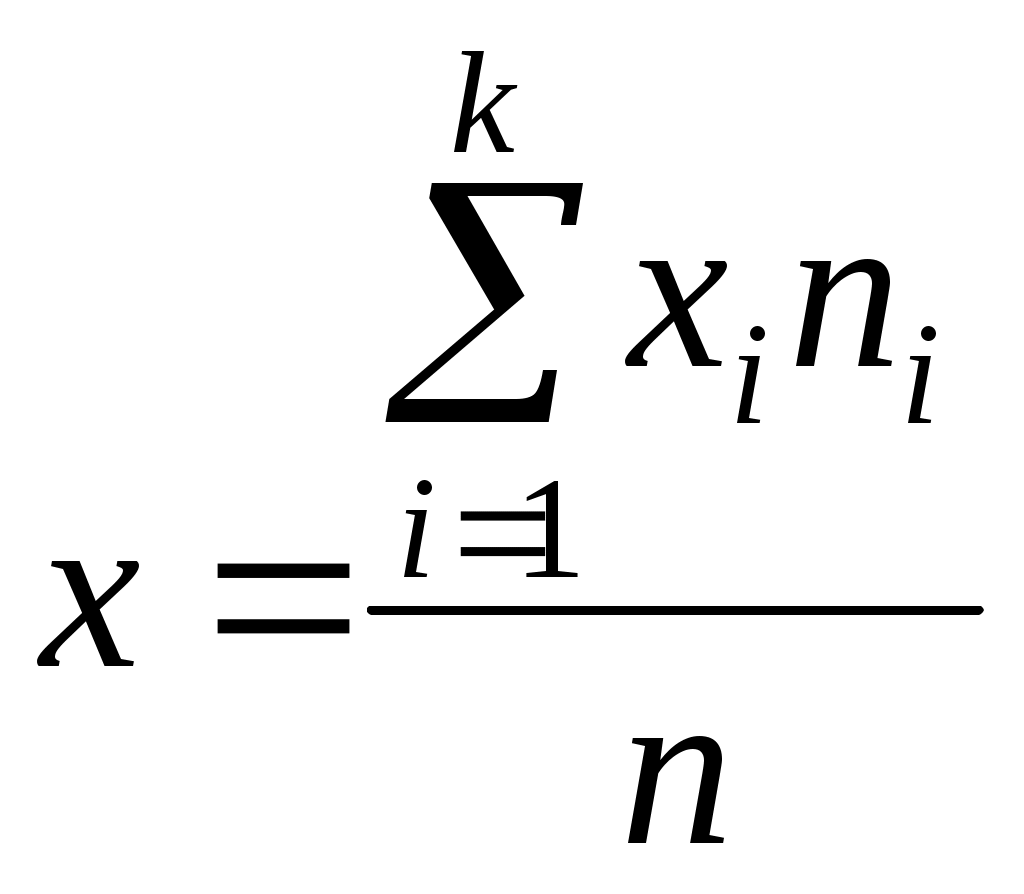
ля вычисления корреляционного отношения необходимо сгруппировать исходные данные по значениям независимой переменной и применить формулу:

Для расчетов удоб­нее пользоваться следующими формулами вычисления квад­ратичных отклонений:
которые следуют из четвертого свойства дисперсии. Расчет корреляционного отношения показан в табл. 2. Таблица 2

xi	Cодержание, yi	yi	ni	yi	yi2	yi2ni
0.1	1.1	1.1	1	1.1	1.21	1.21
0.2	1.5 1.9	3.4	2	1.7	2.89	5.78
0.3	2.2 2.4 2.6	7.2	3	2.4	5.76	17.28
0.4	2.3 2.6 2.9	7.8	3	2.6	6.76	20.28
0.5	3.9 4.2 4.2	12.3	3	4.1	18.81	50.43
0.6	4.4 4.8	9.2	2	4.6	21.16	42.32
0.7	5.5	5.5	1	5.5	30.25	30.25
						167.55

Н
а основе полученной суммы имеем:

(вычислено ранее); = 1,26 : 1,31 = 0,96. Так как получен­ные значения r и  равны между собой и близки к единице, то можно утверждать, что связь между содержаниями эле­ментов Х и Y в изучаемых рудах тесная, линейная.

М
ерой рассеяния r и  служат их основные ошибки, вы­числяемые по формулам:
Значимость коэффициента корреляции определяется кри­терием t = r : _r. Если вычисленное r_эмп больше табличного f = n—2, то коэффициент корреляции значимый. Аналогично определяется значимость корреляци­онного отношения.

П ример. На основании обработки данных получено значение коэффициента корреляции, равное 0,80. Ко­личество проб 55. Определить, является ли полученный коэффициент значимым?

Ошибка t=0,80 : 0,10 >8. Полученная величина больше табличной, следова­тельно, коэффициент корреляции является значимым.

Основные ошибки коэффициента корреляции и корреля­ционного отношения позволяют определить доверительные интервалы для соответствующих параметров r и  (в случае нормальности распределений):

r
- t__rrr+t__r; -t__+t__

Пример. Определить доверительный интервал ко­эффициента корреляции, если r=0,80 и _r=0,03, приняв =0,05.

Имеем: 0,80—1,96 х 0,10  r  0,80+l,96 x 0,10 или 0,60  r  1,00.

Д
ля оценки достоверности коэффициента корреляции, су­щественности различия двух его значений, а также для пост­роения доверительного интервала более надежно пользовать­ся критерием Фишера. Для вычисленного значения r определяют величину

г
де z — случайная величина, распределение которой близко к нормальному. Ошибка z оценивается по формуле
то есть зависит только от объема выборки. Критерий надеж­ности z — t = z : _z. При t_эмп>t_, r значимо.

Доверительный интервал для коэффициента корреляции с помощью величины z находят следующим образом. По z и _z определяют значения z_i=z— t__z и z₂=z+ t__z, на основе которых по табличным данным определяют соответствую­щие им значения r₁ и r₂, являющиеся доверительными гра­ницами для r, то есть r₁  r  r₂.

Пример Определить доверительный интервал для коэффициента корреляции r = 0,80 при n = 55.

П
риняв  = 0,05, находим, что r = 0,80 соответствует величина z= 1,099. При имеющем­ся числе данных: _z = 1 : 52=0,139, z₁= 1,099 — 2,0 x 0,139=0,821; z₂=1,099+2,0 x 0,139 = 1,377. По полу­ченным значениям z₁ и z₂ находим граничные значения коэффициента корреляции 0,68  r  0,88. Величину z можно использовать для проверки существен­ности различия двух выборочных коэффициентов корреля­ции. Ошибка разности
где n₁ и n₂ — объемы выборок, для которых вычислены значения r₁ и r₂. Если величина t=|z₁—z₂| : _z1-z2 больше t(f), то с вероятностью р =1— можно утверждать, что различие между r₁ и r₂ значимое.

Пример. В результате статистической обработки дан­ных по содержаниям меди и никеля в двух типах руд (сливных и вкрапленных) получены коэффициенты кор­реляции 0,75 и 0,60. Количество проб сливных руд 28, вкрапленных 53. Существенно ли различаются руды по тесноте связи между элементами медь—никель?

Д
ля r₁=0,75, z₁= 0,973; для r₂ = 0,60, z₂ =0,693. Основная ошибка

t= |0,973—0,693| : 0,245 =1,1. Табличное значение t_0,05(78)=l,99 по тесноте связи ме­жду содержаниями меди и никеля изучаемые руды не различаются (нет основания говорить о различии на ос­нове имеющихся данных).

О 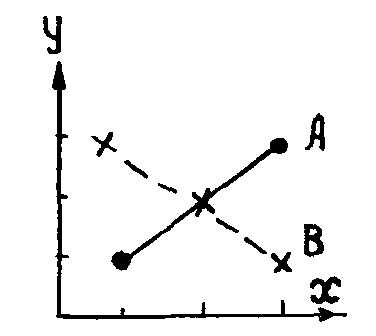ценка тесноты связи может использоваться для сравне­ния выборок. Допустим, имеются данные о содержаниях двух элементов в сравниваемых породах: массив А элемент Х=1, 2, 3 и элемент Y=1, 2, 3; массив В, соответственно, 1, 2, 3 и 3, 2, 1. Для приведенных данных все статистические парамет­ры одинаковы и р
Рис. 2. Линии зависимостей между содержаниями сравниваемых по­родах: А — прямая; В — обратная

азличить породы невозможно. В то же вре­мя видно, что в породах массива А с увеличением содержа­ний одного элемента увеличивается и содержание другого, то­гда как в породах массива В уменьшается (рис. 2). Для — в массива А имеем прямую, для массива В обратную связь между содержаниями изучаемых элементов. За счет перехода к двумерной модели два неинформативных признака, образо­вали один информативный признак характера связи.

Использованная литература

1. 
   Шестаков Ю.Г. Математические методы в геологии. Красноярск., 1988
   
2. 
   Каждан А.Б. , Гуськов О.И., Шимансмкий А.А. Математическое моделирование в геологии и разведке полезных ископаемых. М.; Недра, 1979.
   
3. 
   Бондаренко В.Н. Сравнительный анализ геологических объектов с закономерной изменчивостью свойств. М.; Недра, 1978