Математические методы в геологии. Контрольная работа по математическим методам в геологии

• Название: Контрольная работа по математическим методам в геологии
• Дата: 24.10.2022
• Размер: 301 Kb.
• Имя файла: Математические методы в геологии.doc
• Тип: Контрольная работа; #751824
• страница: 1 из 3

Контрольная работа

по

математическим методам

в геологии

Якутск 2001

Содержание
стр.

1.	СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ	3
2.	ПАРНЫЕ КОРРЕЛЯЦИИ	17
	Использованная литература	23

1. СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И КРИТЕРИИ ИХ ПРОВЕРКИ
Рассмотрим некоторые ситуации, возникающие при стати­стической обработке геологических данных.

1. Одно из значений изучаемой величины резко отлича­ется от основной массы данных. Принадлежит ли последнее значение изучаемой совокупности или оно является следстви­ем включения в выборку случайной пробы других пород, ошибкой анализа, переписи и т. п.?

2. В результате обработки данных по двум выборкам получены различные значения среднего содержания. Является ли полученное различие выборочных средних следствием ре­ального различия изучаемых явлений (объектов) или носит случайный характер?

3. Обработка данных изучаемой величины в пределах двух участков выявила различные значения дисперсий. Свидетель­ствует ли это о различии изучаемых участков по изменчиво­сти величины?

4. Получено различие частостей появления определенных значений изучаемого признака в двух массивах данных. Сви­детельствует ли это о реальном различии распределений изу­чаемого признака для изучаемых явлений (объектов)?

Во всех приведенных примерах необходимо решить вопрос о том, являются ли полученные различия статистик отражением реального различия изучаемых совокупностей или носят случайный характер? Для решения этого вопроса разработан ряд критериев, позволяющих в каждом конкретном случае оценить, существенно полученное различие или случайно. В каждом из таких случаев задача сводится к проверке гипотезы об отсутствии различия сравниваемых статистик. Такое предположение принято называть нулевой гипотезой и обозначать Н₀.

Так, для первой ситуации нулевой гипотезой является допущение того, что сомнительное значение принадлежит к той же генеральной совокупности, что и остальные выборочные данные. Для второй ситуации ею является допущение, что изучаемые явления (объекты) не различаются по средним содержаниям.

Нулевая гипотеза должна быть отвергнута в том случае, если ее вероятность мала На практике она отвергается при Р(Н₀)<, где  —принятый уровень значимости.

В том случае, когда нулевая гипотеза не подтверждается и должна быть отвергнута, различие сравниваемых статистик признается существенным. Если нулевая гипотеза не отверга­ется, утверждать, что рассматриваемые статистики действи­тельно равны, нет оснований, хотя это и возможно. Отбор дополнительных данных может привести к тому, что нулевую гипотезу придется отвергнуть.

Применительно к геологии отмеченное можно пояснить следующим примером. Разбуривается магнитная аномалия. Нулевая гипотеза — рудных скоплений нет. Скважина не встретила рудного тела. Можно ли утверждать, что природа аномалии нерудная? Скважина могла не встретить тела (за­бурена не в том месте, не под тем углом, имеет недостаточ­ную глубину и т. п.). Если скважина подсечет руду, то нуле­вая гипотеза будет отвергнута уверенно!

Принадлежность крайних значении к изучаемой сово­купности. Применение статистических критериев основано на допущении, что распределение изучаемого признака в генеральной совокупности не противоречит определенному за­кону. Для нормально распределенной совокупности аномальность Xi-го значения проверяют с помощью формулы



Если _i > _(n), то x_i (проверяемое) значение является аномальным с вероятностью р=1—а (рис. 1) и должно быть исключено из выборочной совокупности (допустимые значе­ния даются в справочных таблицах).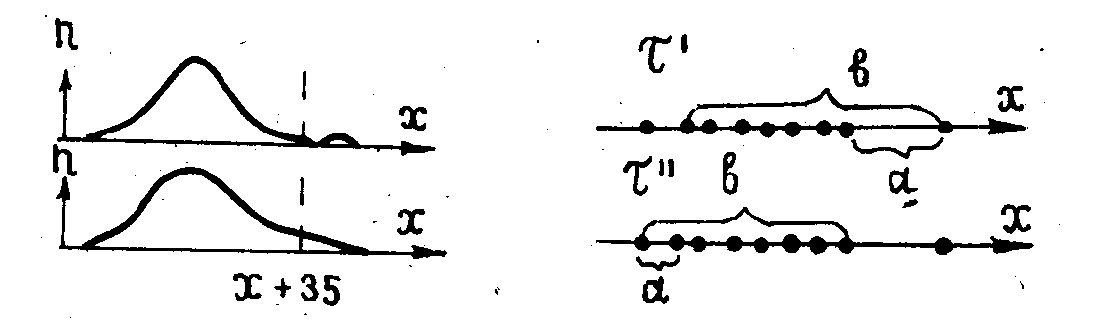

Рис. 1. Примеры графического проявления аномальных значении

Рис. 2. Графический смысл критерия т

Для малых выборок (закон не известен) существует уп­рощенный способ оценки принадлежности крайних значений к заданной совокупности


где  — критерий оценки наибольшего значения,  — наи­меньшего, x₁, x₂, x_n–1, х_n — первое, второе, предпоследнее и последнее значения выборочных данных, упорядоченных по возрастанию. Графическая интерпретация критерия показана на рис. 20. Оценивается отношение разности (а) к разбросу (в). Возможные значения  и  приведены в табличных данных.

Пример. Имеем пять замеров — 1,10; 1,30; 1,35; 1,40; 2,15, по которым необходимо определить среднее значе­ние изучаемого признака. Настороженность вызывает значение 2,15, которое больше предыдущего на 0,75. Оп­ределим = (2,15—1,40) : (2,15—1,30) =0,882. Таблич­ное значение _0,05(5) = 0,689. Так как _эмп > _0,05, то значение 2,15 из подсчета среднего следует исключить.

Сравнение средних значений двух эмпирических совокупностей. Заданы две выборочные совокупности, для которых известны 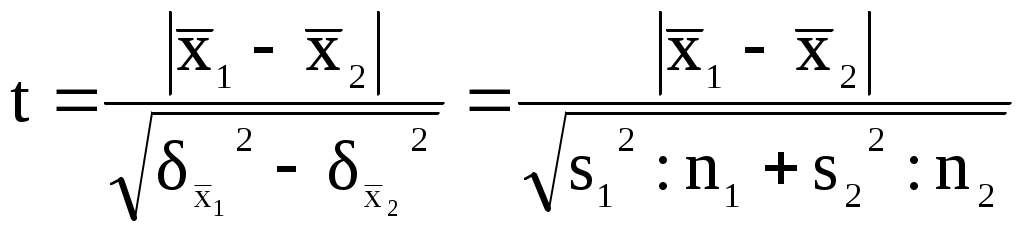, , и или , , n₁, n₂, S₁² и S₂². Нулевая гипотеза состоит в том, что средние существенно не различа­ются. Проверку ее осуществляют с помощью критерия Стьюдента.



второе выражение получено из первого с учетом того, что .

Нулевая гипотеза отвергается, если полученное значение превысит табличное при принятом уровне-значимости а и имеющемся числе степеней свободы f = n₁ + n₂ – 2 (под числом степеней свободы понимают число данных изучаемой совокупности, могущих принимать произ­вольные значения, не изменяющие общего уровня, около ко­торого это варьирование происходит). Допустим, имеем три значения 1, 2, 3, среднее их 2, если попытаться подобрать новую совокупность из трех членов, для которой среднее ра­внялось бы двум, то очевидно, что f=2 — при двух случай­ных, третье должно обеспечить сумму 6, в критерии (4.6) ис­пользуются средние и дисперсии, то есть наложено две связи.

Пример. Для элемента А имеем: =40,15; =0,91; n₁=32; =42,20; =0,85; n₂=40, а элемента В: =1,20; =0,05; =1,00; =0,05. Оценить различие средних. Имеем: =1,65; t_эмп=l,650,05(70)=1,98, то есть различие не­существенное; ; t_эмп=3,0>t_0,05(70)=1,98, то есть различие существенное.

Почему же различие средних в 2,05% для элемента А несущественно, а 0,2 для элемента В — существенно? С вероятностью 0,95 средние по выборкам для элемента А могут иметь значения 40,15±20,91, то есть 38,33–43,06 и 42,2±20,85=40,5–43,9 (большое перекрытие); для элемен­та В имеем 1,2±20,05(1,1–1,3) и 1,0±20,05(0,9–1,1) перекрытия нет (рис. 3).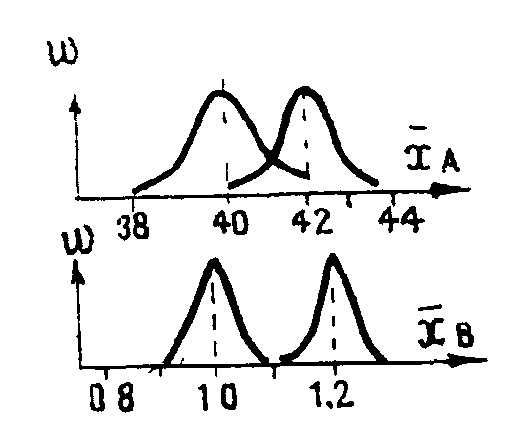



Рис. 3. Графическое представ ление различий

средних содер­жаний элементов А и В
Иногда возникает необходимость определить, существен­но ли отличается выборочное среднее от заданной величины, допустим, сравнить среднее значение разведываемого ком­понента по блоку с минимально-промышленным. Имеем — заданную величину минимально-промышленного содер­жания по блоку, — среднее содержание разведываемого компонента по блоку, — ошибку определения этого среднего. Формула для вычисления критерия Стьюдента при­мет вид



(заданная величина ошибки не имеет, ). Нуле­вая гипотеза не отвергается, если вычисленное значение ока­жется меньше допустимого при принятом уровне значимости и имеющемся числе степеней свободы.

Сравнение совокупностей с попарно связанными замера­ми. В практике геологических работ часто возникает необ­ходимость вести обработку совокупностей с попарно связан­ными замерами (результаты основных и контрольных ана­лизов, данные различных видов опробования одних и тех же забоев и т. п.). Задача состоит в установлении существенно­сти различия таких данных. Для решения ее рассматривают разности каждой пары связанных замеров х_i1—x_i2=_i. Если систематической ошибки нет, то отклонения в большую и меньшую сторону одного замера по отношению к другому должны быть примерно одинаковы, и _i 0.

Совокупность разностей замеров можно рассматривать как некоторый ряд, характеризующийся определенным сред­ним значением 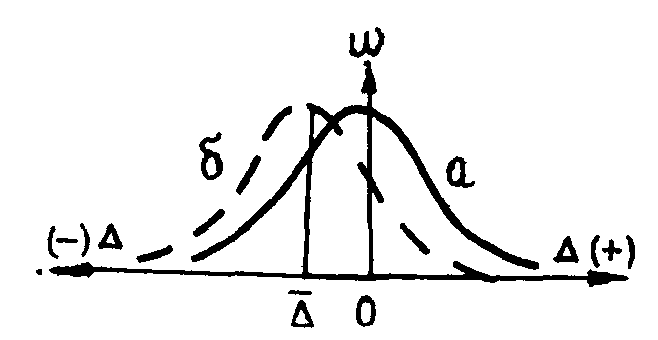и дисперсией S²(). Нулевая гипотеза сос­тоит в том, что =0 (рис. 4).


Рис. 4. Оцениваемое расхож­дение (Д—0) между теорети­ческим (а)

и эмпирическим (б) распределениями критерия раз­ностного ряда