Математические методы в геологии. Контрольная работа по математическим методам в геологии
 Скачать 301 Kb.
|
Критерием проверки нулевой гипотезы является величина ,где  — ошибка среднего. Если полученное значение t не превышает табличного при принятом уровне значимости и данном числе степеней свободы f=n–1, то оснований отвергнуть нулевую гипотезу нет.Сравнение многомерных средних. Сопоставление выборочных совокупностей, охарактеризованных m признаками, может быть осуществимо с помощью критерия Бондаренко [2.3]: 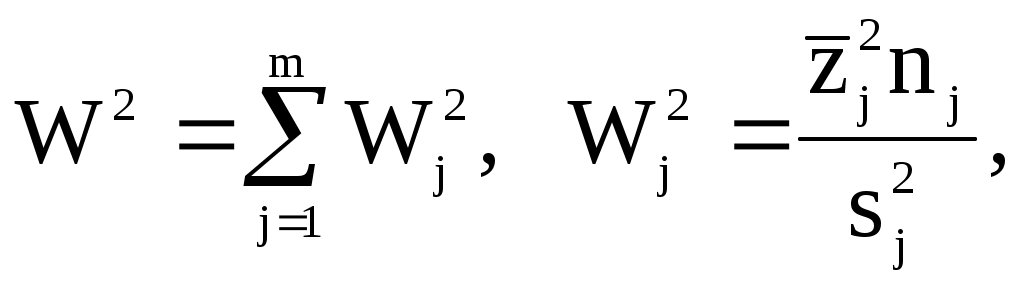 где  — среднее значение разностного ряда j-ro признака, соотнесенного к одному из признаков, являющегося главным; sj — среднее квадратическое отклонение этих значений; nj — число данных j-гo признака. Если Wэмп2>2 (m), то выборки различаются существенно по совокупности признаков. Если Wj2>2 (m=1), то выборки различаются по j-му признаку.Пример. В табл. 1 приведены содержания элемента А в породах при определенных содержаниях кремнекис-лоты. Таблица 1
Оценить, различаются ли породы по содержанию элемента А? Если сравнить содержания элемента А на основе критерия Стьюдента, то получим  =3,00, Sl2=0,55,  =2,1, S22=0,39, tэмп=2,6>t0,05(13)=2,16, следовательно породы существенно различаются по средним значениям.В то же время массив 1 представляет собой более кислые разности пород. При использовании критерия W сравнение содержании элемента А ведут для пород одного ряда кислотности, то есть сопоставляют пробы с одинаковыми содержаниями кремнекислоты. Для данных табл. 1 имеем:
WA.эмп< 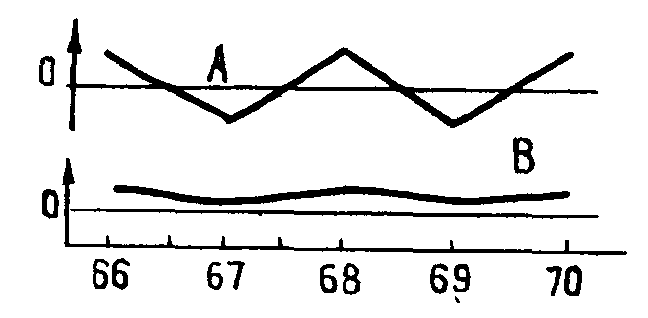 =3,84, говорить о существовании различия пород по содержанию элемента А нет оснований. На рис. 5 показаны расхождения элемента А при различных значениях кремнекислоты. Имеем то плюсовые, то минусовые расхождения, которые могли быть обусловлены ошибками анализа. Допустит, имели бы данные о расхождениях элемента В: 0,2; 0,1; 0,2; 0,2 (сумма 0,7, а квадратов 0,11).  =0,7:5=0,14; s2(z)=0,11:5–0,142=0,0024; WB=(0,1425) : 0,0024=41, что значительно больше допустимого, равного 3,84. Нулевая гипотеза об отсутствии различия пород по этому элементу отвергается (различия небольшие, но закономерные). Рис. 5. Графический смысл различия содержаний при использовании критерия W2 Сравнение дисперсий двух выборочных совокупностей. Нередко выборочные совокупности не различаются по средним, но могут существенно различаться по дисперсиям. Для сравнения дисперсий, используется критерий Фишера:  .Значения критерия Фишера для уровня значимости 0,05 приведены в справочных данных. Таблица имеет два входа по числу степеней свободы: f1=n1–1, f2=n2–1, где n1 — количество проб в выборке, имеющей большую дисперсию. Пример. Оценить различие рассеяния содержаний элемента А в породах двух изучаемых массивов по следующим данным: n1=30, =0,25; s12=0,12; n2=40; =0,25; s22=0,04. Имеем: F=0,12:0,4=3,00. Табличное значение F0,05(29,39) =1,74. Так как Fэмп больше табличного, то различие дисперсий следует признать значимым. Первый массив имеет больший разброс содержаний вокруг среднего, и его следует рассматривать более перспективным на выявление участков, обогащенных элементом А.Сравнение дисперсий имеет большое значение при установлении однородности изучаемого материала. Средние размеры песчинок (гальки, щебня) в пределах сравниваемых участков могут быть одинаковы, а разбросы их вокруг средних — нет. В итоге качество сырья в пределах сравниваемых участков может оказаться различным. Для одновременного сравнения нескольких дисперсий можно воспользоваться критерием Бартлета. Величина 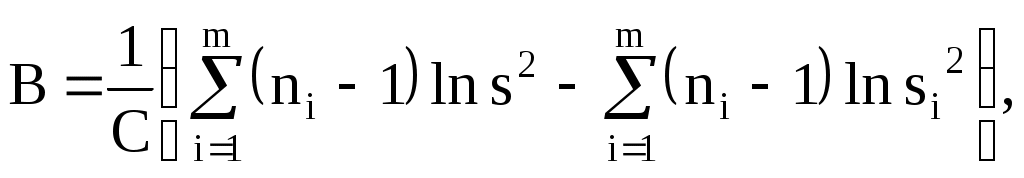 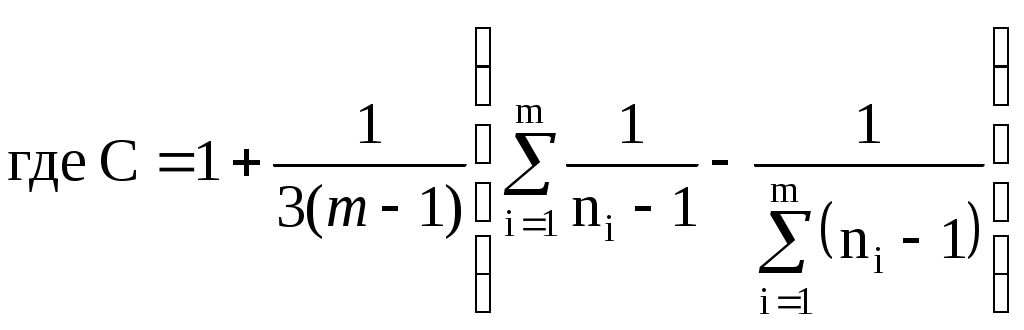 ; ,распределенная как 2 с (  –1) степенями свободы. Если В<2 (m–1), говорить о существенном различии дисперсии нет основания.Сравнение выборочного распределения с теоретическим. После вычисления частот выбранного теоретического распределения необходимо оценить степень согласия между эмпирическими и теоретическими частотами. Для оценки используют критерии и 2. Критерий предложен А. Н. Колмогоровым и И. В. Смирновым. Единственным условием его применения является достаточная численность выборочных данных (нескольких десятков). Для сравнения эмпирического распределения с теоретическим критерий определяют по формуле =D:. где D = |Ni–  |max — наибольшее значение абсолютной разности между накопленными значениями частот эмпирического и теоретического распределений. Теоретическое значение λ не зависит от объема выборки и числа степеней свободы, а определяется только выбранным уровнем значимости. Для =0,05; =1,36; =0,01; =1,63.Расчет критерия покажем на примере обработки данных замера плотности руд одного из рудопроявлений (табл. 2, здесь ni — эмпирические частоты, ñi — теоретические, вычисленные из предположения, что распределение значений плотности не противоречит нормальному закону). Наибольшее значение D=2,0; =2:=29. Так как эмп<0,05, то считать, что эмпирические частоты отличаются от теоретических существенно, нет оснований. Таблица 2
Критерий χ2 предложенный Пирсоном, определяют по формуле χ2=Σ(n1-ñl)2: ñl, где n1 — эмпирическая частота; ñl — теоретическая частота. Если χ2 χ2эмп< χ2α (f), гипотеза о согласии эмпирического и теоретического распределения не отвергается. Число степеней свободы определяется в зависимости от применяемого теоретического закона. Для нормального закона f=k-3 (k—число классов группировки), для закона Пуассона f=k-2. Для применения критерия необходимо, чтобы количество данных в каждом классе было не менее трех—пяти. Расчет критерия покажем на примере обработки предыдущих данных, предварительно объединив классы с малой численностью проб (табл.3). Таблица 3
Число степеней свободы f==5—3==2. Табличное значение χ20,05 (2) =5,99, и отвергать нулевую гипотезу нет оснований, эмпирическое распределение может отвечать нормальному. Графическая интерпретация существа критериев λ, и χ2 показана на рис. 6 (пунктирная линия — эмпирическое, сплошная — теоретическое распределение). В первом случае частоты суммируют и сравнивают наибольшее различие накопленных, во втором — сравнивают сумму относительного различия частот (квадраты — для учета плюсовых и минусовых расхождений). 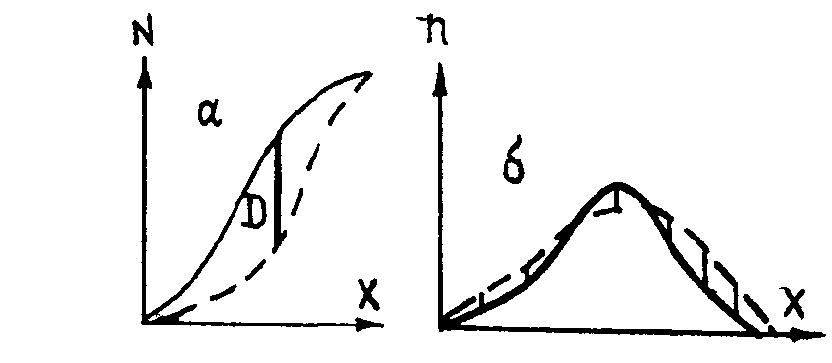 Рис. 6. Графическая интерпретация существа критериев (сравниваемых характеристик распределений) λ (а) и χ2(б) Сравнение двух эмпирических распределений осуществляют с помощью тех же критериев λ и χ2. В этом случае рассматривается различие выборок не по какому-либо из параметров (среднему, дисперсии), а по различию выборочных распределений в целом. Если окажется, что выборочные совокупности распределены одинаково (без уточнения закона такого распределения), то имеющиеся выборки можно рассматривать как принадлежащие к одной генеральной совокупности. Такая проверка особенно важна при объединении данных различных авторов. Для сравнения двух выборочных совокупностей критерий λ, вычисляют по формуле г  де n1, n2—объемы выборок; Ni1, Ni2 - соответствующие накопленные частоты. Расчет критерия показан на примере сравнения двух типов пород по распределению изучаемого признака (табл.4). Таблица 4
М  аксимальное значение разностей равно 0,327, Так как λэмп>λ0,05, то можно считать, что выборочные совокупности различаются по изучаемому признаку. П  ри сравнении двух выборочных совокупностей критерий χ2 вычисляется по формуле: где n1и n2— количество данных в сравниваемых выборках; k — число классов группировки; ni1,ni2 — количество данных в i-том классе первой и второй выборок. Полученное значение χ2 сравнивают с табличным при принятом уровне значимости и числе степеней свободы, равном f—1. Если вычисленное значение больше табличного, то гипотеза о принадлежности выборок к одной генеральной совокупности отвергается. Пример расчета критерия показан в табл. 5. Таблица 5
Полученное значение χ2 == 40664 : (55 х 60) =12,32. Табличное значение χ200,5 (4) =9,49. Так как χ2эмп > χ20.65, то выборочные данные не принадлежат к одной генеральной совокупности. Из непараметрических приведем критерии сравнения выборок по средним значениям, сопоставления сопряженных данных Вилкоксона и сопоставления выборок по распределениям λ' Колмогорова—Смирнова, которые применимы при малом числе данных. Вместо сравнения самих значений x1, x2, ..., xk и y1, у2,…, ym сопоставляют их ранги (номера в упорядоченной единой совокупности) с получением сумм Тх и Ту. Допустимые значения Тα даны таблице «Критические значения критерия Вилкоксона Тα». Если меньшая сумма меньше допустимого, то нулевая гипотеза об отсутствии различия сравниваемых выборок по средним отвергается. При сопоставлении сопряженных данных ранжируются абсолютные расхождения (одинаковым приписывается среднее значение). Определяют сумму рангов менее встречающихся (плюсов или минусов). Сравнивают с допустимым значением. Если она меньше допустимого — различие сравниваемых выборок по значению изучаемого признака существенно. |
,