Контрольная работа за курс 8 класса в формате огэ спецификация и текст итоговой работы. Назначение тестовой работы
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 8 КЛАССА В ФОРМАТЕ ОГЭ Спецификация и текст итоговой работы. Назначение тестовой работы Назначение итоговой работы – выявить и оценить степень соответствия подготовки учащихся 8 классов образовательных учреждений требованиям государственного образовательного стандарта основного общего образования по математике. Нормативно-правовая база Документы, определяющие нормативно-правовую базу аттестационной работы: Федеральный компонент государственного стандарта общего образования (приказ Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования» от 5 марта 2004 года № 1089), Закон Российской Федерации «Об образовании». Характеристика структуры и содержания работы Общее количество заданий в работе – 22 Характеристика структуры работы Всего в работе 22 задания, из которых 18 заданий базового уровня (часть 1), 4 задания повышенного уровня. Работа состоит из двух модулей «Алгебра» и «Геометрия». Модуль «Алгебра» содержит 14 заданий: в части 1 – двенадцать заданий, в части 2 – два задания. Модуль «Геометрия» содержит 8 заданий: в части 1 – шесть заданий, в части 2 – два задания. Часть 1 предусматривает две формы ответа: с выбором ответа из четырех предложенных, с кратким ответом. В части 2 нужно оформить развернутый ответ с записью решения. Распределение заданий по частям работы
Итоговая работа по математике в 8 классе в форме ОГЭ. Вариант 1 Часть 1
Найдите значение выражения: 2,4 + 0,241,2 Ответ:____________________ Решите уравнение: - 9(8-9х) = 4х + 5 Ответ:____________________ На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу 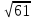 . .К 1) точка A 2) точка B 3) точка C 4) точка D Найдите значение выражения 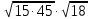 . . 1) 360 2) 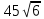 3) 3) 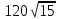 4) 4) 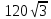 Решите уравнение 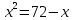 . .Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. Ответ:____________________ Чашка, которая стоила 70 рублей, продаётся с 10%-й скидкой. При покупке 12 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить? Ответ:____________________ В первом ряду кинозала 25 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в 7 ряду? Ответ:____________________ Упростите выражение 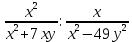 и найдите его значение при и найдите его значение при 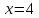 , у = , у = 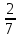 . В ответ запишите полученное число. . В ответ запишите полученное число.Ответ:____________________ В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150 + 11 · (t − 5), где t — длительность поездки, выраженная в минутах (t > 5). Пользуясь этой формулой, рассчитайте стоимость 11-минутной поездки. Ответ:____________________ Решите неравенство . 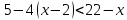 . .1) 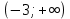 ; 2) ; 2) 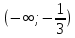 ; 3) ; 3) 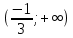 ; 4) ; 4) 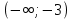 . .
Вычислите: 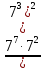 . Ответ: ________________________ . Ответ: ________________________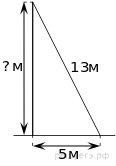
Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах Ответ:____________________ Н 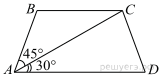 айдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, айдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы,равные 30° и 45° соответственно. Ответ:____________________ 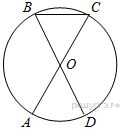 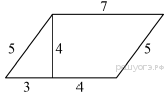 AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах. AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.Ответ:____________________ Найдите площадь параллелограмма, изображённого на рисунке. Ответ:____________________ Н 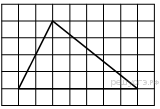 а клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь. а клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.Ответ:____________________ Какие из следующих утверждений верны? 1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат. 2) Сумма смежных углов равна 180°. 3) Любая высота равнобедренного треугольника является его биссектрисой. Если утверждений несколько, запишите их номера в порядке возрастания. Часть 2
Решите уравнение: х4 – 2х2 – 15 = 0 Теплоход проходит по течению реки до пункта назначения 176 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба. 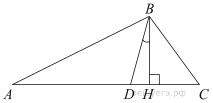 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD. ВАРИАНТ 2 Часть 1
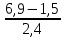 Ответ:____________________ Ответ:____________________2. Решите уравнение: -2(8+7х) = 9х + 4 3. Одна из точек, отмеченных на координатной прямой, соответствует числу 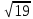 . Какая это точка? . Какая это точка?4. Найдите значение выражения: 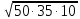 . . 1) 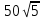 2) 2) 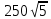 3) 3) 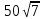 4) 250 4) 2505. Решите уравнение: 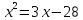 . .Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. Ответ:____________________ 6. Спортивный магазин проводит акцию. Любая футболка стоит 400 рублей. При покупке двух футболок — скидка на вторую 40%. Сколько рублей придётся заплатить за покупку двух футболок? Ответ:____________________ 7. В первом ряду кинозала 19 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в 8 ряду? 8. Упростите выражение 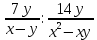 и найдите его значение при и найдите его значение при 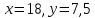 . . Ответ:____________________ 9. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле Ответ:____________________ 1 и определите, на каком рисунке изображено множество его решений. 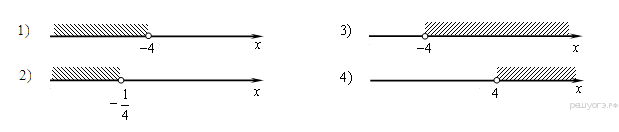 1 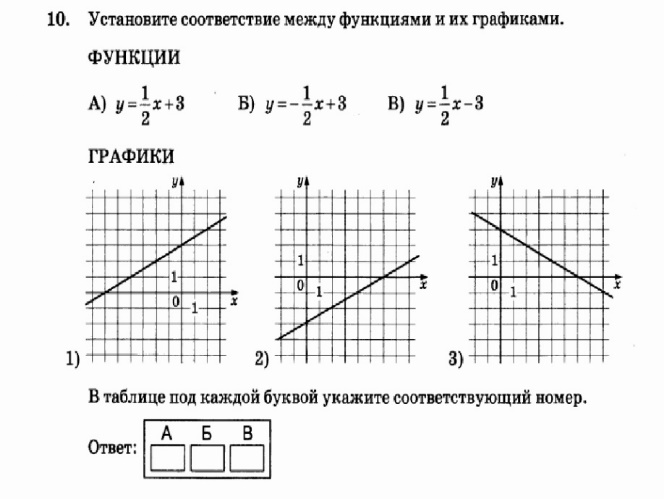 1. 1. 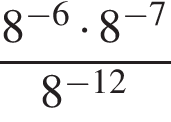 12. Вычислите: 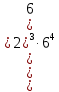 . Ответ: ________________________ . Ответ: ________________________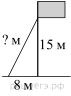
13. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса. 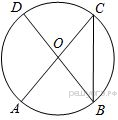 Ответ:____________________ Ответ:____________________14. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона AC равна 37, сторона BC равна 74. Найдите MN. Ответ:____________________ 1 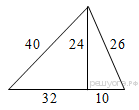 5. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах. 5. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.Ответ:____________________ 16. Найдите площадь треугольника, изображённого на рисунке. 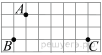 17.На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. 17.На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 18. Какие из данных утверждений верны? Запишите их номера. 1) Каждая из биссектрис равнобедренного треугольника является его медианой. 2) Диагонали прямоугольника равны. 3) Все высоты равностороннего треугольника равны. Часть 2
19. Решите уравнение х4 – 4х2 – 21 = 0 20. Теплоход проходит по течению реки до пункта назначения 140 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 11 часов, а в пункт отправления теплоход возвращается через 32 часа после отплытия из него.
21. Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба. 22. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD. 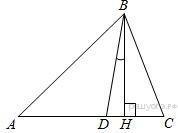 Итоговая работа по математике в 8 классе в форме ОГЭ. Вариант 3 Часть 1
Найдите значение выражения: -5,6 + 1,3 · 0,8. Решите уравнение: - 3· (4 - 6х) = 12х – 33. 3 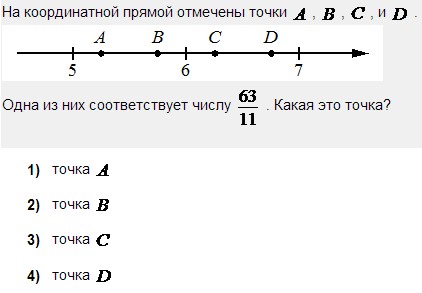 . . 1) точка A 2) точка B 3) точка C 4) точка D Найдите значение выражения 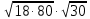 . . 1) 360 2) 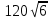 3) 3) 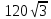 4) 4) 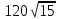 Решите уравнение 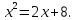 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. Платье стоит 2120 рублей. Скидка в день распродажи равна 35%. Сколько стоит платье в день распродажи? На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей наугад берет один пирожок. Найдите вероятность того, что пирожок окажется с повидлом. Упростите выражение (а – 3)2 – а · (5а -6) и найдите его значение при а = 4. В ответ запишите полученное число. Расстояние S (в метрах) до места удара молнии можно приближённо вычислить по формуле S = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых. Решите неравенство 4х + 5 ≤ 6х – 2 и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.  Установите соответствие между функциями и их графиками. ФУНКЦИИ А) у = - 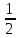 х + 2; Б) у = - х + 2; Б) у = - 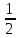 х - 2; В) у = х - 2; В) у = 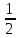 х – 2. х – 2. ГРАФИКИ 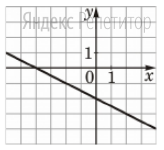
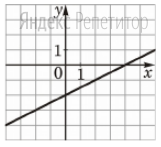 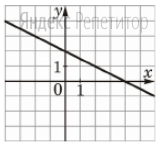 . 2. 3. . 2. 3. Вычислите: 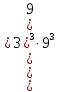 . Ответ: ________________________ . Ответ: ________________________
Биссектрисы углов N и M треугольника MNP пересекаются в точке A. Найдите 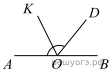 Н  айдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах. айдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах. В равнобедренном треугольнике АВС АС = ВС. Найдите АС , 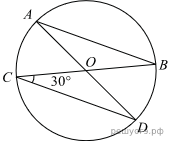 если высота СН = 12, сторона АВ = 10. если высота СН = 12, сторона АВ = 10.В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB. Н 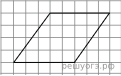 а клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь. а клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь. Какие из следующих утверждений верны? 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. Если утверждений несколько, запишите их номера в порядке возрастания. Часть 2
Решите уравнение: (х + 2)2 = (х - 4)2. Первая труба пропускает на 3 литра воды за минуту меньше, чем вторая труба. Сколько литров воды за минуту пропускает первая труба, если резервуар объемом 260 литров она заполняет на 6 минуты дольше, чем вторая труба?
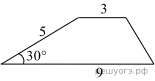 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9. Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.  Итоговая работа по математике в 8 классе в форме ОГЭ. Вариант 4 Часть 1
Найдите значение выражения: -7,8 + 2,4 · 0,9. Решите уравнение: - 6· (3 - 4х) = 18х + 6. 3 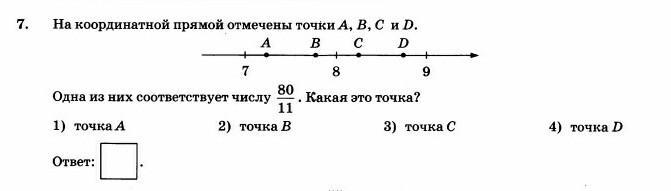 . .Найдите значение выражения  . . 1) 120 2)  3) 3) 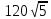 4) 4) 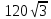 Решите уравнение 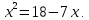 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. В октябре кг апельсинов стоил 56 рублей. В ноябре апельсин подорожали на 15%. Сколько рублей стоил 1 кг апельсинов после подорожания? Решите неравенство . 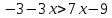 . .1) 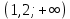 ; 2) ; 2) 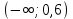 ; 3) ; 3) 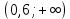 ; 4) ; 4) 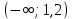 . .8. На тарелке лежат одинаковые на вид пирожки: 7 с мясом, 8 с рисом и 25 с повидлом. Андрей наугад берет один пирожок. Найдите вероятность того, что пирожок окажется с повидлом. Упростите выражение (а + 2)2 – а · (4 – 7а) и найдите его значение при а = 2. В ответ запишите полученное число. Расстояние S (в метрах) до места удара молнии можно приближённо вычислить по формуле S = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 17 с. Ответ дайте в километрах, округлив его до целых. На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b. 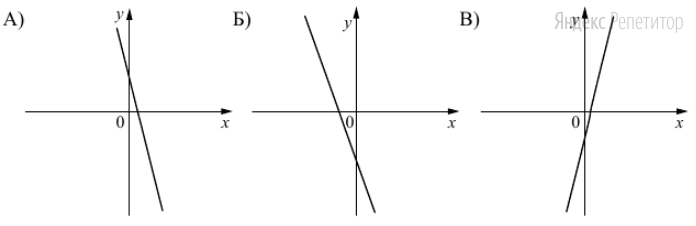 ГРАФИКИ ГРАФИКИКОЭФФИЦИЕНТЫ k < 0, b > 0. k < 0, b < 0. k > 0, b < 0. Вычислите: 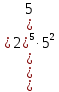 . Ответ: ________________________ . Ответ: ________________________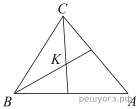
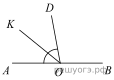 Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.  В равнобедренном треугольнике АВС АС = ВС. Найдите АН , если высота СН = 8, 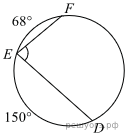 АС = 10. АС = 10. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно. Н 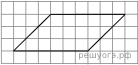 а клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь. а клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.Какие из следующих утверждений верны? 1) Если угол острый, то смежный с ним угол также является острым. 2) Диагонали квадрата взаимно перпендикулярны. 3) Все диаметры окружности равны между собой. Если утверждений несколько, запишите их номера в порядке возрастания. Часть 2
Решите уравнение: (х + 10)2 = (5 – х )2. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 110 литров она заполняет на 1 минуту быстрее, чем первая труба?
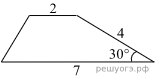 Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30° . Найдите площадь трапеции, если её основания равны 2 и 7.  Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба. Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба. |
