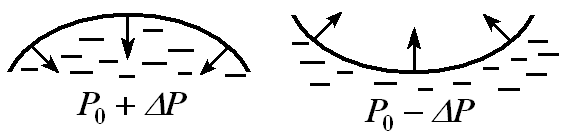Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки

• Название: Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
• Дата: 10.10.2018
• Размер: 1.81 Mb.
• Имя файла: nurik.docx
• Тип: Контрольные вопросы; #53040
• страница: 12 из 22

32. Свойства жидкостей

План

1. 
   Характеристика жидкого состояния. Ближний порядок.
   
2. 
   Поверхностное натяжение. Силы, возникающие на кривой поверхности. Формула Лапласа. Смачивание и капиллярные явления.
   

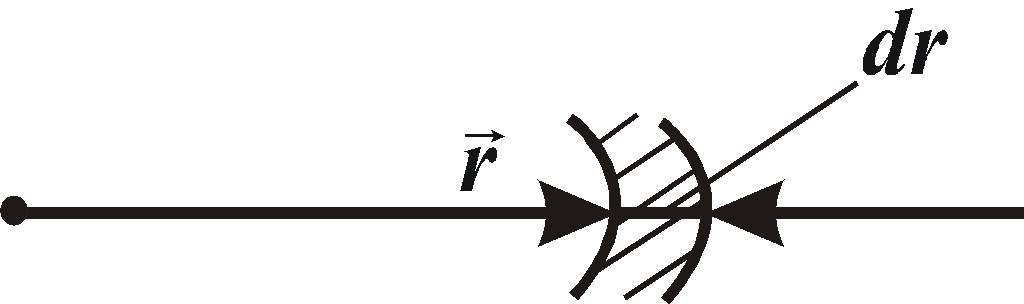
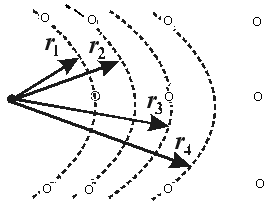
1. Характеристика жидкого состояния.Жидкое состояние, занимает промежуточное положение между газами и кристаллами, сочетает в себе некоторые черты обоих этих состояний. Для кристаллического состояния характерно упорядоченное расположение частиц (атомов или молекул), в газах в этом смысле полный хаос. Согласно рентгенографическим исследованиям, в отношении характера расположения частиц жидкости занимают промежуточное положение.

В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится всё менее упорядоченным и довольно быстро порядок в расположении частиц полностью исчезает.

В кристаллах имеет место дальний порядок – упорядоченное расположения частиц по отношению к любой частице наблюдается в пределах значительного объёма.

Оценить структуру вещества позволяет радиальная функция распределения (в некоторых учебниках она называется парной функцией распределения). Выберем некоторую молекулу в качестве тела отсчёта. Среднее число молекул в сферическом слое объёмом , находящихся на расстоянииr от выбранной молекулы (Рис. 10.1) обозначим dN(r). Вероятность обнаружить молекулы в этом сферическом слое

	, где N – общее число молекул в некотором рассматриваемом объёме V, g(r) – радиальная функция распределения. В
Рис. 10.1

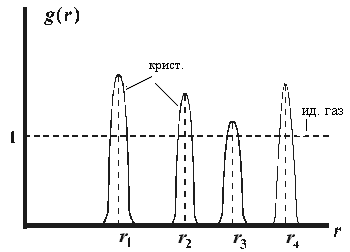
случае идеального газа никакие элементы объёма не имеют преимущества и вероятность нахождения частицы в данном объёме пропорционально объёму и g(r)=1.

В идеальном кристалле структура жёсткая и все взаимные расстояния являются фиксированными (Рис. 10.2).

	Говорят, что в идеальном газе вообще нет порядка, а в кристалле – дальний порядок – на любом расстоянии от данного атома находится строго определённое количество других атомов, располагающихся друг относительно друга строго определённо. Радиальные функции распределения для кристаллов и идеального газа представлены на рис. 10.3.
Рис. 10.2

Пики соответствует узлам решётки, а конечная ширина линии g(r) является следствием колебаний атомов относительно узла в реальном кристалле.

	Заметим, что для кристаллазависит не только от модуля вектора, но и от его направления. В некотором другом направлении пики могут находится на других расстояниях. Для жидкостей функцияпредставлена на рис. 10.4. На малых расстояниях поведение подобно кристаллам (пики чередуются, но
Рис. 10.3

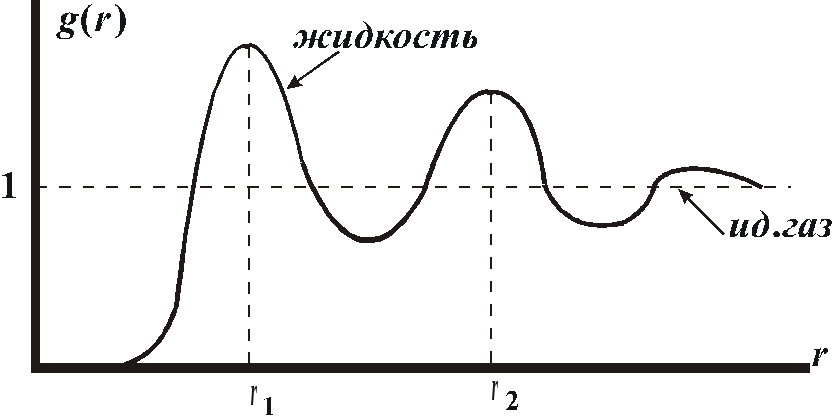
более сглажены, чем у кристалла). На дальних расстояниях кривая стремится к 1 как для идеального газа.

	В жидкостях с удлиненными молекулами наблюдается взаимная ориентация молекул в пределах значительного объёма, чем обуславливается анизотропия оптических и некоторых других свойств. Такие жидкости получили названиежидких кристаллов. У них
Рис. 10.4

упорядочена только ориентация, взаимное же расположение, как и в обычных жидкостях, дальнего порядка не обнаруживает.

2. 
   Поверхностное натяжение.
   

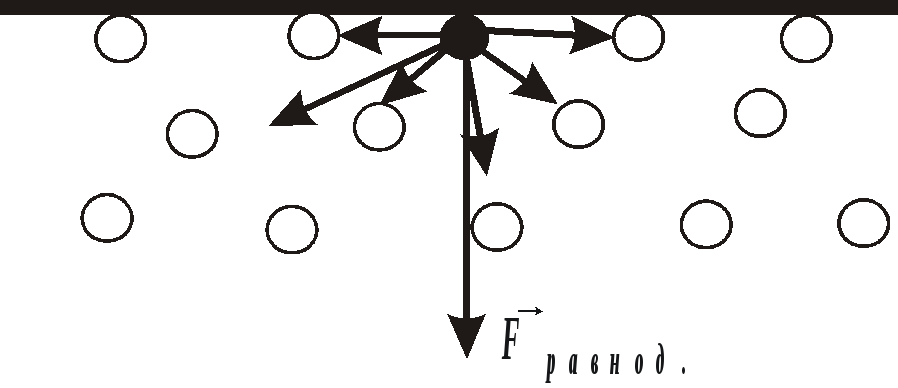
Молекулы жидкости располагаются настолько близко друг к другу, что силы притяжения между ними имеют значительную величину. Взаимодействие быстро убывает с расстоянием, начиная с некоторого расстояния r (радиус молекулярного действия). На каждую молекулу, находящуюся в поверхностном слое толщиной r , будет действовать сила, направленная внутрь жидкости (Рис. 10.5).

	Переход молекулы из глубины жидкости в поверхностный слой связан с необходимостью совершения работы против действующих в поверхностном слое сил. Эта работа (за счёт кинетической энергии молекул) идёт
Рис. 10.5

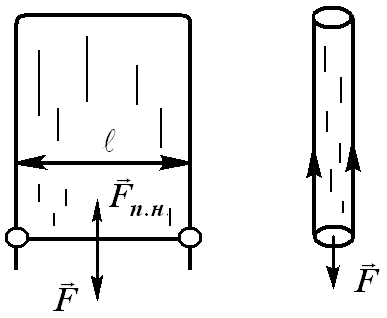
на увеличение потенциальной энергии молекулы. То есть в поверхностном слое молекулы обладают дополнительной потенциальной энергией - поверхностной .

Из-за наличия действующих на молекулы в поверхностном слое сил, направленных внутрь жидкости, жидкость стремится к сокращению своей поверхности, как если бы она была заключена в упруго растянутую плёнку, стремящуюся сжаться (никакой плёнки на самом деле нет).

Представим плёнку жидкости (например, мыльную плёнку), натянутую на проволочную рамку, одна из сторон которой (перемычка) может перемещаться (Рис. 10.6). Благодаря стремлению поверхности уменьшиться, на проволочку будет действовать сила. Она направлена по касательной к поверхности жидкости, перпендикулярно к участку контура (длина перемычки), на который она действует ().

	Сила поверхностного натяжения, приходящаяся на единицу длины участка контура , называетсякоэффициентом поверхностного натяжения (размерность н/м). Вследствие стремления поверхностного слоя к сокращению со стороны плёнки будет действовать на перемычку сила, равная . Чтобы перемычка находилась в равновесии, к ней нужно приложить внешнюю силуF,
Рис. 10.6

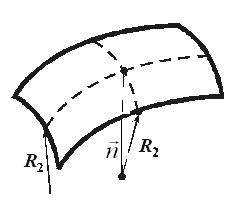
равную силе натяжения плёнки, т.е. . Коэффициент 2 появляется из-за того, что плёнка имеет два поверхностных слоя.

Жидкость вне поля внешних сил будет принимать форму с минимальной поверхностью, т.е. форму шара.

Давление под искривлённой поверхностью.

В случае искривлённой поверхности силы поверхностного натяжения стремятся сократить эту поверхность. (Рис. 10.7).

	Благодаря этим силам в жидкости возникает дополнительное давление, а давление в жидкости, где-
Рис. 10.7

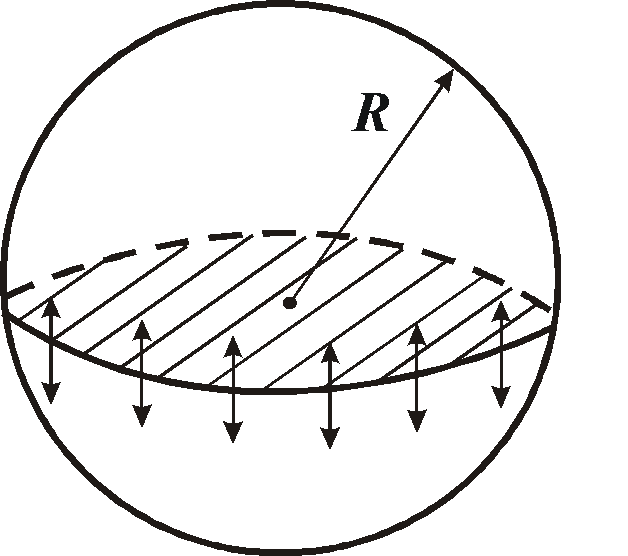
давление в случае неискривлённой поверхности, причём >0 в случае выпуклой поверхности, и<0, если поверхность вогнутая (в этом случае поверхностный слой, стремится сократиться, растягивает жидкость и давление уменьшается).

Вычислим дополнительное давление для сферической поверхности жидкости. Рассечём мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария. Из-за поверхностного натяжения

		оба полушария (Рис. 10.8) притягиваются друг к другу с силой: . Эта сила прижимает друг к другу оба полушария по поверхности и обуславливает дополнительное давление: Лаплас обобщил эту формулу на поверхность любой формы.
Рис. 10.8

Формула Лапласа выглядит так:

		Где и– радиусы кривизны в двух взаимно перпендикулярных плоскостях, пересечение которых совпадает с нормалью к поверхности жидкости в интересующей нас точке (Рис. 10.9). Например, для поверхности цилиндрической формы один из радиусов кривизны стремится ки .
Рис. 10.9

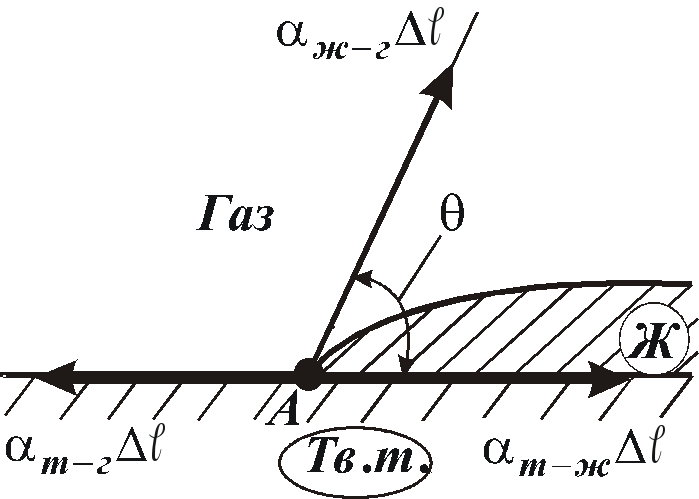
Смачивание и капиллярные явления.

Смачивание – явление, возникающее при соприкосновении жидкости с поверхностью твёрдого тела или другой жидкости. Выражается, в частности, в растекании жидкости по твёрдой поверхности. Смачивание вызывает образование мениска в капиллярной трубке, определяет форму капли на твёрдой поверхности и др. (Заметим, что обычно смачивание рассматривают как результат межмолекурного взаимодействия, однако смачивание может быть результатом химической реакции, диффузионных процессов).

Мерой смачивания обычно служит краевой угол между касательными к поверхности жидкости. (Рис. 10.10). Если , то говорят, что

	жидкость смачиваетповерхность твёрдого тела. При имеет местополное смачивание. Если , то жидкостьне смачивает поверхность. При мы имеемполное несмачивание. Условие равновесия элемента контура длиной (расположен перпендикулярно плоскости рисунка 10.10 в т. А).
Рис. 10.10

,

где коэффициенты поверхностного натяжения жидкости на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. Сокращая на, получимдля краевого угла соотношение:

(Например, полное смачивание будет при ).

Смачивание имеет важное значение в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, пайке. Примеси сильно сказываются на величине поверхностного натяжения. Например, растворение в воде мыла уменьшает её коэффициент поверхностного натяжения почти в 1,5 раза (что, в частности и обуславливает использование мыла в качестве моющего средства). Несмачивание может приводить к тому, что из решета, нити которого покрыты парафином (при небольшом уровне воды), вода не выливается, опровергая известную поговорку.