Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
 Скачать 1.81 Mb.
|
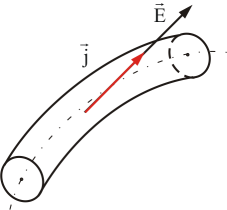
42. Поляризация диэлектриков. Вектор поляризации.Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.
Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема. Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры. Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле c напряжённостью  , направленное против внешнего поля с напряжённостью  . В результате напряжённость поля  внутри диэлектрика будет выражаться равенством: 31 Связь вектора поляризации и поверхностной плотности связанных (поляризационных) зарядов 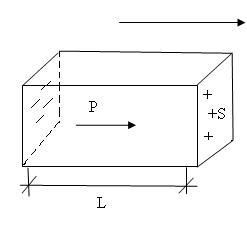  Рассмотрим диэлектрик во внешнем электрическом поле напряженностью . Пусть S - площадь поляризованной поверхности. Поляризованный однородный диэлектрик можно рассматривать как макроскопический диполь, электрический момент которого:  Вектор поляризации диэлектрика - это электрический момент единицы объёма, т. е. 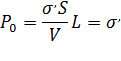 Следовательно:  Если вектор составляет с нормалью к поверхности S диэлектрика угол α (Рис.), то поверхностная плотность связанных зарядов σ’ равна нормальной составляющей вектора поляризации:  Поляризуемость численно равна величине поляризационных зарядов на единицу площади, перпендикулярной вектору поляризации. 32 Теорема Гаусса о потоке электрической индукции.Мы будем доказывать эту теорему, исходя из закона обратных квадратов и предполагая, что все пространство заполнено однородным диэлектриком. Последнее предположение будет в дальнейшем снято. Рассмотрим малый элемент замкнутой поверхности (фиг. 6), внешняя нормаль к которой образует угол а с радиус-вектором из точки в которой расположен точечный заряд Каждую точку границы элемента соединим прямой линией с точкой так чтобы образовался малый конус. Этот конус имеет сечение со сферической поверхностью, проходящей через точку и имеющей центр в точке поэтому сова. Нормальная составляющая напряженности поля, созданного в точке зарядом находящимся в точке равна  Нормальная компонента потока сквозь площадку определяется, как  Телесный угол, под которым видна площадка из точки равен так что  Если точка находится внутри замкнутой поверхности, то конус пересекает поверхность раз, причем и — число нечетное; угол а оказывается раз острым и раз тупым, так что суммарная величина потока в конусе равна Фиг. 6. Если же точка находится вне поверхности, то — число четное, и количество отрицательных и положительных значений одинаково; поэтому их суммарный вклад равен нулю. Чтобы получить полный поток сквозь поверхность, окружающую заряд, нужно проинтегрировать по ней нормальную компоненту что дает 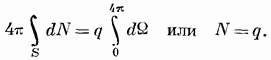 Добавляя сюда ноток, обусловленный всеми зарядами, находящимися внутри мы получаем теорему Гаусса, гласящую, что если на произвольной замкнутой поверхности задана напряженность электрического ноля то  где единичный вектор внешней нормали к поверхности, а интегрирование производится всей поверхности, охватывающей заряд Если пространство вне рассматриваемой поверхности является неоднородным и содержит различные диэлектрические и проводящие тела, то необходимо ввести определенные предположения относительно электрических свойств веществ в электростатических полях. Поэтому при рассмотрении таких полей мы будем считать, что природа всех тел чисто электрическая и что они состоят из положительных иотрицательных зарядов, ноля которых подчиняются закону обратных квадратов. гипотеза позволяет объяснить электростатические явления в любом материальном теле путем сложения полей всех составляющих его зарядов. Следовательно, уравнение (1.27) остается в силе независимо от нриридьг диэлектрических или проводящих веществ, находящихся вне рассматриваемой поверхности, так как оно учитывает поля, созданные внешними зарядами. Принятая нами гипотеза содержится в явном или неявном виде в большинстве курсов по электростатике. 43. http://fb.ru/article/333399/dielektricheskaya-vospriimchivost-i-dielektricheskaya-pronitsaemost 44.
45. | |||||||||||||||||||||
