Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
 Скачать 1.81 Mb.
|
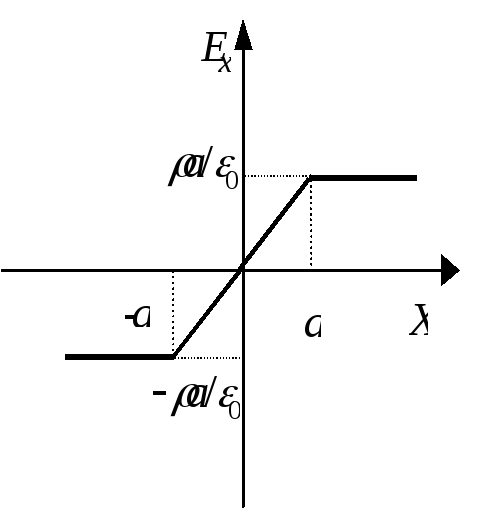
37. Электрическое поле заряженной пластиныПример 2.9. Область пространства, ограниченная двумя параллельными друг другу бесконечными плоскостями, расположенными на расстоянии 2а друг от друга, заряжена однородно по объему с плотностью . Используя формулировку электростатической теоремы Гаусса, покажите, что 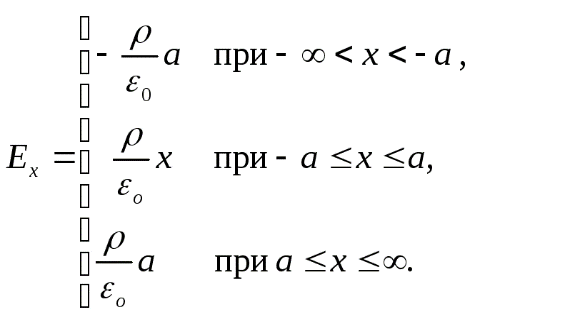 Ось Х перпендикулярна упомянутым бесконечным плоскостям, а точка х = 0 выбрана в центре слоя. Зависимость Ex(x) представьте графически. Решение. В силу симметрии распределения заряда, линии напряженности перпендикулярны рассматриваемому слою и направлены от центральной плоскости слоя в обе стороны. Поэтому в качестве замкнутой гауссовой поверхности построим цилиндр, основания которого параллельны и симметричны плоскости, соответствующей положению x=0 заряженного слоя, а ось перпендикулярна ему. Согласно теореме Гаусса:  .Так как образующие цилиндра параллельны линиям напряженности  , то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю. А полный поток через гауссову поверхность равен сумме потоков через его основания, то есть равен .Используя теорему Гаусса, найдем напряженность электрического поля вне и внутри заряженного слоя. При  заряд, заключенный внутри цилиндрической поверхности, равен , поэтому напряженность электрического поля внутри слоя равна .При  заряд, заключенный внутри цилиндрической поверхности, равен , поэтому напряженность электрического поля снаружи слоя равна .График напряженности проекции  показан на Рис.8.
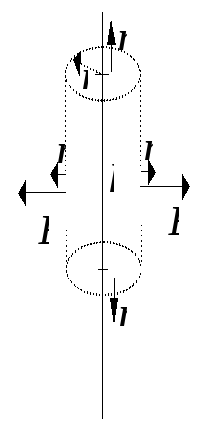
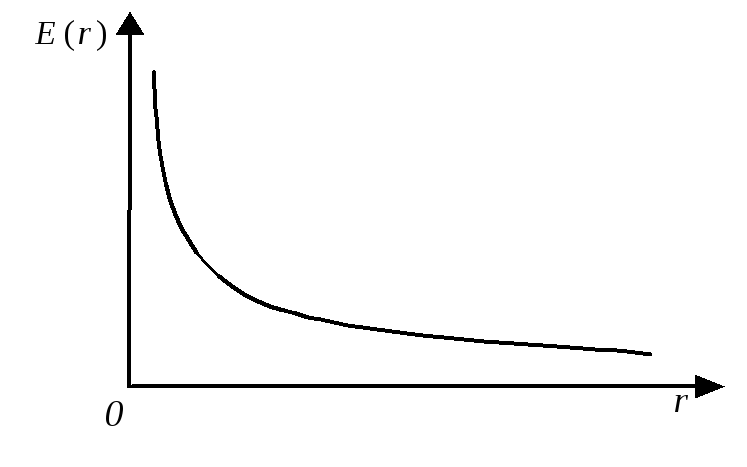
Электрическое поле заряженной нитиПример 2.10. Вычислить напряженность электрического поля бесконечно тонкой и бесконечно длинной прямолинейной нити, однородно заряженной электричеством с линейной плотностью l. Решение. Найдем напряженность электрического поляс помощью теоремы Гаусса. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что векторнаправлен радиально к линии заряда или от нее, в зависимости от знака заряда. Ввиду той же симметрии величинаЕможет зависеть только от расстояния до заряженной нити Е =Е( r ). Для определения этой зависимости выберем гауссову поверхность следующим образом. Построим цилиндр с боковой поверхностью удаленной от нити на расстояние rи основаниями, перпендикулярными к нити (Рис.9а). Поток векторачерез оба основания цилиндра равен нулю, т.к.  . Поток через боковую поверхность равенЕ× S, т.к. ,S- площадь боковой поверхности. Поэтому полный поток через выбранную Гауссову поверхность равен .Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:  Применяя теорему Гаусса, получим соотношение:  ,откуда найдем  .График зависимости представлен на Рис.9б.
|
