Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки

• Название: Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
• Дата: 10.10.2018
• Размер: 1.81 Mb.
• Имя файла: nurik.docx
• Тип: Контрольные вопросы; #53040
• страница: 18 из 22

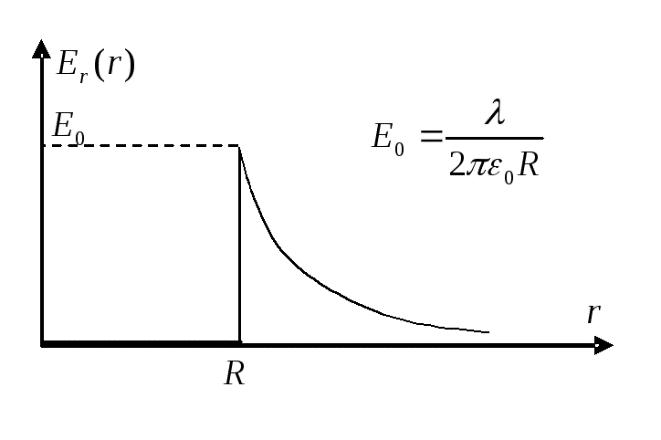
Электрическое поле заряженного цилиндра

Пример 2.11.

Поверхность бесконечного длинного кругового цилиндра заряжена однородно с линейной плотностью λ. Определите напряженность электрического поля внутри и вне цилиндра. Полученный результат представьте на графике, где- проекция вектора напряженности на осьr, перпендикулярную поверхности цилиндра, с началом отсчета на его оси симметрии.

Решение.

Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор направлен радиально - к линии оси цилиндра или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина напряженности может зависеть только от расстояния до оси цилиндра:

Е = Е ( r ).

Для определения этой зависимости выберем гауссову поверхность следующим образом. Построим цилиндр с боковой поверхностью удаленной от оси на расстояние и основаниями, перпендикулярными к оси цилиндра. Поток векторачерез оба основания цилиндра равен нулю, т.к.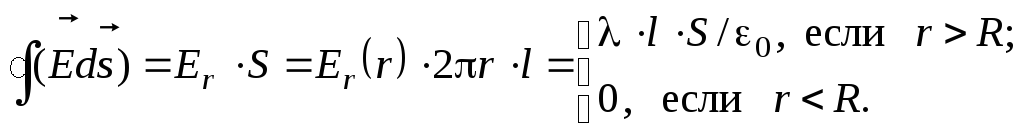. Поток через боковую поверхность равенЕ× S, т.к., S- площадь боковой поверхности. Из теоремы Гаусса следует:



Для величины проекции получим:

, еслиr

, если>R.

График этой зависимости, представленный на Рис.10, характеризуется скачком величины напряженности при , что отражает идеализацию распределения заряда на геометрической поверхности.

Рис.10

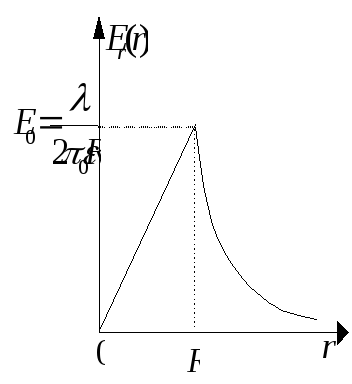
Пример 2.12.

Область внутри бесконечного длинного кругового прямого цилиндра радиуса Rзаряжена однородно с объемной плотностьюρ. Определите напряженность электрического поля внутри и вне цилиндра. Полученный результат представьте на графике, где- проекция вектора напряженности на осьr, перпендикулярную поверхности цилиндра, с началом отсчета на его оси симметрии.

Решение.

Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор направлен радиально - к линии оси распределения заряда или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина Е может зависеть только от расстояния до оси:

Е = Е ( r )

Для определения этой зависимости выберем гауссову поверхность следующим образом . Построим цилиндр с боковой поверхностью удаленной от нити на расстояние r и основаниями, перпендикулярными к нити. Высота цилиндра. Поток векторачерез оба основания цилиндра равен нулю, т.к.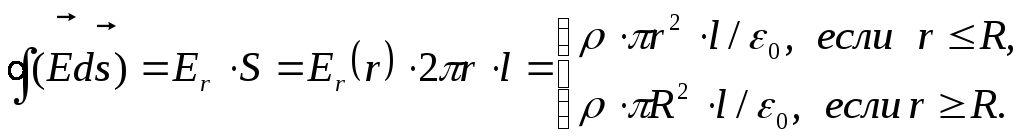. Поток через боковую поверхность равенЕ× S, т.к., S- площадь боковой поверхности. Из теоремы Гаусса следует:



Для величины проекции получим:

при

при.

График, представленный на Рис.11 характеризуется отсутствием скачка величины напряженности поля при r=Rв отличие от случая распределения заряда на поверхности цилиндра.

Рис.11

Дифференциальная форма теоремы Гаусса Пример 2.13 В некоторой области вектор напряженности электрического поля зависит от координат x, y, z прямоугольной системы координат по закону, где - известная постоянная, ,и- орты осей. Определите объемную плотность заряда в данной области. Решение. Плотность распределения заряда определяется выражением. Представляя дивергенцию в координатной форме, получим:

Пример 2.14

Вычислите дивергенцию напряженности электрического поля точечного заряда в произвольной точке пространства в декартовой системе координат.

Решение.

Локальная форма теоремы Гаусса позволяет выразить дивергенцию напряженности электрического поля через локальную плотность распределения заряда по соотношению . Плотность объемного распределения точечного заряда равна нулю в любой точке вне заряда. Следовательно,, при. Конечно же, этот результат можно получить и прямым расчетом:



так как=,=,=