Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
 Скачать 1.81 Mb.
|
38. Работа по перемещению заряда в электрическом поле. Потен циалТеперь известно, что на заряд, помещенный в электрическое поле, действует сила. Следовательно, перемещение заряда в элек трическом поле будет сопровождаться работой dA = Fdl dA > 0 в случае, если работа совершается силами поля; dA < 0 в случае, если работа совершается внешними силами против сил поля. Рассмотрим перемещение пробного заряда Q0 из точки 1 в точку 2 в поле сил, создаваемых зарядом Q. Поле сил – центральное (рис. 73). Работа на пути dl будет равна  Отсюда работа по перемещению заряда из точки 1 в точку 2  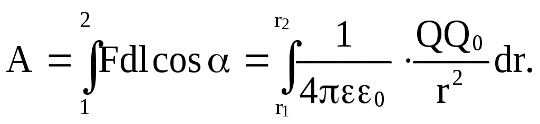 Если работа совершается внешними силами, то  Электростатическое поле является потенциальным. Это значит, что работа по перемещению заряда не зависит от пути, по которому перемещается заряд, а зависит только от начального и конечного положения заряда. Тело, находящееся в потенциальном поле сил, обладает по тенциальной энергией, за счет которой совершается работа силами поля. Следовательно, полученное выражение для работы можно представить как разность потенциальных энергий заряда Q0 в поле сил, созданном зарядом Q  Таким образом, потенциальная энергия в каждой точке поля зависит от величины пробного заряда Q0. Но если взять отношение W/Q0, то оно будет зависеть только от точки поля, и не будет зависеть от величины помещенного в эту точку за ряда. Отношение  = φ называют потенциалом поля.Потенциалом электрического поля называется физическая величина, равная отношению потенциальной энергии, которую приобретает положи тельный заряд Q0, если его переместить из  в данную точку поля, к величине этого заряда .Из равенства А12 = -А21 следует другое определение. Потенциалом поля называется физическая величина, чис ленно равная работе, которую совершают силы поля над единичным положительным зарядом, при удалении его из данной точки поля в бесконечность. Потенциал – величина скалярная. При суперпозиции (нало жении) электрических полей потенциал суммарного электрического поля определяется как алгебраическая сумма потенциалов налагае мых полей  Выражение для работы по перемещению заряда из точки с потен циалом φ1в точку с потенциалом φ2 имеет вид A12 = Q (φ2 – φ1). Работа измеряется в Дж или эВ. 1эВ = 1,6 ∙10-19 Дж. Для наглядного изображения поля вместо линий напряжен ности (силовых линий) можно воспользоваться поверхностями рав ного потенциала или эквипотенциальными поверхностями. Экви потенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция координат x, y, z, то уравнение эквипотенциальной поверхности имеет вид: φ (x,y,z) = const. Эквипотенциальные линии – линии, образующиеся от пересечения эквипотенциальной поверхности плоскостью проводятся так, что направление нормали к ним совпадает с направлением вектора в той же точке (рис.74). Эквипотенциальную поверхность можно провести через лю бую точку поля. Следовательно, таких поверхностей может быть бесконечное множество. 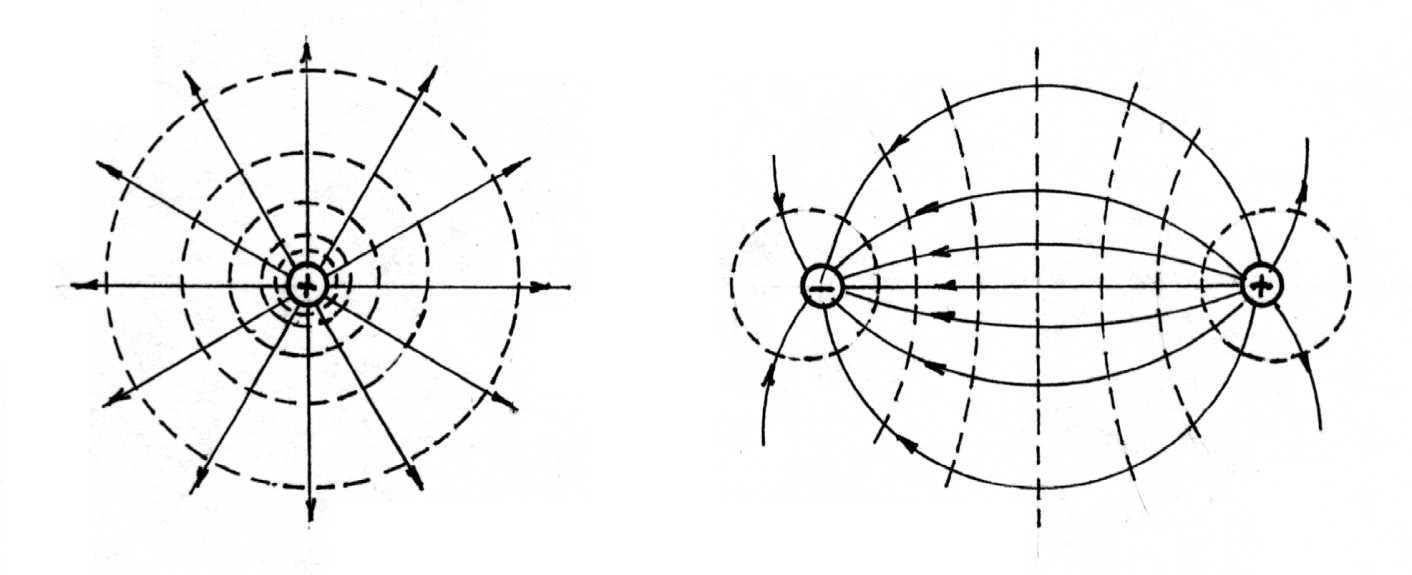 Рис. 74 Условились, однако, проводить их таким образом, чтобы разность потенциалов для двух соседних эквипотенциальных по верхностей была всюду одна и та же. Тогда по их густоте можно судить о величине напряженности поля. |