Краевое государственное автономное профессиональное образовательное учреждение Нытвенский многопрофильный техникум
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
Тема 9. Геометрические тела и поверхностиМногогранники, призма, параллелепипед. Свойства граней и диагоналей параллелепипеда. Пирамида, усечённая пирамида. Свойства параллельных сечений пирамиды. Цилиндрическая и коническая поверхности, тела вращения. Сечения цилиндра и конуса. Сфера и шар. Сечения шара плоскостью. Части сферы и шара. Плоскость, касательная к сфере, понятие о сферическом треугольнике. Вписанная в многогранник и описанная около многогранника сфера, определение её радиуса. Тема 10. Объёмы и площади поверхностей геометрических тел Объём параллелепипеда и призмы. Объём пирамиды, усечённой пирамиды. Объём цилиндра, конуса, усечённого конуса. Объём шара и его частей. Площадь поверхности призмы. Площадь поверхности пирамиды, усечённой пирамиды. Площадь поверхности цилиндра, конуса, усечённого конуса. Площадь сферы и её частей. Практические задания по курсу дисциплины «Математика». Степень с рациональным показателем. Вычислить: 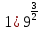 + + 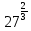 – – 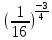 . .251,5 + (0,25) - 0,5 – 810,75. (0,36) – 0,5 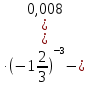 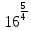 – – 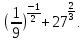 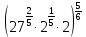 . .( 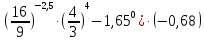 . .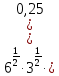 . .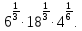 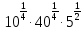 . .(0,49) – 1,5 ÷ 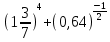 . .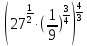 . .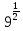 + + 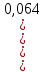 1,6) – 1 . 1,6) – 1 .91,5 – 810,5 – (0,5) – 2. 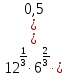 . . 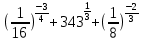 . .(0,04) – 1,5  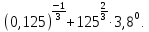 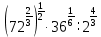  (0,25) - 0,5 +251,5– 810,75. 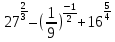 . .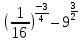 + + 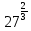 . .2. Применение непрерывности. Решить неравенства:
3. Показательная и логарифмическая функции.
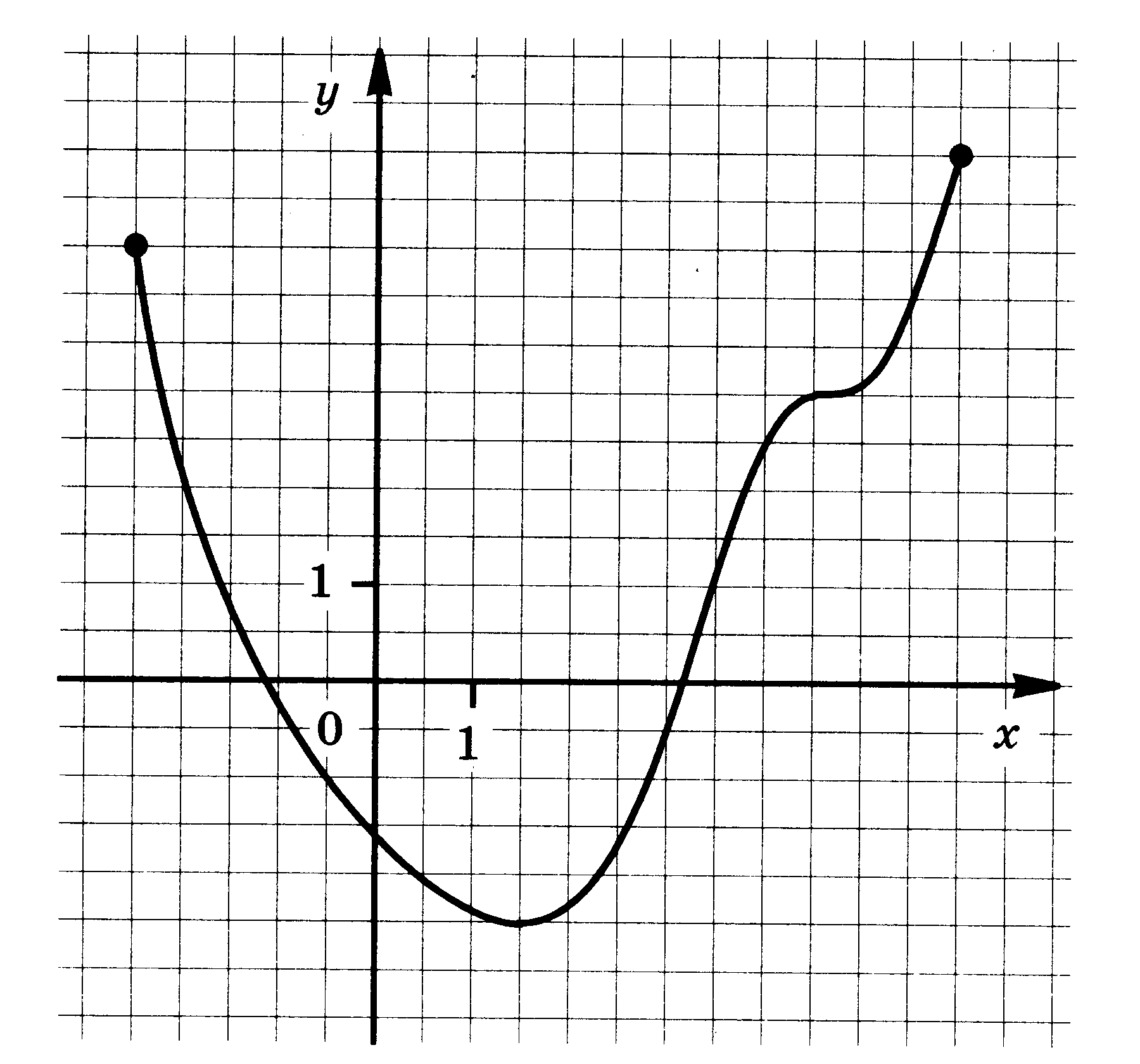
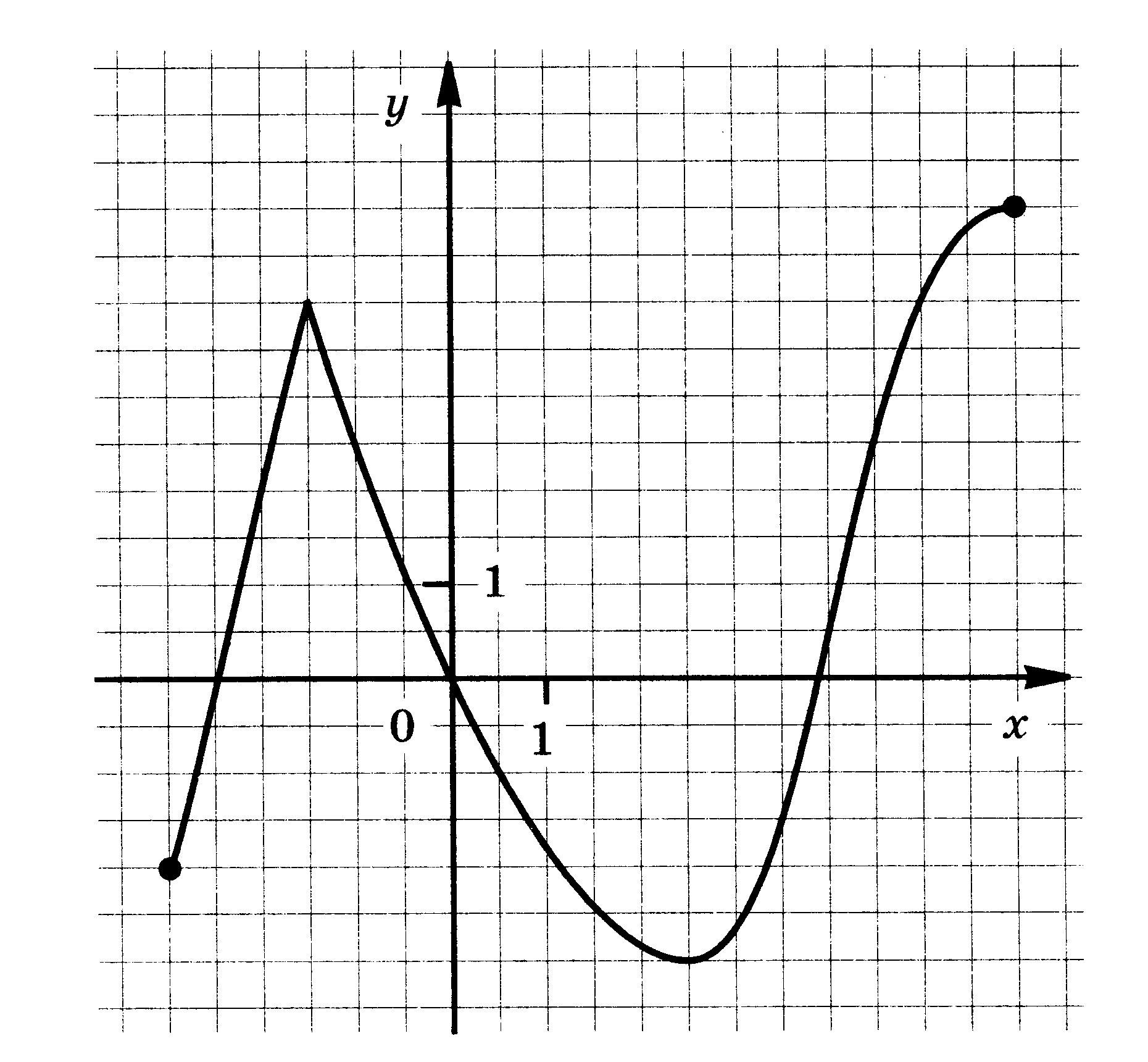
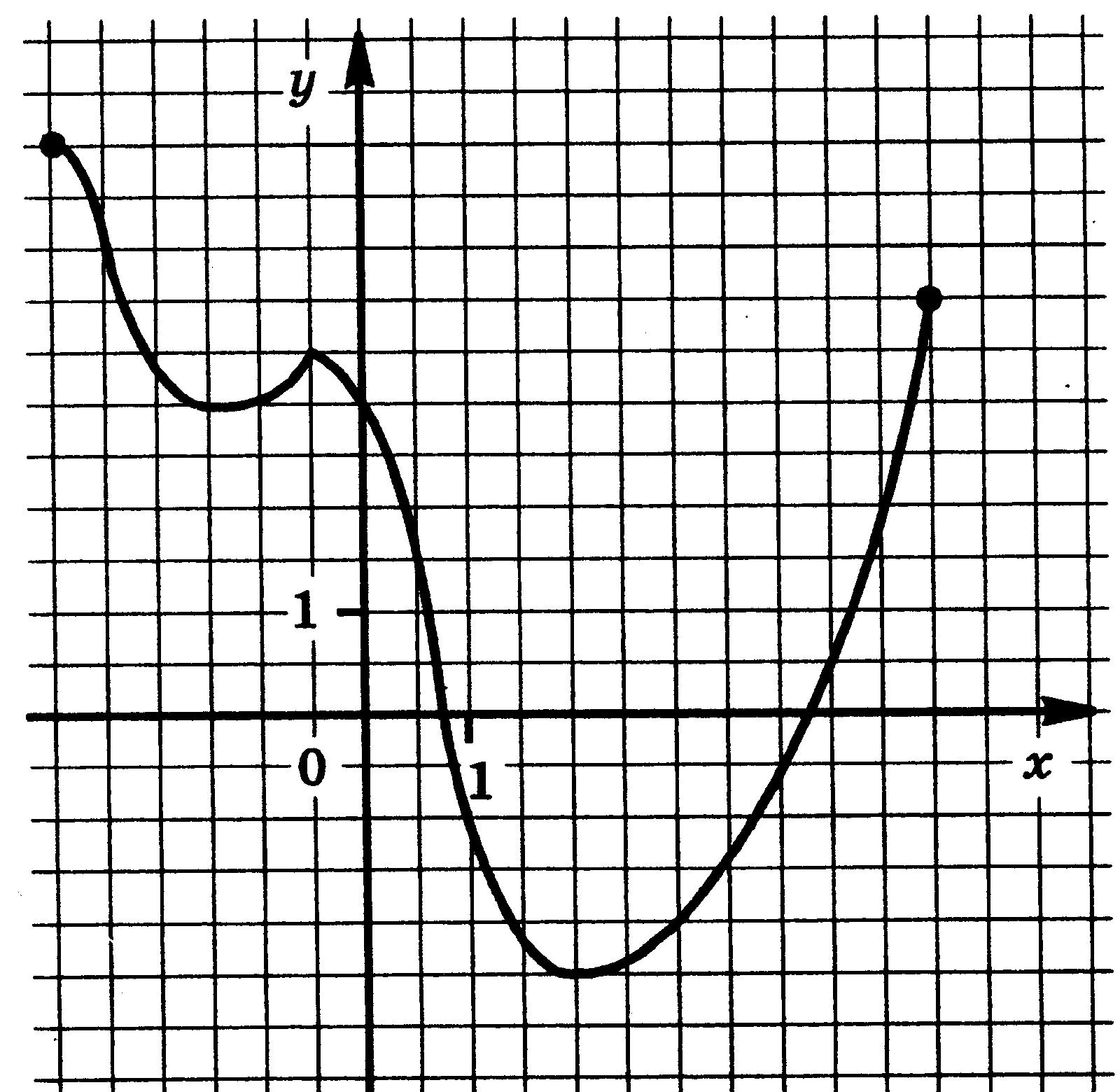
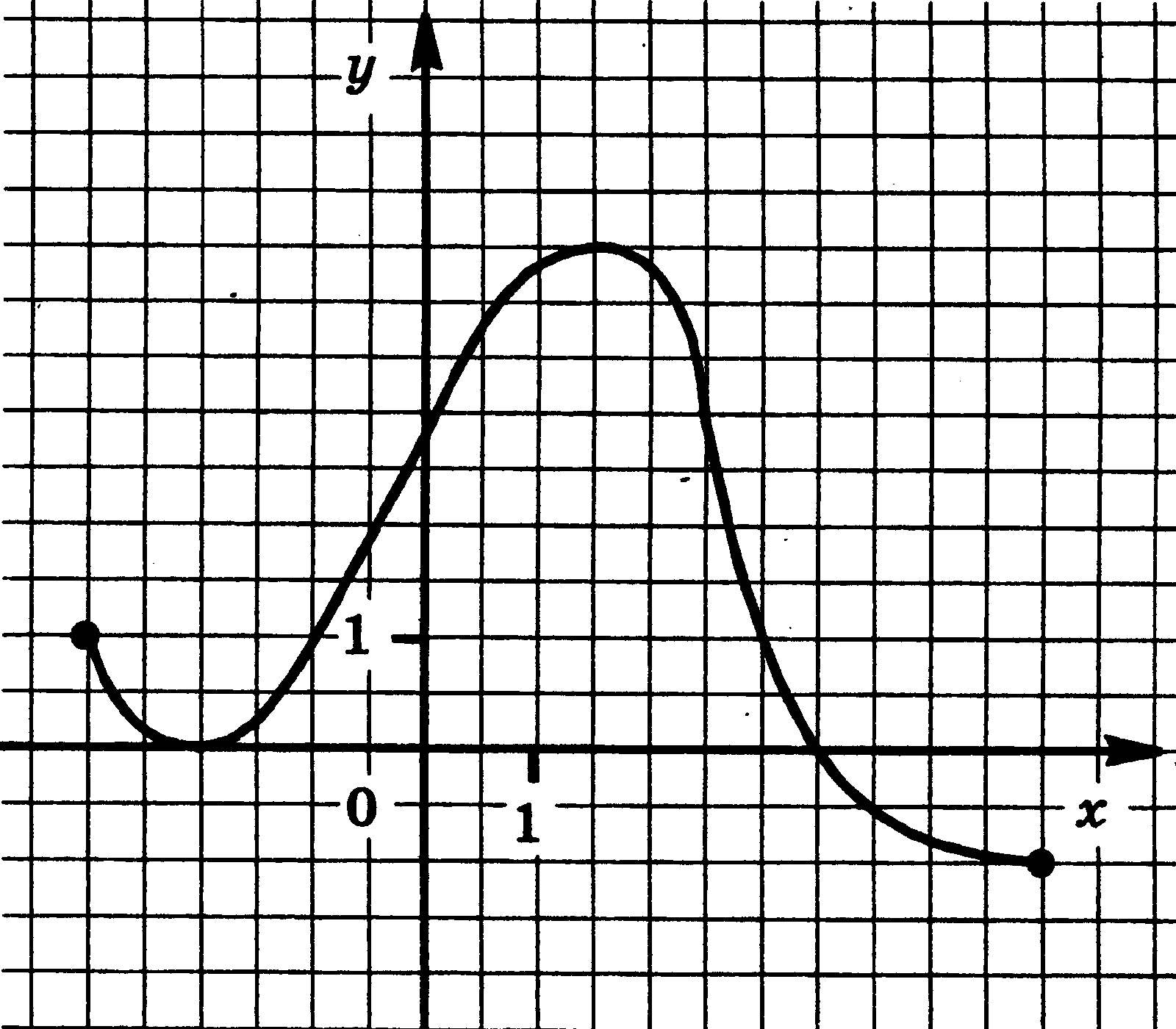
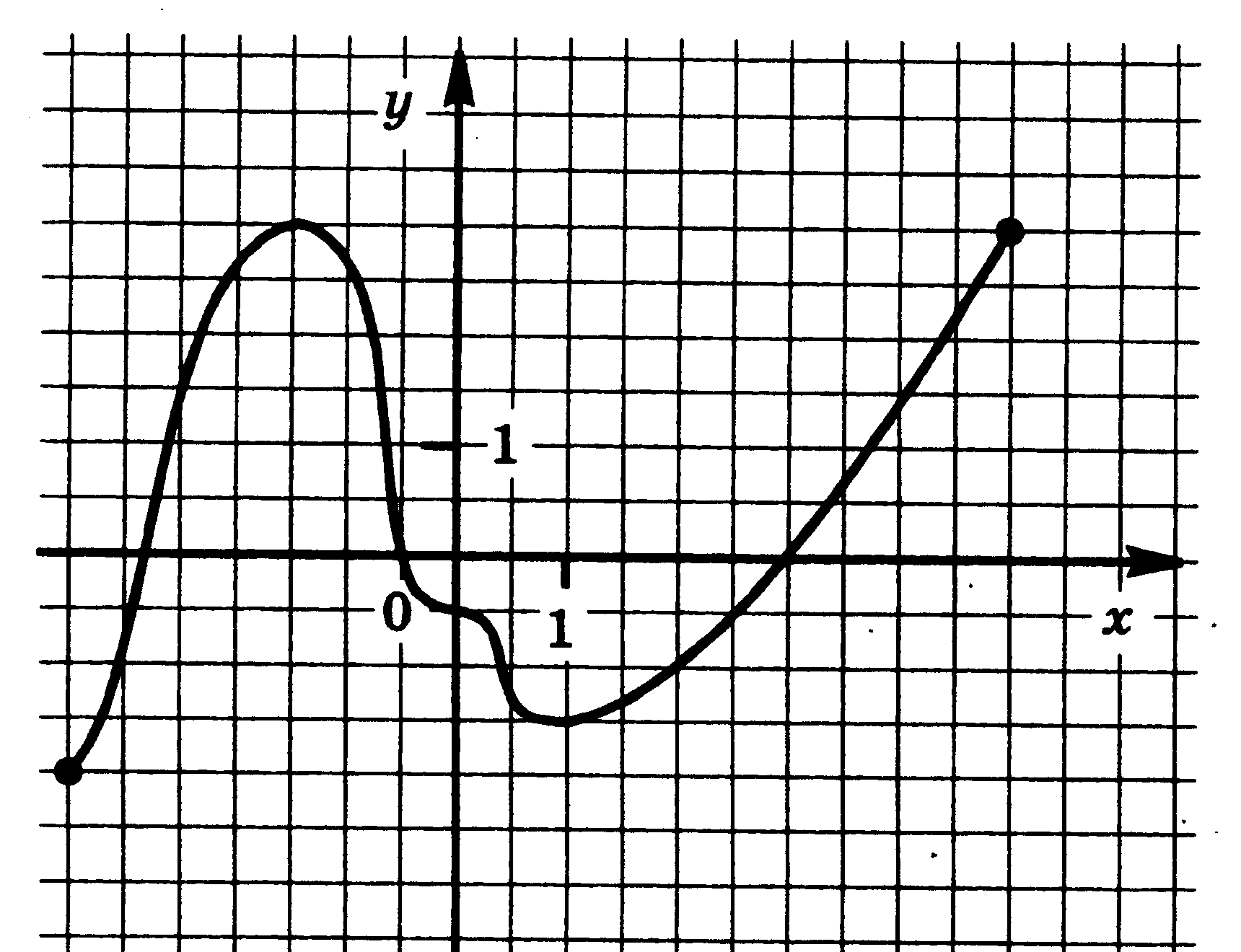
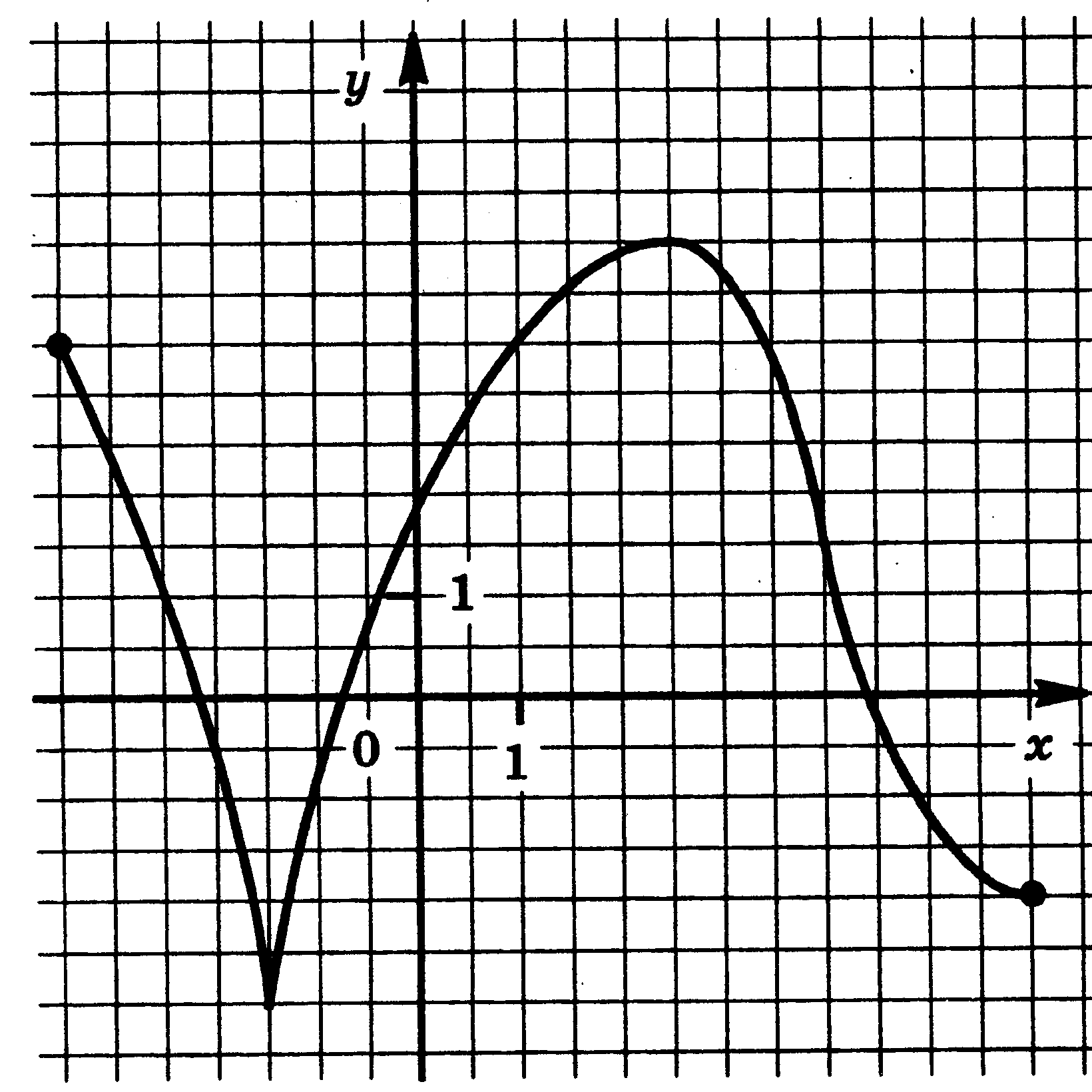
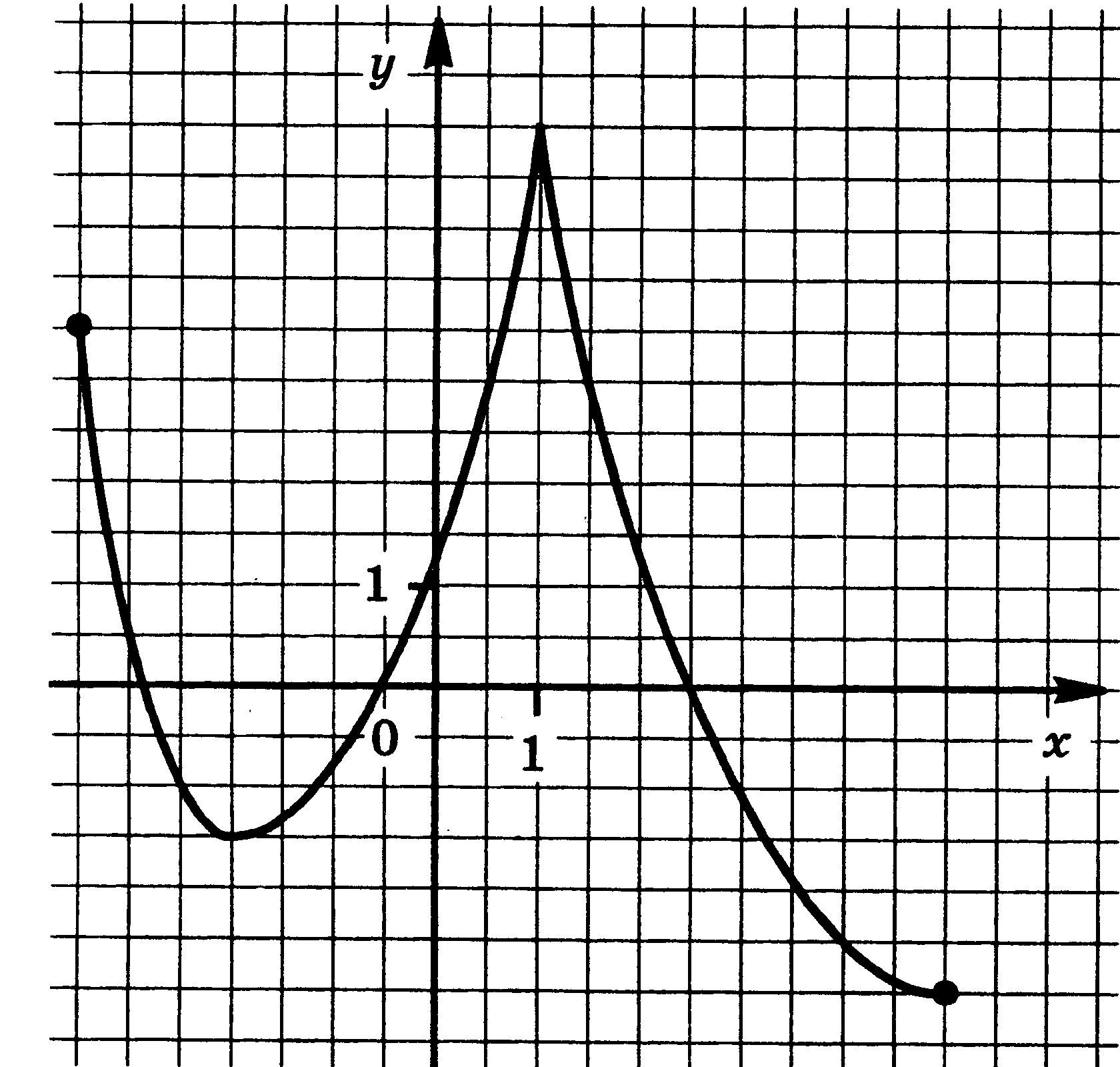
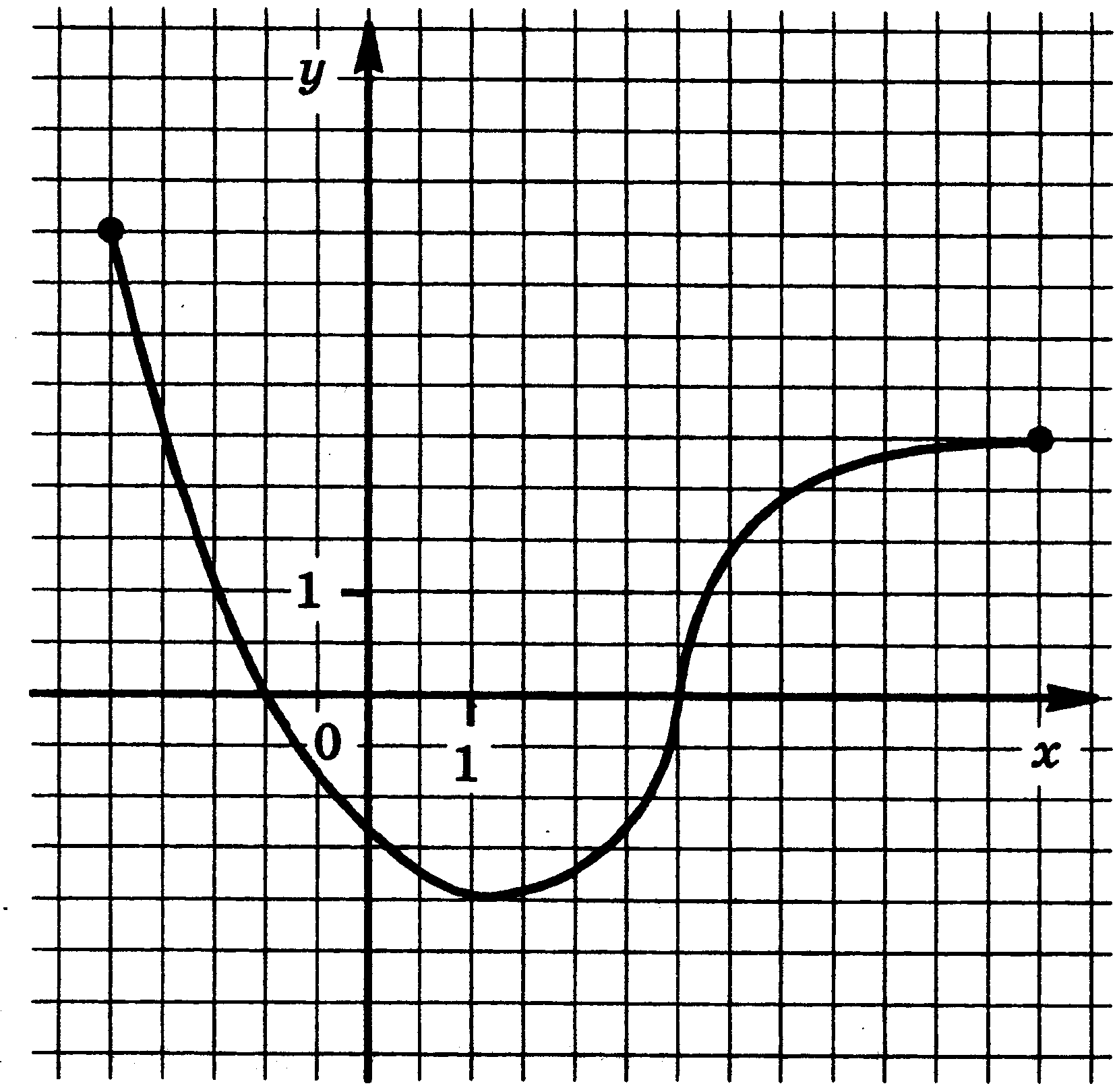
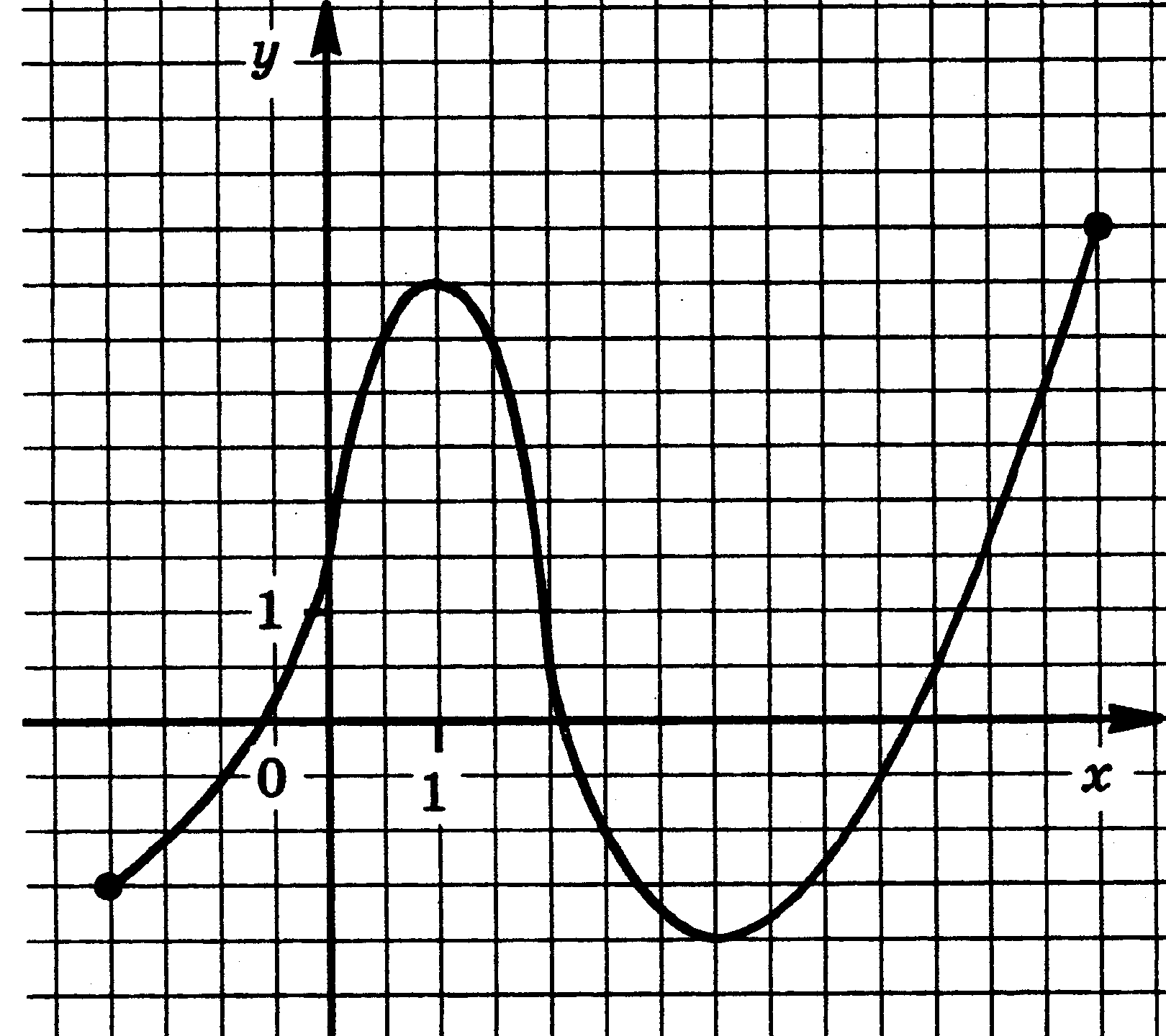
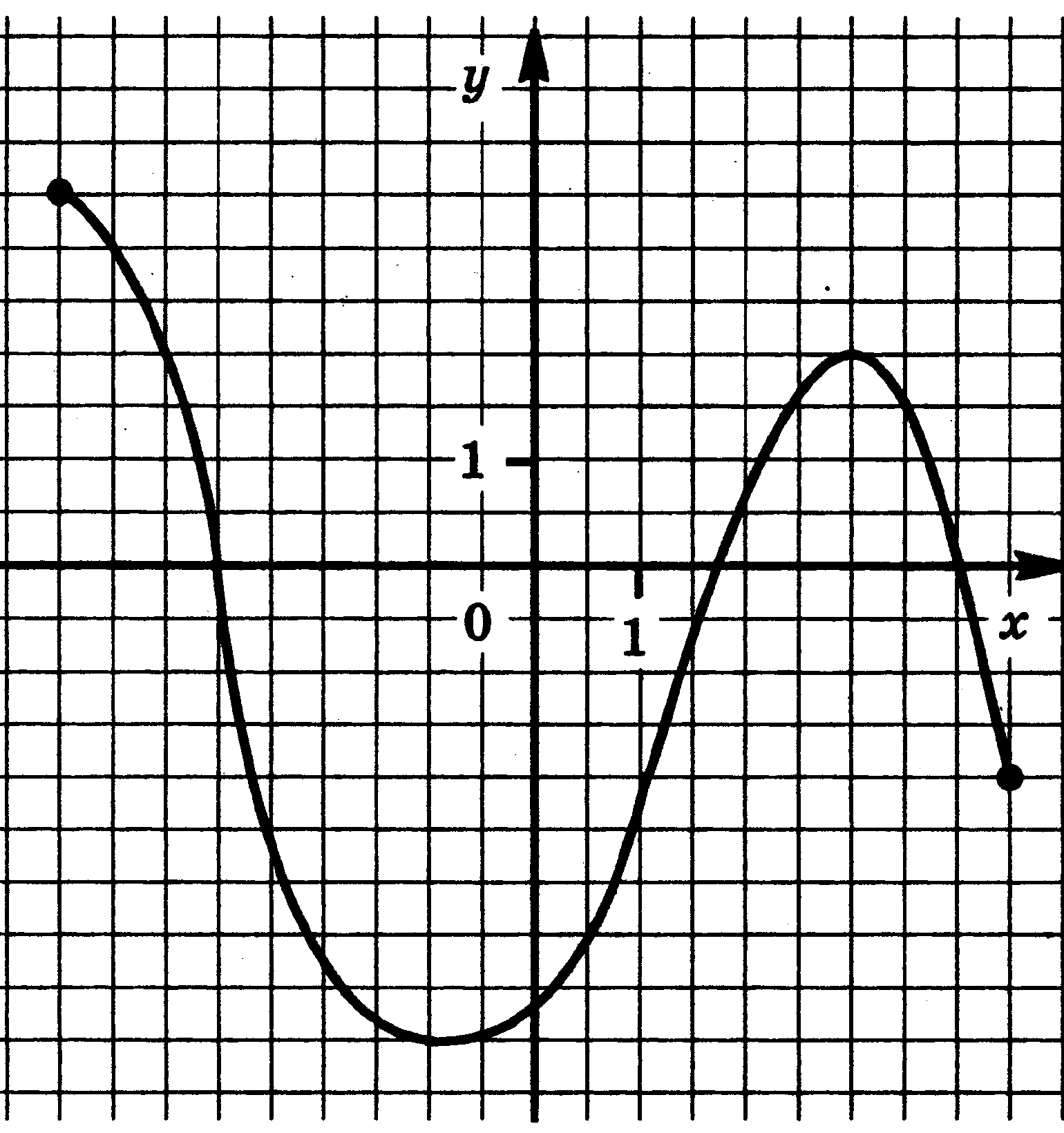
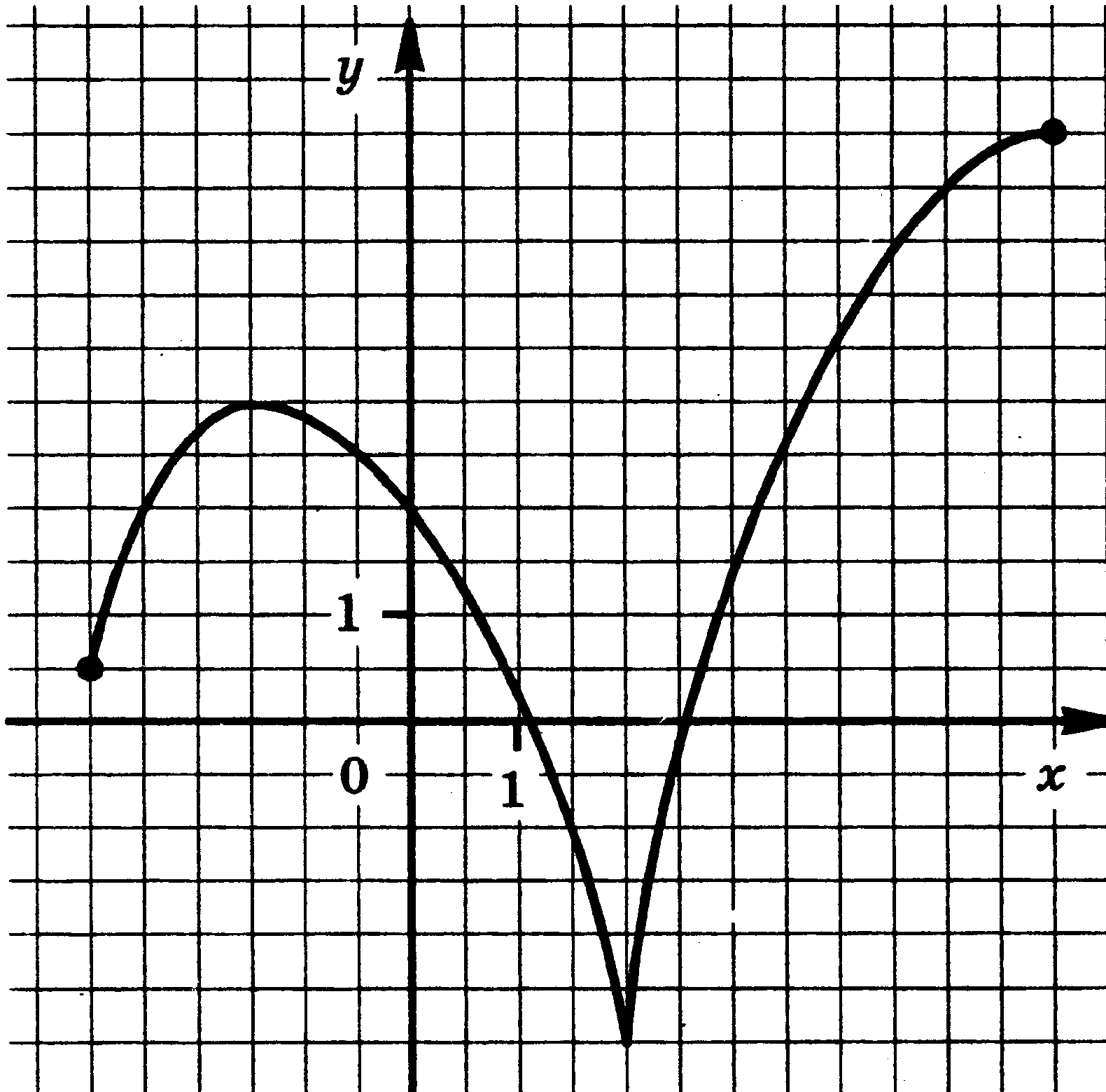
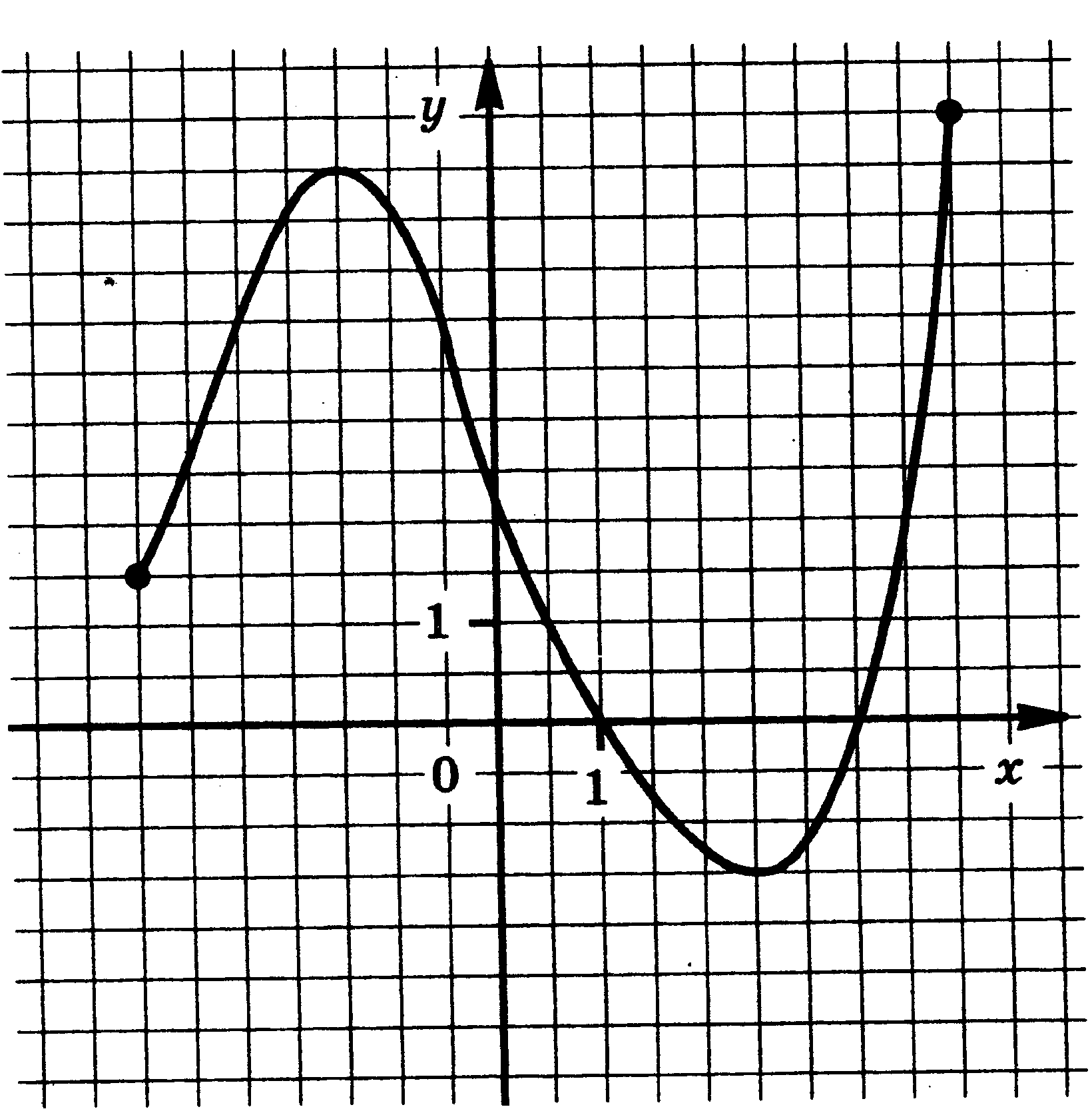
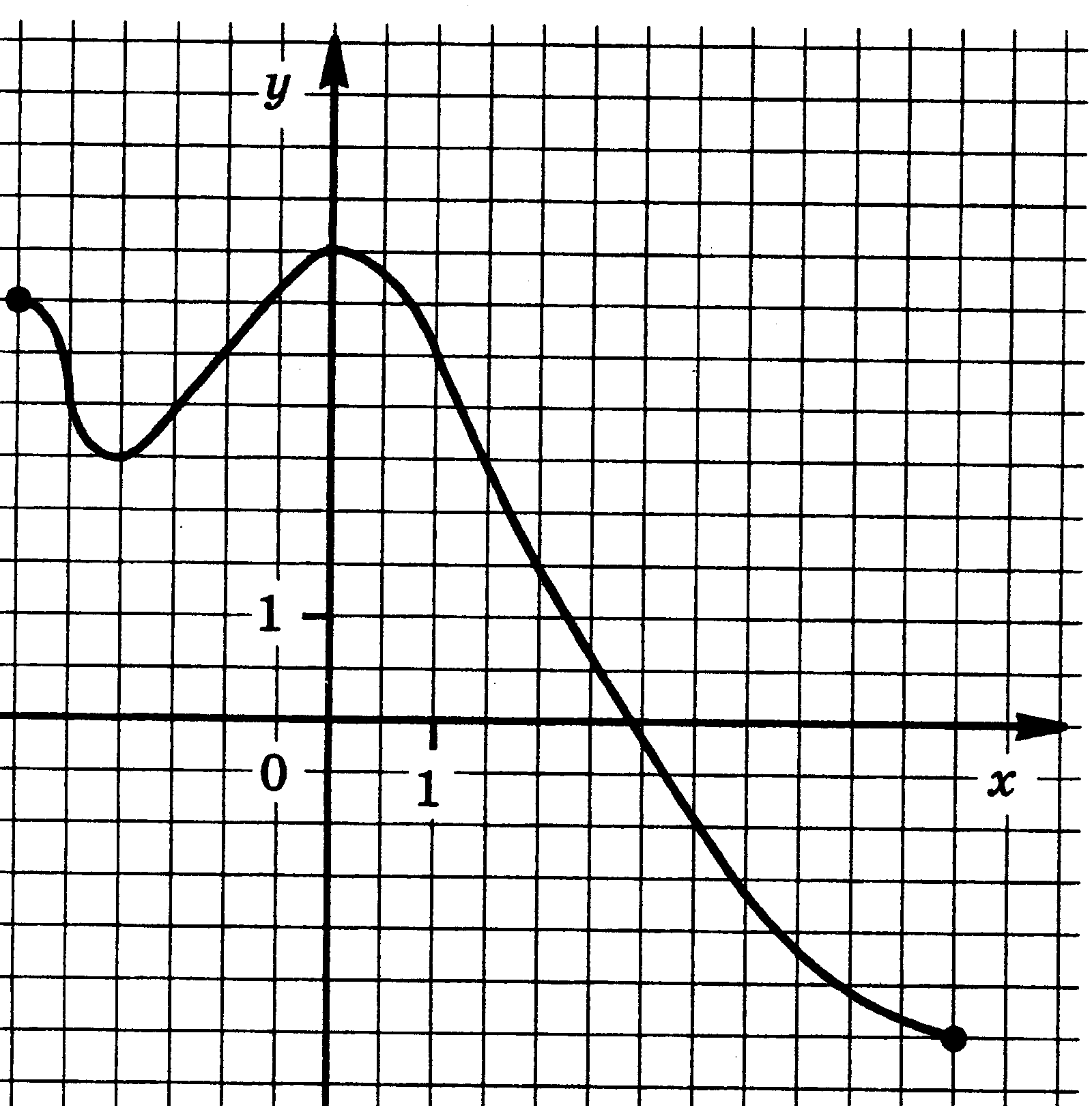
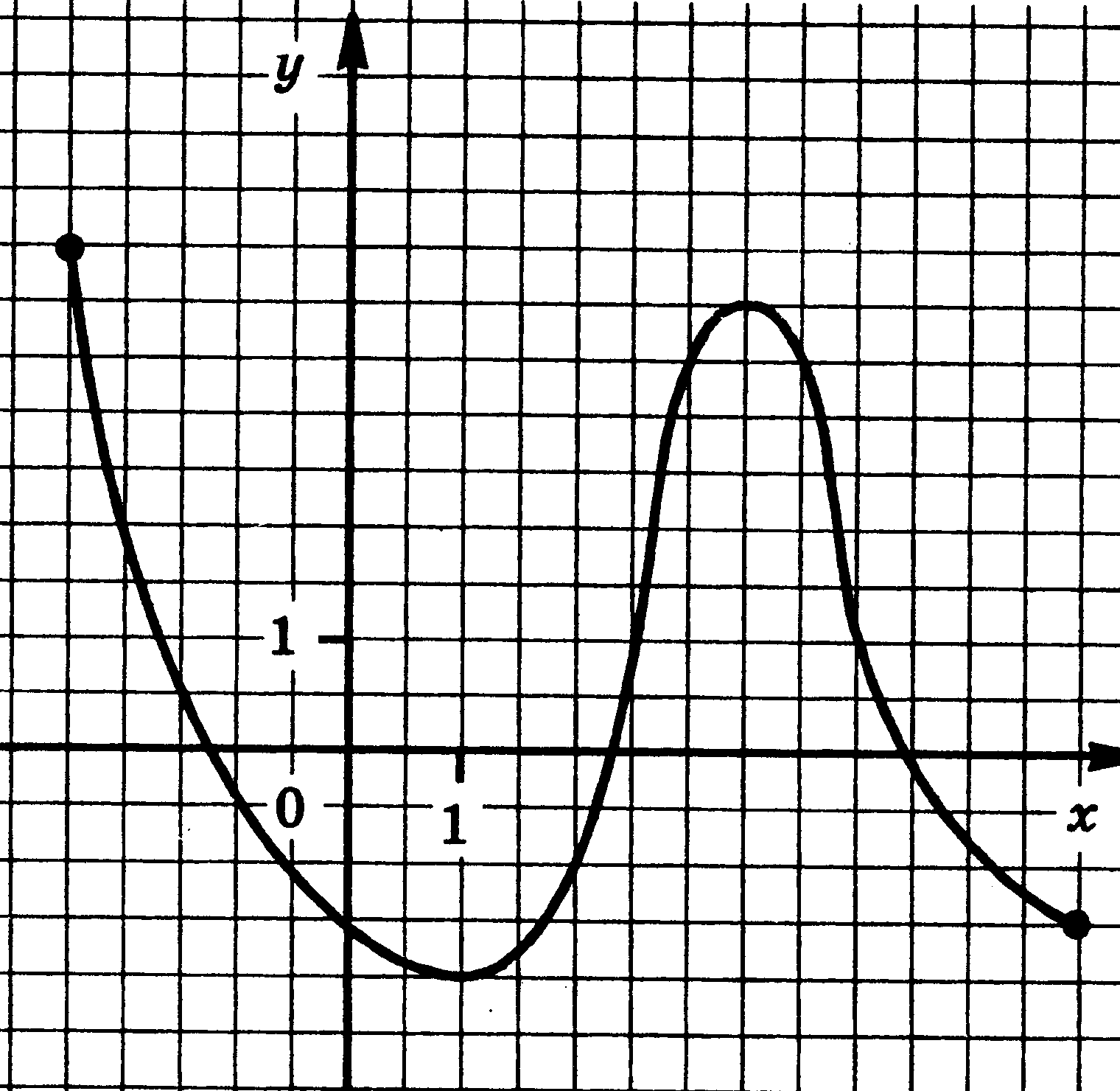
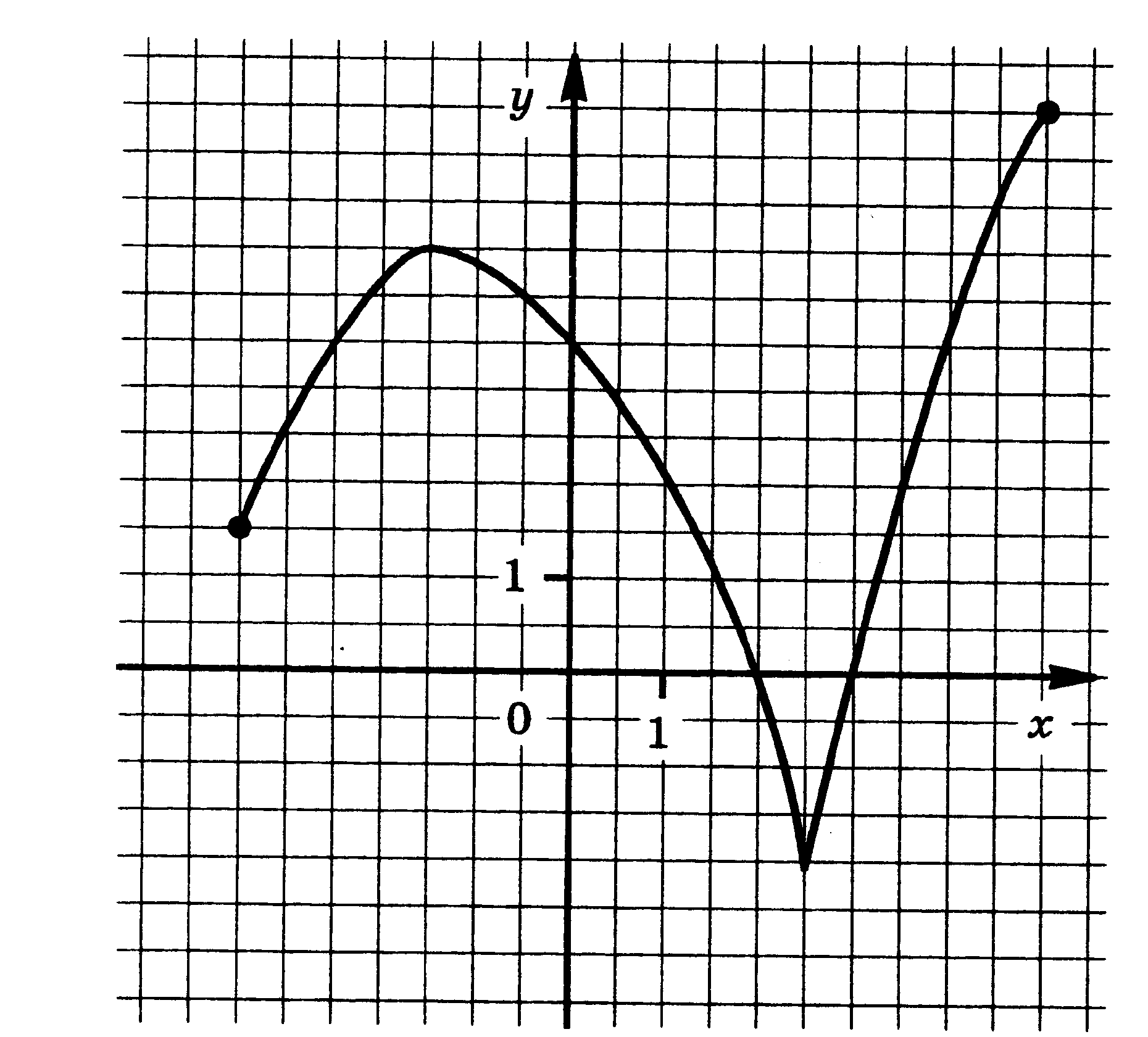
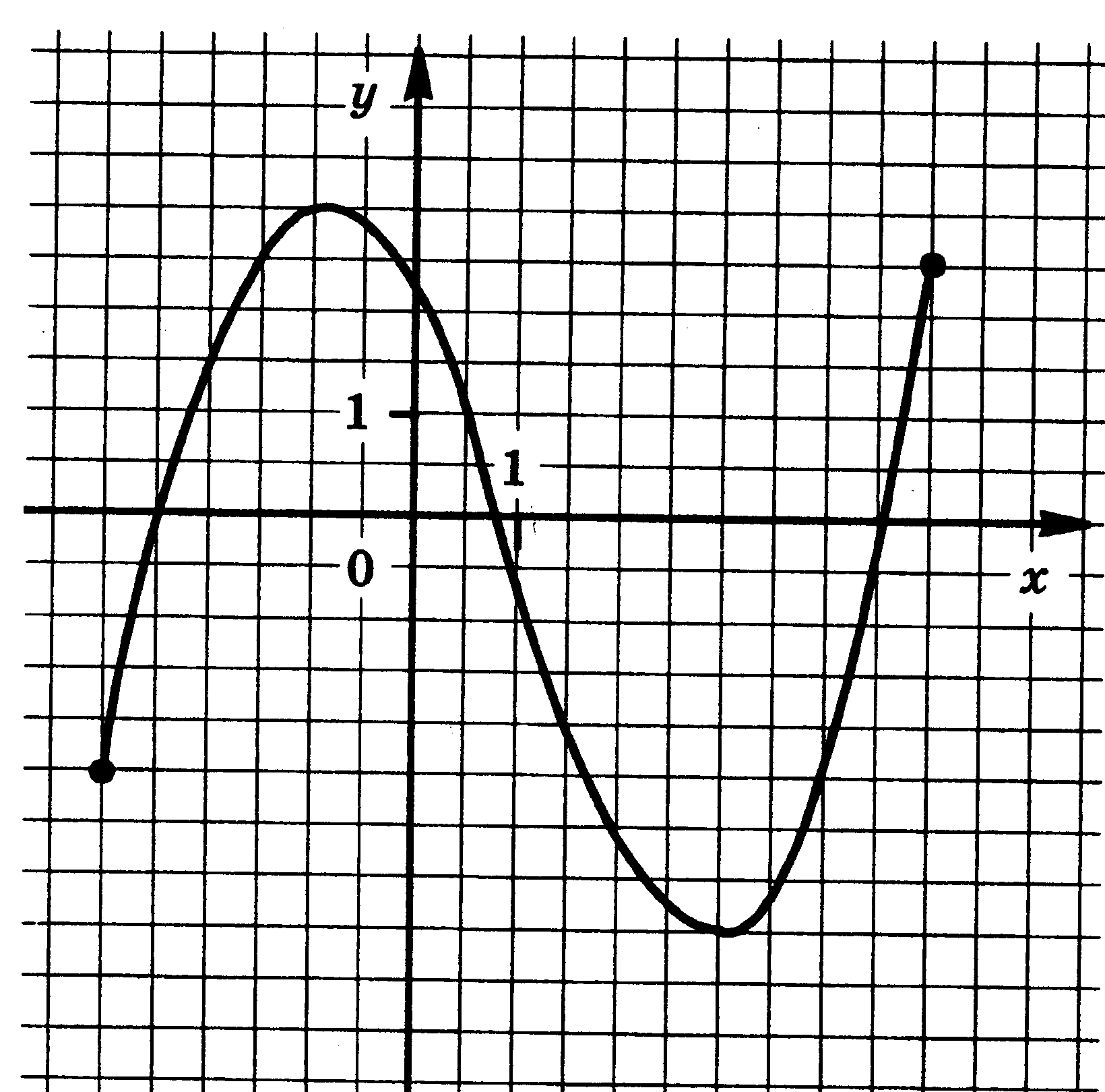
4. Функции: их свойства и графики. Функция у = f(x) задана своим графиком. Укажите: 1) область определения функции; 2) область значения функции; 3) нули функции; 4) интервалы знакопостоянства функции; 5) промежутки возрастания и промежутки убывания функции; 6) точки экстремума функции; 7) наибольшее и наименьшее значения функции.
5. Производная и ее применения. Найдите интервалы возрастания и убывания функции, определите вид точек экстремума:
6. Задачи планиметрии. Периметр треугольника ABC равен 20. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC. 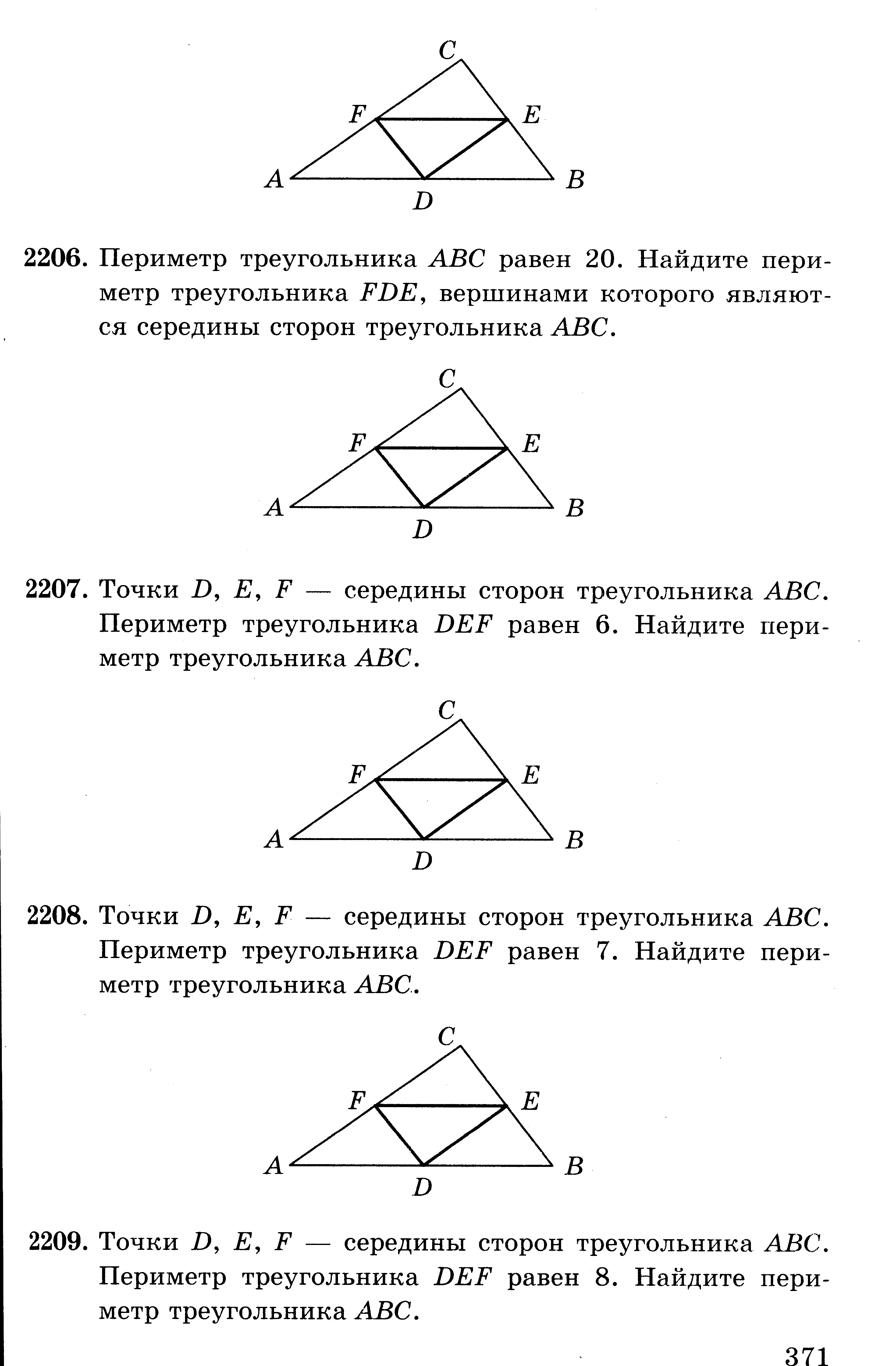 Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 6. Найдите периметр треугольника ABC.  Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 7. Найдите периметр треугольника ABC.  Точки D, Е, F — середины сторон треугольника ABC. Периметр треугольника DEF равен 8. Найдите периметр треугольника ABC.  Периметр треугольника ABC равен 16. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC  Периметр треугольника ABC равен 18. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC  Периметр параллелограмма равен 46 см. Меньшая сторона равна 9 см. Найдите большую сторону параллелограмма. Периметр параллелограмма равен 26 мм. Меньшая сторона равна 3 мм. Найдите большую сторону параллелограмма. Периметр параллелограмма равен 44 см. Меньшая сторона равна 10 см. Найдите большую сторону параллелограмма. Периметр параллелограмма равен 70 мм. Большая сторона равна 18мм. Найдите меньшую сторону параллелограмма. Периметр параллелограмма равен 54 см. Большая сторона равна 17см. Найдите меньшую сторону параллелограмма. Периметр параллелограмма равен 42 см. Большая сторона равна 19см. Найдите меньшую сторону параллелограмма. Середины последовательных сторон прямоугольника, диагонали которого равны 7дм, соединены отрезками. Найдите периметр образовавшегося четырехугольника. |

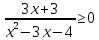
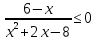
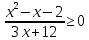
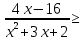 0
0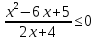
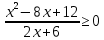
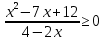
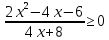
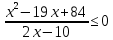
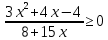
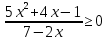
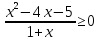
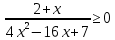
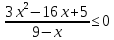
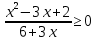
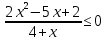
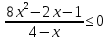
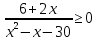
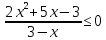
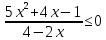
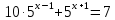
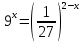
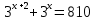 .
.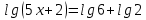
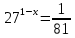
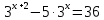
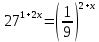
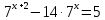
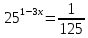
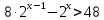
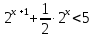
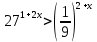
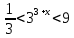
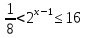
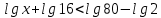
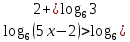
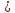 -3
-3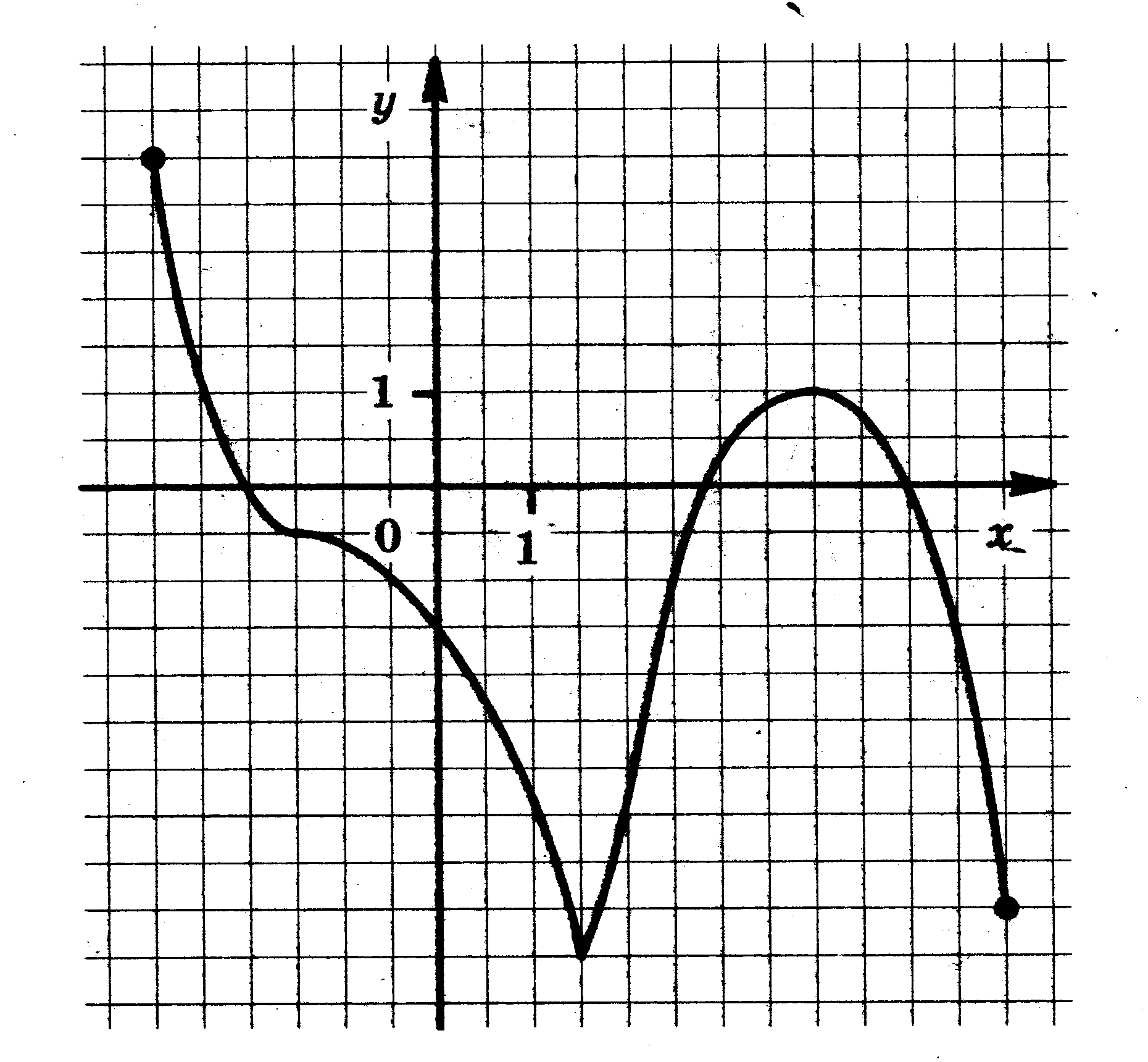
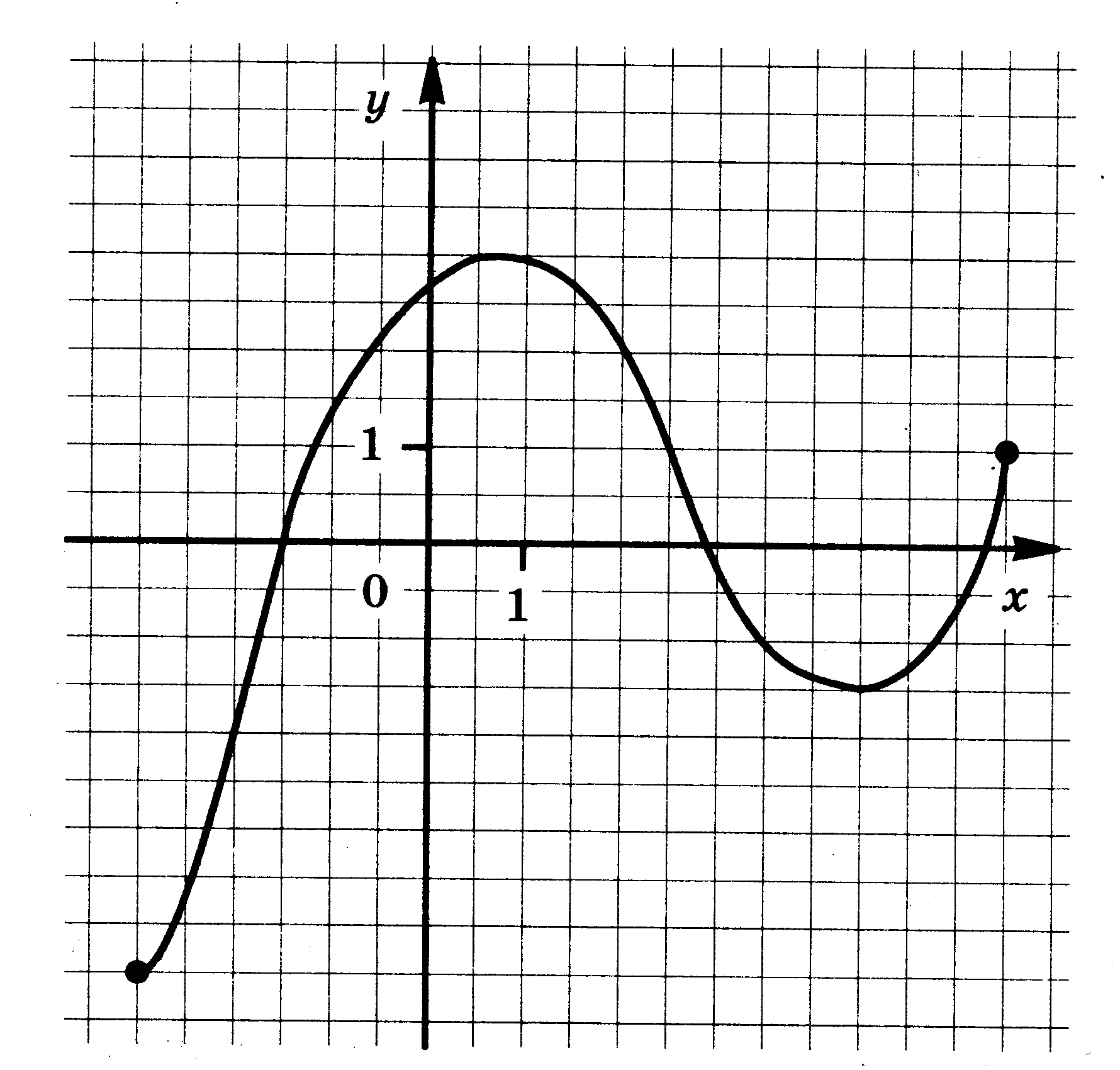
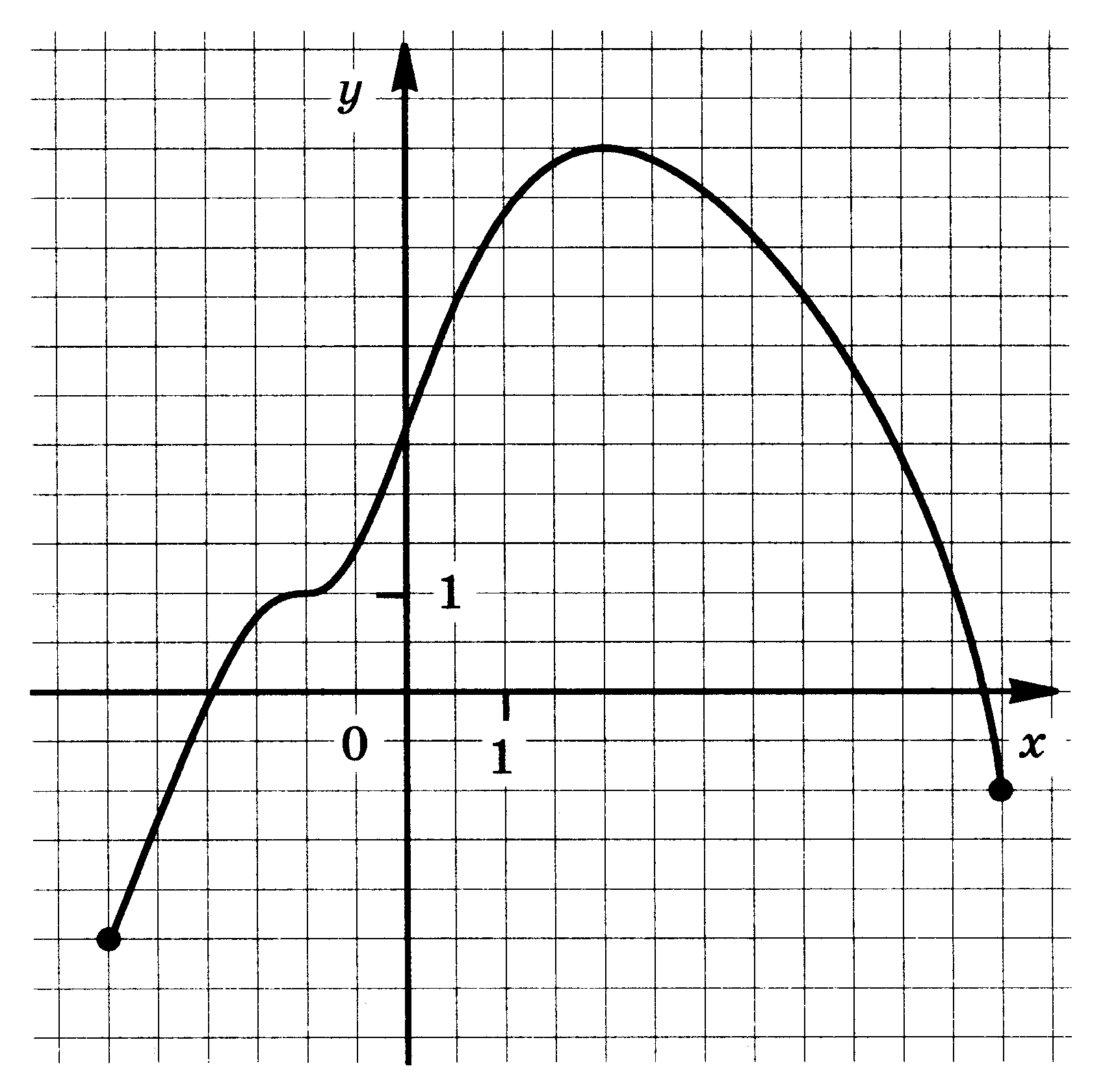
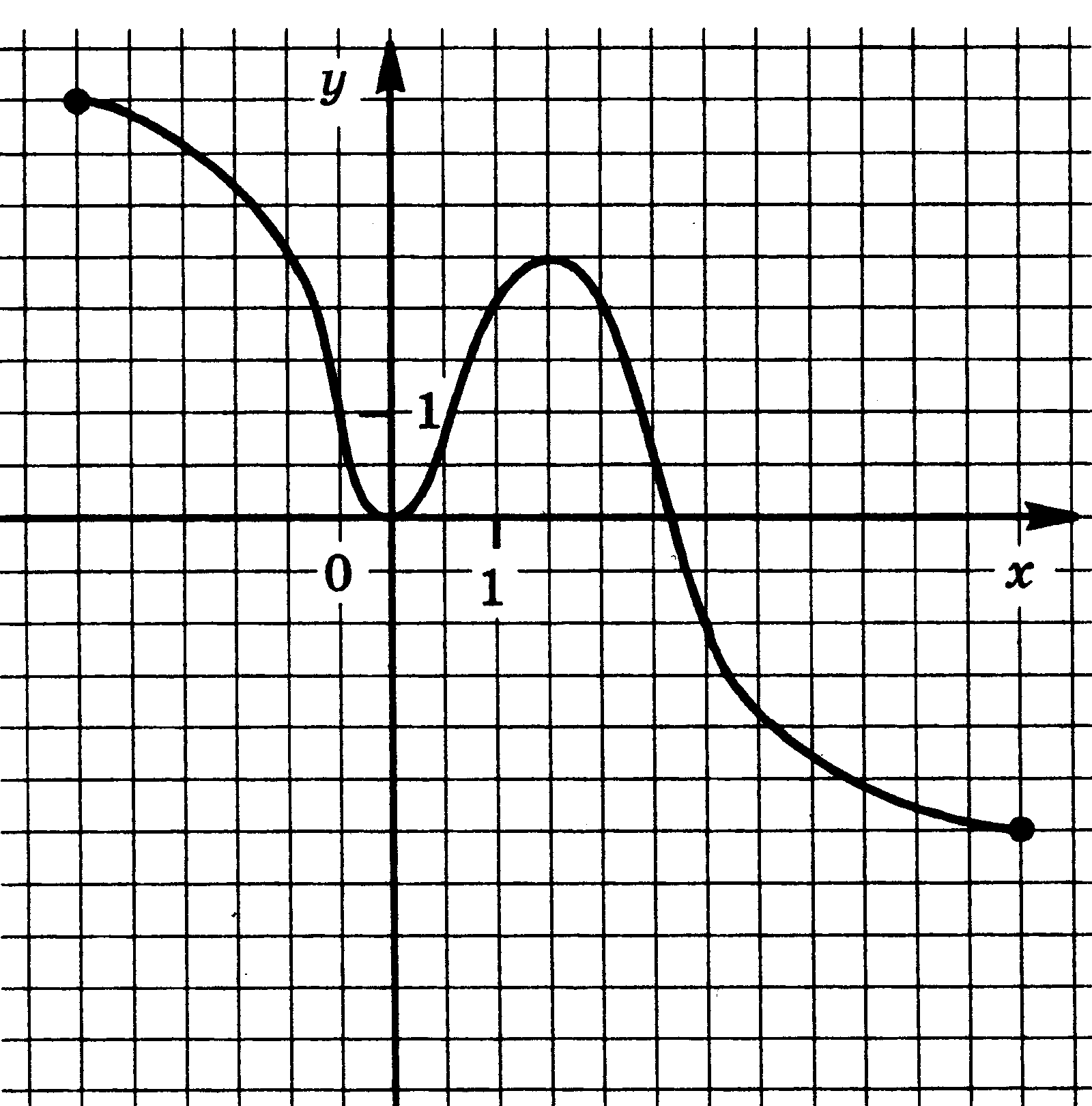
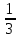 x3 + 5x2 – 1
x3 + 5x2 – 1 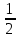 x4 – 8
x4 – 8