Краевое государственное автономное профессиональное образовательное учреждение Нытвенский многопрофильный техникум
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Краевое государственное автономное профессиональное образовательное учреждение «Нытвенский многопрофильный техникум» Задания для проведения итоговой аттестации по учебной дисциплине «Математика» для профессий среднего профессионального образования 35.01.14 «Мастер по техническому обслуживанию и ремонту машинно-тракторного парка» 15.01.25 «Станочник (металлообработка)» 19.01.17 «Повар, кондитер» Нытва 2015 Задания для проведения итоговой аттестации по учебной дисциплине «Математика» для профессий среднего профессионального образования 35.01.14 Мастер по техническому обслуживанию и ремонту машинно-тракторного парка; 15.01.25 Станочник (металлообработка); 19.01.17 Повар, кондитер составлены на основе Федерального государственного образовательного стандарта среднего общего образования (далее ФГОС СОО), рабочей программы учебной дисциплины МАТЕМАТИКА для профессий среднего профессионального образования Рассмотрено и одобрено на заседании П(Ц)К «___»________2015 г. _____С. П. Кашина Протокол № ____ Составитель: _____ преподаватель математики Кашина Светлана Павловна Проверка письменной работы и оценивание результатов итоговой аттестации. При проверке математической подготовки выпускников оценивается уровень сформированности следующих умений: выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; решать уравнения, простейшие системы уравнений, используя графики функций; вычислять производные и первообразные элементарных функций; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа; решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы; анализировать в простейших случаях взаимное расположение объектов в пространстве; изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач. При оценке работы обучающегося используется пятибалльная система. Результаты итоговой аттестации признаются удовлетворительными в случае, если обучающийся при сдаче работы по математике получил отметку не ниже удовлетворительной. Оценивание результата работы по математике осуществляется в соответствии со следующими рекомендациями: В случае прохождения аттестации в письменной форме задание считается выполненным верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. Для получения отметки "3" обучающийся должен правильно выполнить не менее пяти заданий, отметка "4" выставляется при выполнении семи-восьми заданий, отметка "5" ставится за девять или десять верно выполненных заданий. Преподаватель __________________ C.П.Кашина Рассмотрены на заседании П(Ц)К естественнонаучных и математических дисциплин Протокол № _____ от «___» _________________ 2015 г. Председатель П(Ц)К _____________ C.П.Кашина Теоретические вопросы по курсу дисциплины «Математика» Тема 1. Числовые системы и приближённые вычисления. Целые и рациональные числа. Действительные числа. Приближенные вычисления. Приближенное значение величины и погрешности приближений. Решение неравенств, уравнений первой и второй степени. 1.3 Решение квадратных уравнений с 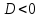 , двучленные уравнения. , двучленные уравнения.Тема 2. Функции, их свойства и графики. 2.5 Числовая функция, область определения, множество значений. 2.6 Свойства функции: чётность, нечетность, периодичность, ограниченность, монотонность, экстремум функции. 2.7 График функции. Простейшие преобразования графиков функций. 2.8 Приращение аргумента и приращение функции и их геометрический смысл. 2.9 Понятие предела функции в точке. Свойства пределов функций. 2.10 Понятие о бесконечно малых и бесконечно больших функциях. Предел функции на бесконечности. 2.11 Предел числовой последовательности. Монотонность, ограниченность и сходимость числовой последовательности. Число е. 2.12 Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных на отрезке. Тема 3. Показательная, логарифмическая и степенная функции. Степень с произвольным действительным показателем. Свойства степени. Степенная функция xn (для n = 2k, n = 2k + 1, n = – 1, – 2, 1/2, 1/3, – 1/2). Логарифмы и их свойства. Основное логарифмическое тождество. Формула перехода от логарифмов с одним основанием к логарифмам с другим основанием. Вычисление логарифмов с произвольным основанием. Логарифмирование и потенцирование выражений. Показательная функция, её свойства и график. Логарифмическая функция, её свойства и график. Решение показательных уравнений и неравенств. Решение логарифмических уравнений и неравенств. Тема 4. Тригонометрические функции. Тригонометрические функции числового аргумента и их простейшие свойства. Функция y = sinx, её свойства и график. Функция у = соsx, её свойства и график. Функция y = tgx, её свойства и график. Зависимость между тригонометрическими функциями одного аргумента. Формулы приведения. Теоремы сложения и следствия из них. Решение уравнений sinx = 0, cosx = 0, tgx = 0, sinx = 1, cosx = 1, sinx = – 1, cosx = – 1. Обратные тригонометрические функции, их простейшие свойства. Простейшие тригонометрические уравнения и их решение. Тригонометрическая и показательная формы комплексного числа, переход от одной формы записи комплексных чисел к другой. Действия над комплексными числами в тригонометрической и показательной формах. Тема 5. Векторы и координаты на плоскости и в пространстве. Скалярные и векторные величины. Векторы. Линейные операции над векторами. Разложение вектора по двум неколлинеарным векторам на плоскости, по трём некомпланарным векторам в пространстве. Скалярное произведение векторов и его свойства. Угол между векторами. Деление отрезка в данном отношении. Уравнения прямой на плоскости: с нормальным вектором, с направляющим вектором, параметрические уравнения прямой. Уравнения прямой, проходящей через данную точку с заданным угловым коэффициентом, проходящей через две данные точки. Общее уравнение прямой и его исследование, уравнение прямой в отрезках. Угол между прямыми, условия параллельности и перпендикулярности прямых. Тема 6. Прямые и плоскости в пространстве Прямая и плоскость в пространстве. Признак параллельности прямой и плоскости. Обратная теорема. Две плоскости в пространстве. Признак параллельности двух плоскостей. Перпендикуляр и наклонные к плоскости. Угол прямой с плоскостью. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. Теорема о трёх перпендикулярах. Двугранный угол, линейный угол двугранного угла. Понятие о многогранном угле. Теорема о плоском угле трёхгранного угла. Перпендикулярность плоскостей. Признак перпендикулярности плоскостей. Обратная теорема. Тема 7. Производная и её приложения Задача, приводящая к понятию производной, физический смысл производной. Нахождение производной функции по определению. Геометрический смысл производной. Алгоритм отыскания уравнений касательной к данной кривой. Формулы дифференцирования: константы, аргумента, степени, суммы, произведения, частного. Понятие сложной функции. Дифференцирование сложной функции. Дифференцирование логарифмических и показательных функций. Дифференцирование тригонометрических функций. Дифференцирование обратных тригонометрических функций. Применения производной. Тема 8. Интеграл и его приложения Первообразная. Неопределённый интеграл и его свойства. Интегрирование элементарных функций. Табличные интегралы. Метод подстановки в неопределённом интеграле. Задачи, приводящие к понятию определённого интеграла. Определённый интеграл и его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбница. |
