Краткая теория для выполнения лабораторных работ по курсу оту
 Скачать 11.96 Mb. Скачать 11.96 Mb.
|
|
Федеральное Агентство по Образованию Государственное Образовательное Учреждение Высшего Профессионального Образования Обнинский Государственный Технический Университет Атомной Энергетики Кафедра АКиД Краткая теория для выполнения лабораторных работ по курсу ОТУ. 2008 г. Содержание стр Введение 3 1. Классификация систем автоматического регулирования 3 5. Принципы автоматического регулирования 14 Принцип управления по внешнему возмущению 15 Принцип управления по отклонению 15 Комбинированное управление 15 6. Анализ устойчивости САР 16 Матрица коэффициентов 18 6.3. Частотные критерии 19 7. Качество процессов автоматического управления. 23 Краткая теория ВведениеТАУ (теория автоматического управления)– это научная и техническая дисциплина, она изучает общие принципы системной организации на основе построения математических моделей объектов и систем управления. Это позволяет оценивать характеристики и свойства проектируемых систем, создавать системы, отвечающие заданным требованиям качества. Анализ - исследование системы управления, путем построения ее математической модели и изучения свойств этой модели. Анализ проводится с целью выяснения вопроса о том, способна ли в принципе модель САР решать задачу управления, и если нет, то какими методами и средствами ее можно сделать работоспособной. Синтез – (теоретическое конструирование) – это построение модели системы управления, обеспечивающей требуемое поведение объекта управления. Этапы проектирования системы управления
1. Классификация систем автоматического регулированияI. Классификация по характеру изменения величин:
II. Классификация по математическим признакам:
III. Классификация по типу ошибки в статике:
IV. Классификация по алгоритмам функционирования (по назначению):
V. По виду цикла управления:
VI. По принципу управления:
VII. По наличию или отсутствию вспомогательной энергии:
2. Основные понятия Объект управления (ОУ) в ТАУ – это устройство, машина или процесс и др., которые характеризуются некоторыми физическими величинами. Эти величины могут быть измерены. Объект управления способен воспринимать внешние воздействия и реагировать на них изменением значений выходных величин. Объектами управления в технике могут быть машины, механизмы, электромеханические устройства, более простые САР и др.  Рис.1 Обозначение объекта управления (ОУ) на функциональной схеме. x(t) - воздействие на объект, y(t) – реакция объекта, отклик на воздействие С точки зрения ТАУ не так важно, из каких физических элементов состоит объект управления (ОУ), куда важнее знать, как объект реагирует на внешние воздействия. Различают статический и динамический режимы работы объекта или системы управления. В статике все сигналы (воздействия и реакции) постоянны, инерционность элементов САР не проявляется. В динамике воздействия, а следовательно и отклики, реакции объектов и систем, изменяются, что приводит к проявлению инерционных свойств объектов. Статическая характеристика – зависимость выходной величины объекта у, т.е. величины характеризующей объект управления, от величины подаваемого на его вход воздействия х, при условии, что подаваемое воздействие постоянно, т.е. х = const. При малых изменениях воздействий, как правило, любой объект является линейным. Т.е. малые изменения воздействий приводят к малым изменениям реакций, пропорциональным изменению воздействий. 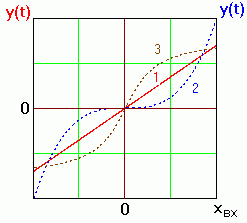 Рис. 2 Примеры статических характеристик объектов управления. 1 – линейная характеристика; 2,3 – нелинейные характеристики Характеристики объекта:
Свойства объекта:
Функциональная схема состоит из блоков соответствующих функциональным, физически существующим элементам объектов, а стрелки указывают на направление передачи энергии между ними. Пример: 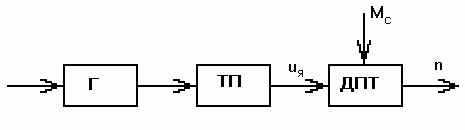 Рис.3 Пример функциональной схемы. Г – генератор; ТП – тиристорный преобразователь; ДПТ – двигатель постоянного тока Структурная (структурно-алгоритмическая) схема – состоит из звеньев, соответствующих математическим операциям преобразования сигналов; стрелки между блоками указывают направление передачи информации (сигналов). Пример: 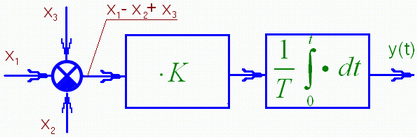 Рис. 4 Фрагмент структурной схемы. Показаны сумматор, пропорциональное звено и интегратор. Замечание: в структурной схеме в блок может входить только одна стрелка, за исключением сумматора и перемножителя сигналов. Примечание. Функциональная схема объекта единственна и может отличаться лишь глубиной, подробностью отображения элементов объекта. Структурных схем для одного и того же объекта может быть составлено несколько разных, причем все они будут эквивалентны между собой. Структурная схема – это особого вида математическая модель объекта или системы управления. Замкнутая САР с управлением по отклонению Схема используется для слежения, программного управления и стабилизации. В такой системе регулятор в процессе управления учитывает как задание, так и реальное состояние объекта, а, кроме того, косвенно учитывает и возмущение. 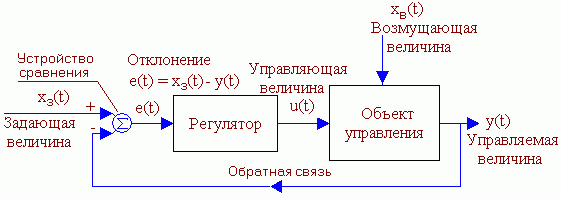 Рис. 5 Функциональная схема замкнутой САР с управлением по отклонению. e(t) – отклонение (ошибка слежения, регулирования) управляемой величины y(t) от задания хз(t). Основные элементы схемы: объект управления, контур главной обратной связи Сравнивающее устройство (сумматор) сравнивает задающую и управляемые величины и вычисляет отклонение, ошибку e(t) = хз(t) - y (t). Регулятор – вырабатывает такое управляющее воздействие u(t) на объект управления, которое сводит ошибку к нулю или допустимому минимуму. В идеале, когда e = 0, хз(t) = y (t) Системы автоматического регулирования предназначены для того, чтобы поддерживать управляемую величину объекта пропорциональной задающей величине с требуемой точностью. Т.о., закон изменения во времени задания повторяется управляемой величиной. Задание, как правило, маломощный сигнал. САР позволяет с помощью этого маломощного сигнала управлять мощным объектом. 3.Типовые динамические звенья Типовые звенья Это простые модели элементов сложных линейных систем и даже систем вцелом. Переходная характеристика звеньев Переходная характеристика или функция позволяет и качественно, и количественно характеризовать быстродействие звеньев и систем. Переходный процесс может быть как монотонным, так и колебательным и его длительность и является количественной характеристикой быстроты реакции звена на прикладываемые к нему воздействия. Типовые звенья бывают:
Основные характеристики линейных звеньев:
Типовые звенья линейных систем можно определять различными эквивалентными способами, в частности с помощью, так называемой передаточной функции, имеющей, как правило, дробно-рациональный вид, т.е. представляющей собой отношение двух полиномов: 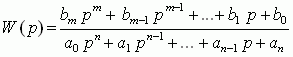 где bi и aj – коэффициенты полиномов. Это т.н. параметры передаточной функции или звена. Передаточная функция – это отношение изображения Y(p) выходного сигнала y(t) звена к изображению X(p) его входного сигнала x(t). 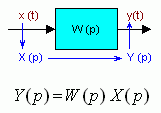 Т.е., передаточная функция позволяет по любому известному входному сигналу x(t) найти выходной y(t). Это значит, что с точки зрения ТАУ передаточная функция полностью характеризует систему управления или ее звено. Это же самое можно сказать и в отношении совокупности коэффициентов полиномов числителя и знаменателя передаточной функции. Наличие нулевых корней в числителе или знаменателе передаточной функции типовых звеньев - это признак для разбиения последних на три группы:
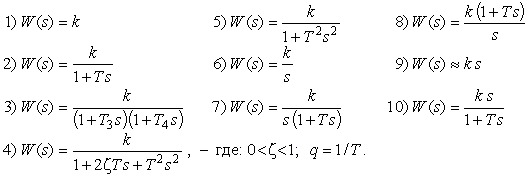 Переходные и весовые характеристики основных типовых звеньев приведены в Таблице 1. Перечисленные линейные звенья содержат один вход и один выход. Существует еще одно линейное звено, которое может иметь несколько, больше одного, входов и один выход: сумматор. Сумматор - необходимое звено для построения модели достаточно сложной системы, состоящей из нескольких звеньев. Типовых звеньев всего около полутора десятков, но из них, как из кубиков (или, если угодно, как любое сложное вещество из отдельных химических элементов), можно построить модель линейной системы управления любой сложности. Минимальный набор звеньев, который позволяет построить модель линейной системы любой сложности, в том числе и самих типовых звеньев, состоит всего из трех звеньев: пропорционального, интегратора и сумматора. Однако модель, построенную из этих трех звеньев, бывает труднее анализировать, чаще удобнее применять кроме них еще несколько типов звеньев. Таблица 1. Передаточные, переходные и весовые функции типовых звеньев. 1. Позиционные 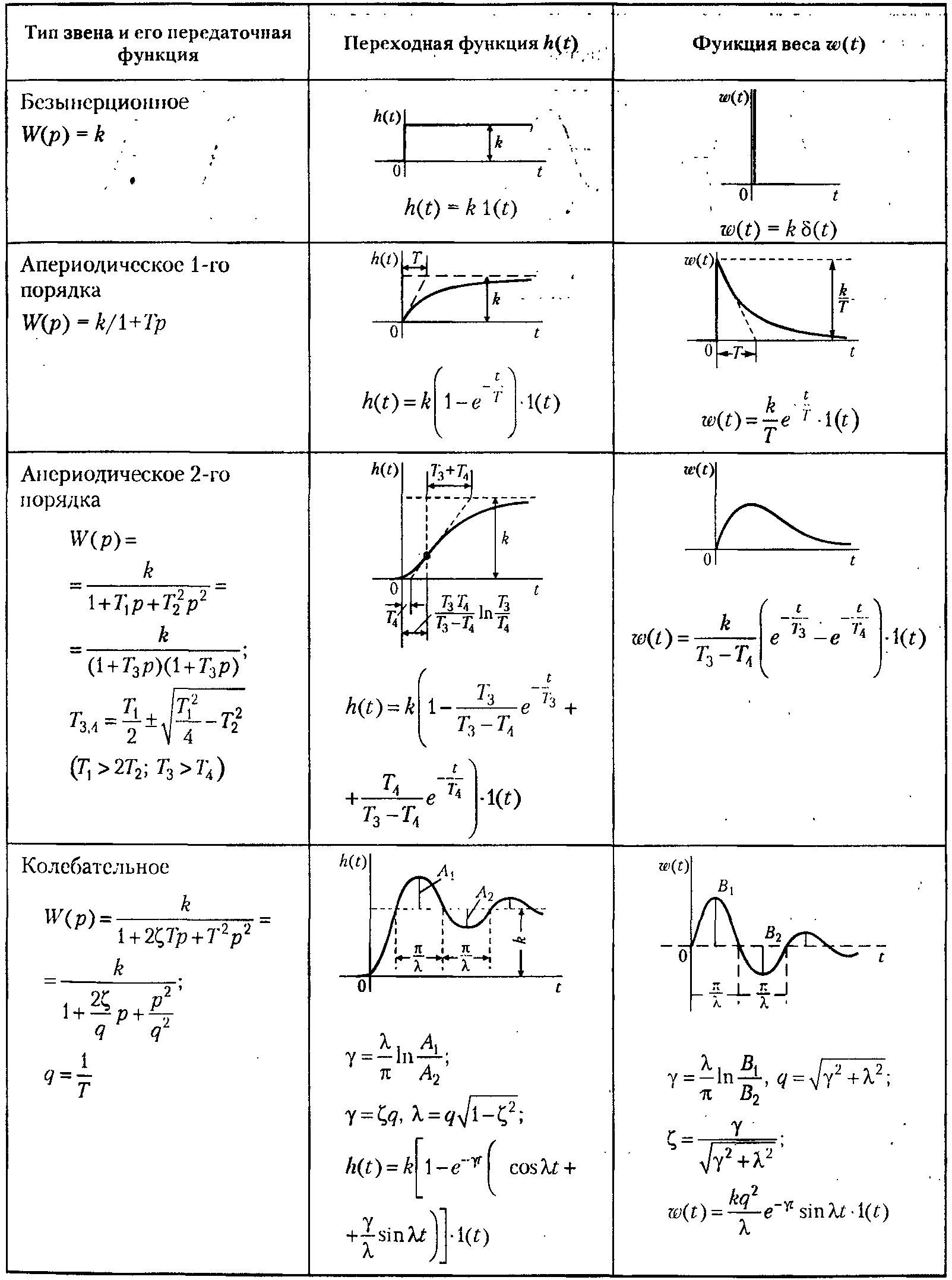 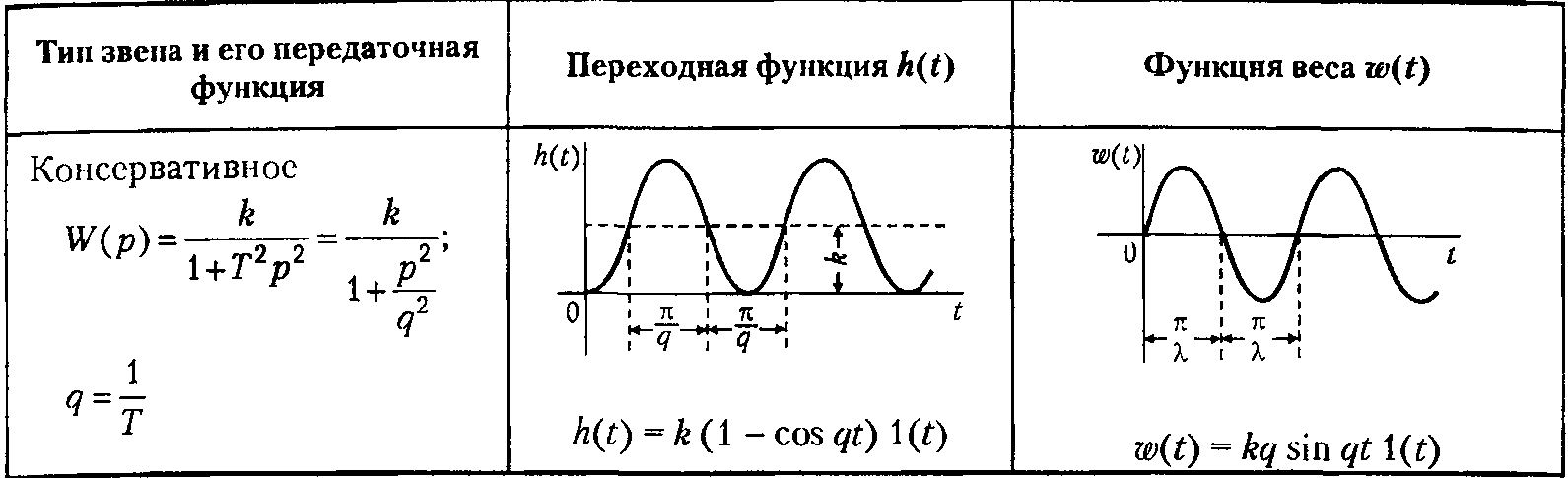 2. Интегрирующие 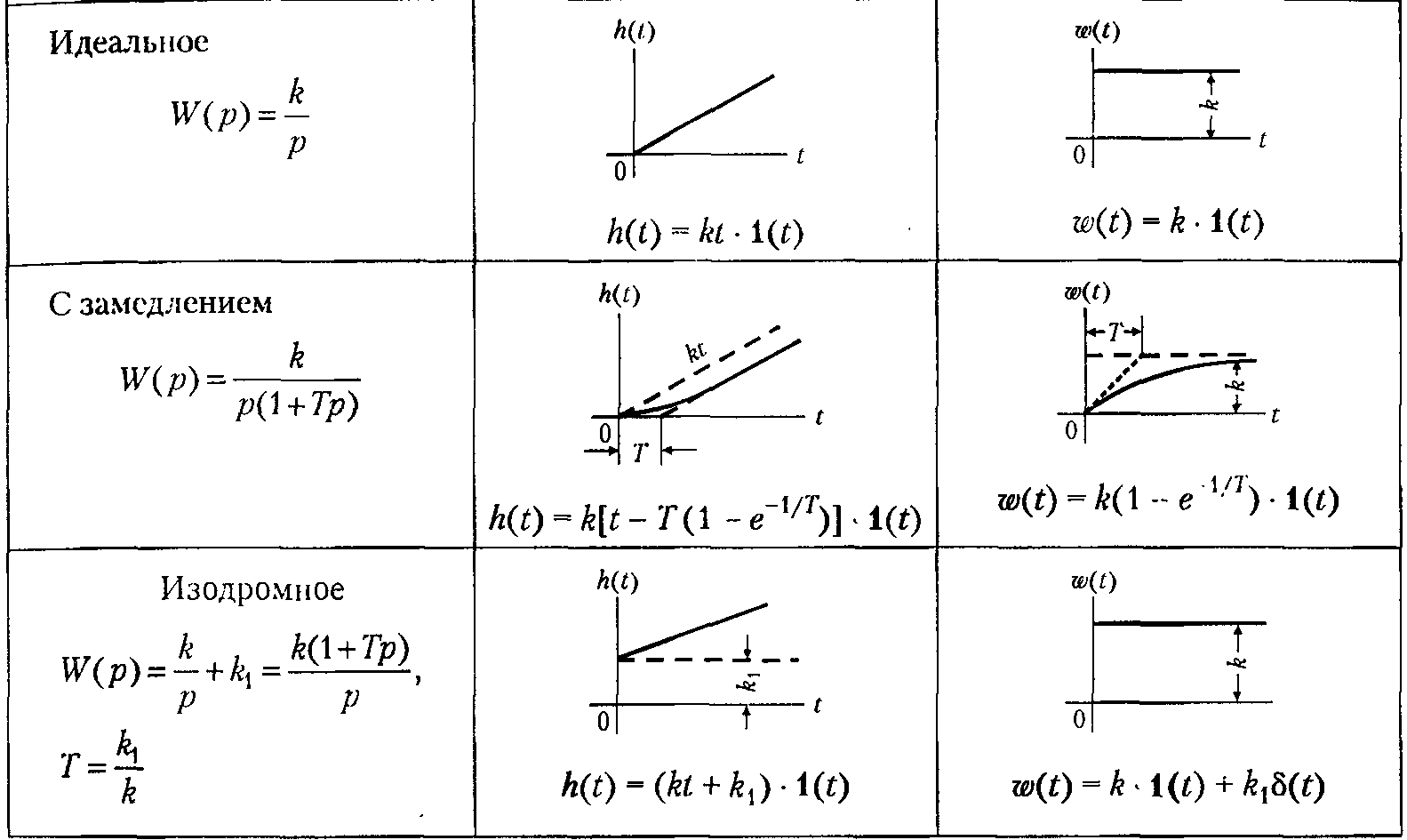 3. Дифферецирующие 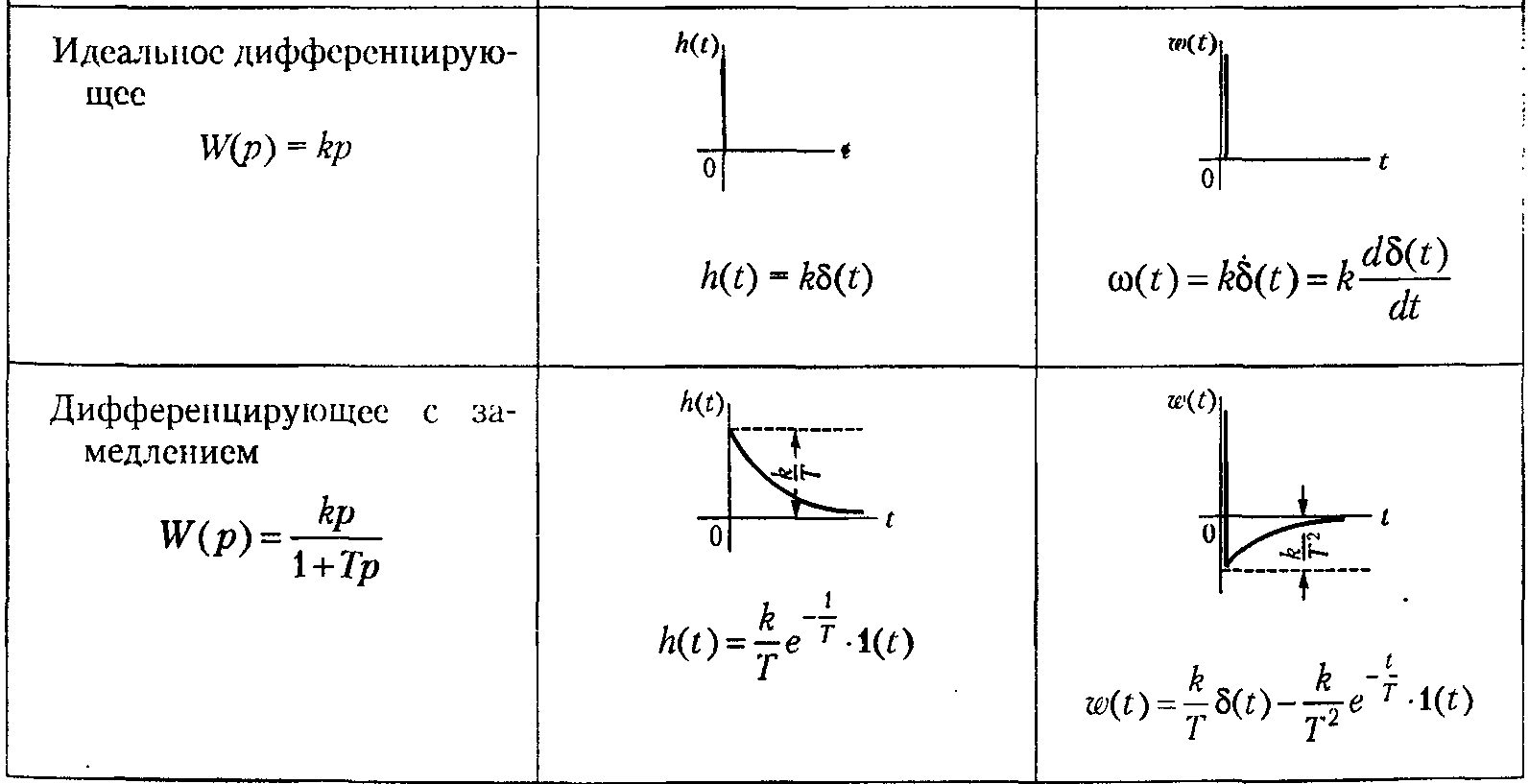 Соединение звеньев.  4. Частотные характеристики Частотная передаточная функция получается из обычной заменой оператора Лапласа s(или р) на комплексную частоту j, т.е. в результате перехода от изображения Лапласа к изображению Фурье. Дифференциальное уравнение движения системы связывает входной и выходной сигналы (т.е. функции времени), передаточная функция связывает изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры. Частотная передаточная функция может быть представлена в следующих видах: W(j) = A() e j(), или W(j) = U() + jV() ; где:
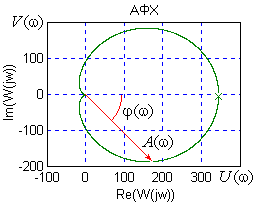
Амплитудно-фазовая характеристика (годограф Найквиста) Это геометрическое место точек, которые описывает конец вектора частотной передаточной функции, при изменении частоты от -∞ до +∞. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка. От АФХ порождаются все другие частотные зависимости:
Логарифмические частотные характеристики. Логарифмические частотные характеристики (ЛЧХ) включают в себя построенные отдельно на одной плоскости логарифмическую амплитудную характеристику (ЛАЧХ) и логарифмическую фазовую характеристику (ЛФЧХ). Построение ЛАЧХ & ЛФЧХ производится по выражениям: L() = 20 lg |W(j)| = 20 lg A(), [дБ]; () = arg(W(j)), [рад]. Величина L() выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один Бел соответствует увеличению мощности в 10 раз, 2 Бела – в 100 раз, 3 Бела – в 1000 раз и т.д. Децибел равен одной десятой части Бела. Примеры АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ для типовых динамических звеньев приведены в таблице 2. Таблица 2. Частотные характеристики типовых динамических звеньев. 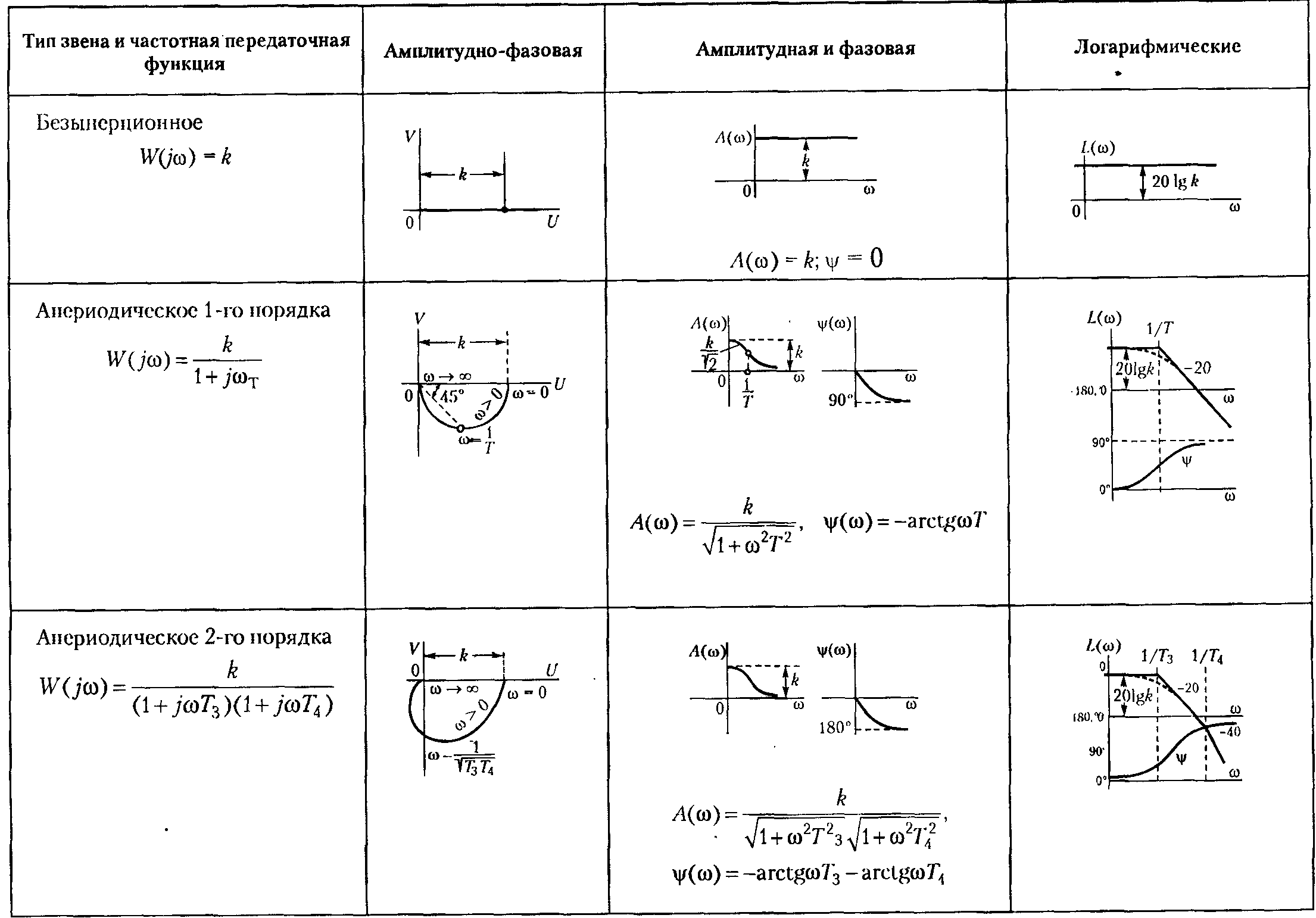 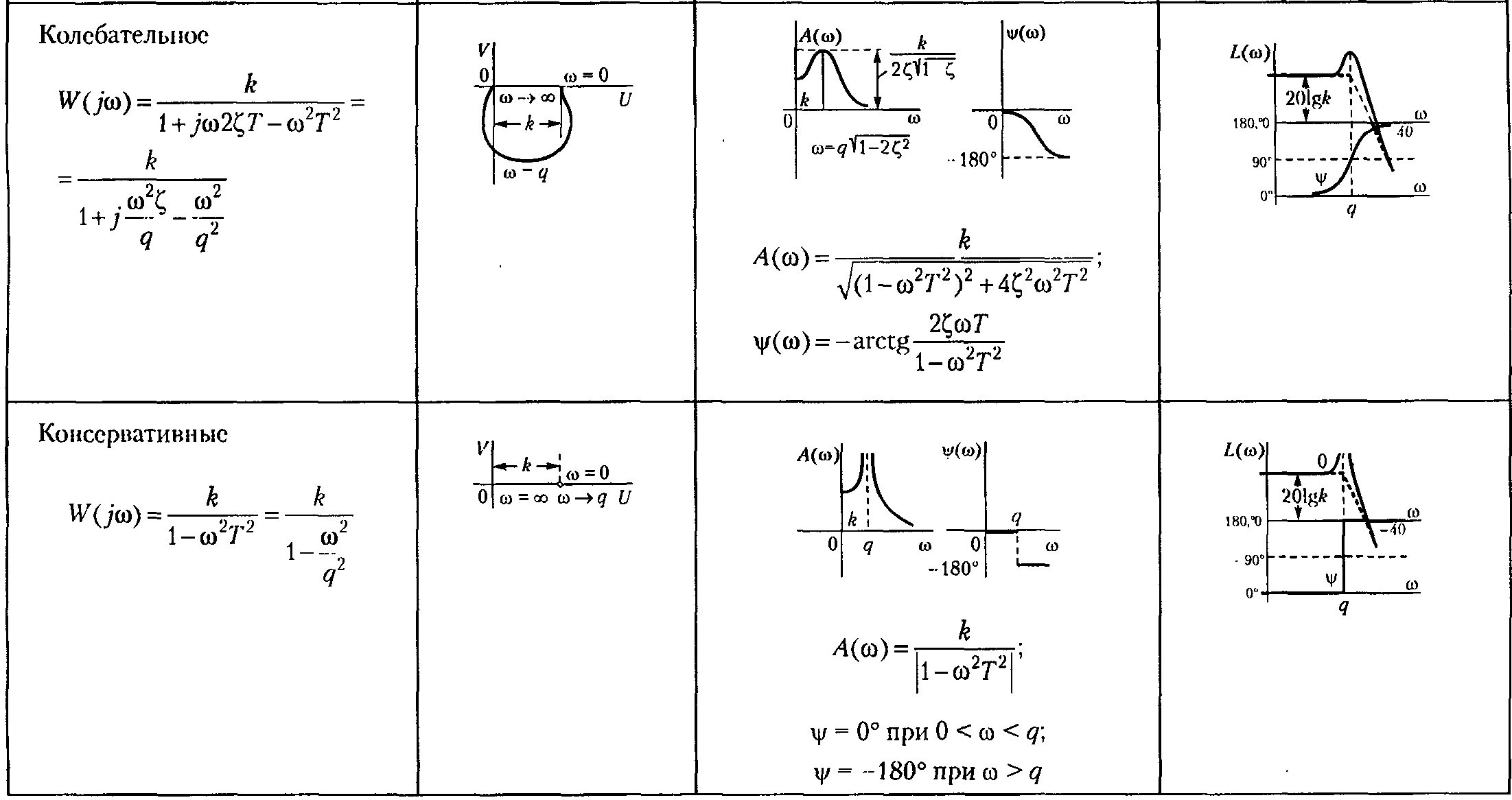 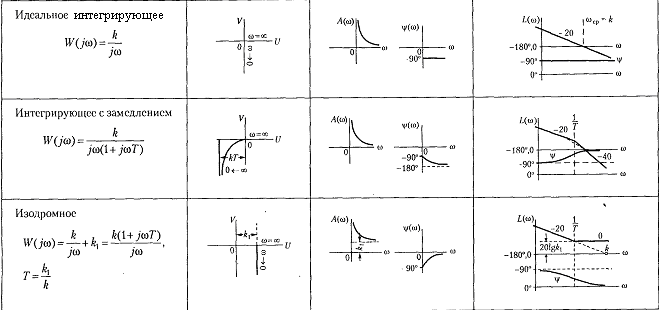 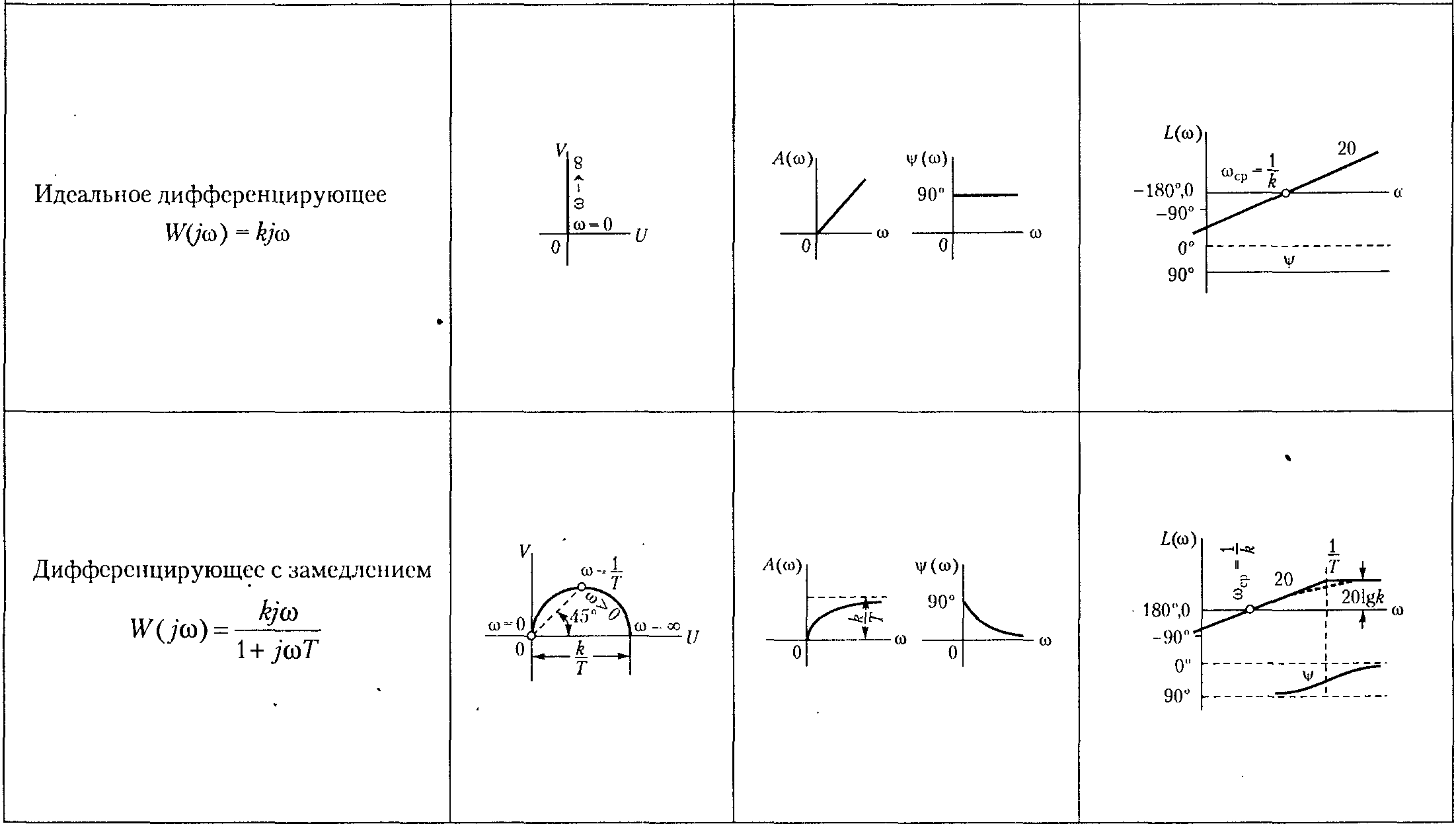 |

 () и V() - вещественная и мнимая части частотной ПФ. Для их нахождения немобходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.
() и V() - вещественная и мнимая части частотной ПФ. Для их нахождения немобходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.